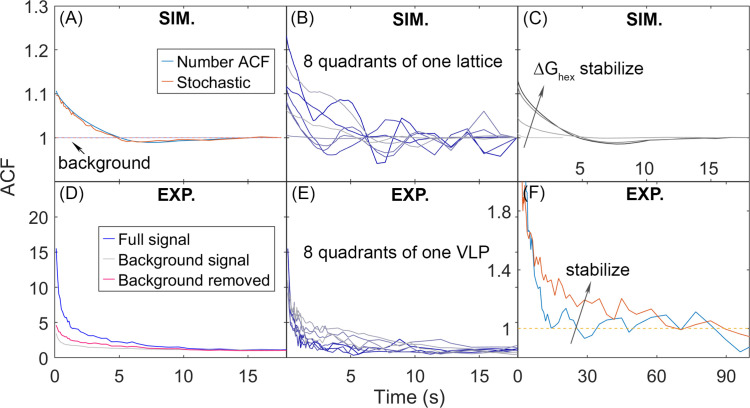
Figure 7. Autocorrelation functions (ACFs) of lattice dynamics from simulation and experiment show qualitatively similar trends.

(A) Number ACF of the simulations calculated directly from the copy numbers of Gag monomers shown in blue line. Averaged over all 8 quadrants over all 60 traces for one parameter set (see Methods). Using the stochastic localization method that mimics experiment shows excellent agreement (orange line). Dashed lines are the background signal, which is 1 as expected (bleaching of the Gag monomers causes limited drops in total copies across 20 s), as the total copy numbers across the membrane surface do not change. We note that the ACF values at our longest delays (i.e. τ>~10 s) are not statistically robust, because of the limited number of frames separated by these timescales. (B) ACF of each of the 8 quadrants of one simulated lattice. (C) As the lattice is stabilized by increasing ΔG_hex, the ACF shows higher amplitude correlations that decay to 1 at longer times, additional trends shown in Figure 7—figure supplement 1. (D) ACF from stochastic localization experiments on Gag virus-like particles (VLPs). The blue curve is the average signal over all 8 quadrants over 11 VLPs. The gray is the background signal for the ACF of the total copy numbers across the surface, then averaged over all VLPs. The red line is the ACF signal after dividing out the background. (E) ACF of 8 quadrants of one experimental VLP. (F) The ACF from VLPs that have been stabilized with a fixative (orange curve) show the same trend as the stabilized lattices from simulation. The y-axis has been zoomed in to demonstrate the shift. The influence of experimental measurement noise on simulated ACFs is shown in Figure 7—figure supplement 2.

Figure 7—figure supplement 1. Autocorrelation functions (ACFs) at different free energies, reaction rates, diffusion, and surface coverage.

(A) The ACF amplitude increases at short times as the hexamer energy stabilizes, as (B) reaction rates slow, as (C) diffusion is faster, as (D) lattice coverage decreases. This is due to increased heterogeneity within the system leading to a larger variance in the copy numbers per quadrant.

Figure 7—figure supplement 2. Effects of introduced noise on the autocorrelation functions (ACFs) calculated from stochastic localization measurements on simulation trajectories.

(A) From simulation we can directly count the number of monomers in each quadrant, and generate the complete number ACF. We can also perform a stochastic localization experiment, to mimic experiment, producing excellent agreement. In each frame, a monomer was localized here with 60% probability, p_act = 0.6. Reducing the probability increases the noisiness of the ACF, but not its amplitude or timescales. No other ‘error’ was introduced into the localization measurement. For all plots, the background signal is shown in dashed red. The background is the correlation of the total copies counted across the full surface (no separation into quadrants). It is 1 as expected for the simulations due to conservation of total copies when no measurement noise is introduced. (B) For the stochastic localization, we add blinking of the fluorophore. Each molecule, once localized, can be localized again within the 10 frames (1s) since its first localization, with maximal three total localizations. Each molecule is on average localized twice, based on the experimental characterization of the Dendra fluorophore (Saha and Saffarian, 2020). (C) Here, we have the probability of localizing a molecule decays with time, p_act = 0.6exp(−t/10), such that early on, more localizations occur than later on in the trajectory. This mimics a distribution of activation times for the fluorophores. (D) Here, we set the surface of the sphere is assumed to be only partially ‘visible’ to the laser. Here, only the top 4 quadrants are detected and analyzed, and the bottom 4 quadrants are ‘dark’. Those monomers in the bottom half become visible once they diffuse into the top hemisphere. (E) Similar to (D), except here the visible part of the sphere is asymmetric. The lattice is shifted to a distance along the x-axis and z-axis and only the molecules whose distance to the origin is less than R_sphere = 67 nm are visible. Monomers outside of that region are ‘dark’, until they diffuse into the visible part of the surface.