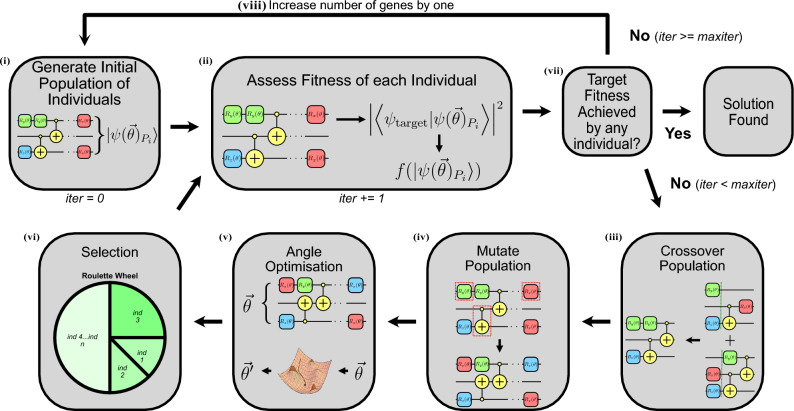
Figure 1.

Overview of the GASP approach, given a desired target state vector $|{\psi }_{\mathrm{target}}⟩$. (i) Then, create initial population $\{P\}$, of individuals, $P_i$, which are each a quantum circuit, that generates the population states $|\psi {(\overrightarrow{\theta })}_P⟩$, with the appropriate number of qubits and number of genes for the given state vector. (ii) Assess the fitness of the state vectors determined by each individual in the population: $f(|\psi {(\overrightarrow{\theta })}_{P_i}⟩)=|⟨{\psi }_{\mathrm{target}}|\psi {(\overrightarrow{\theta })}_{P_i}⟩{|}^2$. (iii) Apply crossover to the population, producing $|\psi {(\overrightarrow{\theta })}_{\mathrm{new}}⟩$. (iv) Mutate the entire population with probability $p=5\%$. (v) Run classical optimisation on each mutated individual to obtain the optimal $\theta$ values between 0 and $2\pi$, to achieve the highest fitness for their generated circuit. (vi) Apply roulette wheel selection to the population, to select the individuals for the next generation based on their assessed fitness. (vii) Repeat until the desired fitness is achieved or maxiter iterations since the last increase in fitness was achieved. (viii) If maxiter iterations since the last increase in fitness, increase the number of genes by 1 and return to (i).