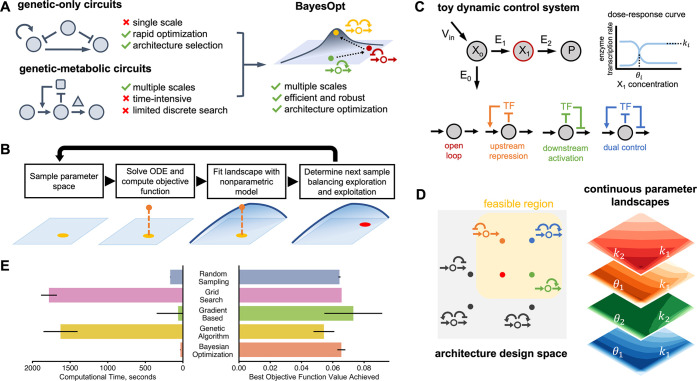
Figure 1.

Bayesian optimization for the design of circuit architectures and parameters. (A) Previous optimization methods have focused on genetic circuits in isolation from other cellular processes. For multiscale circuits, optimization approaches become infeasible due to the difficulty of simulating stiff dynamical systems in many locations of the design space; a common example of such multiscale systems are gene circuits that control metabolic production.³ We propose the use of Bayesian optimization (BayesOpt) for efficient optimization of architectures and parameters in multiscale circuits. (B) Schematic of a mixed-integer Bayesian optimization loop; the objective function is regarded a random variable to be optimized over an input space comprised of continuous parameters and a set of discrete circuit architectures. At each iteration, the algorithm computes the value of the objective function from the solution of an ordinary differential equation (ODE) model at a single location in the input space. The algorithm learns the shape of the objective landscape using a nonparametric statistical model,³⁷ which is employed to propose a new location in the input space through an acquisition function designed to balance exploration and exploitation of the input space; more details in the Methods. The algorithm iteratively learns the shape of the performance landscape until convergence to a global optimum. (C) Example metabolic pathway under gene regulation. We consider three negative feedback architectures plus open loop control; the architectures are named based on the net effect of the metabolite on gene expression. The intermediate X₁ binds a transcription factor (TF) that controls the expression of pathway enzymes, either as an activator or repressor. V_in is the constant influx to the engineered pathway from native metabolism. The TF dose-response curve (at right) is described by three parameters, k_i, θ_i, and n_i, where i = 1, 2. The aim is to find designs with optimal architecture and dose-response parameters (k_i, θ_i); for simplicity the Hill coefficient was fixed to n_i = 2. (D) Performance landscapes of the four feasible circuit architectures. We exclude architectures with positive feedback loops as these are prone to multistability.⁴⁷ The shape of the performance landscape defined in eq 3 shows substantial variation across the four architectures. This leads to a highly nonconvex mixed-integer optimization problem. Heatmaps show the value of the objective J computed on a regular grid of the indicated parameters. (E) Comparison of BayesOpt against other strategies using the toy model as a benchmark; lower objective function values are better. Shown are the results for random sampling (N = 1,000 samples), grid search (N = 40,000), a genetic algorithm⁵⁵ (N = 100 individuals, N = 1,000 generations), and a gradient-based optimizer to find optimal continuous parameter values for each architecture.⁴⁸