Figure 4.

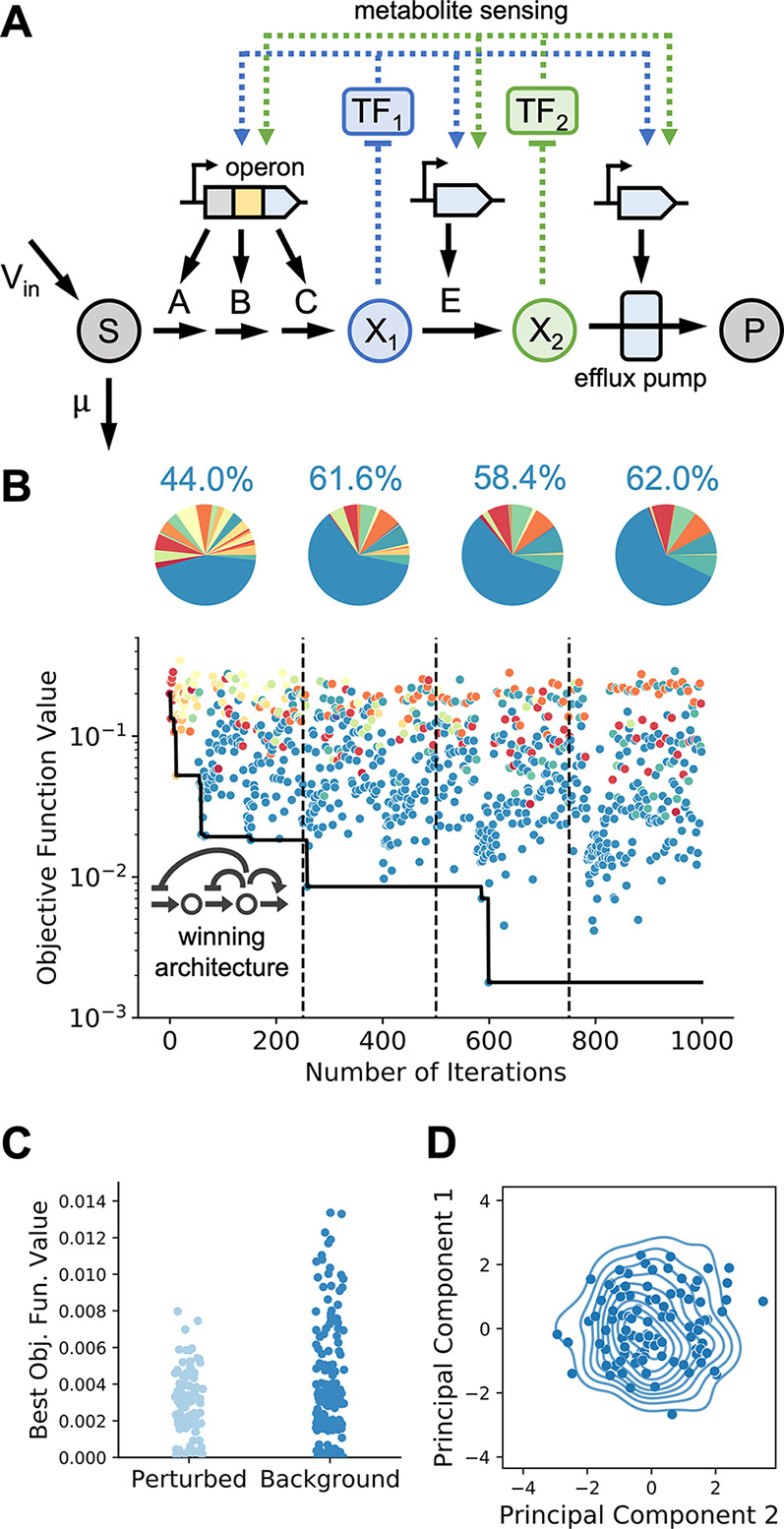
Bayesian optimization in a complex pathway. (A) Schematic of pathway for production of p-aminostyrene.³⁴ Two intermediates can act as ligands for metabolite-dependent riboregulators, and three promoter sites of control. The optimization problem has 16 continuous decision variables and 27 circuit architectures. The substrate S is converted by enzymes A, B, and C to X₁, which is then converted by E to X₂. The toxic substrate X₂ is then pumped out of the cell via an efflux pump to form the product P. Both X₁ and X₂ can act on the transcription factors TF₁ and TF₂. V_in is the constant influx to the engineered pathway from native metabolism. (B) Representative run of the BayesOpt algorithm; the method samples many architectures before settling on the optimal one. Pie charts show continued exploration of a large number of architectures. The winning architecture is shown in the inset. (C) The p-aminostyrene pathway has several forms of substrate, protein, and enzyme toxicity expressed via a toxicity factor τ (see eq 6). To explore the effects of protein and metabolite toxicity, we perturbed the toxicity factor. Metabolite-induced toxicity was perturbed on the nominal range (1 × 10^–3, 1 × 10^–4) and protein-induced toxicity on the range (1 × 10^–4, 1 × 10¹) respectively. Both ranges were selected to match the ranges provided in the literature.³⁴ Latin Hypercube sampling was used to generate N = 100 perturbed parameter values, and the optimal solutions were compared to an equal number of background solutions using the nominal parameter values. (D) Visualization of the optimal solutions; scatter plot of principal components of the optimal parameter values for the model with perturbed toxicity parameters (N = 100). Contour plots show the background distribution of parameter values.