Abstract
Understanding how the highly unstable carbocation intermediates in terpenoid biosynthesis are stabilized and protected during their transient existence in enzyme active sites is an intriguing challenge which has to be addressed computationally. Our efforts have focused on evaluating the stabilization afforded via carbocation-π complexation between a biochemical carbocation and an aromatic amino acid residue. This has involved making measurements on an X-ray structure of an enzyme active site that shows a π donor proximate to a putative carbocation site and using these to build models which are analyzed computationally to provide an estimated stabilization energy (SE). Previously, we reported estimated SEs for several such carbocation-π complexes involving phenylalanine. Herein, we report the first such estimate involving tryptophan as the π donor. Because there was almost no published information about indole as a π-complexation donor, we first located computationally equilibrium π and σ complexes of 3-ethylindole with the t-butyl cation as relevant background information. Then, measurements on the X-ray structure of the enzyme CotB2 complexed with geranylgeranyl thiodiphosphate (GGSPP), specifically on the geometric relationship of the putative carbocation at C15 of GGSPP to W186, were used to build a model that afforded a computed SE of −15.3 kcal/mol.
Introduction
Carbocations are crucial intermediates in the biosynthesis of terpenes and steroids,1 and understanding how these highly unstable species can be stabilized during biochemical reactions and protected from unwanted combination with active site nucleophiles is an intriguing scientific challenge. Cation-π interaction2,3 between positively charged metal and ammonium ions and aromatic amino acid side residues is well recognized as an important contributor to binding in proteins. Experimental studies have provided quantitative evidence concerning such interactions,4,5 and computational analyses6 have provided further quantitative data concerning the cation-π interactions of these types of cations. But for carbocations, which exist only fleetingly during enzyme-catalyzed reactions, it has not been possible to obtain similar quantitative experimental information about their cation-π interactions. A number of X-ray structural studies of enzymes that catalyze formation of polyisoprenoid natural products show aromatic amino acids in positions, suggesting roles in stabilizing carbocation intermediates.1 In addition, site-directed mutagenesis experiments have provided evidence that carbocation-π interactions do indeed play a role in the mechanisms of terpene cyclases.7−9
Jenson and Jorgensen10 provided early theoretical work on interactions of carbocations putatively intermediate in steroid biosynthesis with models for aromatic amino acids. Further valuable insights into the carbocationic mechanisms involved in the biosynthesis of steroids and related triterpenoids have been provided by Hess and co-workers.11−14 Tantillo and co-workers15−19 have conducted extensive computational investigations of the numerous complex rearrangements of carbocation intermediates in terpenoid biochemistry. In particular, Hong and Tantillo17,18 have elucidated the important roles that intermolecular C–H−π interactions may play in the biosynthesis of complex terpene natural products using benzene to represent the aromatic residues often found in the active sites of terpene synthases. Tantillo19 has reviewed critically the several computational methods used to study the complex carbocation rearrangements found in the mechanisms of terpenoid cyclases. In a similar vein, Major and co-workers20 have presented a study of quantum mechanics-molecular mechanics methods (QM/MM) for carbocation chemistry. Sato et al.21,22 have reported theoretical and experimental studies of carbocation rearrangements that occur in the biosynthesis of the terpenoids cyclooctatin and sesterfisherol.
During the last decade, there have been extensive studies on the mechanism of the terpenoid cyclase reaction catalyzed by the enzyme CotB2. These have been reported by investigators including Hong and Tantillo,17 Tomita et al.,23 Tang et al.,24 and Major and co-workers.25−28 All these investigators have included computed energy profiles for at least major portions of the multistep enzymatic reaction. The report by Tomita et al.23 includes an X-ray structure of CotB2 with an unreactive substrate in the active site which has provided the essential measurements for the work described in this manuscript. The extensive calculated energy profiles reported by Major and co-workers28 have also been a source of important relevant information.
Our previous efforts concerning carbocation-π interaction have included a computational study of the complexation of the methyl cation with benzene,29 which provided support for the idea that carbocation-π interaction should be stronger for both η2 and η1 complexes over the periphery of an aromatic system, as opposed to the cation-π interactions of ammonium and metal ions, which form η6 complexes with aromatic rings.4 We have also described a computational study of the carbocation-π interaction of the 1,1-dimethylallyl cation (DMA+) with benzene30 in which a complex of benzene bound to both ends of the DMA+ π system was located on the potential energy surface. This complex was found to be more stable than the related σ complex, possibly affording insight into why biological reactions involving this type of carbocation do not lead to electrophilic substitution of aromatic rings present in protein active sites. More recently, we have adopted a new strategy, in which X-ray structures of enzyme active sites binding a carbocation surrogate are used as a basis for analysis.31,32 This approach has the distinct advantage that the calculated stabilization energies are based on experimental measurements of the relative positions of the aromatic amino acid and the putative carbocation in the active site. This approach, using measurements of this geometric relationship in X-ray structures, presumably can give a more realistic approximation of the actual geometry that evolved to produce an effective active site than is afforded by alternate approaches used to study carbocation-π interactions. However, because X-ray structures do not directly show the positions of hydrogen atoms, such structures alone do not allow direct measurement of distances from hydrogen atoms to other atoms. Later, in this manuscript, we explain how our approach addresses this limitation allowing us to assess the relative contribution of C–H−π interactions.
In our initial study of this type, we reported31 the first quantitative evaluation of the stabilization energy that a phenylalanine can provide to a biochemical carbocationic intermediate via π complexation. This was accomplished by an analysis of the X-ray structure, reported by Köksal et al.,33 of geranyl diphosphate C-methyl transferase (GPPMT) bound to the modified, unreactive substrate S-thiolodiphosphate (GSPP), which had been employed in place of the natural substrate geranyl diphosphate (GPP) in the reaction catalyzed by GPPMT, as shown in Figure 1a,b. Phenylalanine 222 in GPPMT is “ideally positioned”33 to afford stabilization via carbocation-π interaction with the intermediate carbocation 2MGSPPH+ that would be formed from GSPP. We constructed a complex model (Model 1, Figure 1c) of the active site of GPPMT bound to 2MGSPPH+, calculated its energy, and compared it to the sum of the energies of the component parts of this model, affording an estimated carbocation-π binding energy of −12.4 kcal/mol.31 A key feature of this study, of course, was that the X-ray structure provided an excellent estimate of the position of phenylalanine F222 relative to that of the carbocation 2MGSPPH+. As previously described,31 building this complex model, including conducting the geometrical optimizations required to refine its structure, was a lengthy, computationally demanding process.
Figure 1.
(a) Reaction catalyzed by GPPMT with GPP to form 2-methylgeranyldiphosphate (2MGPP) via intermediate carbocation 2MGPPH+. (b) Also shown is unreactive substrate analogue GSPP, which also binds in the active site of GPPMT, and 2MGSPPH+, the putative carbocation that would be formed by C2 methylation of GSPP. (c) Model 1, constructed by aligning the t-butyl cation with ethylbenzene having the side-chain dihedral angle (∠C6–C1–C7–C8) constrained to the value of the corresponding angle in F222 of GPPMT determined from measurements made on the X-ray structure of the active site of GPPMT bound to GSPP.33 The numbers representing distance measurements are in Å units. The content of this figure is an adaptation of information presented in Figures 1 and 4 of ref (32).
In previous work,31 we had found an equilibrium complex of ethylbenzene with the t-butyl cation that had a geometrical relationship of the binding partners very similar to that of F222 with GSPP in the X-ray structure.33 This led us to consider the possibility that evaluating the interaction of a simple cation such as the t-butyl cation with an appropriate ethylbenzene (as a surrogate for phenylalanine) in a geometrical relationship closely approximating that in an X-ray structure might be a convenient method to reliably estimate tertiary carbocation-π interactions. To this end, the distances, angles, and dihedral angles that define the geometric relationship between F222 and C3 of GSPP bound to GPPMT in the X-ray structure33 were used to construct model 1 (Figure 1c) of the t-butyl cation with ethylbenzene that corresponded as closely as possible to these measurements. Complex 1 was optimized with the dihedral angle ∠C6–C1–C7–C8 constrained to the value determined from the X-ray structure33 and its calculated energy compared to the sum of the energies of the optimized isolated binding partners to provide a value of −12.3 kcal/mol as the stabilization that F222 could afford to 2MGSPPH+,32 essentially identical to the value of −12.4 kcal/mol obtained with the complex model.31 This result confirmed that use of this simple model did indeed provide a reliable estimate of the stabilization that F222 could afford to 2MGSPPH+. The calculations used to estimate the stabilization energy for model 1 required less than 3% of the computer time required for the analogous calculations with the original more complex model.
Explorations of the effect of modifying the rotation of the t-butyl group relative to that of the ethylbenzene and the effect of the small geometrical changes in the structure of the optimized t-butyl cation necessary to reflect more closely the carbocationic site in the active site structure led to calculated binding energies that vary by no more than 0.3 kcal/mol from the value of −12.3 kcal/mol determined with model 1.32 Thus, this second, relatively simple approach, provides a rapid and convenient way to explore X-ray structures which show aromatic amino acid residues positioned to interact with incipient tertiary carbocations.
We next tested this new method with an example of the other common type of carbocation formed in enzyme active sites during terpenoid biosynthesis, the 1,1-dialkylallyl cations formed by ionization of various isoprenoid diphosphates. The X-ray structure of aristolochene synthase bound to the modified substrate farnesyl-S-thiolodiphosphate (FSPP), reported by Chen et al.,34 offered the possibility of examining the interaction of two phenylalanines (F81 and F147) with the farnesyl cation (F+) that would be formed by ionization of FSPP (or FPP). Initially, we built an active site model analogous to model 1 (Figure 1c) using the coordinates in the X-ray structure34 to create a model showing F+ and proximate portions of the active site. Then, phenylalanines F81 and F147 were converted to the appropriate corresponding ethylbenzenes. FSPP was removed and replaced by an appropriately modified DMA+, which was positioned so as to have geometrical relationships with the ethylbenzene surrogates for F81 and F147 that were as similar as possible to those determined from the X-ray structure. The resulting model 2 is shown in Figure 2. Appropriate calculations on model 2 and its component parts afforded a stabilization energy of −10.3 kcal/mol.32 This recent report also described32 application of this method to the analysis of an X-ray structure of the same enzyme active site bound instead to an ammonium ion inhibitor as carbocation surrogate.34 We also reported32 estimates of stabilization energies provided by each of four phenylalanines to each of four putative carbocation intermediates in the formation of lanosterol from squalene oxide by similar analysis of an X-ray structure of that product bound in the active site of oxidosqualene cyclase.35
Figure 2.

Model 2, comprising two ethylbenzenes representing phenylalanines F81 and F147 in positions relative to an appropriately modified DMA+ that approximate the relative positions of F81, F147, and FSPP in the X-ray structure.34 The numbers representing distance measurements are in Å units. The content of this figure is taken from Figure 7 in ref (32).
In the present work, we have turned attention to the application of our simple method to carbocation-π complexation involving interaction of a second type of aromatic amino acid, tryptophan, as the π donor to a biochemical carbocation intermediate. This investigation includes a study of complexation of indole and 3-ethylindole (chosen as an appropriate surrogate for tryptophan) with the t-butyl cation that provided relevant background information for the evaluation of the stabilization energy in a complex of a tryptophan with a tertiary biochemical carbocation. This work also revealed, in the active site X-ray structure being studied,23 certain geometric relationships that afforded additional insight into the mechanism of the reactions occurring at the site of the carbocation-π interaction under consideration.
Results and Discussion
Before beginning a search for an X-ray structure having a tertiary carbocation surrogate bound to tryptophan in the active site, we thought it important to conduct a general study of indole as a complexing partner with the t-butyl cation, our surrogate for biochemical tertiary carbocations. In their pioneering 1997 study of carbocations relevant to steroid biosynthesis, Jenson and Jorgensen10 described a complex of indole with the t-butyl cation, optimized at the B3LYP/6-31G* level, which had the positively charged carbon 3.61 Å from C3a and 3.81 Å from C7a of indole, with an energy of −15.3 kcal/mol relative to the energies of the binding partners. This is apparently the only previously available information concerning carbocation complexes of indole. Because each of the nine carbon atoms of indole is unique, we believed that a thorough study of carbocation complexation, involving each of the carbons of this heterocycle, was essential if we were going to be adequately prepared to analyze the interaction of any indole carbon atom of tryptophan with a biochemical carbocation.
Complexes of Indole and 3-Ethylindole with the t-Butyl Cation
We searched computationally, at the M06/cc-pVTZ level,36,37 for stationary points on the potential energy surface of the t-butyl cation complexed with indole, concentrating on regions adjacent to and above the periphery of the rings. Of particular interest was the same C3a–C7a region of indole, in order to determine if we would obtain results similar to those of Jenson and Jorgensen.10 In fact, two equilibrium π complexes were found in this region defining the border between the benzene ring and the pyrrole ring of indole, one (π3a) with a C+ to C3a separation of 3.19 Å and the other (π7a) with a C+ to C7a separation of 3.14 Å. These complexes, shown in Figure 3 as 3 and 4, respectively, had energies of −22.0 and −21.0 kcal/mol relative to the sum of the energies of the optimized isolated t-butyl cation and indole. We were able to locate additional equilibrium π complexes only at C4 (π4) and C7 (π7). We also found equilibrium σ complexes with all non-hydrogen atoms and transition state π complexes between several pairs of adjacent equilibrium structures, including those between π3a and π7a, σ2 and σ3, π4 and σ5, σ5 and σ6, and π7 and σ6. Structural details for the π3a and π7a equilibrium complexes are presented in the Supporting Information.
Figure 3.

M06/cc-pVTZ-optimized structures and binding energies (kcal/mol) for π complexes of the t-butyl cation with indole at C3a (3) and C7a (4). The numbers representing distances are in Å units. The numbers in magenta indicate the numbering system for the ring atoms of indole.
The largest binding energy we have calculated for an optimized indole–t-butyl cation equilibrium π complex is −22.0 kcal/mol for 3, whereas that for a benzene–t-butyl cation equilibrium π complex, with a C+–Cring distance of 3.06 Å, at the same level is −13.6 kcal/mol.38 This difference in binding energy probably results from at least two factors. First, the π-electron-donating ability of indole is greater than that of benzene, which is confirmed by an analysis of the occupancies of the valence π-type natural atomic orbitals (NAO).39 The net π donation for complex 3 is calculated to be 0.177, whereas it is 0.111 for the t-butyl–benzene π complex.40 Second, the depictions of the two π complexes in Figure 3 show that they both have geometries permitting C–H−π interactions of hydrogens on two methyl groups of the t-butyl cation, one with the pyrrole ring and the other with the benzene ring of indole. Thus, the C–H−π contributions to the binding energies for the indole π complexes 3 and 4 will be larger than the contribution for the π complex with benzene, which can only form a significant C–H−π interaction with one hydrogen atom of one methyl group of the t-butyl cation. This important capacity to form C–H−π interactions utilizing both rings of indole and two methyl groups of the t-butyl cation is evident in several of the additional π complexes discussed in this paper.
More directly related to our goal of evaluating carbocation-π stabilization by tryptophan was the comparable study we next conducted of complexation of the t-butyl cation with 3-ethylindole, which was chosen as a surrogate for tryptophan. Optimized equilibrium π complexes at C3a (5) and C7a (6) (Figure 4) were found to be very similar to those of the t-butyl cation with indole, having binding energies of −23.2 and −22.6 kcal/mol, respectively. The presence of the 3-ethyl group in 5 and 6 enhances the binding energy in these complexes by 1.2 and 1.6 kcal/mol, respectively.41 The transition state (7) (Figure 4) connecting complexes 5 and 6 was also located and found to have a binding energy of −21.3 kcal/mol. We also discovered equilibrium π complexes involving C4 (8) and C7 (9) (Figure 5), but as was the case for indole, no other equilibrium π complexes were found. On the other hand, equilibrium σ complexes were readily found at every ring structure atom and those with 3-ethylindole bound to C4 (10) and C3a (11) are shown in Figure 6. The C3a σ complex 11 was chosen for illustration because its formation obviously destroys the aromaticity of the indole system, resulting in a nonplanar structure with a drastically reduced binding energy of −16.8 kcal/mol compared to that of the C4 σ complex 10 of −33.0 kcal/mol. Binding energies for equilibrium complexes of both types and for the transition state between the π3a and π7a complexes calculated at the MO6/cc-pVTZ level36,37 and also at the CCSD(T)/cc-pVTZ level37,42 are listed in Table 1.
Figure 4.

M06/cc-pVTZ-optimized structures and binding energies (kcal/mol) for complexes of the t-butyl cation with 3-ethylindole: π at C3a (5) and C7a (6) and the transition state connecting them. The numbers representing distance measurements are in Å units. The numbers in magenta indicate the numbering system for the non-hydrogen atoms of 3-ethylindole and for the C+ atom of the t-butyl cation. The C15 numbering of the central carbon atom of the t-butyl cation is used to emphasize the correspondence to the putative carbocationic site of W186 in the X-ray structure23 discussed later in this manuscript.
Figure 5.

M06/cc-pVTZ-optimized structures and binding energies (kcal/mol) for complexes of the t-butyl cation with 3-ethylindole: π at C4 (8) and C7 (9). The numbers representing distance measurements are in Å units.
Figure 6.

M06/cc-pVTZ-optimized structures and binding energies (kcal/mol) for complexes of the t-butyl cation with 3-ethylindole: σ at C4 (10) and C3a (11). The numbers representing distance measurements are in Å units.
Table 1. Binding Energies (kcal/mol) Calculated at the M06/cc-pVTZ and CCSD(T)/cc-pVTZ Levels for σ and π Complexes of the t-Butyl Cation with 3-Ethylindole and for the π3a → π7a Transition State43.
| molecule | M06/cc–pVTZ binding energy (kcal/mol)a | CCSD(T)/cc–pVTZ binding energy (kcal/mol)b |
|---|---|---|
| σ-complex 1 | –36.87 | –48.87 |
| σ-complex 2 | –45.52 | –52.92 |
| σ-complex 3 | –41.50 | –52.58 |
| π-complex 3a | –23.23 | –23.87 |
| σ-complex 3a | –16.79 | –27.03 |
| π-complex 4 | –22.84 | –23.17 |
| σ-complex 4 | –33.03 | –40.43 |
| σ-complex 5 | –35.62 | –43.96 |
| σ-complex 6 | –35.66 | –43.02 |
| π-complex 7 | –21.35 | –22.46 |
| σ-complex 7 | –33.12 | –41.60 |
| π-complex 7a | –22.59 | –23.62 |
| σ-complex 7a | –20.24 | –31.48 |
| π3a → π7a T.S. | –21.32 | –22.20 |
M06/cc-pVTZ binding energies are calculated using geometries optimized at the M06/cc-pVTZ level with all stationary points confirmed by harmonic frequency calculations.
CCSD(T)/cc-pVTZ energies calculated at the M06/cc-pVTZ-optimized geometries.
For the four π complexes, calculated NBO39 M06/cc-pVTZ charges on the C+ center are almost identical: 0.550 for π3a, 0.551 for π4, 0.550 for π7, and 0.541 for π7a. However, despite the equilibrium C+–Cring distance varying from 3.24 Å in π3a (5) to 2.78 Å in π7 (9), the binding energies for all four equilibrium π complexes are remarkably similar.44 Based solely on the carbocation C+ -- π interaction, complex π3a (5), with the largest C+–Cring distance (3.24 Å), might be expected to have the weakest binding. But, as shown in Figure 4, the C–H−π stabilization in complex π3a is enhanced because it arises from significant interactions with both the benzene and the pyrrole rings. In contrast, complex π4 (8) (Figure 5) has a shorter C+–Cring distance of 2.84 Å, suggesting a stronger C+ -- π system interaction than for π3a, but it has a weaker contribution from C–H−π stabilization, which is significant only with the benzene ring. These off-setting contributions lead to binding energies for π complexes 3a (5) and 7a (6) that are very similar to those for π complexes 4 (8) and 7 (9).
As shown in Table 1, the calculated binding energies of the π complexes are closely similar at the two computational levels, but those of the σ complexes differ markedly. This same disparity was previously found in our study of the complexation of ethylbenzene with the t-butyl cation.31 In that case, the calculated binding energies for the π complexes were very similar, −16.3 kcal/mol at the M06 level36 compared to −16.8 kcal/mol using the CCSD(T) method,42 whereas the binding energies for the σ complexes were quite different, −10.4 kcal/mol at M06 vs −15.9 kcal/mol at CCSD(T). One possible source of this discrepancy might be that the CCSD(T) energy calculations were performed for geometries optimized using the M06 approach. To explore this possibility, geometries of the π and σ t-butyl cation–ethylbenzene complexes were optimized at the CCSD(T)/cc-pVTZ level.37,42 These optimized structures are found to be in excellent agreement with those calculated using the M06 method.45 Moreover, M06 binding energies calculated for the t-butyl cation–ethylbenzene complexes with structures optimized at the CCSD(T)/cc-pVTZ level agree very closely with CCSD(T) results obtained with the M06-optimized geometries: −16.7 kcal/mol vs −16.8 kcal/mol for the π complex and −15.6 kcal/mol vs −15.9 kcal/mol for the σ complex. These results suggest that the M06/cc-pVTZ method provides accurate structures for both π and σ complexes in such carbocation-π complex systems and gives calculated π complex binding energies that agree very closely with those obtained at the CCSD(T) level. Although the reason for the disparity between the binding energies calculated by the two methods for σ complexes remains unclear,46 these findings provide strong support for use of the M06/cc-pVTZ method for studying π stabilization energies for a carbocation with a tryptophan residue.
Evaluation of Carbocation-π Stabilization Energy Afforded by Tryptophan
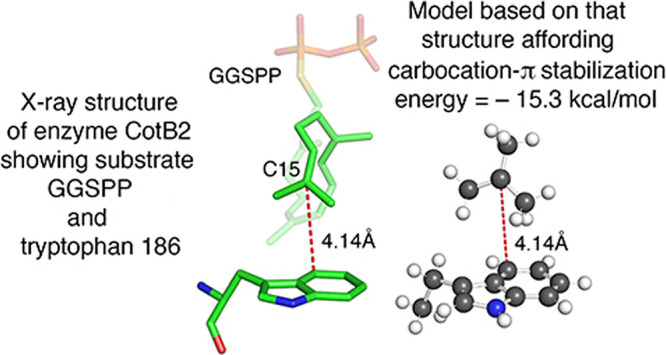
With these results in hand, we searched for literature reports that included active site X-ray structures showing carbocation surrogates located proximate to a tryptophan residue so that we could apply our knowledge of 3-ethylindole complexation as a guide to construction of appropriate model structures for calculation of π stabilization energies for that amino acid residue. As there were for phenylalanine,47,48 there are numerous examples of X-ray structures depicting possible carbocation-π interaction between tryptophan and a carbocation surrogate.23,47−49 We located and examined the X-ray structures in almost all of these referenced papers, looking not only for a clear and promising geometric relationship between the tryptophan residue and the bound unreactive substrate surrogate but also for a substrate that was structurally similar at the putative carbocationic site. For example, a substrate having the same trigonal hybridization at the site of the positively charged carbon as in the natural substrate should be a better surrogate for our purposes than one with tetrahedral hybridization at that site. This correspondence of trigonal hybridization was the case in our initial estimate of the stabilization energy afforded to a biochemical carbocation by phenylalianine,31 as depicted in Figure 1. Among the papers examined, the report by Tomita et al.,23 mentioned in the Introduction, seemed particularly promising. This article concerning the CotB2-catalyzed cyclization of GGPP to cyclooctat-9-en-7-ol is partially summarized in Figure 7. This paper presents an X-ray structure with the unreactive, modified substrate geranylgeranyl thiodiphosphate (GGSPP), which meets the trigonal hybridization criterion, bound in the active site with C15 of GGSPP clearly positioned to interact with W186 of CotB2, as shown in Figure 8.23 The closest carbon atom of W186 to the putative carbocation at C15 is C4 of W186 at a distance of 4.14 Å, with the angle ∠C7–C4–C15 that relates 3-ethylindole to GGSPP at 97.5°. The substantial binding energy of the 3-ethylindole -- t-butyl cation π complex at C4 (Table 1) is consistent with C15 of W186 participating in this carbocation-π interaction. Both Tomita et al.23 and Raz et al.28 have previously noted that W186 is possibly positioned to provide stabilization to the C15 carbocation in the CotB2-catalyzed reaction. However, they do not discuss or provide any estimate of the carbocation-π stabilization afforded by W186 to the carbocation at C15. Also, the distances they report are from the C15 carbocationic center to an undefined centroid of the indole ring of W186. As noted in the Introduction, we have provided evidence29 that carbocation-π interaction is stronger over the periphery of an aromatic ring (η1 or η2 bonding) as opposed to bonding over the center of the ring (η6 bonding for benzene). Further examination of the X-ray structure of GGSPP in the active site of CotB2 provided further measurements of the area surrounding C15 that afforded additional insight into the mechanism of the formation and subsequent reaction of the putative C15 carbocation. This aspect will be briefly discussed before the details of our analysis of the C15+ -- W186 interaction are presented.
Figure 7.

Abbreviated summary of the reaction catalyzed by CotB2, showing the first steps in which GGPP is converted to the C1, C15, and C8 carbocations (A, B, and C), followed by many steps leading to the final carbocation D and then to the product cyclooctat-9-en-7-ol.
Figure 8.

Pertinent portion of the X-ray structure of the enzyme CotB2 with the unreactive substrate GGSPP bound in the active site proximate to W186. The distance measurement shown is in Å units.
As Tomita et al.,23 as well as Major and co-workers,28 have emphasized, the elaborate folding of GGPP in the active site of CotB2 serves to facilitate all of the many steps that involve carbocations in the reaction sequence from GGPP to product. This precise folding is observed23 in the X-ray structure of the active site containing unreactive surrogate substrate GGSPP, which differs from GGPP only by replacement of O by S as the atom connecting GG to P, relatively distant from C15. This X-ray structure shows C14 only 3.17 Å from C10,23 the atom to which C14 bonds to form the C15 carbocation (A to B, Figure 9). It has not been previously noted that this same folding of GGSPP also places C15 only 3.93 Å from C8, the atom from which a hydride transfer to C15 converts B to allylic carbocation C. Using PyMOL,50 we added hydrogen atoms (colored magenta in Figure 9) to C8 to provide an estimate of 2.96 Å for the distance between C15 and the hydrogen atom to be transferred from C8.51 Wu and co-workers,24 on the basis of QM/MM calculations, report a C15–H–C8 distance of 2.57 Å. These C15–H distances are obviously approximate, but they do provide additional evidence that the folding of GGSPP can facilitate the hydride transfer that effects the conversion of carbocation B to allylic carbocation C (Figure 9). The stereochemistry we show of the C8 hydrogen that is transferred to C15 is the same as that indicated for this reaction by Raz et al.28 The intricate substrate folding that places C8, as well as C10, close to C15 means that negligible conformational change is required for the conversion of B to C, permitting this reaction to occur essentially immediately after B is formed, with a calculated energy barrier of only 6.4 kcal/mol.28 Based on this precise geometric organization of GGSPP in the X-ray of the active site CotB2, it is reasonable to conclude that the reaction of the natural substrate GGPP in the same active site takes place in the same manner. This active site geometry also furnishes hydrophobic protection of the intermediate carbocations from unwanted nucleophilic quenching, as discussed further below.
Figure 9.

Carbocation intermediates A, B, and C in the CotB2-catalyzed reaction are shown with an emphasis on the folding of GGSPP in the active site that facilitates the formation and subsequent reaction of carbocation B, with measurements of the distances between the atoms involved in these two reactions shown in Å units. The hydrogens added to C8 of GGSP are shown in magenta.
Returning to the effort to evaluate tryptophan stabilization energy in a carbocation-π interaction, we first calculated the energies of optimized complexes at distances between C15 and C4 ranging in 0.2 Å increments from 2.0 to 7.0 Å. To conform to measurements made on the X-ray structure23 (Figure 8), the equilibrium π4 complex 8 was first modified by changing the angle ∠C7–C4–C1552 from 91.3 to 97.5° and the dihedral angle ∠C2–C3–C8–C9 from −96.0 to −80.2°. As mentioned earlier, the angle ∠C7–C4–C15 of 97.5° clearly shows that carbocation-π interaction is preferred over the periphery of the ring rather than over some ring centroid, a preference which we postulated and for which we provided supporting evidence.29 With these modifications held constant, the binding energies of optimized complexes at each distance were determined, analogously to the study reported previously31,32 for complexes of ethylbenzene with the t-butyl cation, to afford the results displayed in graphic form in Figure 10.
Figure 10.

Distance dependence of the M06/cc-pVTZ-optimized binding energy for the t-butyl cation–3-ethylindole complex based on the geometry of the π4 complex 8, slightly modified to resemble the X-ray structure shown in Figure 8.
An additional complex at a binding distance of 4.14 Å (12) was of particular interest, of course, because that is the distance from C4 of W186 to C15 of GGSPP in the X-ray structure (Figure 8). In the calculation of the binding energy of this 4.14 Å complex, the energy of the 3-ethylindole component was optimized with the same constraints, angle ∠C7–C4–C15 at 97.5° and dihedral angle ∠C2–C3–C8–C9 at −80.2°, used to obtain the data in Figure 10. When this 4.14 Å structure was optimized, it was immediately apparent that there is a striking resemblance of this complex 12, shown in Figure 11, to the comparable portion of the X-ray structure (Figure 8). The calculated binding energy of complex 12 is −15.7 kcal/mol, providing the first estimate of the π-complexation stabilization energy that a tryptophan residue can provide to a biochemical carbocation.
Figure 11.

M06/cc-pVTZ-constrained optimized structures and binding energies (kcal/mol) for complexes of the t-butyl cation with 3-ethylindole. The numbers representing distance measurements are in Å units. The numbers in magenta indicate the numbering system for the carbon atoms of the t-butyl cation.
Complex 12 was then refined, while maintaining the previous angular constraints, by use of numerous additional measurements of distances, angles, and dihedral angles on the portion comprising C15 and W186 in the X-ray structure (Figure 8), in order to replicate as closely as possible the geometry in the active site. The resulting refined model 13, shown in Figure 11, confirms the visually evident geometric similarity between complex 12 and the X-ray structure.23 Complex 13 afforded a stabilization energy of −15.3 kcal/mol, very similar to the −15.7 kcal/mol binding energy for 12. Any attempt to explain this small 0.4 kcal/mol difference must be made with caution, and it is not obvious from an examination of structures 12 and 13 why the former is calculated to be more stable. One possible contributing factor is that the angle ∠C4–C15–C14 in model 13 is held at 158.3°, the value measured on the X-ray structure, whereas that angle is 147.8° in optimized structure 12. The larger angle in the active site structure in Figure 8 probably fosters the geometric proximity and alignment of C14 to C10 to facilitate their bond formation (Figure 9), as discussed earlier.
The calculated values of −15.7 and −15.3 kcal/mol for the stabilization energies of complexes 12 and 13 are significantly greater than the value of −10.7 kcal/mol calculated for the constrained optimized t-butyl cation–ethylbenzene complex (shown as 14 in Figure 12) at the same binding distance of 4.14 Å. An analysis40 of the occupancies of the valence π-type NAO’s39 shows a net π donation of 0.107 for complex 12 compared to a value of 0.024 for complex 14, suggesting that part of the binding energy difference results from the greater π-electron-donating ability of 3-ethylindole. A difference in contributions from C–H−π interactions is also likely to be important. Estimates of the C–H−π stabilization energies for models 12 and 14 were obtained by calculating the binding energy changes that result when the shortest C–H–Cring distances (2.45 and 2.48 Å in complex 12 and 2.71 and 2.86 Å in complex 14) were significantly increased to reduce the C–H−π interaction. This was achieved by rotating the relevant methyl groups around the C(Me)–C+ axis in a way that also avoids creating new, short C–H–Cring distances.53 The binding energy change thus calculated for complex 12 was 3.1 kcal/mol, whereas that for complex 14 was 1.6 kcal/mol. These values suggest that stabilization from C–H−π interactions not only contributes to binding in both complexes but also enhances the binding in complex 12 to a greater extent.
Figure 12.

Model 14. The M06/cc-pVTZ-constrained optimized structure and binding energy (kcal/mol) for the t-butyl cation–ethylbenzene π complex with the C+ -- C1 distance fixed at 4.14 Å. The numbers representing distance measurements are in Å units.
All the calculations described herein were done in the gas phase with a dielectric constant ε = 1, and the method of analysis used does not allow any estimate of the effect of the actual dielectric constant in the presumably rather hydrophobic active sites of the enzymes involved. For hydrophobic enzyme active sites of this type, values of ε in the range of 2–4 are considered appropriate.54 We have previously calculated the carbocation-π binding energy at different values of ε of the continuous medium for model structure 1,31 and analogous calculations for complex 12(55) indicate that the stabilization energy for complex 12 would be reduced from −15.7 kcal/mol to approximately −9 to −6 kcal/mol at values of ε = 2–4. However, the dielectric constant of the continuous medium does not describe the local environment of any individual molecule. Further analysis of the X-ray structure presented in Figure 8 shows that one side of the C15 carbocationic site is protected by the folding of the bound GGSPP. This places the hydrocarbon chain C14–C10 directly in line behind that C15 carbocation, facilitating formation of the bond between C14 and C10 (Figure 9) and providing a nonpolar hydrocarbon shield on that side of C15, as shown in Figure 13 (Figure 8 provides a different perspective of this geometry). On the other side of C15, where it is not already proximate to the hydrocarbon portion of W186, it is essentially covered by the hydrocarbon portions of two leucines (L216 and L281). These two residues, along with W186 on one face, and the hydrocarbon portion of GGSPP on the opposite face of the C15 carbocation, provide a protective hydrophobic shell for the C15 carbocation (Figure 13). The resulting local effective dielectric constant in which the carbocation intermediate is imbedded is thus likely to be at the low end of the 2–4 ε range. The results described herein confirm that the remarkably intricate folding of the substrate GGSPP in the active site of CotB2 furnishes a surrounding protective hydrophobic shell and an array of precisely placed residues that facilitate both the formation and further reaction of the C15 intermediate carbocation. They also afford an evaluation of the stabilization that this folding provides to that C15 carbocation through its proximity in the active site to W186, the first such estimate involving tryptophan as the π donor to a biochemical carbocation.
Figure 13.

Portion of the X-ray structure of the enzyme CotB2 showing the hydrophobic shell provided by L216, L281, and W186 and part of the hydrocarbon chain of GGSPP surrounding the putative carbocation at C15. The 70% transparent spheres represent the van der Waals volumes of the associated atoms.
Conclusions
Employing the same strategy used in previous efforts31,32 to evaluate the stabilization energy provided by a phenylalanine residue to a biochemical carbocation intermediate via carbocation-π complexation, we have now studied tryptophan as the π donor in such complexes. Initially, a general investigation was conducted on the complexation properties of indole and 3-ethylindole with the t-butyl cation in order to get useful background information concerning the properties of complexes involving these binding partners. As expected, they showed a more varied reactivity than did ethylbenzene in our earlier work, affording equilibrium σ complexes at all ring atoms and equilibrium π complexes at C4, C7, C3a, and C7a. The latter two complexes are of special interest because the only previous study of indole–t-butyl cation complexation reported only one equilibrium π complex in the C3a-C7a region.10 The structures of the C3a and C7a equilibrium π complexes involving indole show that geometries permitting good C–H−π interactions of both its pyrrole ring and its benzene ring with hydrogen atoms of two methyl groups of the t-butyl cation are important contributors to enhanced binding.
With this background information, we sought literature reports of X-ray structures with an unreactive surrogate ligand for the putative carbocation and a tryptophan residue in reasonable proximity to that putative carbocationic site. Among the available possibilities, one reported by Tomita et al.23 showed a particularly clear and promising relationship between W186 and C15 of GGSPP at a distance of 4.14 Å. This X-ray structure also provided measurements affording modest new insight into the mechanism at C15 during the CotB2-catalyzed reaction. To get a general idea of what to expect for π complex geometry as a function of binding distance, we evaluated the binding energy of optimized C4-π complexes of 3-ethylindole with the t-butyl cation at binding distances from 2.0 to 7.0 Å in 0.2 Å increments while enforcing certain angular relationships in the complexes. The binding energy at 4.14 Å, the distance measured on the X-ray structure between C4 of W186 and C15 of GGSPP, was of course of particular interest and was found to be −15.7 kcal/mol, providing the first estimate of the stabilization energy that can be conferred by tryptophan via carbocation-π complexation of a biochemical carbocation intermediate. The similarity in appearance of the pertinent portion of the X-ray structure to this −15.7 kcal/mol complex, constructed with minimal reference to that X-ray structure, is striking. A model was then created that conformed as closely as possible to measurements made on that active site X-ray structure. This model afforded a calculated stabilization energy of −15.3 kcal/mol, close to the value of −15.7 kcal/mol obtained from optimization of the less carefully constructed model. The stabilization energy of −15.3 kcal/mol thus calculated for carbocation-π interaction with a tryptophan is significantly greater than the value of −10.7 kcal/mol we estimated for phenylalanine acting as a π donor in a π complex with the same binding distance of 4.14 Å. An analysis suggests that the enhanced binding for tryptophan results from both the greater π-electron-donating ability of 3-ethylindole compared to that of ethylbenzene and stronger C–H−π interactions. The X-ray structure23 also provides evidence that the putative carbocation at C15 is surrounded by a very hydrophobic shell created on one side by adjacent amino acids L216, L281, and W186 and on the other side by the adjacent hydrocarbon portion of GGSPP, indicating that the dielectric constant in the region local to that carbocationic center has a low value. The active site of enzyme CotB2 thus serves to protect the intermediate C15 carbocation in a highly nonpolar environment; to provide a very favorable geometric arrangement of the neighboring amino acid residues that facilitates both formation and reaction of that carbocation; and to stabilize the transient positive charge at C15 via carbocation-π interaction with W186.
Computational Methods
Computations were performed using the Gaussian 16 Rev. C0156 and CFOUR v1.057 software packages. Most calculations employed density functional theory with the M06 functional36 and the cc-pVTZ basis set,37 and the ultrafine grid option was used together with the weighting scheme of Stratmann et al.58 For all unconstrained optimizations, stationary points were characterized using vibrational frequencies calculated within the harmonic approximation. For each transition state, an intrinsic reaction coordinate calculation59−63 was used to identify equilibrium structures lying on a continuous path with the transition state. The very tight option was selected for all the Gaussian 16 geometry optimizations. Because structures for some of the model complexes are not fully optimized, vibrational frequency calculations were not performed on these systems, and thus, all reported energies do not include zero-point vibrational corrections.
We have validated31 the capability of the M06 functional for providing reliable structures and accurate binding energies for carbocation-π interactions by repeating an extensive set of computations at the CCSD(T)/cc-pVTZ level.37,42 Atomic charges and orbital occupancies were calculated using the natural bond orbital analysis developed by Weinhold and co-workers.39,64 The PyMOL Molecular Graphics System, Version 2.4.0 Schrödinger, LLC.50 was used extensively for depicting X-ray structures and for making measurements of distances and angles in portions of these structures. Tabulations of many of the measurements made on model complexes constructed to replicate the portion of their active sites comprising putative carbocation-π interactions are provided in the Supporting Information.
Acknowledgments
The authors thank a referee for insightful comments on the original manuscript. In addition, Dartmouth College is thanked for financial support.
Data Availability Statement
The data underlying this study are available in the published article and its Supporting Information.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c03259.
The authors declare no competing financial interest.
Supplementary Material
References
- a Christianson D. W. Structural and Chemical Biology of Terpenoid Cyclases. Chem. Rev. 2017, 117, 11570–11648. 10.1021/acs.chemrev.7b00287. [DOI] [PMC free article] [PubMed] [Google Scholar]; b Chem. Rev. 2018, 118, 11795, 10.1021/acs.chemrev.8b00682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dougherty D. A. Cation-π Interactions in Chemistry and Biology: A New View of Benzene, Phe, Tyr, and Trp. Science 1996, 271, 163–168. 10.1126/science.271.5246.163. [DOI] [PubMed] [Google Scholar]
- Ma J. C.; Dougherty D. A. The Cation−π Interaction. Chem. Rev. 1997, 97, 1303–1324. 10.1021/cr9603744. [DOI] [PubMed] [Google Scholar]
- Dougherty D. A. The Cation−π Interaction. Acc. Chem. Res. 2013, 46, 885–893. 10.1021/ar300265y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahadevi A. S.; Sastry G. N. Cation−π Interaction: Its Role and Relevance in Chemistry, Biology, and Material Science. Chem. Rev. 2013, 113, 2100–2138. 10.1021/cr300222d. [DOI] [PubMed] [Google Scholar]
- Davis M. R.; Dougherty D. A. Cation−π interactions: computational analyses of the aromatic box motif and the fluorination strategy for experimental evaluation. Phys. Chem. Chem. Phys. 2015, 17, 29262–29270. 10.1039/C5CP04668H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito R.; Hashimoto I.; Masukawa Y.; Hoshino T. Effect of Cation−π Interactions and Steric Bulk on the Catalytic Action of Oxidosqualene Cyclase: A Case Study of Phe728 of β-Amyrin Synthase from Euphorbia tirucalli L. Chem. – Eur. J. 2013, 19, 17150–17158. and references therein 10.1002/chem.201301917. [DOI] [PubMed] [Google Scholar]
- Faraldos J. A.; Antonczak A. K.; González V.; Fullerton R.; Tippman E. M.; Allemann R. K. Probing Eudesmane Cation−π Interactions in Catalysis by Aristolochene Synthase with Non-canonical Amino Acids. J. Am. Chem. Soc. 2011, 133, 13906–13909. and references therein 10.1021/ja205927u. [DOI] [PubMed] [Google Scholar]
- Chang C.-H.; Wen H.-Y.; Shie W.-S.; Lu C.-T.; Li M.-E.; Liu Y.-T.; Li W.-H.; Wu T.-K. Protein engineering of oxidosqualene-lanosterol cyclase into triterpene monocyclase. Org. Biomol. Chem. 2013, 11, 4214–4219. 10.1039/c3ob40493e. [DOI] [PubMed] [Google Scholar]
- Jenson C.; Jorgensen W. L. Computational Investigations of Carbenium Ion Reactions Relevant to Sterol Biosynthesis. J. Am. Chem. Soc. 1997, 119, 10846–10854. 10.1021/ja9714245. [DOI] [Google Scholar]
- Hess B. A. Jr. Concomitant C-Ring Expansion and D-Ring Formation in Lanosterol Biosynthesis from Squalene without Violation of Markovnikov’s Rule. J. Am. Chem. Soc. 2002, 124, 10286–10287. 10.1021/ja026850r. [DOI] [PubMed] [Google Scholar]
- Hess B. A. Jr.; Smentek L. The Concerted Nature of the Cyclization of Squalene Oxide to the Protosterol Cation. Angew. Chem., Int. Ed. 2013, 52, 11029–11033. 10.1002/anie.201302886. [DOI] [PubMed] [Google Scholar]
- Chen N.; Wang S.; Smentek L.; Hess B. A. Jr.; Wu R. Biosynthetic Mechanism of Lanosterol: Cyclization. Angew. Chem., Int. Ed. 2015, 54, 8693–8696. 10.1002/anie.201501986. [DOI] [PubMed] [Google Scholar]
- Hess B. A. Jr. Computational studies on the cyclization of squalene to the steroids and hopenes. Org. Biomol. Chem. 2017, 15, 2133–2145. 10.1039/C7OB00222J. [DOI] [PubMed] [Google Scholar]
- Hong Y. J.; Tantillo D. J. C–H···π interactions as modulators of carbocation structure – implications for terpene biosynthesis. Chem. Sci. 2013, 4, 2512–2518. 10.1039/c3sc50571e. [DOI] [Google Scholar]
- Hong Y. J.; Tantillo D. J. Tension between Internal and External Modes of Stabilization in Carbocations Relevant to Terpene Biosynthesis: Modulating Minima Depth via C–H···π Interactions. Org. Lett. 2015, 17, 5388–5391. 10.1021/acs.orglett.5b02740. [DOI] [PubMed] [Google Scholar]
- Hong Y. J.; Tantillo D. J. The energetic viability of an unexpected skeletal rearrangement in cyclooctatin biosynthesis. Org. Biomol. Chem. 2015, 13, 10273–10278. 10.1039/C5OB01785H. [DOI] [PubMed] [Google Scholar]
- Hare S. R.; Pemberton R. P.; Tantillo D. J. Navigating Past a Fork in the Road: Carbocation−π Interactions Can Manipulate Dynamic Behavior of Reactions Facing Post-Transition-State Bifurcations. J. Am. Chem. Soc. 2017, 139, 7485–7493. 10.1021/jacs.7b01042. [DOI] [PubMed] [Google Scholar]
- Tantillo D.J.Comprehensive Natural Products III (3rd Edition), 2020, 644–653.
- Zev S.; Gupta P. K.; Pahima E.; Major D. T. A Benchmark Study of Quantum Mechanics and Quantum Mechanics-Molecular Mechanics Methods for Carbocation Chemistry. J. Chem. Theory Comput. 2022, 18, 167–178. 10.1021/acs.jctc.1c00746. [DOI] [PubMed] [Google Scholar]
- Sato H.; Teramoto K.; Masumoto Y.; Tezuka N.; Sakai K.; Ueda S.; Totsuka Y.; Shinada T.; Nishiyama M.; Wang C.; Kuzuyama T.; Uchiyama M. “Cation-Stitching Cascade”: exquisite control of terpene cyclization in cyclooctatin biosynthesis. Sci. Rep. 2016, 5, 18471–18476. 10.1038/srep18471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato H.; Narita K.; Minami A.; Yamazaki M.; Wang C.; Suemune H.; Nagano S.; Tomita T.; Oikawa H.; Uchiyama M. Theoretical Study of Sesterfisherol Biosynthesis: Computational Prediction of Key Amino Acid Residue in Terpene Synthase. Sci. Rep. 2018, 8, 2473–2481. 10.1038/s41598-018-20916-x. [DOI] [PMC free article] [PubMed] [Google Scholar]; Sato et al. used Tantillo’s computational approach to investigate the effect that C–H --π interaction between a carbocation intermediate and phenylalanine F191 of sesterfisherol synthase may have on the preferred ring cyclization pathway in the biosynthesis of sesterfisherol
- Tomita T.; Kim S.-Y.; Teramoto K.; Meguro A.; Ozaki T.; Yoshida A.; Motoyoshi Y.; Mori N.; Ishigami K.; Watanabe H.; Nishiyama M.; Kuzuyama T. Structural Insights into the CotB2-Catalyzed Cyclization of Geranylgeranyl Diphosphate to the Diterpene Cyclooctat-9-en-7-ol. ACS Chem. Biol. 2017, 12, 1621–1628. 10.1021/acschembio.7b00154. [DOI] [PubMed] [Google Scholar]; The X-ray structure of GGSPP in the active site of CotB2 has PDB code 5GUE
- Tang X.; Zhang F.; Zeng T.; Li W.; Yin S.; Wu R. Enzymatic Plasticity Inspired by the Diterpene Cyclase CotB2. ACS Chem. Biol. 2020, 15, 2820–2832. 10.1021/acschembio.0c00645. [DOI] [PubMed] [Google Scholar]
- Driller R.; Janke S.; Fuchs M.; Warner E.; Mhashal A. R.; Major D. T.; Christmann M.; Brück T.; Loll B. Towards a comprehensive understanding of the structural dynamics of a bacterial diterpene synthase during catalysis. Nat. Commun. 2018, 9, 1–8. 10.1038/s41467-018-06325-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Driller R.; Garbe D.; Mehlmer N.; Fuchs M.; Raz K.; Major D. T.; Brück T.; Loll B. Current understanding and biotechnological application of the bacterial diterpene synthase CotB2. Beilstein J. Org. Chem. 2019, 15, 2355–2368. 10.3762/bjoc.15.228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raz K.; Driller R.; Brück T.; Loll B.; Major D. T. Understanding the role of active site residues in CotB2 catalysis using a cluster model. Beilstein J. Org. Chem. 2020, 16, 50–59. 10.3762/bjoc.16.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raz K.; Driller R.; Dimos N.; Ringel M.; Brück T.; Loll B.; Major D. T. The Impression of a Nonexisting Catalytic Effect: The Role of CotB2 in Guiding the Complex Biosynthesis of Cyclooctat-9-en-7-ol. J. Am. Chem. Soc. 2020, 142, 21562–21574. 10.1021/jacs.0c11348. [DOI] [PubMed] [Google Scholar]; Raz et al. have calculated detailed free energy profiles of all steps involving carbocation intermediates in the CotB2-catalyzed reaction the gas phase, in chloroform solution, and bound to CotB2
- Miklis P. C.; Ditchfield R.; Spencer T. A. Carbocation−π Interaction: Computational Study of Complexation of Methyl Cation with Benzene and Comparisons with Related Systems. J. Am. Chem. Soc. 1998, 120, 10482–10489. 10.1021/ja980505d. [DOI] [Google Scholar]
- Ditchfield R.; Spencer T. A. Carbocation-π interaction: the 1,1-dimethylallyl cation and benzene. Tetrahedron Lett. 2011, 52, 3674–3677. 10.1016/j.tetlet.2011.05.036. [DOI] [Google Scholar]
- Ditchfield R.; Spencer T. A. Carbocation−π interaction: evaluation of the stabilization by phenylalanine of a biochemical carbocation intermediate. Org. Biomol. Chem. 2016, 14, 9543–9548. 10.1039/C6OB01761D. [DOI] [PubMed] [Google Scholar]; Figure 2 of this reference documents the validity of the M06/cc-pVTZ method for studying the distance dependence of carbocation - π binding between the t-butyl cation and an aromatic system
- Spencer T. A.; Ditchfield R. A simpler method affords evaluation of π stabilization by phenylalanine of several biochemical carbocations. Org. Biomol. Chem. 2020, 18, 7597–7607. 10.1039/D0OB01565B. [DOI] [PubMed] [Google Scholar]
- Köksal M.; Chou W. K. W.; Cane D. E.; Christianson D. W. Structure of Geranyl Diphosphate C-Methyltransferase from Streptomyces coelicolor and Implications for the Mechanism of Isoprenoid Modification. Biochemistry 2012, 51, 3003–3010. 10.1021/bi300109c. [DOI] [PMC free article] [PubMed] [Google Scholar]; This X-ray structure has PDB Code 3VC1
- Chen M.; Al-lami N.; Janvier M.; D’Antonio E. L.; Faraldos J. A.; Cane D. E.; Allemann R. K.; Christianson D. W. Mechanistic Insights from the Binding of Substrate and Carbocation Intermediate Analogues to Aristolochene Synthase. Biochemistry 2013, 52, 5441–5453. 10.1021/bi400691v. [DOI] [PMC free article] [PubMed] [Google Scholar]; This X-ray structure has PDB Code 4KUX
- Thoma R.; Schulz-Gasch T.; D’Arcy B.; Benz J.; Aebl J.; Dehmlow H.; Hennig M.; Stihle M.; Ruf A. Insight into steroid scaffold formation from the structure of human oxidosqualene cyclase. Nature 2004, 432, 118–122. 10.1038/nature02993. [DOI] [PubMed] [Google Scholar]; This X-ray structure has PDB Code 1WGK
- Zhao Y.; Truhlar D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
- Dunning T. H. Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
- Ditchfield R.; Spencer T. A. (Unpublished results).
- Reed A. E.; Curtiss L. A.; Weinhold F. Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 1988, 88, 899–926. 10.1021/cr00088a005. [DOI] [Google Scholar]
- Details of this type of analysis are given in the Supporting Information.
- These values are calculated from the data reported in Tables 1 and S1 (given in the Supporting Information). Introduction of the 3-ethyl group produces similar, small enhancements in the binding for π-complex 4 (0.7 kcal/mol) and π-complex 7 (1.2 kcal/mol). As described in the Supporting Information, effects on the σ-complex binding energies are more varied.
- Bartlett R. J.; Musiał M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291–352. and references therein 10.1103/RevModPhys.79.291. [DOI] [Google Scholar]
- M06/cc-pVTZ calculated values for binding energies including zero-point vibrational energy corrections, binding enthalpies, and binding Gibbs free energies are included in the Supporting Information.
- For each π complex, calculations were performed to establish variation of the binding energy for small changes in the t-butyl cation – 3-ethylindole equilibrium separation. Typically, a change of ±0.2Å in the equilibrium C+–Cring distance produced a corresponding change of ≤0.5 kcal/mol in the energy of the complex. This energy variation is of similar magnitude to the stabilization associated with C–H -- π interactions in these π complexes.
- For the M06 and CCSD(T) π complex structure in ref (31)., root-mean-square differences (RMSD’s) for bond lengths, valence angles and dihedral angles are 0.008Å, 0.9 and 1.5°, respectively. Corresponding RMSD’s for the M06 and CCSD(T) ipso-σ complex structure are 0.007Å, 0.3 and 0.9°.
- Underestimation of binding in the carbocation σ complexes considered in this work is also found when the M06 functional is replaced by other, frequently used hybrid-functionals (Ditchfield, R.; Spencer, T. A. unpublished results).
- a Caruthers J. M.; Kang I.; Rynkiewicz M. J.; Cane D. E.; Christianson D. W. Crystal Structure Determination of Aristolochene Synthase from the Blue Cheese Mold Penicillium roqueforti. J. Biol. Chem. 2000, 275, 25533–25539. 10.1074/jbc.M000433200. [DOI] [PubMed] [Google Scholar]; b Whittington D. A.; Wise M. L.; Urbansky M.; Coates R. M.; Croteau R. B.; Christianson D. W. Bornyl diphosphate synthase: Structure and strategy for carbocation manipulation by a terpenoid cyclase. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 15375–15380. 10.1073/pnas.232591099. [DOI] [PMC free article] [PubMed] [Google Scholar]; c Hofmann E.; Zerbe P.; Schaller F. The Crystal Structure of Arabidopsis thaliana Allene Oxide Cyclase: Insights into the Oxylipin Cyclization Reaction. Plant Cell 2006, 18, 3201–3217. 10.1105/tpc.106.043984. [DOI] [PMC free article] [PubMed] [Google Scholar]; d Aaron J. A.; Lin X.; Cane D. E.; Christianson D. W. Structure of Epi-Isozizaene Synthase from Streptomyces coelicolor A3(2), a Platform for New Terpenoid Cyclization Templates. Biochemistry 2010, 49, 1787–1797. 10.1021/bi902088z. [DOI] [PMC free article] [PubMed] [Google Scholar]; e Ronnebaum T. A.; Gardner S. M.; Christianson D. W. An Aromatic Cluster in the Active Site of epi-Isozizaene Synthase Is an Electrostatic Toggle for Divergent Terpene Cyclization Pathways. Biochemistry 2020, 59, 4744–4754. 10.1021/acs.biochem.0c00876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blank P. N.; Pemberton T. A.; Chow J.-Y.; Poulter C. D.; Christianson D. W. Crystal Structure of Cucumene Synthase, a Terpenoid Cyclase That Generates a Linear Triquinane Sesquiterpene. Biochemistry 2018, 57, 6326–6335. 10.1021/acs.biochem.8b00899. [DOI] [PMC free article] [PubMed] [Google Scholar]; describe the X-ray crystal structure of cucumene synthase which shows four residues, F58, Y77, F78 and W310, in the active site surrounding the computationally introduced product cucumene in positions favourable for carbocation-π interactions with putative carbocation intermediates. A very similar arrangement (F57, F77, F78 and W308) appears in the X-ray structure of pentalenene synthase (Lesburg, C. A.; Zhai, G.; Cane, D. E.; Christianson, D. W. Crystal Structure of Pentalenene Synthase: Mechanistic Insights on Terpenoid Cyclization Reactions in Biology. Science1997, 277 (5333), 1820–1824)
- a Starks C. M.; Back K.; Chappell J.; Noel J. P. Structural Basis for Cyclic Terpene Biosynthesis by Tobacco 5-Epi-Aristolochene Synthase. Science 1997, 277, 1815–1820. 10.1126/science.277.5333.1815. [DOI] [PubMed] [Google Scholar]; b Wendt K. U.; Lenhart A.; Schulz G. E. The structure of the membrane protein squalene-hopene cyclase at 2.0 Å resolution. J. Mol. Biol. 1999, 286, 175–187. 10.1006/jmbi.1998.2470. [DOI] [PubMed] [Google Scholar]; c Paschall C. M.; Hasserodt J.; Jones T.; Lerner R. A.; Janda K. D.; Christianson D. W. Convergence of Catalytic Antibody and Terpene Cyclase Mechanisms: Polyene Cyclization Directed by Carbocation−π Interactions. Angew. Chem., Int. Ed. 1999, 38, 1743–1747. . [DOI] [PubMed] [Google Scholar]; d Rynkiewicz M. J.; Cane D. E.; Christianson D. W. Structure of trichodiene synthase from Fusarium sporotrichioides provides mechanistic inferences on the terpene cyclization cascade. Proc. Natl. Acad. Sci. U. S. A. 2001, 98, 13543–13548. 10.1073/pnas.231313098. [DOI] [PMC free article] [PubMed] [Google Scholar]; e Thoma et al. state in ref. 35 that W387 and W581 are also positioned for carbocation-π interaction at C6 and C10, and that H232 is also positioned for carbocation-π interaction at C14 and C20 of lanosterol.; f Kersten R. D.; Diedrich J. K.; Yates J. R. III; Noel J. P. Mechanism-Based Post-Translational Modification and Inactivation in Terpene Synthases. ACS Chem. Biol. 2015, 10, 2501–2511. 10.1021/acschembio.5b00539. [DOI] [PMC free article] [PubMed] [Google Scholar]; g Zhang F.; Chen N.; Wu R. Molecular Dynamics Simulations Elucidate Conformational Dynamics Responsible for the Cyclization Reaction in TEAS. J. Chem. Inf. Model. 2016, 56, 877–885. 10.1021/acs.jcim.6b00091. [DOI] [PubMed] [Google Scholar]
- The PyMOL Molecular Graphics System, Version 2.4.0; Schrödinger, LLC. [Google Scholar]
- The added C8–H bonds have the reasonable length of 1.09Å and the angle ∠H–C8–H is 114.9°.
- The designation C15 is used to indicate the C+ of the t-butyl cation in all the model structures representing complexes of W186 with GGSPP.
- Details of the approach employed are provided in the Supporting Information.
- Li L.; Li C.; Zhang Z.; Alexov E. On the Dielectric “Constant” of Proteins: Smooth Dielectric Function for Macromolecular Modeling and Its Implementation in DelPhi. J. Chem. Theory Comput. 2013, 9, 2126–2136. and references therein 10.1021/ct400065j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Details of the variation of the binding energy of complex 12 with dielectric constant ε are given in the Supporting Information.
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M. J.; Heyd J. J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Keith T. A.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford CT, 2016. [Google Scholar]
- CFOUR, a quantum chemical program package written by Stanton J. F.; Gauss J.; Harding M. E.; Szalay P. G. with contributions from Auer A. A.; Bartlett R. J.; Benedikt U.; Berger C.; Bernholdt D. E.; Bomble Y. J.; Cheng L.; Christiansen O.; Heckert M.; Heun O.; Huber C.; Jagau T.-C.; Jonsson D.; Jusélius J.; Klein K.; Lauderdale W. J.; Lipparini F.; Matthews D. A.; Metzroth T.; Mück L. A.; O’Neill D. P.; Price D. R.; Prochnow E.; Puzzarini C.; Ruud K.; Schiffmann F.; Schwalbach W.; Simmons C.; Stopkowicz S.; Tajti A.; Vázquez J.; Wang F.; Watts F.; and the integral packages MOLECULE (Almlöf J.; Taylor P. R.), PROPS (Taylor P. R.), ABACUS (Helgaker T.; Aa Jensen H. J.; Jørgensen P.; Olsen J.), and ECP routines by Mitin A. V.; van Wüllen C.. For the current version, see http://www.cfour.de.
- Stratmann R. E.; Scuseria G. E.; Frisch M. J. Achieving linear scaling in exchange-correlation density functional quadratures. Chem. Phys. Lett. 1996, 257, 213–223. 10.1016/0009-2614(96)00600-8. [DOI] [Google Scholar]
- Fukui K. The path of chemical reactions – the IRC approach. Acc. Chem. Res. 1981, 14, 363–368. 10.1021/ar00072a001. [DOI] [Google Scholar]
- Schlegel H. B. Optimization of equilibrium geometries and transition structures. J. Comput. Chem. 1982, 3, 214–218. 10.1002/jcc.540030212. [DOI] [Google Scholar]
- Page M.; McIver J. W. Jr. On evaluating the reaction path Hamiltonian. J. Chem. Phys. 1988, 88, 922–935. 10.1063/1.454172. [DOI] [Google Scholar]
- Page M.; Doubleday C. Jr.; McIver J. W. Jr. Following steepest descent reaction paths. The use of higher energy derivatives with ab initio electronic structure methods. J. Chem. Phys. 1990, 93, 5634–5642. 10.1063/1.459634. [DOI] [Google Scholar]
- Hratchian H. P.; Schlegel H. B. Using Hessian Updating To Increase the Efficiency of a Hessian Based Predictor-Corrector Reaction Path Following Method. J. Chem. Theory Comput. 2005, 1, 61–69. 10.1021/ct0499783. [DOI] [PubMed] [Google Scholar]
- Glendening E. D.; Reed A. E.; Carpenter J. E.; Weinhold F.. NBO Version 3.1.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data underlying this study are available in the published article and its Supporting Information.



