Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Jul 11;17(14):13554–13562. doi: 10.1021/acsnano.3c02107

Pure Graphene Acts as an “Entropic Surfactant” at the Octanol–Water Interface

Alireza Soleimani †,§, Herre Jelger Risselada †,‡,§,*
PMCID: PMC10373651  PMID: 37432037

Abstract

graphic file with name nn3c02107_0004.jpg

Graphene oxide (GO) has proved itself as a nanomaterial capable of acting as a surfactant by lowering the interfacial tension of the oil–water interface due to its polar oxygen groups. However, the surfactant behavior of the pure graphene sheet—since prevention of edge oxidation in experimental setups is nontrivial—is still an unresolved issue in graphene research despite significant progress in the field in recent years. Here, we conduct both atomistic and coarse-grained simulations to demonstrate that—surprisingly—even pristine graphene, which only consists of hydrophobic carbon atoms, is attracted to the octanol–water interface and consequently reduces its surface tension by 2.3 kBT/nm2 or about 10 mN/m. Interestingly, the location of the free energy minimum is not precisely at the oil–water interface itself but is rather buried about two octanol layers into the octanol phase, being about 0.9 nm from the water phase. We demonstrate that the observed surfactant behavior is purely entropically driven and can be attributed to the unfavorable lipid-like structuring of octanol molecules at the free octanol–water interface. In essence, graphene enhances the inherent lipid-like behavior of octanol at the water interface rather than directly acting as a surfactant. Importantly, graphene does not display surfactant-like behavior in corresponding Martini coarse-grained simulations of the octanol–water system since the free liquid–liquid interface loses essential structure at the lower coarse-grained resolution. However, a similar surfactant behavior is recovered in coarse-grained simulations of longer alcohols such as dodecan-1-ol and hexadecan-1-ol. The observed discrepancies at different model resolutions enable us to construct a comprehensive model of the surfactant behavior of graphene at the octanol–water interface. The here-gained insights may facilitate the broader utilization of graphene in numerous domains of nanotechnology. Furthermore, since a drug’s octanol–water partition coefficient is a crucial physicochemical parameter in rational drug discovery, we also believe that the universality of the here-illustrated entropic surfactant behavior of planar molecules deserves special attention in the drug design and development field.

Keywords: entropic surfactant, pristine graphene, interfacial tension, structure formation, directed self-assembly

Graphene, one of the most important nanomaterials, is a single-atom-thick planar sheet of sp2 bonded carbon atoms arranged in a hexagonal lattice. Graphene has been spotlighted as a shining star in the world of material science due to its exceptional physical and chemical properties, such as incredibly high tensile strength, excellent thermal conductivity, and tunable band gap.1−3 Nevertheless, despite boundless amounts of activity in graphene research, there are still unresolved issues about graphene’s other exhilarating properties, such as wetting transparency that enables the transmission of the substrate contact angle to the liquid on top of graphene. In this regard, Rafiee et al. demonstrated that a graphene monolayer is fully wetting transparent to surfaces such as silicon, copper, and gold, but wetting transparency breaks down on the glass surface, where the short-range chemical forces have a significant impact on the water contact angle.4 On the other hand, based on a combination of contact angle measurements and molecular dynamics simulations, Shih et al. demonstrated that the wetting transparency breaks down substantially on both superhydrophobic and superhydrophilic substrates, which classifies graphene as a material exhibiting partial wetting transparency.5 An interesting and closely related question in graphene literature is graphene’s ability to reduce the interfacial tension of liquid–liquid interfaces effectively,6−8 in other words, the surfactant nature of graphene. Thus, far, almost all studies have been centralized around graphene oxide or its derivatives, mainly because dispersing and individualizing pure graphene in solvents, melts, and matrices have been challenging and often impossible.9,10 In this context, Cote et al. demonstrated the amphiphilic nature of graphene oxide with an edge-to-center distribution of hydrophilic and hydrophobic domains. As a result, graphene oxide could adhere to the interface and function as a surfactant by lowering interfacial energy.11 However, one crucial question is still to be answered: whether or not the earlier mentioned surfactant behavior of graphene oxide is an intrinsic property of graphene or has emerged only due to the presence of hydrophilic oxygen groups such as hydroxyl, epoxide, and carboxyl on the basal plane and free edges, manifesting the coverage of graphene between 25% and 75%.12 To this aim, we have conducted atomistic and coarse-grained molecular dynamics simulations to investigate this yet unanswered question by measuring the interfacial tension of the octanol–water interface in the presence of pristine graphene. We will demonstrate that—surprisingly— even pristine graphene, which only consists of hydrophobic carbon atoms, is a surfactant at the octanol–water interface. Interestingly, graphene’s preferential location is not precisely at the oil–water interface itself but is rather buried about two octanol layers into the octanol phase, being about 0.9 nm from the water phase. Comprehending the physics that underlies the observed surfactant behavior of graphene at fluid–fluid interfaces sheds light on directing the self-assembly of graphene-based superstructures, such as sandwiched graphene-membrane systems,13 with interesting potential applications for the engineering of in situ sensing technology. Moreover, our findings may explain why graphene flakes studied by confocal Raman spectroscopy feature less uniform strain distributions and more residual strain at the water–octanol interface than at the water–air interface.8 Hence, our simulations predict that octanol domains can favorably form in between the water phase and the graphene sheet thereby potentially causing “wrinkling” or corrugation of the hexagonal lattice and concomitant strain. These insights may therefore guide the development of fluid-based approached for the improved handling of graphene, i.e., the ability to process larger graphene flakes without breaking them. Finally, we also believe that this research can grab scientists’ attention in the drug design and development field. Knowledge of a drug’s octanol–water partition coefficient is a crucial physicochemical parameter in rational drug discovery since it can be employed to identify candidate drugs. Specifically, Lipinski’s rule of five prioritized compounds with a calculated logarithm of the octanol–water partition coefficient of less than five as orally active drug candidates.14

Results and Discussion

Atomistic Setup: Effect of Pure Graphene on the Octanol–Water Interfacial Tension

In order to investigate the surfactant behavior of a pristine graphene sheet, the interfacial tension of the octanol–water interface was calculated as a function of the distance between the interface and a periodic graphene sheet. It also is worth pointing out that utilizing a periodic graphene sheet more realistically represents the macroscopic length scale of a pristine graphene flake located at the water-octanol interface, as studied by recent experiments,8 and whose area is in the square millimeter range. Therefore, our initial simulation set up contains a periodic graphene sheet (∼16 nm2) located in the middle of the simulation box and parallel to the xy plane. Conveniently, such a periodicity enables a trivial and precisely defined reaction coordinate invariant of thermal fluctuations of the interface, i.e., the interfacial thickness is derived from the molecular volume of a fixed number of octanol molecules sandwiched in between the graphene–water layer. The potential of mean force (PMF) per unit area is then directly given by the average surface tension measured in simulation.15 Corresponding simulations of nonperiodic graphene flakes are presented within the SI. The initial simulation system is comprised of a phase separated periodic octanol–water system (Figure 1a). The thickness of the octanol slab is approximately 8, whereas the water slab is approximately 5 nm thick. The graphene sheet is initially located within the octanol phase on 2 nm distance from the water interface. To decrease the distance from the water interface, i.e., the reaction coordinate of interest, octanol molecules are gradually removed from the initially 2 nm thick octanol slab above the graphene sheet (Figure 1a), until the slab is depleted. The opposite 4 nm thick octanol slab—the thicker slab below the graphene sheet—remains undisturbed and thus serves as a model of the octanol bulk phase. Therefore, the only distinction between our 33 simulated systems is the difference in the number of octanol molecules that exist in the slab above the graphene sheet, which translates to the distance between the graphene sheet and the octanol–water interface. As a result, the interfacial tension can be obtained from the simulations as follows:

graphic file with name nn3c02107_m001.jpg 1

where Px and Py represent the tangential components of the pressure, Pz is the normal component of the pressure tensor, and Lz is the length of the simulation box along the z-direction. Factor 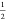Inline graphic accounts for the fact that there are two octanol–water interfaces in the simulation box, above and beneath the graphene sheet. The simulation results in Figure 1b indicate a decrease in surface tension when graphene approaches the octanol–water interface. The reported values are relative to the surface tension of the normal octanol–water interface. The surface tension reduction is maximal, −2.3 kBT/nm2, at 0.9 nm from the octanol–water interface. This implies that a graphene sheet or flake, if freely diffusing, most preferentially locates at this location, i.e., a free energy minimum. It is important to emphasize that this free energy reduction is relative to the free energy per area (surface tension) corresponding to the graphene sheet being located in the bulk octanol phase. Consequently, the measured reduction in surface tension can become larger than the reference surface tension of the octanol–water interface itself, being about 1.6 kBT/nm2 in the simulations. Furthermore, the existence of this free energy minimum along with a concomitant reduction in surface tension is also confirmed by our simulations of “free” nonperiodic graphene flakes (see Figure S4a). In addition, we also simulated the diffusion process of octanol molecules through a hole created in the center of a periodic graphene sheet, again demonstrating the existence of a free minimum (see Figure S2a). Given that 72 octanol molecules are still present within the slab, and given the total projected area of the interface, a surface tension reduction of 2.3 kBT/nm2 translates into a free energy per molecule of about 0.5 kBT. Such a small magnitude is consistent with the free energy per fluctuation mode (wavenumber) in thermally fluctuating systems. To dissect the energetic contributions that govern the observed surfactant behavior of graphene, the surface tension profile—the potential of mean force per unit area (PMF)—is decomposed into enthalpic and entropic components. The enthalpic contribution was determined from the average enthalpy of the simulation (Figure S1a). The enthalpy remained almost unchanged in the region between the bulk and the minimum surface tension, whereas the free energy decreased. This suggests that the decrease in free energy is solely due to an increase in entropy. Thus, the reduction in surface tension is an entropically driven process. Next, since it is difficult to envision how the “sandwiching” of octanol molecules at the liquid–liquid interface increases the translational entropy, we speculate that the entropic driving force likely stems from conformational and/or rotational entropy changes. First, the conformational entropy of the graphene sheet itself was calculated as a function of interface distance. Figure S1b demonstrates that there is only a slight increase in the entropy from 1204.7 (J/mol·K) to 1205.9 (J/mol·K) between the interface distances of 1.7 and 1.0 nm. Then the entropy experienced a rapid decrease to 1201.5 (J/mol·K) at an interface distance of 1.0 nm. This sharp reduction in the entropy indicates the presence of a well within the free energy potential, i.e., the region where the free energy potential displays its minimum, suppressing thermal height/bending fluctuations in the graphene sheet. Thus, the observed entropic driving force evidently stems from changes in the surrounding liquid(s). To this aim, we computed both conformational and rotational entropy of the octanol molecules as a function of distance by laterally dividing the system into 12 distinct octanol layers, each consisting of 26 molecules (see Figure 2c). To correct for the diffusive behavior of the octanol molecules in the course of the trajectory, a permutation reduction scheme is applied, which relabels the diffusing octanol molecules such that they effectively remain within the same slab/layer.16 Indeed, we observe that the presence of graphene (present at 6 nm) substantially increases both the conformational and rotational entropy of octanol at the liquid–liquid interface (present at 7 nm) with respect to the graphene-less liquid–liquid interface (present at 1 nm). In other words, the presence of graphene at the interface has improved both entropies significantly. Therefore, the system can reduce the total free energy by placing one side of the graphene sheet close to the otherwise more costly octanol–water interface. It is also worth pointing out that the average rotational entropy in the system was 40.0 (J/mol·K) per molecule, which is consistent with the values reported in the literature.17 Nevertheless, since the magnitude of the rotational entropy is about a factor 10 lower than the magnitude of the conformational entropy, it only accounts for a marginal fraction of the observed entropic driving force compared to changes in the conformational entropy.

Figure 1.

Figure 1

Open in a new tab

Simulation setup and reaction coordinate. (a) Snapshots of the atomistic simulation (side view) along the modeled reaction coordinate: We effectively model a scenario where graphene gradually approaches the octanol–water interface. Left and middle snapshots illustrate systems with an interface distance to the octanol–water of 0 and 1.7 nm, respectively, whereas the right snapshot represents the corresponding symmetric scenario, i.e., an interface distance of 4 nm. (b) Surface tension as a function of the distance from the octanol–water interface.

Figure 2.

Figure 2

Open in a new tab

Origin of the free energy minimum. (a) Simulation snapshot of the system with minimum surface tension. (b) Mass density profile in the system with minimum surface tension. The arrow illustrates a depletion in the local octanol density. (c) Conformational (blue) and rotational entropy (red) calculated for 12 distinct octanol layers. Graphene (yellow plate) substantially increases the entropy of the nearby octanol–water interface (z = 6 to 7 nm) with respect to the entropy of the distal free octanol–water interface (z = 0 to 1 nm). (d) The second order orientational parameter of octanol molecules related to the minimum surface tension structure. The error bars obtained via bootstrapping are in the same order of magnitude as the data points.

Furthermore, to gain more insights into the nature of the observed entropic attraction toward the liquid–liquid interface, the orientational order parameter was computed via the second-order Legendre Polynomial:18

graphic file with name nn3c02107_m003.jpg 2

where θz is defined as the angle between the normal direction of the graphene sheet and the vector formed by the oxygen atom within the polar head and the hydrophobic tail’s last carbon atom. According to the definition of the orientational order parameter, which can vary from −0.5 to 1, a zero value of Sz would correspond to a situation where there is no orientational order between the examined molecules, a value of 1 represents full order along the graphene sheet normal, and a value of −0.5 indicates the tendency of the octanol molecules to orient within a plane perpendicular to the director, with no preferred orientation within the plane. Figure 2d shows the orientation profile of octanol molecules in the configuration with the minimum interfacial tension as a function of z with a slab size of 0.2 nm. Notable, the horizontal axis (z) represents the “absolute” coordinate of the particles in the longitudinal dimension of the box rather than the relative distance to the octanol–water interface. Thus, the results demonstrate that the orientation is isotropic when the octanol molecules are in the bulk phase (2 nm < z < 4 nm). However, as the octanol molecules approach the graphene sheet (z = 5.5 nm) from both sides, the orientational order parameter is more likely to be close to −0.5. This undoubtedly indicates that the graphene sheet impose parallel ordering within the surrounding octanol molecules. It is worth noting that the orientational order parameter can not be measured at the two slabs nearest to the graphene sheet due to excluded volume-like behavior of the graphene in those regions. In addition, the strongest ordering of octanol molecules is observed at the liquid–liquid interface, demonstrating that molecules are instantly oriented as their polar hydroxyl group interacts with the water phase thereby resembling a liquid crystalline ordering analogous to the ordering of lipids in bilayer. This phenomenon is evidently associated with a high entropic cost which is likely due to the concomitant restriction of the area per molecule at the interface in order to reduce unfavorable hydrophobic exposure to the water phase. Therefore, the lipid-like ordering of octanol molecules at the octanol–water interface is most likely causal to the observed entropic attraction of graphene.

Coarse-Grained Setup: Universality of Surfactant Behavior

Since the current study aims to comprehensively assess the surfactant nature of a pure graphene sheet, in this final section, we employ coarse-grained simulations to explore the universality and independence on the model’s details of the observed surface tension minimum. Interestingly, the coarse-grained simulation results show that the surfactant behavior of graphene, observed in the atomistic simulations, does not appear using a two-site coarse-grained octanol model but is recovered using CG models of longer alcohols such as dodecan-1-ol (3-site model) and hexadecan-1-ol (4-site model). Furthermore, unlike atomistic simulations, where the actual reason for the existence of the minimum proved to be entropically dominated, the minimum in the CG simulations solely occurs due to enthalpic contributions. In fact, in both coarse-grained dodecan-1-ol and hexadecan-1-ol models, the enthalpy represents the free energy profile to a great extent (Figure 3a). In contrast, the enthalpy profile in the atomistic simulations differs from the free energy profile (Figure S1a). The absence of an entropic contribution in the coarse-grained dodecan-1-ol and hexadecan-1-ol models, is also indicated by the entropy–enthalpy decomposition obtained by taking the derivative of the PMF with respect to the temperature (Figure S5b). In correspondence to the atomistic simulations of octanol, the free energy minimum is located within the oil phase. The minimum position—with respect to the fluid–fluid interface—corresponds to 2.8 and 2.4 times the length scale of a dodecan-1-ol and hexadecan-1-ol molecule within the CG simulations, respectively (Figure 3c). As a matter of fact, this multiplication factor corresponds to the multiplication factor observed in the atomistic simulations of octanol, being about 2.0 times, after taking into account that the molecular length in the corresponding coarse-grained model of octanol is derived from the geometric center of the first four and last four carbon atoms within the atomistic model. Thus, all the different models yield a free energy minimum whose structure is of a consistent, similar nature. Furthermore, the observed factor of 2 up to 2.8 times the molecule length as well as visual inspection suggests that the alcohol chains are, in fact, structured in three different layers: a horizontal layer ordered by the graphene layer, a wiggling disordered layer at the bulk, and a perpendicular layer with respect to graphene at the interface (Figure 3b). Calculation of the order parameter shows that the 2-site CG model reacts to the presence of the water interface to a smaller extent compared to that of the 3-site and 4-site CG models. In contrast, the presence of a graphene layer similarly affects the order parameter in all the different CG models (Figure 3d). These observations necessitate the presence of solvent structure at the fluid–fluid interface for the free energy minimum to occur. This agrees with our hypothesis that structure formation at the oil–water interface but not the graphene layer is the primary driving force of surfactant behavior. Therefore, the minimum in the 2-site octanol model can not be observed since it lacks the earlier discussed structure formation. The appearance of structure formation at the fluid–fluid interface is also evident by a subtle depletion in local oil density close to the interface in the absence of graphene (see Figure 2b), and whose location well corresponds with the location of the free energy minimum. Therefore, if an alcohol molecule is long enough, it obtains lipid-like ordering at the liquid–liquid interface. Consequently, a depletion in oil density occurs at a distal location from the interface, which favors the presence of pristine graphene. A related but extreme manifestation of such a concept is the preference of graphene to locate in between the leaflets of lipid bilayers, i.e., graphene is effectively sandwiched by the two bilayer leaflets.13,19 In atomistic simulations, structure formation at the fluid–fluid interface is seemingly associated with an excess entropic cost, whereas it is associated with an enthalpic cost in CG simulations. This discrepancy can, however, be understood from the fact that the coarse-graining procedure, which reduces the number of degrees of freedom while matching the Gibbs free energy of the fine-grained system, must necessarily replace many of the entropic contributions in the fine-grained system with effective enthalpic ones. Accordingly, spontaneous processes in coarse-grained models typically tend to be enthalpically rather than entropically driven. Therefore, we emphasize that fluid–fluid interfaces provide a valuable tool for accessing potential limitations of coarse-grained models20−22 in modeling fluid interactions with graphene (this work) or graphene oxide (e.g., ref (23)).

Figure 3.

Figure 3

Open in a new tab

Coarse-grained simulations modeling a graphene sheet approaching the alcohol–water interface. (a) Surface tension (ST) and enthalpy (EN) as a function of the distance from the interface for various CG models. (b) Simulation snapshot of the coarse-grained system corresponding to the free energy minimum. The inset indicates the corresponding stacking of the three distinct layers observed in the simulations. (c) The total thickness of the stacked alcohol layers at the free energy minimum expressed in terms of molecular length (end-to-end distance). The point AA → CG is a reconstructed point to directly compare the end-to-end distance in the coarse-grained simulations with the atomistic simulation. (d) Second order orientational parameter of the various CG models. The two-site CG model (orange) shows a decreased ordering near the liquid–liquid interface (z = 9 and z = 17 nm) but not near graphene (z = 13.5 nm).

Finally, an interesting question is whether the surface-activity of pristine graphene also warrants caution when determining the octanol–water partitioning coefficient of potential drug candidates or toxins containing similar planar, rigid ring structures, such as common in steroid derivatives and alkaloids. Most of the commonly used experimental determination methods such as, for example, the shake-flask method24−26 are ineffective for the studying of surface-active compounds. Not only do surface-active molecules more favorably reside at the octanol–water interface than the individual bulk phases, they can also act as an emulsifier resulting in the presence of small, persistently stable octanol droplets within the water phase, and which actively entrap the surface-active compound under study. In essence, a 2D material such as graphene enhances the inherent lipid-like behavior of octanol at the water interface rather than acting as a direct surfactant. In fact, also small hydrophobic molecules such as hexane and benzene display a weak favorable partitioning at the octanol–water interface (Figure S11a), however, because of a smaller length-scale its free energy of absorption is so small that its residence time at the interface is still in the order of nanoseconds. Given that the hexagonal lattice site of graphene is 0.142 nm, and given a surface tension reduction of 2.3 kBT/nm2 (∼10 mN/m), a molecule would require 83 to 125 hexagons to obtain a free energy of absorption of 10 to 15 kBT, which are the typical values for common industrial surfactants.10 In this regard, we carried out a simulation where the graphene sheet was replaced with 90 individual benzene molecules (Figure S11c). Although the benzene molecules can be coined “surface active” based on their weak partitioning to the interface, they do not lower the surface tension with respect to the reference value of octanol–water systems, but in fact rather increase it by about +0.2 kBT/nm2 (<1 mN/m), quite in contrast to graphene flakes of varying sizes (Figure S4a). Benzene molecules do not show true surfactant behavior because of a significant simultaneous partitioning in bulk octanol thereby changing its actual bulk properties (Figure S11d). In other words, benzene molecules do not increase the so-called surface pressure Π, being defined as Π = σref – σ, with σ being the measured surface tension in the presence of the surfactant and σref the reference surface tension of the octanol–water interface, in contrast to larger graphene flakes (Figure S4a). Finally, it is important to note that the entropic cost of registration (translational entropy and mixing entropy) at the interface is much lower for rigid, planar nanomaterials than for flexible polymers. This is precisely why planar nanomaterials are more likely to magnify entropic surfactant effects. In conclusion, the here-discussed entropic surfactant effect is unlikely to significantly affect the measurement of octanol–water bulk partitioning coefficients for small molecules. However, our observations do raise the question whether bulk partitioning coefficients actually provide a solid model for biological lipid bilayers given the competitive ability of lipid-like ordered layers to entropically mediate partitioning.13,19

Conclusions

In this study, atomistic and coarse-grained molecular dynamics simulations were performed to investigate the surfactant nature of the pristine graphene sheet at the octanol–water interface. It is indicated that graphene sheet acts as a surfactant by reducing the interfacial tension of the octanol–water interface by 2.3 kBT/nm2 (∼10 mN/m) with respect to the graphene sheet being located within the octanol bulk phase. Such a surfactant behavior is not captured by a 2-site coarse-grained model of octanol but is recovered by 3- and 4-site models of larger alcohols such as dodecan-1-ol and hexadecan-1-ol. In all of these scenarios, the location of the free energy minimum is explained by the stacking of three molecular layers that are distinctly ordered with respect to graphene: A perpendicular layer, an isotropic layer, and a parallel layer. Our results indicate that structure formation, particularly at the fluid–fluid interface, which is not well captured by a 2-site coarse-grained model, plays a causal role in the observed surfactant behavior of graphene. We therefore postulate that 2D nanomaterials display surfactant behavior at the oil–water interface whenever the oil phase forms a sufficiently structured fluid–fluid interface. Finally, we believe that our research has shed light on an unexpected surfactant mechanism which is not based on a molecule’s amphiphilic nature but is rather based on a molecule’s ability to increase chain entropy at the oil–water interface.

Methods

Atomistic Simulations

A recently refined version of the L-OPLS force-field was employed to model octanol molecules, i.e., the original OPLS-AA force-field was used to model the hydroxyl headgroup of the octanols and the L-OPLS parameters were adopted to improve the interactions between the hydrocarbon tails.27 It is worth pointing out that the L-OPLS refinement circumvents the crystallization issue of the original OPLS-AA caused due to exaggerated attractive interactions between the alkane chains, achieved through the modification of several nonbonded parameters and dihedral angles.27 On the other hand, the TIP4P/EW,28 i.e., a reparameterized version of the standard TIP4P water model with Ewald techniques, was selected as the model of choice for water molecules, owing to its proven ability to provide dependable predictions for water structure and structural transition temperature.29 We emphasize that the here-chosen force-field combinations are mainly motivated by the accurate description of the octanol–water interface as well as their respective bulk phases. Accordingly, using the selected force-field combination, we conducted a 1 μs simulation and computed the interfacial tension of the octanol–water interface from the last 200 ns to be 1.64 ± 0.2 kBT/nm2 (6.74 ± 0.82 mN/m), which shows a very good agreement with the values reported in the literature either measured experimentally as 2.06 kBT/nm2 (8.47 mN/m)30 or calculated via MD simulations, i.e., 1.90 kBT/nm2 (7.81 mN/m).31 The carbon atoms belonging to periodic graphene sheet were considered uncharged Lennard–Jones spheres with a cross-section of σ = 0.34 nm, and a potential well depth of ϵ = 0.36 kJ/mol, corresponding to sp2 carbons in the AMBER96 force-field.32 In addition, C–C bond length of 1.42 Å, C–C–C bending angle of 120°, and C–C–C–C planar angles maintained by harmonic potentials with spring constants of 322.55 kcal/mol Å2, 53.35 kcal/mol rad2 and 3.15 kcal/mol, respectively. It is noteworthy that the force-field parameters of atomistic graphene utilized in this study have also been employed to model the behavior of graphene in other research studies, for example, in refs (33−35), where the mechanism of DNA adsorption on graphene and graphene oxide was studied.

The molecular dynamics package GROMACS was utilized to perform all simulations.36 Leap-frog algorithm was used to integrate Newton’s equations of motion with a time step of 1 fs. Conditionally convergent long-range electrostatic interactions were calculated by the smooth particle mesh Ewald method. The cutoff distance defining the real space was 1.2 nm, and the grid spacing for the reciprocal space was 0.12 nm with quadratic interpolation. Lennard–Jones interactions were evaluated by a single cutoff distance of 1.2 nm with long-range dispersion corrections for the energy and pressure. Periodic boundary conditions were employed in all three dimensions. The steepest descent algorithm was used to minimize energy, followed by a 200 ps molecular dynamics simulation in the canonical (NVT) ensemble to relax the initial structure. Subsequently, we regulated the system’s temperature at 298.15 K using the Nose-Hoover thermostat, and maintained a constant pressure of 1 bar using the Berendsen barostat, with a relaxation time of 1 ps for both temperature and pressure coupling. To measure the interfacial tension, we employed a semi-isotropic pressure coupling scheme, which fixed the xy plane with a compressibility of 0 while allowing the z dimension to vary and maintain a pressure with a compressibility of 1 × 10–5 1/bar. The center of mass translational velocity was removed at each step. Each simulation was equilibrated for 300 ns followed by 100 ns production runs. Finally, we note that the absolute value of the measured surface tension in the simulation is box area dependent because of the incompressible nature of graphene. In contrast, the change in surface tension (the relative surface tension) given a conserved box area is only due to graphene’s surfactant activity.

Coarse-Grained (CG) Simulations

In the coarse-grained simulations, water and octanol molecules were modeled using a MARTINI model such that, on average, four carbon atoms plus associated hydrogens are characterized by a single interaction site along with four actual water molecules mapped into one CG water bead.37 Therefore, three CG models were developed to represent octanol (C8H17OH), dodecan-1-ol (C12H25OH), and hexadecan-1-ol (C16H33OH). MARTINI octanol consists of two uncharged beads, one polar (P1 type), and one apolar (C1 type). Similarly, MARTINI dodecan-1-ol and hexadecan-1-ol are comprised of three and four uncharged beads, respectively, such that one bead (P1 type) represents the hydroxyl headgroup and the rest of the beads (C1 type) denote the hydrophobic tail groups. Since the graphene sheet is in a direct contact with alcohol molecules rather than water molecules, antifreeze particles were not used in the simulations. No abrupt changes or spikes observed in enthalpy (latent heat) were observed, and which are indicative of freezing events or phase transitions (see Figure S9). Graphene sheet was also modeled using coarse-grained MD simulation via a strain energy conservation approach. The Hamiltonian of the CG graphene consists of bonded and nonbonded interactions, as below:

graphic file with name nn3c02107_m004.jpg 3

where D0 = 196.38 kcal/mol and α = 1.55 Å–1 are the depth and a parameter associated with the width of the potential well of the bond, respectively. d0 = 2.8 Å—twice the atomic bond length—is the equilibrium distance of the bond, kθ = 409.40 kcal/mol is the spring constant of the angular bending potential, θ0 = 120° is the equilibrium angle, kϕ = 4.15 kcal/mol is the spring constant of the dihedral interaction, ϵ = 0.82 kcal/mol is the parameter representing the depth of the potential well, and σ = 3.46 Å—to ensure an interlayer equilibrium spacing of 3.35 Å—is the equilibrium distance between two nonbonded beads.22 It is worth noting that among 8 independent CG force-field parameters, d0, θ0, and σ are predetermined by CG mapping level since they are related to the geometrical characteristics of the model, whereas the other 5 parameters are calibrated to reproduce the mechanical properties of graphene. In order for the forces and their derivatives to be continuous at the cutoff radius, the nonbonded and electrostatic interactions are shifted to zero by the GROMACS shift function in the range 0.9–1.2 nm and 0.0–1.2 nm, respectively. Each CG simulation was run for 10 μs production run.

Entropy Calculations

Conformational Entropy

The conformational entropic contribution of the graphene sheet and octanol molecules was obtained from the formula for the entropy proposed by J. Schlitter,38 which is based on the approximation that each degree of freedom is represented by a quantum-mechanical harmonic oscillator. Hence, the frequency ω of each of the harmonic oscillators is specified by its classical variance ⟨x2⟩c via the equipartition theorem mω2⟨x2⟩c = kBT where m is the degree of freedom mass, kB is the Boltzmann’s constant, and T is the temperature. As a generalization of heuristic entropy for one degree of freedom, the following formula was then introduced by Schlitter for the calculation of entropy in many degrees of freedom:39

graphic file with name nn3c02107_m005.jpg 4

where e is the Euler’s number, ℏ is Planck’s constant divided by 2π, 1 is the unity matrix, M is the mass matrix, and σ represents the covariance matrix of atom-positional fluctuations, i.e., σij = ⟨(xi – ⟨xi⟩)(xj – ⟨xj⟩)⟩, in which x1, ..., x3N denote the Cartesian coordinates of the atoms.

Rotational Entropy

Estimation of rotational entropy is based on a truncated mutual information expansion and the K-nearest-neighbor algorithm on SO(3)n, which is applied to the permutationally reduced trajectories to calculate rotational entropy directly by sampling the configuration space probability density Q as S = −kB⟨logQ⟩.40 Accordingly, rotation of N octanol molecules can be described by the Hamiltonian, H({Li, ωi}) = τ({Li}) + V({ωi}), with angular momenta Li, orientations ωi ∈ SO(3), the kinetic energy τ, and the potential energy V described by a molecular force-field. Therefore, rotational entropy can be calculated according to the following relation:

graphic file with name nn3c02107_m006.jpg 5

where kB is the Boltzmann constant, h is the Planck’s constant, 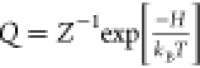Inline graphic is the normalized and dimensionless phase space density, and Z = ZτZV is the partition function.41

Acknowledgments

The authors would like to thank Liubov Belyaeva, Gregory Schneider, and Marcus Müller for fruitful discussions. The authors also thank Jeroen Methorst for sharing the Martini coarse-grained graphene generator script. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC 2033-390677874 – RESOLV. The authors additionally thank the NWO Vidi scheme project number 723.016.005 (The Netherlands), and the DFG grant number RI2791/2-1 (Germany) for funding.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.3c02107.

  • Enthalpy versus interface distance, conformational entropy of graphene and octanol molecules, diffusion process of octanol molecules through graphene hole, graphene–graphene van der Waals interaction, attraction of free flakes toward the interface, effect of nonperiodic free graphene flakes on the interfacial tension, surface tension as a function of temperature for a 3-site coarse-grained dodecan-1-ol model, noncovalent interactions between various components in the atomistic system as a function of the simulation time, density profile corresponding to the CG simulations, enthalpy without the presence of antifreeze particles, solely repulsive interactions graphene model, entropic surfactant effect for small hydrophobic molecules such as benzene and hexane with weak favorable partitioning at the octanol–water interface, and error propagation (PDF)

The authors declare no competing financial interest.

Supplementary Material

nn3c02107_si_001.pdf (3.7MB, pdf)

References

  1. Lee C.; Wei X.; Kysar J. W.; Hone J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. science 2008, 321, 385–388. 10.1126/science.1157996. [DOI] [PubMed] [Google Scholar]
  2. Balandin A. A. Thermal properties of graphene and nanostructured carbon materials. Nature materials 2011, 10, 569–581. 10.1038/nmat3064. [DOI] [PubMed] [Google Scholar]
  3. Castro Neto A. H.; Guinea F.; Peres N. M. R.; Novoselov K. S.; Geim A. K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. 10.1103/RevModPhys.81.109. [DOI] [Google Scholar]
  4. Rafiee J.; Mi X.; Gullapalli H.; Thomas A. V.; Yavari F.; Shi Y.; Ajayan P. M.; Koratkar N. A. Wetting transparency of graphene. Nature materials 2012, 11, 217–222. 10.1038/nmat3228. [DOI] [PubMed] [Google Scholar]
  5. Shih C.-J.; Wang Q. H.; Lin S.; Park K.-C.; Jin Z.; Strano M. S.; Blankschtein D. Breakdown in the wetting transparency of graphene. Physical review letters 2012, 109, 176101. 10.1103/PhysRevLett.109.176101. [DOI] [PubMed] [Google Scholar]
  6. Belyaeva L. A.; van Deursen P. M.; Barbetsea K. I.; Schneider G. F. Hydrophilicity of graphene in water through transparency to polar and dispersive interactions. Advanced materials 2018, 30, 1703274. 10.1002/adma.201703274. [DOI] [PubMed] [Google Scholar]
  7. Belyaeva L. A.; Schneider G. F. Wettability of graphene. Surf. Sci. Rep. 2020, 75, 100482. 10.1016/j.surfrep.2020.100482. [DOI] [Google Scholar]
  8. Belyaeva L. A.; Jiang L.; Soleimani A.; Methorst J.; Risselada H. J.; Schneider G. F. Liquids relax and unify strain in graphene. Nat. Commun. 2020, 11, 1–11. 10.1038/s41467-020-14637-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Kuziel A. W.; Milowska K. Z.; Chau P.-L.; Boncel S.; Koziol K. K.; Yahya N.; Payne M. C. The true amphipathic nature of graphene flakes: a versatile 2D stabilizer. Adv. Mater. 2020, 32, 2000608. 10.1002/adma.202000608. [DOI] [PubMed] [Google Scholar]
  10. McCoy T. M.; Turpin G.; Teo B. M.; Tabor R. F. Graphene oxide: a surfactant or particle?. Curr. Opin. Colloid Interface Sci. 2019, 39, 98–109. 10.1016/j.cocis.2019.01.010. [DOI] [Google Scholar]
  11. Cote L. J.; Kim J.; Tung V. C.; Luo J.; Kim F.; Huang J. Graphene oxide as surfactant sheets. Pure Appl. Chem. 2010, 83, 95–110. 10.1351/PAC-CON-10-10-25. [DOI] [Google Scholar]
  12. Boukhvalov D. W.; Katsnelson M. I. Modeling of graphite oxide. J. Am. Chem. Soc. 2008, 130, 10697–10701. 10.1021/ja8021686. [DOI] [PubMed] [Google Scholar]
  13. Titov A. V.; Král P.; Pearson R. Sandwiched graphene- membrane superstructures. ACS Nano 2010, 4, 229–234. 10.1021/nn9015778. [DOI] [PubMed] [Google Scholar]
  14. Mullard A. Re-assessing the rule of 5, two decades on. Nat. Rev. Drug Discov. 2018, 17, 777. 10.1038/nrd.2018.197. [DOI] [PubMed] [Google Scholar]
  15. Smirnova Y. G.; Aeffner S.; Risselada H. J.; Salditt T.; Marrink S.-J.; Müller M.; Knecht V. Interbilayer repulsion forces between tension-free lipid bilayers from simulation. Soft Matter 2013, 9, 10705–10718. 10.1039/c3sm51771c. [DOI] [Google Scholar]
  16. Reinhard F.; Lange O. F.; Hub J. S.; Haas J.; Grubmüller H. g_permute: Permutation-reduced phase space density compaction. Comput. Phys. Commun. 2009, 180, 455–458. 10.1016/j.cpc.2008.10.018. [DOI] [Google Scholar]
  17. Ali H. S.; Higham J.; Henchman R. H. Entropy of simulated liquids using multiscale cell correlation. Entropy 2019, 21, 750. 10.3390/e21080750. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Tan J. S.; Zhang L.; Lim F. C.; Cheong D. W. Interfacial properties and monolayer collapse of alkyl benzenesulfonate surfactant monolayers at the decane–water interface from molecular dynamics simulations. Langmuir 2017, 33, 4461–4476. 10.1021/acs.langmuir.7b00171. [DOI] [PubMed] [Google Scholar]
  19. Arjmandi-Tash H.; Lima L. M.; A. Belyaeva L.; Mukhina T.; Fragneto G.; Kros A.; Charitat T.; Schneider G. F. Encapsulation of graphene in the hydrophobic core of a lipid bilayer. Langmuir 2020, 36, 14478–14482. 10.1021/acs.langmuir.0c01691. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Williams C. D.; Lísal M. Coarse grained models of graphene and graphene oxide for use in aqueous solution. 2D Mater. 2020, 7, 025025. 10.1088/2053-1583/ab6f0c. [DOI] [Google Scholar]
  21. Monticelli L. On atomistic and coarse-grained models for C60 fullerene. J. Chem. Theory Comput. 2012, 8, 1370–1378. 10.1021/ct3000102. [DOI] [PubMed] [Google Scholar]
  22. Ruiz L.; Xia W.; Meng Z.; Keten S. A coarse-grained model for the mechanical behavior of multi-layer graphene. Carbon 2015, 82, 103–115. 10.1016/j.carbon.2014.10.040. [DOI] [Google Scholar]
  23. Lan T.; Zeng H.; Tang T. Molecular dynamics study on the mechanism of graphene oxide to destabilize oil/water emulsion. J. Phys. Chem. C 2019, 123, 22989–22999. 10.1021/acs.jpcc.9b05906. [DOI] [Google Scholar]
  24. De Bruijn J.; Busser F.; Seinen W.; Hermens J. Determination of octanol/water partition coefficients for hydrophobic organic chemicals with the “slow-stirring” method. Environmental Toxicology and Chemistry: An International Journal 1989, 8, 499–512. 10.1002/etc.5620080607. [DOI] [Google Scholar]
  25. Noble A. Partition coefficients (n-octanol—water) for pesticides. Journal of Chromatography A 1993, 642, 3–14. 10.1016/0021-9673(93)80072-G. [DOI] [Google Scholar]
  26. Andrés A.; Rosés M.; Ràfols C.; Bosch E.; Espinosa S.; Segarra V.; Huerta J. M. Setup and validation of shake-flask procedures for the determination of partition coefficients (log D) from low drug amounts. European Journal of Pharmaceutical Sciences 2015, 76, 181–191. 10.1016/j.ejps.2015.05.008. [DOI] [PubMed] [Google Scholar]
  27. Zangi R. Refinement of the OPLSAA force-field for liquid alcohols. ACS omega 2018, 3, 18089–18099. 10.1021/acsomega.8b03132. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Horn H. W.; Swope W. C.; Pitera J. W.; Madura J. D.; Dick T. J.; Hura G. L.; Head-Gordon T. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004, 120, 9665–9678. 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
  29. Jiao S.; Duan C.; Xu Z. Structures and thermodynamics of water encapsulated by graphene. Sci. Rep. 2017, 7, 1–9. 10.1038/s41598-017-02582-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Demond A. H.; Lindner A. S. Estimation of interfacial tension between organic liquids and water. Environ. Sci. Technol. 1993, 27, 2318–2331. 10.1021/es00048a004. [DOI] [Google Scholar]
  31. Liu Z.; Clark A. E. An octanol hinge opens the door to water transport. Chemical science 2021, 12, 2294–2303. 10.1039/D0SC04782A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Hummer G.; Rasaiah J. C.; Noworyta J. P. Water conduction through the hydrophobic channel of a carbon nanotube. nature 2001, 414, 188–190. 10.1038/35102535. [DOI] [PubMed] [Google Scholar]
  33. Zeng S.; Chen L.; Wang Y.; Chen J. Exploration on the mechanism of DNA adsorption on graphene and graphene oxide via molecular simulations. J. Phys. D: Appl. Phys. 2015, 48, 275402. 10.1088/0022-3727/48/27/275402. [DOI] [Google Scholar]
  34. Chen J.; Chen L.; Wang Y.; Chen S. Molecular dynamics simulations of the adsorption of DNA segments onto graphene oxide. J. Phys. D: Appl. Phys. 2014, 47, 505401. 10.1088/0022-3727/47/50/505401. [DOI] [Google Scholar]
  35. Muraru S.; Samoila C. G.; Slusanschi E. I.; Burns J. S.; Ionita M. Molecular dynamics simulations of DNA adsorption on graphene oxide and reduced graphene oxide-PEG-NH2 in the presence of Mg2. and Cl- ions. Coatings 2020, 10, 289. 10.3390/coatings10030289. [DOI] [Google Scholar]
  36. Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
  37. Marrink S. J.; Tieleman D. P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. 10.1039/c3cs60093a. [DOI] [PubMed] [Google Scholar]
  38. Schlitter J. Estimation of absolute and relative entropies of macromolecules using the covariance matrix. Chemical physics letters 1993, 215, 617–621. 10.1016/0009-2614(93)89366-P. [DOI] [Google Scholar]
  39. Schäfer H.; Daura X.; Mark A. E.; van Gunsteren W. F. Entropy calculations on a reversibly folding peptide: changes in solute free energy cannot explain folding behavior. Proteins: Struct., Funct., Bioinf. 2001, 43, 45–56. . [DOI] [PubMed] [Google Scholar]
  40. Heinz L. P.; Grubmuller H. Per— Mut: Spatially resolved hydration entropies from atomistic simulations. J. Chem. Theory Comput. 2021, 17, 2090–2098. 10.1021/acs.jctc.0c00961. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Heinz L. P.; Grubmuller H. Computing spatially resolved rotational hydration entropies from atomistic simulations. J. Chem. Theory Comput. 2020, 16, 108–118. 10.1021/acs.jctc.9b00926. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn3c02107_si_001.pdf (3.7MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES