Abstract

The interaction between nanoparticles includes several components; however, the most frequently used are electrostatic, caused by overlapping double electrical layers, and London–van der Waals interactions, caused by quantum and thermodynamic fluctuations of electromagnetic fields. Only these two kinds of interaction are considered below. The electrostatic interaction is calculated based on the linearized Poisson–Boltzmann equation for particles with constant electrical potential of the surfaces (constant ζ potentials). An exact solution of the problem is obtained for both identical particles and particles of different sizes. For the London–van der Waals interaction, the screening of static fluctuations and the retardation of electromagnetic fields for the dispersive part of the interaction are taken into account. The total interaction energy for two particles was calculated for a range of possible nanoparticle sizes from 1 to 103 nm and electrolyte concentration from 10–2 to 10–6 mol/L. The predominance of the London–van der Waals force over the shielded electrostatic repulsion force was found at high electrolyte concentrations in the range from 10–2 to 10–3 mol/L at large interparticle distances.
1. Introduction
Interaction forces between charged colloidal particles in aqueous electrolyte solutions play an important role in colloidal and interface science,1 biology, chemistry,2 etc. These forces determine the stability, dynamics, self-assembly, and many other properties of colloidal systems.3−5 In the case of sufficiently big colloidal particles (greater than 10–4 cm), these forces are well described by the classical theory referred to as6,7 Derjaguin–Landau–Verwey–Overbeck (DLVO) theory, which includes the forces of the electrical double-layer interaction with a characteristic region of action determined by the Debye length and the London–van der Waals interactions. At short distances, it is also necessary to take into account short-range forces associated with the molecular structure of the solvent, which are referred to as hydration/structural forces in the case of aqueous solutions.8−11
The interaction between nanoparticles includes the previously mentioned components, all of which have special features and are still under active investigation. The current state in this area is summarized by Kovalchuk et al.12 To describe the interaction of nanoparticles, approximations12 are used at the joint calculation of forces, both electrostatic and London–van der Waals interactions, which are based on the Deryaguin approximation.11 Recently, the electrostatic interaction was considered without the Deryaguin approximation based on the exact solution of the linearized Poisson–Boltzmann equation.13−22 New methods for the calculation of the strength of the London–van der Waals interaction were recently developed (see, for example, ref (23)). Below, an exact solution to the problem of the electrostatic interaction between nanoparticles based on the linearized Poisson–Boltzmann equation, which is supplemented by calculation of the London–van der Waals interaction force, is presented. Based on the developed method, the total interaction energy of nanoparticles was calculated for the range of ion concentrations in the electrolyte from 10 to 10–3 mM (1 mM = 10–3 mol/L) and nanoparticle sizes from 1 to 103 nm. Below, the interaction forces associated with the finite size of the electrolyte molecules are not taken into account, a modern description of which can be found in refs (8−10).
2. Shielded Electrostatic Interaction
The geometry of the problem of the electrostatic interaction between two nanoparticles in the electrolyte solution is presented in Figure 1. Earlier,15−18 the effect of the size of charged nanoparticles on their electrostatic interaction in an equilibrium plasma was studied in the framework of the linearized Poisson–Boltzmann model. Below, the problem is solved using another method of re-expansion of the products of the Macdonald function and Legendre polynomials, which are computationally simpler. Below, main attention is paid to the solution of the problem particle interaction of considerably different sizes, which causes certain numerical difficulties in describing the electrostatic interaction even in vacuum.24,25
Figure 1.
Geometry of the interaction of nanoparticles of different sizes in electrolyte solution: qi, ϕi0, ai, and εi are the charge, surface potential, radius, and dielectric permittivity of particles i = 1 and 2, respectively; ri is the radius vector of a point P, outside particles, taken from the center of the corresponding Oi; θi is the polar angle in a spherical coordinate system with the origin in the center of a corresponding particle, the axis directed to the center of the other particle; R is the distance between particle centers, ε is the dielectric permittivity of the medium between particles, and kD is the inverse Debye length of the electrolyte solution.
The linearized Poisson–Boltzmann equation for distribution of electric potential, ϕ(r, θ), around two nanoparticles in a binary electrolyte solution in a spherical coordinate system for axially symmetric charge distributions is
| 1 |
where kD is the inverse Debye length of the electrolyte solution
| 2 |
z1 and z2 are the charge numbers of ions, n10 and n20 are their bulk concentrations, e is the proton charge, ε is the dielectric permittivity of the electrolyte, and T is the temperature in energetic units.
The general solution of eq 1 for the electric potential of the system presented in Figure 1 associated with the kth particle (k = 1, 2) in a spherical coordinate system with a pole at the center of this particle is determined by the following expression
| 3 |
where Ak,n is the expansion coefficient and kn is the modified spherical Bessel function of the 3rd kind
| 4 |
where Kn+1/2 is the modified Bessel function of the 3rd kind.26 The detailed solution is presented in Appendix A.
In Figure 2a, distributions are shown for the reduced electrostatic potential
of two identical dielectric nanoparticles for the case of the constant surface potential with those in Figure 2b for the case of the constant surface free charge densities. These figures show that in the first case, the electric potential does not exceed the surface potential of the nanoparticles anywhere and remains constant inside the nanoparticles. In the second case (Figure 2b), near the nanoparticles, the electric potential exceeds the potential of the surface of solitary nanoparticles
| 5 |
and increases inside the nanoparticles when moving from the far edge to the edge closest to the other nanoparticle.
Figure 2.
Two-dimensional (2D) distributions of the reduced electrostatic potential, ψ = ϕ/ϕ10, of two identical dielectric nanoparticles for the case of the constant surface potentials (a) and the constant surface free charge densities (b) at n10 = n20 = 10–2 mM, a1 = a2 = 100 nm, L = 100 nm, ϕ10 = ϕ20 = 18 mV, nmax1 = nmax2 = 81 (a) and 80 (b), ε1 = ε2 = 2.557 (polystyrene), and ε = 80.1.
Using eqs 60 and 61 from Appendix A for the electrostatic force of interactions and neglecting terms, which include e–2kDR and higher order possible to conclude
| 6 |
where L̃ = kD(R – a1 – a2). After integration of the latter equation, it results in the well-known Derjaguin’s potential of electrostatic interaction27
| 7 |
The interaction potential in the case of the constant surface potentials was obtained by Reiner and Radke28
| 8 |
where S1 and S2 are nanoparticle surfaces. Integration of the latter expression results in
| 9 |
where q1,∞ and q2,∞ are the charges of the nanoparticles at R = ∞ [see eq 56]. Numerical calculations have shown that the potential of the electrostatic interaction determined using eq 9 and found by integrating the dependence of the interaction force on the interparticle distance differs no more than the accuracy of solving eq 43 by the LU-decomposition method.
For the electrostatic interaction in electrolyte solution between nanoparticles of different radii and different surface potentials,29 (see also ref (30) where the identical particles are considered), the following relation was deduced
 |
10 |
where Λ and Γ are as follows
In Figure 3, the dependencies are presented for the reduced force on the distance between the surfaces of particles with a radius of a1 = a2 = 100 nm for various electrolyte concentrations from 10 to 10–3 mM. It can be seen that with an increase in the concentration of ions and accordingly an increase in the screening constant, the interaction forces at small distances increase, and at large distances at L ≫ kD–1, they coincide with the DLVO dependence (eq 6).
Figure 3.
Dependence of the reduced force on the distance between the surfaces of nanoparticles with a radius of 100 nm at an electrolyte concentration of 10–3 (curve 1), 10–2 (2), 10–1 (3), 1 (4), and 10 mM (5). The solid curves are the results of the numerical calculation, and the dash-dotted curves are the differentiation of expression 10.
From Figure 3, one can conclude that the McCartney and Levine approximation according to eq 10 gives a reasonably good agreement with the exact solution at high electrolyte concentrations. As the electrolyte concentration decreases, the discrepancies increase.
Figure 4 shows that the approximation given by eq 10 works well only at high electrolyte concentrations (Figure 4b) and if nanoparticle radii do not differ too considerably. Considerably, discrepancies between our data and eq 10 are because the latter equation is applicable only if the applicability condition kDa1 > 5 is met.29 At electrolyte concentrations of 10–2 mM, the inverse Debye length kD = 10–2 nm–1. Therefore, the applicability condition is satisfied only for particles with a radius of 103 nm. Considerable discrepancies occur for nanoparticles with a size of 1 nm, since in this case, kDa1 = 10–2, which is much less than 5, and the applicability condition is violated.
Figure 4.
Dependence of the reduced force at an electrolyte concentration of 10–2 mM (a) and 10 mM (b) on the distance between the surfaces of nanoparticles with radii a1 = 100 nm and a2 = a1 (curves 1 and 5), a2 = 10 nm (2, 6), a2 = 1 nm (3, 7), and a2 = 1 μm (4, 8). The curves 1–4 are the results of the numerical calculation; the curves 5–8 are the differentiation of eq 10.
Figures 3 and 4a,b proves that with an increase in the concentration of the electrolyte, the force of the interaction approaches Deriaguin’s dependence eq 6 at smaller distances, while the particle size has little effect on these distances.
3. London–van der Waals Interaction
The electrostatic interaction, considered above, in the case of the same surface potentials of nanoparticles results in repulsion only. If it is the case, then, all nanosuspensions would be always stable and not coagulate. It is obviously not always the case, nanosuspensions are frequently unstable and coagulate. The latter means that there is one or even more than one attractive interaction/interactions. One of these attractive interactions is the London–van der Waals interaction, which was originally included into the so-called DLVO theory.11
The theory of the London–van der Waals interaction started from the previous work,31 where summation of the London pair interaction of all atoms of the system was undertaken. An expression was obtained for the particle interaction potential. Lifshitz32 developed a more precise theory of the interaction of two infinite flat dielectrics separated by vacuum. Dzyaloshinskii et al.33 developed a theory of interaction of two infinite flat dielectrics separated by a liquid. The general theory of the van der Waals interaction was later presented and reviewed (see, for example, refs (34−37)).
The London–van der Waals interaction energy is usually determined as23
| 11 |
where A0 is the zero-frequency energy contribution, A1 is the dispersion energy contribution to the Hamaker constant, fsc is the screening factor, FH is the Hamaker geometric factor, and Fg is the retarded geometric factor. The zero-frequency and dispersion contributions to the Hamaker constant are calculated according to23,38
| 12 |
| 13 |
where ℏ is the Planck constant, ε1(0) and ε2(0) are the static permittivities of medium 1 and 2, respectively, n01 and n02 are the refractive indices, ω1 and ω2 are the absorption frequencies, and the quantities nm, Δϵ0, X, and Y are defined by relations
| 14 |
 |
15 |
It supposed below that ω1 ≈ ωUV1 and ω2 ≈ ωUV2, where ωUV1 and ωUV2 are the boundaries of absorption zones in the ultraviolet region of the nanoparticle materials and the medium in which the nanoparticles are immersed, respectively. For water23 at 20 °C ε2(0) = 80.1, ωUV2 = 1.899 × 1016 s–1, n022 = 1.755, and λ0 = 99.26 nm. For polystyrene at 20 °C, ε1(0) = 2.557, εUV1 = 1.432 × 1016 s–1, and n01 = 2.447.
The screening factor in eq 11 is determined by the expression23
| 16 |
The Hamaker geometric factor in eq 11 is calculated from the expression31
| 17 |
where D1 and D2 are defined by
For the retarded geometric factor in eq 11, Vincent’s39 expressions are used
 |
18 |
 |
19 |
where as = 1.01, bs = 0.28π/λ0, aL = 2.45λ0/2π, bL = 2.04(λ0/2π)2, and Ls is the distance of a transition from the short-range expression 18 to the long-range expression 19
| 20 |
(a1, a2, and Ls in nm). In our calculations, Chen and Anandarajah’s40 retarded geometric factor was also used.
It was also proposed23 to calculate the London–van der Waals interaction energy as follows
| 21 |
with the retarded factor
| 22 |
where c is the velocity of light in vacuum. In ref (41) (see also refs (34) and (42)), an expression for the interaction energy was obtained without taking into account the retardation effects
| 23 |
where A131 is the Hamaker constant, which is taken as A131 = A0fsc + A1. The data necessary for the calculation of the Hamaker constants can be found in refs (43) and (44).
4. Results and Discussion
In Figure 6, curves 2–5 present the London–van der Waals force of interaction calculated using different approximations. This force at short distances becomes up to 4–5 orders of magnitude greater than the absolute value of the electrostatic repulsion force. At an electrolyte concentration of 10–2 mM at distances L ≈ 100 Å for nanoparticles of equal radii (Figure 5a, a1 = a2 = 100 nm) and at L ≈ 50 Å for nanoparticles of very different radii (Figure 5b, a1 = 1 nm, a2 = 100 nm), they become equal and then the electrostatic repulsion prevails. At a high electrolyte concentration of 10 mM (see Figure 6), the prevalence of electrostatic repulsion begins already at distances L ≈ 20 Å. For nanoparticles of the same radius, the London–van der Waals attraction begins to dominate again at distances L > 250 Å (see Figure 6a). For nanoparticles of very different radii, the London–van der Waals attraction dominates at distances L < 130 Å and L > 450 Å (see Figure 6b). This behavior is due to the fact that the dispersion part of the London–van der Waals interaction is not screened, and according to eq 19, at large distances, the interaction force becomes asymptotically as
| 24 |
However, at such distances the electrostatic repulsion is already close to the values given by the Deryaguin eq 6. Therefore, at large distances, the London–van der Waals attraction force decreases as R–8, and the strength of the electrostatic repulsion decreases exponentially. Therefore, at distances R < 1/kD, the rate of decrease of the first force with increasing R is noticeably higher than that of the second, and they eventually become equal. At distances R ≫ 1/kD, the London–van der Waals attraction again begins to dominate, as can be seen from Figure 6, but in Figure 5, due to the large shielding radius, this will happen outside the drawn region, where the forces already become negligible.
Figure 6.
Force dependencies similar to those shown in Figure 5 at a high electrolyte concentration of 10 mM for a1 = a2 = 100 nm (a) and a1 = 1 nm, a2 = 100 nm (b). Other notations are identical to those used in Figure 5.
Figure 5.
Dependencies of the electrostatic interaction (curve 1, the sign is reversed) and the London–van der Waals interaction on the smallest distance between the surfaces of polystyrene nanoparticles in the electrolyte at ϕ10 = ϕ20 = 18 mV, concentration of electrolyte n10 = n20 = 10–2 mM, a1 = a2 = 100 nm (a), and a1 = 1 nm, a2 = 100 nm (b). Curve 2 is calculated using the geometric factor from ref (40), 3—with the geometric factor (eqs 18 and 19),39 4—with free energy from expression 23 according to ref (41), and 5—with free energy from expression 21 according to ref (23).
Comparison of various methods for calculating the London–van der Waals attraction force, used in Figures 5 and 6, shows that
-
(1)
The geometric factors from refs (39) and (40) lead to practically identical results.
-
(2)
Taking into account the retardation phenomenon results in a noticeable decrease in the attraction force.
-
(3)
The scheme for calculating the interaction force proposed in ref (23) works quite well but somewhat overestimates the force, which is clearly seen from Figures 5a and 6a.
In ref (40), in contrast to ref (39) [see eqs 18 and 19], a single expression was proposed for calculating the geometric factor for all distances; therefore, the geometric factor from this work was used in calculations mentioned below. Note that expressions 18 and 19 results in a small jump in the interaction energy at the transition point from one approximation to the other, which is difficult to eliminate due to the dependence of the transition point on particle radii.
In Figure 7a,b, the interaction energy, U = UvdW + Usc,ϕ, is calculated based on eqs 9 and 11. In calculations, a geometrical factor is taken from ref (40); the electrostatic potential is calculated from eq 9. The insets in Figure 7 show the behavior of the interaction potential in the vicinity of the potential barrier between primary and secondary potential wells. The potential barrier and a secondary potential well (or its absence) are observed at different separations (different scales along the y-axis). According to the model used, the depth of the primary potential well is infinite, that is, coagulation in the primary potential well is always irreversible.
Figure 7.
Total interaction potential as a function of the shortest distance between the polystyrene nanoparticles at electrolyte concentrations of 10 (a) and 10–2 mM (b), ϕ10 = ϕ20 = 18 mV. Solid line: a1 = a2 = 100 nm; dash–dot line: a1 = 50 nm, a2 = 100 nm; dash–dot–dot line: a1 = 25 nm, a2 = 100 nm; and dashed line: a1 = 10 nm, a2 = 100 nm.
It is important to notice that according to Figures 7 and 8, in all cases considered, the potential barrier between the primary and secondary potential wells is relatively high and the height decreases with the electrolyte concentration (Figure 8) and strongly depends on the particle sizes (Figure 7a,b).
Figure 8.
Total interaction potential as a function of the shortest distance between the polystyrene nanoparticles at a1 = a2 = 100 nm, ϕ10 = ϕ20 = 18 mV, and different electrolyte concentrations: solid line: 1 mM, dashed line: 2 mM, dash–dot line: 5 mM, and dash–dot–dot line: 10 mM.
The 2nd insertion in Figure 7a shows a minimum at L ≈ 20 nm for all considered nanoparticle sizes. Consequently, at distances L > 20 nm between nanoparticles, an attractive force will act (see Figure 5), which can lead to effects such as the appearance of surface tension and the formation of weakly bound van der Waals complexes of nanoparticles. The depth of this well decreases as the electrolyte concentration decreases, and at n10 = n20 < 1 mM, it completely disappears. In this case, the interaction potential converges monotonically to the DLVO potential (eq 7). Consequently, only repulsion takes place between nanoparticles at large distances at low electrolyte concentrations.
At n10 = n20 = 10 mM, the Debye radius is 3.1 nm, so at distances where the potential well is observed in Figures 7 and 8, the potential energy ions are much less than the thermal energy, so the linearization of the Boltzmann distributions in the Poisson eq 1 is physically justified. Also, at L ≪ λ0 (for aqueous solutions λ0 ≈ 99.26 nm), the retardation effects are small and almost all used approximations at distances L ∼ 20 nm lead to the same values of the van der Waals force (see Figures 4 and 5). Therefore, we can conclude that the observed well in the total interaction potential at an electrolyte concentration of 1–10 mM has a physical meaning.
The dependencies of the total interaction potential of identical nanoparticles in a concentrated electrolyte at different values of their surface potential are presented in Figure 9. It can be seen that the surface potential has a noticeable effect on the behavior of the potential in the region of both extrema. With a decrease in the surface potential, the well depth increases, but the barrier height decreases, and at ϕ10 = ϕ20 < 6 mV, the extrema disappear altogether.
Figure 9.
Total interaction potential as a function of the shortest distance between the polystyrene nanoparticles at a1 = a2 = 100 nm, an electrolyte concentration of 10 mM, and different surface potentials: dash–dot line: ϕ10 = ϕ20 = 6 mV, dashed line: 8 mV, solid line: 9 mV, and dash–dot–dot line – 12 mV.
5. Conclusions
The interaction between nanoparticles including only two components, electrostatic repulsion and London–van der Waals attraction, was considered. Electrostatic repulsion is calculated based on the linearized Poisson–Boltzmann equation for particles with fixed electrical potential of the interfaces (constant ζ potentials). An exact solution for the problem is obtained for both identical particles and particles of different sizes. For the London–van der Waals attraction, the known models are used and compared. The total interaction energy for two particles was calculated for a range of possible nanoparticle sizes from 1 to 103 nm and electrolyte concentration from 10–3 to 10 mM. It is shown that for all nanoparticle sizes, the height of the potential barrier between primary and secondary minima is relatively high (order of 10kBT, kB is Boltzmann’s constant). The height decreases with the electrolyte concentration and strongly depends on the relation between nanoparticle sizes in the pair. At electrolyte concentrations from 1 to 10 mM, the formation of a potential well at distances of the order of L ≈ 200 Å was found. This shows that at distances L > 200 Å between nanoparticles, an attractive force acts due to the excess London–van der Waals attraction over the screened electrostatic repulsion; the latter can lead to the formation of weakly bound clusters of nanoparticles.
Acknowledgments
A.V.F. research was funded by the Russian Science Foundation (project No. 22-22-01000). V.S. research has received funding from the European Union’s Horizon 2020 research and an innovation programme under the Marie Skłodowska–Curie grant agreement No. 955612.
A. Detailed Solution for the Problem of the Screened Electrostatic Interaction
To find the coefficients Ak,n from the boundary conditions, we need to find the re-expansion coefficients of the potential of the ith particle, written in terms of Legendre polynomials with a pole at the center of this particle and in terms of Legendre polynomials with a pole at the center of the kth macroparticle, for which we use the addition formula13,34
| 25 |
where r̃i = kDri, r̃k = kDrk, R̃ = kDR, R is the distance between the centers of nanoparticles, and i = 1, 2, k = 3 – i, in(x) are the modified spherical Bessel functions of the 1st kind
| 26 |
In+1/2 is the modified Bessel functions of the first kind,26 and coefficients Lmn are determined by the following sum
| 27 |
| 28 |
Γ(x) is the γ function
| 29 |
In expression 25 and below, tilde-marked dimensionless values
reduced
to the Debye radius: x̃ = kDx. Note that 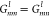 , and hence, Lnm = Lmn.
, and hence, Lnm = Lmn.
Coefficients 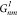 can be easily calculated using recurrent
relations
can be easily calculated using recurrent
relations
| 30 |
| 31 |
 |
32 |
In eq 31, values G(n+1)m0 are calculated initially for n = 0 for all m = n + 1, n + 2, ··· and after that for n = 1 for all m and so on.
Finally, for the potential of the ith nanoparticle, we obtain an expression in terms of Legendre polynomials with a pole at the center of the kth nanoparticle
| 33 |
where coefficients bnm are determined by the following expression
| 34 |
In refs (15−18), the coefficients bnm were determined as double sums of products of modified Bessel functions of 1st and 3rd kinds; however, expression 34 includes only one summation for calculation of Lmn. In spite of that, numerical calculations proved that coefficients bnm, calculated according to (eq 34) and according to equations presented in refs (15) and (16), coincide within the error limits of double-precision calculations on the computer.
A.1. Constant Free Charge Density of the Nanoparticles
In this case, the boundary conditions are as follows45,46
| 35 |
 |
36 |
where ϕI and ϕII are the electric potential inside of the 1st and 2nd nanoparticles, respectively, ε1 and ε2 are their dielectric permittivities, and σ1 and σ2 are their free surface charge densities.
The general solutions of the Laplace equations, taking into account the requirement that the potential inside nanoparticles should be finite, can be written as45,46
 |
37 |
where Cn and Dn are the expansion coefficients.
Using expressions 33 and 37, from the boundary conditions (expressions 35 and 36) for the expansion coefficients of ϕ1 and ϕ2, we obtain a system of equations (n = 0, 1, ···)
 |
38 |
where coefficients αn and βnm are determined by the following relations
 |
39 |
σk,n is the expansion coefficient of the surface charge density in terms of Legendre polynomials
It is taken into account here that we are considering a surface charge distribution that is axially symmetric with respect to the z-axis. In the case of a uniform distribution of free charge, only the term with n = 0 is non-zero
In a plasma or electrolyte, in many cases, the surface potential of macroparticles, ϕi,0, turns out to be constant and coinciding with the floating potential of the plasma (for more details, see ref (18); for the electrolyte concentrations and nanopartcile sizes considered, the case of constant surface potentials is implemented with a large margin). Therefore, in the present work, in which electrolytes with sufficiently high ion concentrations are studied, only this case will be considered.
A.2. Constant Potential of Nanoparticles
In the constant electric potential case, the system of equations for describing the expansion coefficients is greatly simplified. In this case, only one boundary condition is required for the continuity of the potential at the interface between dielectric media
| 40 |
From expressions 33 and 40, the following relation is derived (n = 0, 1, ···)
 |
41 |
From the second equation in (eq 41), A2,n can be found as
| 42 |
Substitution of the latter equation into the first eq 41 and after changing the order of summation, we get
| 43 |
Let us separately write down an equation for the case n = 0, taking into account that
 |
44 |
From eq 43, it can be concluded in the end
| 45 |
The system of eq 43 is solved by the method of LU-decomposition.47 Numbers of coefficients taken into account were nmax,1 for the smaller first nanoparticle and nmax,2 for the second nanoparticle. We can estimate coefficients A1,n and A2,n for n ≥ 1 from eq 41 as follows
| 46 |
Thus, in the calculation mentioned below, the required numbers, nmax,i, i = 1, 2, are defined from the following relation
| 47 |
with δ = 10–181. The upper boundary for numbers nmax,i was set to 1000, and the condition nmax,i ≥ 1 was fulfilled. The required numbers of expansion coefficients at different intersurface distances L are presented in Table 1 for the electrolyte concentration of 10–2 mM. With an increase in the electrolyte concentration, the number of required expansion terms increases slightly.
Table 1. Required Numbers nmax,i, i = 1, 2 for n10 = n20 = 10–2 mM, a2 = 100 nm, and δ= 10–181.
|
L = 0.1 nm |
L = 10 nm |
L = 103 nm |
||||
|---|---|---|---|---|---|---|
| a1 (nm) | nmax,1 | nmax,2 | nmax,1 | nmax,2 | nmax,1 | nmax,2 |
| 1 | 34 | 97 | 34 | 95 | 29 | 66 |
| 10 | 51 | 96 | 50 | 94 | 40 | 66 |
| 100 | 87 | 87 | 86 | 86 | 66 | 66 |
| 1000 | 161 | 68 | 161 | 68 | 135 | 62 |
The spherical modified Bessel functions at x = kDai, i = 1, 2 are calculated using the recurrent relations26
 |
48 |
First, the functions kn(x) are calculated for n = 1, 2, ···, nmax + 1 (nmax = 1000) starting from k0 and k1
 |
49 |
Then, using the continued fractions of Gauss48
| 50 |
| 51 |
the ratio in+1/in for n = nmax starting from k = 20 can be calculated. After that, the relation26 for cross-products
| 52 |
and the known values of kn(x) for n = nmax and nmax + 1 are used to calculate in(x) for n = nmax and nmax + 1. Ultimately, the functions in(x) are calculated for n = nmax – 1, ···, 1, 0 from the second recurrent relation 48. To check, the calculated data of the functions in for n = 0, 1 are compared with the obtained values from the well-known relations
 |
53 |
The spherical modified Bessel functions at x = kDR are calculated on basis of the first recurrent relation 48 for n = 0, 1, ···, nmax,2.
From boundary conditions for the continuity of the electric induction vector (eq 36), after simple transformations using relation 52, it is possible to deduce an expression for determination of the charges of the nanoparticles
| 54 |
If the distance between nanoparticles tends to be infinity, that is, R → ∞, the double electrical layers do not overlap and eq 41 reduces to
| 55 |
In this case from eq 54, the following well-known expressions for the relation of the charge of isolated nanoparticle with its surface potential
| 56 |
In the problem statement considered in this paper, only the z-component of the force is non-zero. To determine the force acting on the first particle, on the basis of the Maxwellian tension tensor, we find the expression (for more details, see refs (15) and (16))
| 57 |
where
 |
58 |
From eq 58 using eq 41, in the case of constant surface potentials of nanoparticles, it is possible to conclude
| 59 |
Finally, from eq 57, for the electrostatic interaction force, in the case of the constant surface potentials, the following expression is valid
| 60 |
At big separation, that is, at R → ∞, using solution (eq 55) and taking into account A1,1 from eq 57, it can be concluded that
 |
61 |
In refs (28) and (49), an expression was proposed for determining the density of surface forces associated with the osmotic pressure on the surface of nanoparticles, which in ref (50) was transformed into the usual Maxwellian tension tensor
| 62 |
For the problem considered here, the z-component of the Maxwellian tension tensor only is significant
Therefore, for the osmotic force, we get
 |
63 |
where Ψn is defined by eq 58. Equation 59 shows that in the case of constant surface potentials, this force vanishes. It should be noted that in the case of constant surface charge of nanoparticles, this force plays an important role, eliminating the inequality of the electrostatic forces acting on the first and second nanoparticles.15
The authors declare no competing financial interest.
References
- Israelachvili J. N.Intermolecular and Surface Forces, 3rd ed.; Elsevier: Amsterdam, 2011; pp 191–499. [Google Scholar]
- Honig B.; Nicholls A. Classical Electrostatics in Biology and Chemistry. Science 1995, 268, 1144–1149. 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- Manciu M.; Ruckenstein E. Role of the Hydration Force in the Stability of Colloids at High Ionic Strengths. Langmuir 2001, 17, 7061–7070. 10.1021/la010741t. [DOI] [Google Scholar]
- Wennerstrom H.; Vallina Estrada E.; Danielsson J.; Oliveberg M. Colloidal Stability of the Lliving Cell. Proc. Natl. Acad. Sci. U.S.A. 2020, 117, 10113–10121. 10.1073/pnas.1914599117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su S.; Siretanu I.; van den Ende D.; Mei B.; Mul G.; Mugele F. Facet-dependent Surface Charge and Hydration of Semiconducting Nanoparticles at Variable pH. Adv. Mater. 2021, 33, 2106229 10.1002/adma.202106229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Israelachvili J. N.Intermolecular and Surface Forces; Academic Press: Amsterdam, 2015. [Google Scholar]
- Liang Y.; Hilal N.; Langston P.; Starov V. Interaction Forces between Colloidal Particles in Liquid: Theory and Experiment. Adv. Colloid Interface Sci. 2007, 134-135, 151–166. 10.1016/j.cis.2007.04.003. [DOI] [PubMed] [Google Scholar]
- Kilpatrick J. I.; Loh S.-H.; Jarvis S. P. Directly Probing the Effects of Ions on Hydration Forces at Interfaces. J. Am. Chem. Soc. 2013, 135, 2628–2634. 10.1021/ja310255s. [DOI] [PubMed] [Google Scholar]
- Van Lin S. R.; Grotz K. K.; Siretanu I.; Schwierz N.; Mugele F. Ion-specific and pH-dependent Hydration of Mica-electrolyte Interfaces. Langmuir 2019, 35, 5737–5745. 10.1021/acs.langmuir.9b00520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klaassen A.; Liu F.; Mugele F.; Siretan I. Correlation between Electrostatic and Hydration Forces on Silica and Gibbsite Surfaces: An Atomic Force Microscopy Study. Langmuir 2022, 38, 914–926. 10.1021/acs.langmuir.1c02077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derjaguin B. V.; Churaev N. V.; Muller V. M.. Surface Forces; Consultants Bureau: New York, 1987. [Google Scholar]
- Kovalchuk N. M.; Johnson D.; Sobolev V.; Hilal N.; Starov V. Interaction between Nanoparticles in Nanosuspensions. Adv. Colloid Interface. Sci. 2019, 272, 102020 10.1016/j.cis.2019.102020. [DOI] [PubMed] [Google Scholar]
- Glendinning A. B.; Russel W. B. The Electrostatic Repulsion between Charged Spheres from Exact Solutions to the Linearized Poisson-Boltzmann Equation. J. Colloid Interface Sci. 1983, 93, 95–104. 10.1016/0021-9797(83)90388-0. [DOI] [Google Scholar]
- Carnie S. L.; Chan D. Y. C. Interaction Free Energy between Plates with Charge Regulation: a Linearized Model. J. Colloid Interface Sci. 1993, 161, 260–264. 10.1006/jcis.1993.1464. [DOI] [Google Scholar]
- Filippov A. V.; Derbenev I. N. Influence of the Size of Charged Spherical Macroparticles on Their Electrostatic Interaction in an Equilibrium Plasma. J. Exp. Theor. Phys. 2016, 150, 1262–1274. [Google Scholar]
- Derbenev I. N.; Filippov A. V.; Stace A. J.; Besley E. Electrostatic Interactions between Charged Dielectric Particles in an Electrolyte Solution. J. Chem. Phys. 2016, 145, 084103 10.1063/1.4961091. [DOI] [PubMed] [Google Scholar]
- Filippov A. V.; Derbenev I. N.; Pautov A. A.; Rodin M. M. Electrostatic Interaction of Macroparticles in Plasma in the Strong Shielding Regime. J. Exp. Theor. Phys. 2017, 125, 518–529. 10.1134/S1063776117080040. [DOI] [Google Scholar]
- Derbenev I. N.; Filippov A. V.; Stace A. J.; Besley E. Electrostatic Interactions between Charged Dielectric Particles in an Electrolyte Solution: Constant Potential Boundary Conditions. Soft Matter 2018, 14, 5480–5487. 10.1039/C8SM01068D. [DOI] [PubMed] [Google Scholar]
- Siryk S. V.; Bendandi A.; Diaspro A.; Rocchia W. Charged Dielectric Spheres Interacting in Electrolytic Solution: A Linearized Poisson-Boltzmann Equation Model. J. Chem. Phys. 2021, 155, 114114 10.1063/5.0056120. [DOI] [PubMed] [Google Scholar]
- Siryk S. V.; Rocchia W. Arbitrary-Shape Dielectric Particles Interacting in the Linearized Poisson-Boltzmann Framework: An Analytical Treatment. J. Phys. Chem. B 2022, 126, 10400 10.1021/acs.jpcb.2c05564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Y.-K. Electrostatics of Charged Dielectric Spheres with Application to Biological Systems. III. Rigorous Ionic Screening at the Debye-Hückel Level. Phys. Rev. E 2020, 102, 052404 10.1103/PhysRevE.102.052404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Obolensky O. I.; Doerr T. P.; Yu Y.-K. Rigorous Treatment of Pairwise and Many-body Electrostatic Interactions among Dielectric Spheres at the Debye-Hückel Level. Eur. Phys. J. E 2021, 44, 129 10.1140/epje/s10189-021-00131-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowen W. R.; Jenner F. The Calculation of Dispersion Forces for Engineering Applications. Adv. Colloid Interface Sci. 1995, 56, 201–243. 10.1016/0001-8686(94)00233-3. [DOI] [Google Scholar]
- Filippov A. V. Interaction between Two Charged Dielectric Balls with Strongly Different Radii. JETP Lett. 2022, 115, 174–180. 10.1134/S0021364022030067. [DOI] [Google Scholar]
- Filippov A. V. Electrostatic Interaction of a Charged Dielectric Sphere with a Flat Charged Interface between Homogeneous Dielectrics. J. Exp. Theor. Phys. 2022, 134, 590–599. 10.1134/S1063776122030141. [DOI] [Google Scholar]
- Watson G. N.A Treatise on the Theory of Bessel Functions; Cambridge University Press: London, 1922. [Google Scholar]
- Verwey E. J. W.; Overbeek J. T. G.. Theory of the Stability of Lyophobic Colloids; Elsevier: Amsterdam, 1948. [Google Scholar]
- Reiner E. S.; Radke C. J. Variational Approach to the Electrostatic Free Energy in Charged Colloidal Suspensions: General Theory for Open Systems. J. Chem. Soc., Faraday Trans. 1990, 86, 3901–3912. 10.1039/ft9908603901. [DOI] [Google Scholar]
- Bell G. M.; Levine S.; McCartney L. N. Approximate Methods of Determining the Double-layer Free Energy of Interaction between Two Charged Colloidal Spheres. J. Colloid. Interface Sci. 1970, 33, 335–359. 10.1016/0021-9797(70)90228-6. [DOI] [Google Scholar]
- McCartney L. N.; Levine S. An improvement on Derjaguinas Expression at Small Potentials for the Double Layer Interaction Energy of Two Spherical Colloidal Particles. J. Colloid Interface Sci. 1969, 30, 345–354. 10.1016/0021-9797(69)90401-9. [DOI] [Google Scholar]
- Hamaker H. C. The London-van der Waals Attraction between Spherical Particles. Physica 1937, 4, 1058–1072. 10.1016/S0031-8914(37)80203-7. [DOI] [Google Scholar]
- Lifshitz E. M. The Theory of Molecular Attractive Forces between Solids. Phys. JETP 1956, 2, 73–83. [Google Scholar]
- Dzyaloshinskii I. E.; Lifshitz E. M.; Pitaevskii L. P. Van Der Waals Forces in Liquid Films. J. Exp. Theor. Phys. 1960, 10, 161–170. [Google Scholar]
- Langbein D.Theory of Van der Waals Attraction, Springer Tracts in Modern Physics Hohler G., Ed.; Springer-Verlag: Berlin Heidelberg New York, 1974; Vol. 72. [Google Scholar]
- Derjaguin B. V.; Abrikosova I. I.; Lifshitz E. M. Molecular Attraction of Condensed Bodies. Phys.-Usp. 2015, 58, 906–924. 10.3367/UFNe.0185.201509i.0981. [DOI] [Google Scholar]
- Barash Y. S.; Ginzburg V. L. Some Problems in the Theory of Van der Waals Forces. Sov. Phys.-Usp. 1984, 27, 467–491. 10.1070/PU1984v027n07ABEH004025. [DOI] [Google Scholar]
- Churaev N. V. Surface Forces and Physicochemistry of Surface Phenomena. Russ. Chem. Rev. 2004, 73, 25–36. 10.1070/RC2004v073n01ABEH000867. [DOI] [Google Scholar]
- Horn R. G.; Israelachvili J. N. Direct Measurement of Structural Forces between Two Surfaces in a Nonpolar Liquid. J. Chem. Phys. 1981, 75, 1400–1411. 10.1063/1.442146. [DOI] [Google Scholar]
- Vincent B. The van der Waals Attraction between Colloid Particles Having Adsorbed Layers. II. Calculation of Interaction Curves. J. Colloid Interface Sci. 1973, 42, 270–285. 10.1016/0021-9797(73)90290-7. [DOI] [Google Scholar]
- Chen J.; Anandarajah A. Van der Waals Attraction between Spherical Particles. J. Colloid Interface Sci. 1996, 180, 519–523. 10.1006/jcis.1996.0332. [DOI] [Google Scholar]
- Mitchell D. J.; Ninham B. W. Van der Waals Forces between Two Spheres. J. Chem. Phys. 1972, 56, 1117–1126. 10.1063/1.1677331. [DOI] [Google Scholar]
- Langbein D. Non-retarded Dispersion Energy between Macroscopic Spheres. J. Phys. Chem. Solids 1971, 32, 1657–1667. 10.1016/S0022-3697(71)80059-8. [DOI] [Google Scholar]
- Bergström L. Hamaker Constants of Inorganic Materials. Adv. Colloid Interface Sci. 1997, 70, 125–169. 10.1016/S0001-8686(97)00003-1. [DOI] [Google Scholar]
- Parsegian V. A.; Weiss G. H. Spectroscopic Parameters for Computation of Van der Waals Forces. J. Colloid Interface Sci. 1981, 81, 285–289. 10.1016/0021-9797(81)90325-8. [DOI] [Google Scholar]
- Batygin V. V.; Toptygin I. N.. Problems in Electrodynamics, 2nd ed.; Academic Press: London, England, 1978. [Google Scholar]
- Smythe W. R.Static and Dynamic Electricity; Hemisphere Publications: New York Toronto London, 1950. [Google Scholar]
- Press W. H.; Vetterling W. T.; Teukolsky S. A.; Flannery B. P.. Numerical Recipes Example Book (FORTRAN); Cambridge University Press: Cambridge, 1992. [Google Scholar]
- Gautschi W.; Slavik J. On the Computation of Modified Bessel Function Ratios. Math. Comput. 1978, 32, 865–875. 10.1090/S0025-5718-1978-0470267-9. [DOI] [Google Scholar]
- Gilson M. K.; Davis M. E.; Luty B. A.; McCammon J. A. Computation of Electrostatic Forces on Solvated Molecules Using the Poisson-Boltzmann Equation. J. Phys. Chem. A 1993, 97, 3591–3600. 10.1021/j100116a025. [DOI] [PubMed] [Google Scholar]
- Lu B.; Cheng X.; Hou T.; McCammon J. A. Calculation of the Maxwell Stress Tensor and the Poisson-Boltzmann Force on a Solvated Molecular Surface Using Hypersingular Boundary Integrals. J. Chem. Phys. 2005, 123, 084904 10.1063/1.2008252. [DOI] [PubMed] [Google Scholar]











