Abstract
Myocarditis is cardiac damage caused by a viral infection. Its result often leads to a variety of arrhythmias. However, rapid and reliable identification of myocarditis has a great impact on early diagnosis, expedited treatment, and improved patient survival rates. Therefore, a novel strategy for the autonomous detection of myocarditis is suggested in this work. First, the improved quantum genetic algorithm (IQGA) is proposed to extract the optimal features of ECG beat and heart rate variability (HRV) from raw ECG signals. Second, the backpropagation neural network (BPNN) is optimized using the adaptive differential evolution (ADE) algorithm to classify various ECG signal types with high accuracy. This study examines analogies among five different ECG signal types: normal, abnormal, myocarditis, myocardial infarction (MI), and prior myocardial infarction (PMI). Additionally, the study uses binary and multiclass classification to group myocarditis with other cardiovascular disorders in order to assess how well the algorithm performs in categorization. The experimental results demonstrate that the combination of IQGA and ADE-BPNN can effectively increase the precision and accuracy of myocarditis autonomous diagnosis. In addition, HRV assesses the method’s robustness, and the classification tool can detect viruses in myocarditis patients one week before symptoms worsen. The model can be utilized in intensive care units or wearable monitoring devices and has strong performance in the detection of myocarditis.
Keywords: Electrocardiogram, Quantum genetic algorithm, Feature classification, Back propagation neural network, Myocarditis detection
Introduction
Research background
Myocarditis is a viral infection that mostly damages the myocardium, which can result in an irregular heartbeat [1]. For instance, patients with COVID-19 had nearly 18 times more risk of myocarditis when compared to individuals without COVID-19 [2]. Myocarditis typically strikes after middle age. The incidence rate often rises with age [3]. It can permanently harm the myocardium, especially in the elderly, and acute fulminant myocarditis may even be fatal. Its mortality rate is between 70 and 80 percent [4]. Myocarditis must be diagnosed quickly and accurately in order to prevent mortality. This is one of the most challenging diagnosis types in cardiology. Myocarditis can negatively affect the heart and cause abnormal ECG results [5]. Therefore, it is possible to diagnose myocarditis using real-time heart rate monitoring. Wearable technology can identify subtle changes in individual heartbeats [6] and assess the body’s immune system’s activity using heart rate variability indicators to determine whether a patient has myocarditis. Atrial fibrillation, ventricular arrhythmias (including ventricular tachycardia or ventricular fibrillation), and other arrhythmias are the most frequent ECG manifestations in patients with myocarditis [7]. ST-segment elevation [8], T-wave inversion [9], PR-interval prolongation [10], and other ECG abnormalities are among the ECG feature of myocarditis. Medical professionals can monitor myocarditis patients in real-time and determine which patients need intensive care by detecting myocarditis by ECG signals [5, 6].
Related research
Using artificial intelligence technology for ECG data analysis [11], such as machine learning (ML) [12] and deep learning (DL) [13] methods, they can accurately screen out diseases, and their accuracy is superior to other common screening methods. For the automatic detection of ECG signals, many deep learning theories have been introduced into the automatic diagnosis of cardiac arrhythmia in previous studies [14]. For example, empirical wavelet transform (EWT) [15–17], discrete wavelet transform (DWT) [18, 19], the adaptive threshold of a finite state machine [20], artificial neural network (ANN) [21], autoencoder (AE) [22], K-nearest neighbor (KNN) [23, 24, 35], support vector machine (SVM) [25, 26, 34, 35], convolutional neural network (CNN) [27, 28, 32, 37, 38, 41, 42], and multi-scale principal component analysis (MSPCA) [29, 30].
In recent years, people have studied the method of artificial intelligence to detect abnormalities of the heart and myocardial infarction by analyzing the ECG signal [31, 32]. Remya et al. [33] proposed ANN to classify the ECG of anterior wall myocardial infarction and inferior wall myocardial infarction by extracting features such as ST-segment potential shift, and their recognition rates were 93.61% and 86.15%, respectively. Sharma et al. [34] calculated the wavelet energy and covariance matrix at different scales through the wavelet transform of a multi-lead ECG as the diagnostic feature vector. Then, radial basis SVM and KNN algorithms were used to complete the classification of myocardial infarction in different parts, and their accuracy rates were about 96% and 99.58%, respectively. Sharma et al. [35] decomposed the ECG signal into different sub-bands by wavelet transform to extract features such as sample entropy, normalized sub-band, and logarithmic energy entropy. Then, the KNN algorithm and SVM were used to identify inferior wall myocardial infarction, and their identification rates were 98.69% and 98.84%, respectively. Hannun et al. [36] classified 12 heart rhythms using a deep neural network (DNN). In this algorithm, the average ROC (receiver operating characteristic) area for this approach is 0.97, and the average F1 score for DNN (0.837) was higher than that of cardiologists (0.780). Through the establishment of an 11-layer CNN, Acharya et al. [37] were able to detect single-lead myocardial infarction with an accuracy of 93.53%. In order to detect myocardial infarction by ECG detection, Lui et al. [38] employed CNN and recurrent neural networks, and the accuracy rate reached 92.4%. The signal was divided into each sub-band using a flexible analytical wavelet transform by Mohit et al. [39], who then computed the sample entropy as a feature. The classification accuracy is 99.31% when using a least-squares support vector machine (LS-SVM) to distinguish between myocardial infarction (MI) and non-MI. In order to achieve quick and precise intelligent identification of myocardial infarction, Han et al. [40] introduced a new multi-lead residual neural network (ML-ResNet) model that combines the ML-ResNet structure and the information recorded by the 12-lead ECG. This algorithm’s accuracy rate is 95.49%, and its F1 score in real-world use is 96.92%. A single-lead ECG-generative adversarial networks (SLC-GAN) approach for the automatic identification of myocardial infarction was put out by Li et al. [41]. Generative adversarial networks (GANs) and convolutional neural networks (CNNs) make up the model, which is a classifier.
Based on fivefold cross-validation, the MI classification accuracy of SLC-GAN reached 99.06%. Jahmunah et al. [32] proposed the DenseNet-CNN model to classify healthy subjects and 10 categories of myocardial infarction patients according to the location of myocardial involvement, which achieved high classification accuracy. Ko et al. [42] proposed an automatic detection model of Hypertrophic Cardiomyopathy (HCM), based on ECG signals using CNN. The model can automatically extract the deep features in the ECG signal and perform automatic detection of Background HCM, which has high diagnostic performance. Among the previous studies, there is no research on the application of deep learning to myocarditis disease detection. Therefore, we systematically reviewed the literature on cardiomyopathy-oriented disease diagnosis based on ECG signals. At the same time, DL has been successfully applied to the detection of heart-related images [43]. Using DL technology for classification modeling improves the performance of heart image classification methods. In addition, DL is also applied to the analysis and recognition of electroencephalogram (EEG) signals, for example, recurrent neural networks (RNN) [28], multi-scale principal component analysis (MSPCA) [16, 17, 28, 30], convolutional neural networks (CNN) [28, 44], and generative adversarial networks (GAN) [45].
Highlights
Due to the similarities in pattern between myocarditis and other cardiac-related illnesses, it might be challenging to distinguish between them during diagnostic tests [46, 47]. Myocarditis is identified by ECG signal analysis, and automatic diagnostic techniques are used to monitor ECG signals and render reliable judgments. This is due to the low cost of ECG signals in practical applications and the benefits of real-time monitoring of cardiac activity. An improved quantum genetic algorithm (IQGA) and an adaptive differential evolution-back propagation neural network (ADE-BPNN) are combined to create the myocarditis detection model proposed in this paper.
This model enhances the effectiveness of myocarditis feature extraction and the performance of classification accuracy to some amount, boosting the effect of myocarditis detection. The following is a summary of the contributions made by this work: (i) To extract the ECG characteristics of atrial fibrillation, ventricular fibrillation, and other arrhythmias, this research suggests an IQGA. An improved quantum revolving door genetic algorithm is proposed to address the limitations of the quantum genetic algorithm (QGA), which include poor local search capability and sluggish convergence speed. This algorithm improves accuracy and convergence speed by dynamically updating the rotation angle of the quantum revolving door. Additionally, the Hadamard gate is employed to execute chromosome update operations, achieve gene mutation effects, and realize QGA enhancement. (ii) This research suggests an ADE-BPNN to categorize the myocarditis-related aspects of the recovered ECG signal. The fundamental differential evolution algorithm is improved by adding an adaptive mutation operator to address the issue of sluggish convergence speed and easily slipping into the local minimum of BPNN. An ADE method is used to enhance the BPNN. The weight and threshold of the BPNN are optimized using the ADE algorithm, which addresses some of its drawbacks, including its sluggish convergence rate and its propensity to slip into the local extremum. iii) The suggested autonomous diagnosis model for myocarditis is capable of identifying minute variations in the patient’s heartbeat and determining whether the patient has concurrent myocarditis seven days prior to the development of symptoms via the variations in the heartbeat.
Paper structure
The remainder of the paper is organized as follows. In Sect. “Proposed Methodology”, the proposed model for autonomous diagnosis of myocarditis is presented in detail. Experimental results and discussions are presented in Sect. “Results and discussions”. Section “Conclusion” presents the conclusions of this study and the future directions.
Proposed methodology
This study constructed a model using deep learning to predict myocarditis cases, which uses ECG data as a diagnostic tool to achieve an automatic diagnosis of myocarditis. The most common ECG manifestations of myocarditis patients are shown in Table 1.
Table 1.
Abnormal ECG manifestations of patients with myocarditis
| Heart beat types | Heart beat phenomenon |
|---|---|
| Atrial fibrillation | Absence of sinus P waves and irregular RR intervals |
| Ventricular fibrillation | T-wave inversion |
| / | ST-segment elevation |
| / | PR-interval prolongation or shortening |
In this study, the myocarditis detection model includes three stages: preprocessing, feature extraction, and classification. Figure 1 depicts the conceptual layout of our suggested myocarditis diagnostic approach. First, the original signal’s noise is eliminated. Denoised ECG signals are used to obtain pure ECG signals. The heart rate variability (HRV) [48] signal is also retrieved concurrently from the denoised data. The ECG features and nonlinear features necessary for HRV signal analysis are then extracted using the IQGA. The properties of the collected ECG signals were then subjected to binary classification and multi-classification using an ADE-BPNN classifier to identify myocarditis.
Fig. 1.
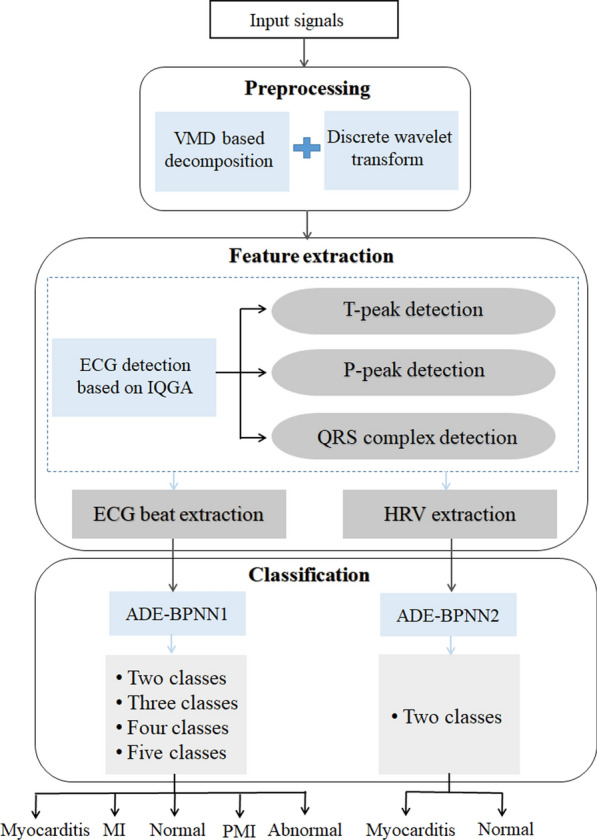
The block diagram of the proposed approach for myocarditis detection
Datasets
Training data sets
The Chinese PLA General Hospital (PLAGH) provided the training data for this paper, which was gathered by medical professors using a remote ECG diagnosis system. This information consists of ECG signal data from patients with myocarditis, normal ECGs, and other cardiac issues. 5200 instances of ECG signals were used in this study’s original data to create a detection model. The method employed was a fivefold cross-validation one. In each experiment, 20% of the learning data set is used as the validation set, while 80% of the data are chosen as the training set. In Table 2, the precise distribution is displayed.
Table 2.
Details of training and validation for different types of ECG
| Heart class | Number of available signals | Signals used in the proposed approach | Signals used in training | Signals used in validation |
|---|---|---|---|---|
| Myocarditis | 1200 | 1200 | 960 | 240 |
| Normal ECG | 1000 | 1000 | 800 | 200 |
| MI | 1200 | 1200 | 960 | 240 |
| Previous History of MI(PMI) | 1200 | 1200 | 960 | 240 |
| Abnormal ECG | 1000 | 1000 | 800 | 200 |
Testing data sets
The ClinicalTrials.gov database [49] and the ICIs-myocarditis database [50] are where the test results in this paper were obtained. ECGs from 147 myocarditis patients, including clinical ECG records from 125 individuals, were gathered and stored in the ClinicalTrials.gov database. They offered a three-day ECG. Two cardiologists conducted blind examinations and acquired data on twenty-four predetermined ECG characteristics. ECGs that solely displayed heart rhythm or prolonged ventricular arrhythmia were disregarded to assure the experiment’s correctness. ECGs from 319 myocarditis patients are available in the ICIs-myocarditis database. Each record in this database has 120 min of ECG data. Each record also has a 257 Hz sampling rate.
Preprocessing
The ECG is nonlinear, non-stationary, and vulnerable to noise pollution as a typical biological signal [36]. Electromyographical (EMG) interference is one of them and has a broad frequency range, making it spectrally aliased with the ECG [51]. To eliminate EMG interference, we used the technique of combining variational mode decomposition (VMD) and DWT which was suggested by researchers [46]. Although the researchers’ suggested denoising approaches have some general importance, they nevertheless have significant restrictions. The accuracy of VMD decomposition signals is directly impacted by the K number of decomposition layers in this process. In this study, the parameter K is optimized using multi-dimensional and multi-scale fuzzy entropy (MMFE), which may adaptively decide the parameter K to enhance the denoising performance of myocarditis-related ECG signals. Figure 2 displays the outcome of the myocarditis patient’s ECG signal’s denoising. The following are the steps for MMFE K value optimization:
Fig. 2.

Denoising of ECG signals of myocarditis patients
(a) The transformed M-point time series () by using VMD method to obtain the z-dimensional IMF. We assume that the number of IMFs in each sequence is , then the z-dimensional IMF can be expressed as (; );
(b) Calculating the preceding IMF function of each sequence. Among them, the sequence on the a-th scale can be expressed as:
| 1 |
where represents the convergence criterion.
(c) For the sequence of the -th scale on the M point, the MMFE values is calculated as follows.
| 2 |
| 3 |
| 4 |
where is the similarity between variables.
(d) Let the MMFE on the 1- scale be expressed as:
| 5 |
ECG signal feature extraction
The advantages of traditional ECG feature extraction techniques include a straightforward approach and low computational complexity. However, it is challenging to precisely pinpoint the feature point location due to the instability of the feature point locating algorithm. It is challenging to use the derived features in circumstances with extensive recognition applications. In order to extract the characteristics of the ECG beat and HRV signal, IQGA is used in this work.
Basic quantum genetic algorithm
The quantum genetic algorithm (QGA) [47] uses quantum logic gates to implement chromosome update operations, thereby achieving the optimal solution of the target, where chromosomes are represented by qubits. The state of a qubit can be expressed as:, Where and are the probability amplitudes of quantum bits, and the normalization condition is .Let & ,where represents the phase of the quantum bit. The adjustment operation of the quantum rotating gate u(t) is as follows.
| 6 |
where is the i-th quantum bit in the chromosome, is the rotation angle, and its size and rotation direction are determined according to the adjustment strategy designed in advance. Among them, where , is used to control the direction of the rotation angle, and is used to control the magnitude of the rotation angle.
Improved quantum genetic algorithm
The selection of QGA in this work can be explained by the fact that, despite its low feature extraction rate in earlier studies [47], it was employed for feature extraction of many different types of signals. In order to extract features from myocarditis ECG signals, IQGA is suggested. The quantum algorithm is subjected to mutation operations in this study using the Hadamard gate. To generate H qubits, the phase of the qubits is changed using a quantum Hadamard gate. The H gate uses the Hilbert space transformation to transform the space with and as base vectors into the space with and as base vectors. The states of the qubits are as follows.
| 7 |
The purpose of the quantum logic gate is to change the direction and angle of the rotation angle. The traditional angle encoding method uses quantum non-gate for mutation. Its rotation angle is , which is too large compared to Hadamard gate [52], as shown in Fig. 3. However, it ignores the optimal value. Therefore, the rotation angle after Hadamard gate conversion is to rotate the qubit clockwise by ,as shown in Fig. 4. The variation of the quantum qubit probability amplitude of the quantum Hadamard gate is as follows.
| 8 |
where is the gene bit in the quantum chromosome of .
Fig. 3.
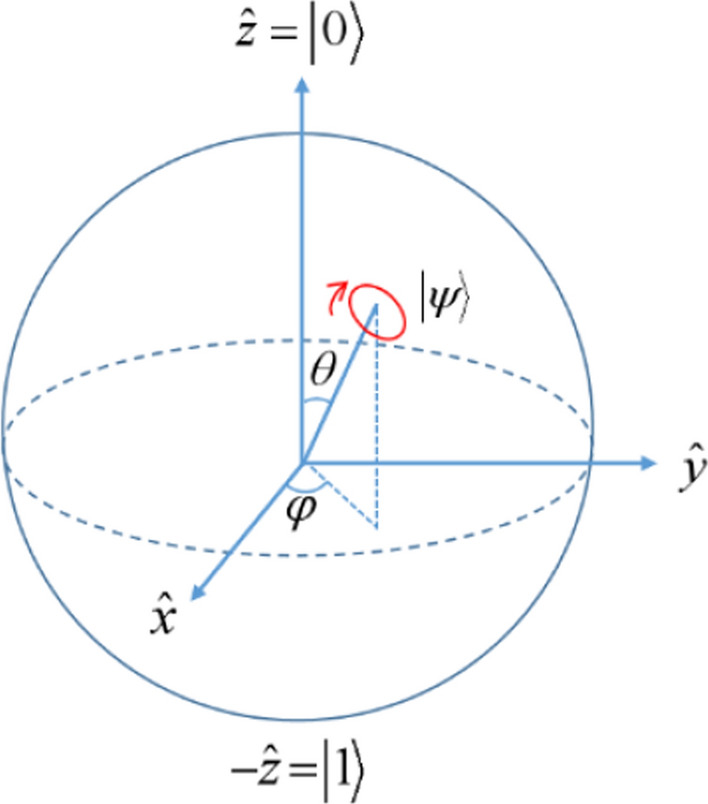
Bloch vector of quantum states
Fig. 4.
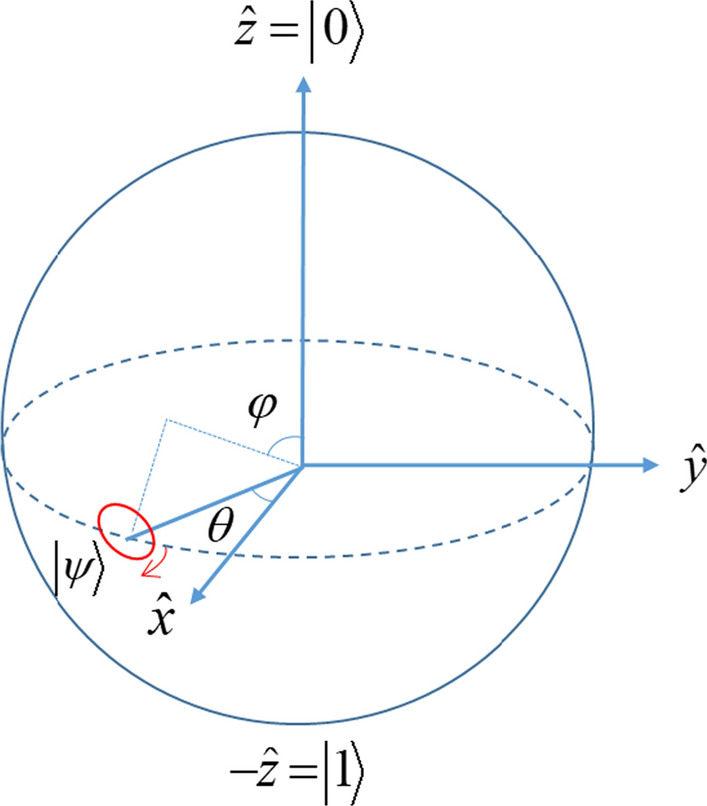
Improved Bloch vector of quantum states
Empirical adjustment techniques determine the size and direction of the rotation angle of traditional quantum revolving doors. After the rotation operation, the population search range is constrained by the magnitude of the rotation angle and will depend on convergence speed. The algorithm will prematurely converge if the rotation angle’s magnitude is too large. The algorithm’s rate of convergence will be slowed down if the rotation angle’s magnitude is too tiny. This paper proposes an approach to dynamically change the rotation angle based on the problems mentioned above.
| 9 |
where is the total number of iterations, is the current number of iterations, and is the incremental amplitude of the position and rotation angle obtained by iterating to times. is the rotation angle corresponding to the fitness of the searched optimal individual, and is the rotation angle corresponding to the fitness of the current individual. In formula (10), A is an adaptive change as the number of iterations changes, and the position of the next-generation optimal individual can be adjusted according to the current individual position of the -th generation. Advantages of this dynamic adjustment strategy: (a) The dynamic strategy is used to update the rotation angle, which can ensure the global convergence of the algorithm; (b) The corresponding rotation angle is selected according to the individual fitness value, which not only ensures the diversity of the group, but also ensures its convergence; (c) After each calculation of the rotation angle, the global and local optimal states of the population are combined with each other, and the search behavior contains random behavior. This can better avoid the disadvantage of falling into local optimum. Therefore, the of formula (9) can better adjust the direction of the population to search for the optimal individual in the next step.
The process of the IQGA is as follows:
Step 1: Population initialization. When the population is initialized, the population contains individuals, and its population is . Due to the randomness of the encoding when the population is initialized, the probability amplitude of the qubit is used as the encoding of the current position of the quantum. The encoding method of QGA is as follows.
| 10 |
where is the chromosome of the j-th individual of the t-th generation in the population, is the number of gene in the chromosome, and is the number of qubit encoding of each gene. Generally, all genes and are initialized to , which means that all states are superimposed with the same probability during the initial search. The corresponding binary codes are generated according to the probability amplitude of each individual. The measurement of individuals in the initial population can generate a random number in the interval [0,1], where each bit is either 0 or 1.Let , and are initialized.
Step 2: Quantum population is measured to obtain observed state .where , is a binary bit of 0 or 1.
Step 3: The fitness value of all individuals in the population is calculated, and the individual with the highest fitness value is selected as the evolutionary goal of the next generation.
Step 4: Let denote the maximum individual probability. If , . Otherwise, . If the condition is satisfied, the algorithm is terminated. Otherwise, step 5 is performed.
Step 5: The improved quantum rotation gate operation and Hadamard gate mutation operation are used to update to generate a new quantum population .And calculate the fitness of each individual in population and keep the best individual.
Step 6: If the number of iterations reaches the maximum value, then step 7 is performed. Otherwise, the genetic algebra iteration is t=t+1, and step 2 is performed.
Step 7: End the optimization process.
Fitness function
The ultimate goal of using the IQGA is to locate the extreme points in the wave group. The fitness function is as follows.
| 11 |
Among them, and are the positions of the ECG signal coordinates. If the result of the fitness value is larger, the search ability of the algorithm is better. Conversely, if the fitness is smaller, the ability to find wave points is worse, as shown in Fig. 5.
Fig. 5.
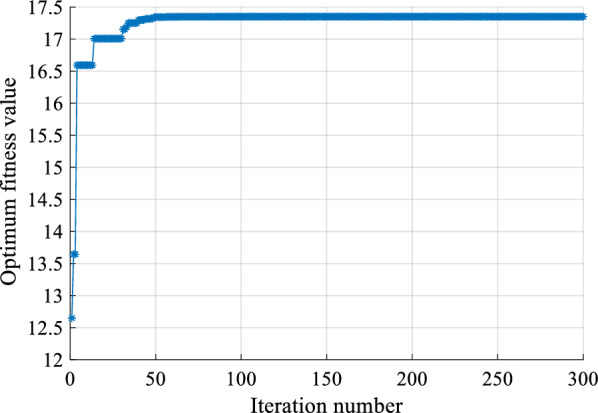
IQGA fitness curve
Implementation steps of feature extraction based on IQGA
Among the several characteristic waveforms of the ECG signal, the amplitude of the QRS complex is significantly higher than that of other waveforms [41] among which, the R-wave is the highest peak value of the ECG. We perform wave group detection on the preprocessed ECG data. First, IQGA is used to optimize the R-wave in this paper, and the global optimal solution is searched through the parallel processing of the algorithm to determine the detection of the R peak point. After determining the peak position of the R-wave, the peak detection of the Q-wave and S-wave is performed. Based on the detection information of the QRS wave, IQGA is used to detect the peak values of the P and T waves. At the same time, ECG characteristic parameters such as heart rate and R-R interval are calculated.
i. Detection of R-wave
We used IQGA for QRS complex detection. The detected maximum wave point value is R-point, and its minimum wave point value (negative extreme point) Q and S points.
ii. Detection of Q and S waves.
The detection of Q and S wave points is carried out based on the detection of R wave. The Q-wave is detected in a region before the R-wave peak, and the S-wave is detected in a region after the R-wave peak. The minimum point of QRS complex was found by IQGA. According to the slope of the minimum value (the slope is positive or negative) to determine the peak points of Q and S waves.
The specific steps for detecting Q-wave and S-wave are as follows.
Two negative extremum points are obtained through the detection of IQGA.
Connect the two negative value points with the peak point of R-wave respectively, which are two straight lines.
Find the slopes of these two line segments separately. If the slope is greater than zero, this point is the Q-wave point. Otherwise, this point is the S-wave point.
iii. Detection of P and T waves.
The detection of P waves and T waves is carried out on the basis of the peak positions of Q and S waves. First, the period of the R-R interval of the cardiac beat is calculated based on the detected R-wave. The period of the R-R interval is as follows.
| 12 |
where is the sampling point of the R-peak in the ECG signal. is the sampling frequency of the ECG signal.
P-wave detection is performed before the starting point of Q wave. If , take the RR-interval time 0.5 times before the Q-wave starting point as the detection interval. Otherwise, the time window before the starting position of each QRS complex wave is used as the detection interval of P-wave. Before calculating the absolute values of their differences from the amplitudes of the first three points at the Q-wave start location, we first used IQGA to determine the maximum and minimum values of the detection interval. The P-wave point is the minimum value point if the absolute value of the minimum value difference in the P-wave detection interval is greater than the absolute value of the maximum value difference of the wave point taken in the 1.2 times Q-wave area; otherwise, the P-wave point is the maximum value point. The P-wave point is searched using the largest value approach if the time difference between the P-wave point and the Q-wave’s starting point is less than 0.02 s. The T-wave peak point’s detection method is the same as the P-wave’s, hence it won’t be covered in detail here.
Feature extraction of ECG beat
The data used in this paper is used to extract the heart beat features in Table 1. However, redundant and irrelevant features in these data lead to problems in signal feature classification, which affects the accuracy of signal classification. Feature selection is to remove redundant and irrelevant features from the original dataset without changing the physical characteristics of the data. Assume that the extracted ECG features are . The feature types proposed from the ECG data set are shown in formulas (13)-(20).
| 13 |
| 14 |
| 15 |
| 16 |
| 17 |
| 18 |
| 19 |
| 20 |
where ,,,,,,, are the mean, median, maximum, minimum, variance, standard deviation, skewness, and kurtosis of the extracted feature , respectively.
Features extraction of HRV
In this Section, HRV analysis is performed on ECG signals according to formula (12). Its linear analysis and Poincare scatter diagram analysis [48] can reflect the autonomic nervous function of the heart. The linear analysis of HRV is a mathematical analysis based on the R-R interval. And the Poincare scatter diagram is a method of nonlinear analysis of HRV according to chaos theory. Therefore, we use mean (MEAN), the standard deviation of normal to normal (SDNN), mean standard deviation (SDANN), the root of mean square difference (RMSSD), coefficient of variation (CV) [53], Poincare scatter plot to analyze HRV, as shown in formula (21)–(25). They are the most significant indicators for the automatic analysis and diagnosis of myocarditis, which can predict the patient’s illness based on the HRV. The HRV of myocarditis patients is usually lower than that of ordinary people. The HRV signal is ready for the next-stage feature identification to assess cardiac condition information in normal subjects and myocarditis patients.
| 21 |
| 22 |
| 23 |
| 24 |
| 25 |
where is the value of the -th R-R interval. is the total number of R-R intervals recorded throughout. is the mean value of the R-R interval. is used to estimate the standard deviation of the R-R interval of 288 segments in 24 h. is the standard deviation of the mean R-R interval. is the root mean square of the difference between adjacent R-R intervals. is the coefficient of variation for comparing indicators with extensive differences in average.
ECG signal feature classification
This section proposes a signal classification model based on ADE-BPNN, which is a kind of supervised classification learning.
Basic differential evolution algorithm
The Differential Evolution (DE) algorithm is a heuristic random search algorithm based on population differences, which uses real vector encodings to randomly search in a continuous space to find an optimal solution [54]. It is a population-based adaptive global optimization algorithm that uses the operation process of mutation, crossover, and selection. The specific steps of the DE algorithm are as follows.
(1) Population initialization
To establish an initial point for the optimal search algorithm, first initialize the population. The initial population is chosen randomly from values within the given bound constraints. The initial population randomly generated is as follows.
| 26 |
where is the initial population structure vector, is the individual dimension of the population, is the population size, and are the upper and lower bound of individual vectors in the population, respectively, and is a random matrix with rows and columns.
(2) Mutation operation
The expression for the variation among individuals in a population is as follows.
| 27 |
where is the position label in the -th generation population (), ,, and are randomly selected serial-numbers respectively, is a mutation operator that usually range in the interval [0,2].
(3) Cross operation
In order to increase population diversity, the target vector individual in the -generation population is crossed with the partial genes of its mutation vector individual to generate the experimental vector individual , and its expression is as follows.
| 28 |
where rand(1) is a uniformly distributed random number and its value range in the interval [0,1], is the crossover probability constant and its value range in the interval [0,1], is the index of the randomly chosen dimensional variable, and is the -th variable gene of the -th individual.
(4) Selection operation
The test vector individual is compared with the target vector individual in the current population to determine whether the experimental vector will enter the next generation. If the fitness of the test vector individual is better than that of , that individual will be selected as the offspring. Otherwise, will be selected as the offspring. Its selection operation can be expressed as follows.
| 29 |
where is the individual fitness function.
Adaptive mutation strategy of differential evolution algorithm
Like other evolutionary algorithms, the DE algorithm has certain limitations. The mutation factor determines the magnification of the deviation vector. If the mutation factor is too large, the accuracy of finding the global optimal solution is low. If the mutation factor is too small, the diversity of the population cannot be guaranteed. The DE algorithm is prone to premature phenomenon. Therefore, an adaptive mutation factor is introduced in the mutation operation. So that the mutation rate will gradually decrease with the increase of the number of iterations. In this way, a larger variation factor in the early stage can ensure the diversity of the population, and a smaller variation factor in the later stage can retain excellent individuals. The expression of the adaptive mutation factor is as follows.
| 30 |
where is the initial value of the mutation operator, is the current evolutionary algebra, and is the maximum evolutionary algebra.
ECG signal feature classification by ADE-BPNN
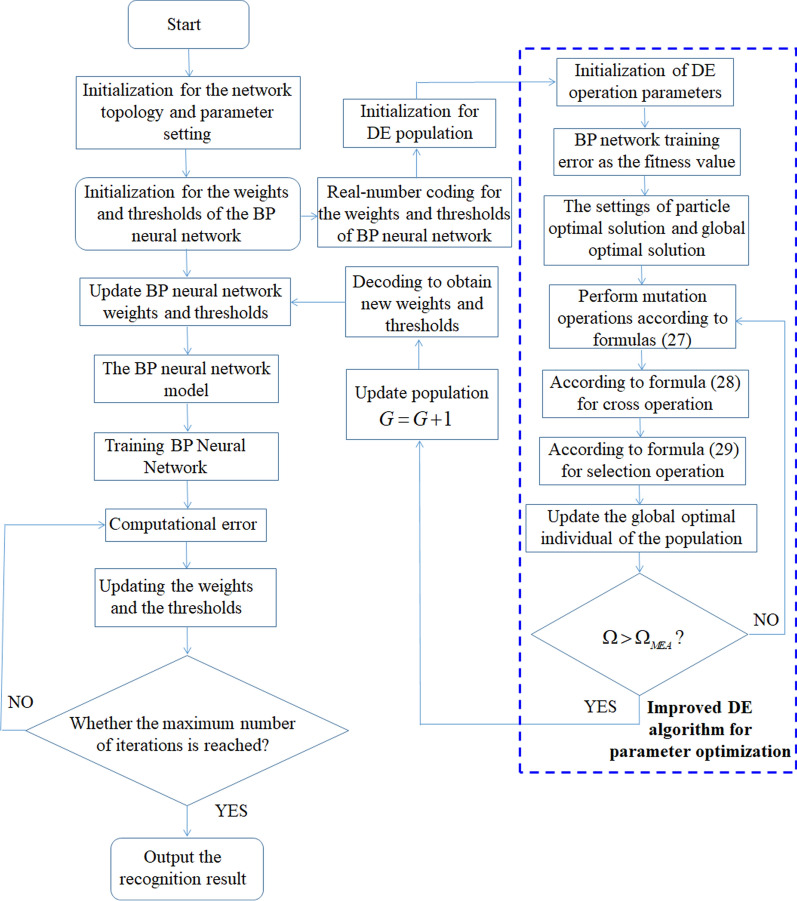
In this paper, the ADE-BPNN algorithm is used to classify the extracted ECG signal features. Aiming at the shortcomings of BPNN’s slow convergence speed and easy fall into local extremum. Using the ADE algorithm to optimize the weight and threshold of BPNN, the multi-classification and binary classification models are established. The flow chart of the ADE-BPNN algorithm is shown in Fig. 6.
Fig. 6.
Flow chart of recognition and classification of ADE-BPNN
Results and discussions
The setting of the experimental parameters
In the IQGA proposed in this paper, the population size is 200, the chromosome length is 30, the quantum number of chromosomes is 10, the crossover probability is 0.8, the mutation probability is 0.01, and the number of iterations is 300.
The ADE-BPNN parameters are set as follows: the population size is 70, the maximum crossover factor is 0.9, and the minimum crossover factor is 0.3. The maximum training time is 200, the training error target is 0.02, and the learning rate is 0.001.
The setting of the experimental environment
The hardware environment is powered by an AMD Ryzen 7 PRO 4750U with Radeon Graphics 1.70 GHz. The software environment is compiled using Windows 10 operating system and MATLAB R2019b software package.
Evaluation Index
The proposed myocarditis classification model is evaluated by sensitivity (Sen), specificity (Spe), F-measure (F-mea), accuracy (ACC), receiver operating characteristic (ROC) curves, and Matthew correlation coefficient (MCC) in this paper. The performance metrics represented by Eqs. (31)–(35) [55] are as follows.
| 31 |
| 32 |
| 33 |
| 34 |
| 35 |
where , , , are the number of correctly classified samples, unclassified samples, falsely classified samples and correctly unclassified samples, respectively.
Analysis of the feature extraction
Feature extraction using IQGA
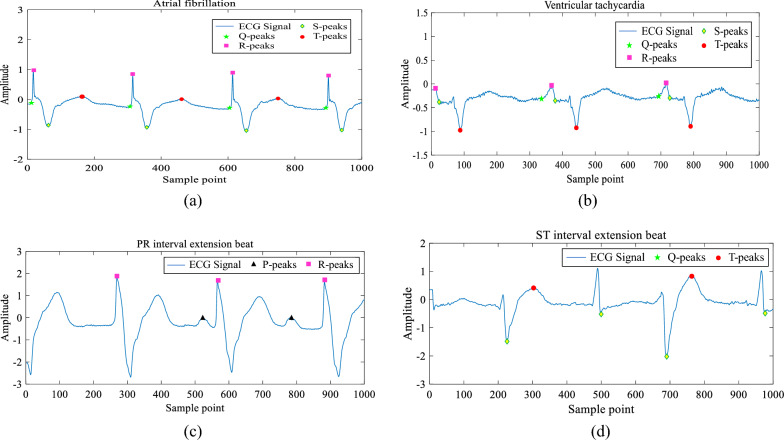
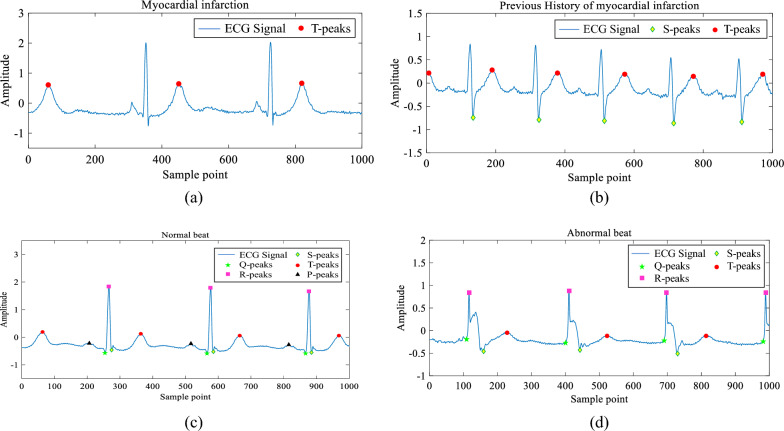
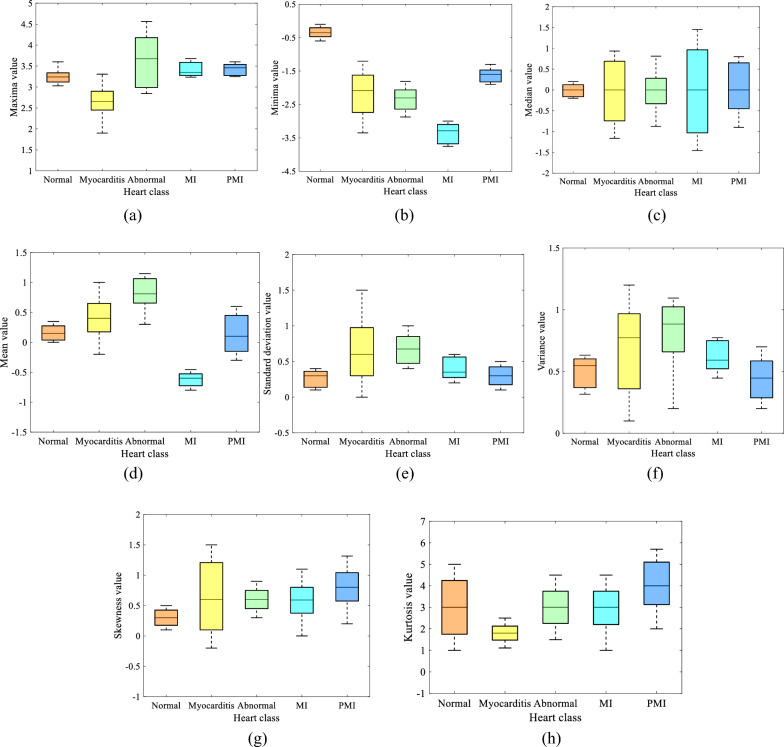
In this study, we choose IQGA to extract the main features of ECG signals. Figure 7 shows five signal features extracted from the ECG signals of patients with myocarditis (see Table 1 for the ECG characteristics of myocarditis), which are used to detect patients with myocarditis. The features extracted from other ECG signals (including MI, PMI, Normal Heartbeats and Abnormal Heartbeats) are shown in Fig. 8. We carry out data statistical feature extraction using feature values proposed in ECG data. The statistical characteristics of ECG and other heart rhythms of myocarditis patients are shown in Fig. 9.
Fig. 7.
Five signal features extracted from myocarditis patients: a Atrial fibrillation, b Ventricular fibrillation, c PR interval extension beat, d ST interval extension beat
Fig. 8.
Features extracted from other ECG signals: a MI, b PMI, c Normal Heartbeat, d Abnormal Heartbeat
Fig. 9.
Statistical characteristics of ECG and other cardiac rhythms of myocarditis patients: a Maxima value, b Minima value, c Median value, d Mean value, e Standard deviation value, f Variance value, g Skewness value, h Kurtosis value
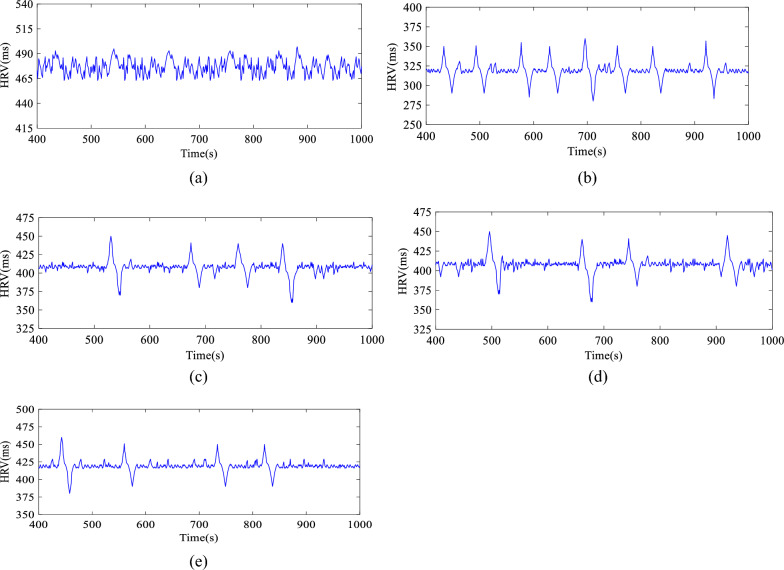
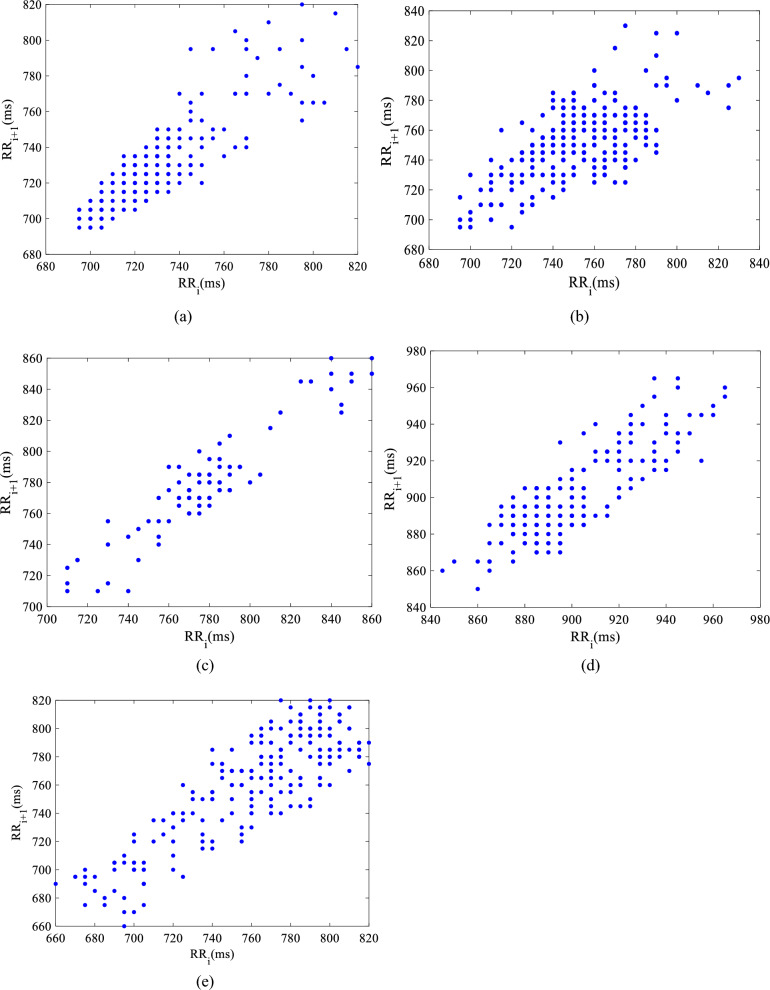
In order to better diagnose patients infected with myocarditis, this paper uses HRV analysis to detect cardiac activity. The HRV of myocarditis and other ECGs are shown in Fig. 10. It can be seen from Fig. 10 that the HRV signals of normal heart rate and arrhythmia both present nonlinear changes. The HRV of a normal heart rhythm does not vary much and is relatively regular. The HRV fluctuation of arrhythmia is relatively large. The HRV linear analysis for myocarditis and other ECGs is shown in Table 3, in which the HRV changes of myocarditis patients are more severe than those of other ECGs. Figure 11 shows the Poincare scatter plots of various types of HRV, and each of the five scatter plots has its typical graphic features. The Poincare scatter plot of ordinary people is in the shape of a comet, its area is small, and the scattered points are very concentrated. The Poincare scatter plots of MI, PMI, and abnormal persons are in the shape of a thick rod, and their scatter area is greater than that of a comet. However, the scatter diagram of myocarditis presents an irregular shape with high divergence, which is quite different from other ECG signals. Its area is the largest in these scatterplots. As can be seen, the HRV of myocarditis is significantly different from other ECGs.
Fig. 10.
HRV changes of different types of ECG signals: a Normal heartbeat, b Myocarditis, c MI, d PMI, e Abnormal heartbeat
Table 3.
HRV linear analysis for myocarditis and other ECGs
| Heart type | Mean (ms) | SDNN (ms) | SDANN (ms) | RMSSD (ms) | CVRR |
|---|---|---|---|---|---|
| Myocarditis | 661.50 | 11.49 | 150.74 | 8.05 | 0.227 |
| Normal heartbeats | 770.53 | 145.64 | 110.97 | 27.13 | 0.144 |
| MI | 755.43 | 25.09 | 126.30 | 21.29 | 0.167 |
| PMI | 749.80 | 24.78 | 124.09 | 20.95 | 0.165 |
| Abnormal heartbeats | 729.44 | 19.90 | 135.60 | 11.41 | 0.186 |
Fig. 11.
Poincare scatter plot performance of different types of ECG signals: a Normal heartbeat, b Myocarditis, c Abnormal heartbeat, d MI, e PMI
Performance analysis of the IQGA
In order to verify the performance of the algorithm, IQGA is compared with traditional feature extraction methods through different databases. Traditional methods mainly include Particle Swarm Optimization (PSO) algorithm, Multi-population quantum genetic algorithm (MPQGA), and Ant Colony Algorithm (ACA)-genetic algorithm (GA).
As shown in Table 4, Stochastic methods (ACA and PSO algorithm) can obtain the global optimal solution, but their operation takes a long time and the space utilization rate is low. Although the two methods of QGA and ACA-GA have strong versatility, their randomness also brings a certain time cost. Compared with traditional algorithms, IQGA has low time complexity and a large application space.
Table 4.
Comparison of the performances of different feature extraction algorithms
| Databases | Methods | Execution time/s | Space utilization rate/% |
|---|---|---|---|
| Actual collection data in the PLAGH | PSO | 102.40 | 59.20 |
| ACA | 109.08 | 60.73 | |
| QGA | 80.69 | 74.19 | |
| ACA-GA | 77.35 | 75.60 | |
| IQGA | 45.22 | 87.52 | |
| Clinical trials.gov database | PSO | 105.64 | 56.33 |
| ACA | 103.50 | 54.09 | |
| QGA | 87.01 | 77.10 | |
| ACA-GA | 89.24 | 74.31 | |
| IQGA | 47.80 | 86.92 | |
| ICIs-myocarditis database | PSO | 103.19 | 58.00 |
| ACA | 108.25 | 58.42 | |
| QGA | 79.11 | 78.21 | |
| ACA-GA | 81.03 | 77.54 | |
| IQGA | 45.96 | 87. 90 |
Analysis of the feature classification
We adopted this paper to diagnose myocarditis by using ADE-BPNN to perform binary and multi-class classification of various types of ECG signals. We used four different classification schemes for evaluation: two classes (Myocarditis vs. Normal, Myocarditis vs. Abnormal, Myocarditis vs. MI, and Myocarditis vs. PMI), three classes (Myocarditis vs. Abnormal vs. MI, Myocarditis vs. Abnormal vs. PMI), four classes (Myocarditis vs. Abnormal vs. MI vs. PMI), and five classes (Myocarditis vs. Normal vs. Abnormal vs. MI vs. PMI). In this study, the proposed ADE-BPNN was used to conduct multiple independent experiments on the above four schemes, and compared with Random Forest (RF) [56], SVM [25], CNN [27], and BPNN [57].
First, the performance of our classifier is evaluated. The extracted feature vectors were input into BPNN optimized by ADE. The training procedure of ADE-BPNN is shown in Fig. 12. It can be seen from Fig. 12 that the training error of ADE-BPNN reaches the target accuracy after 125 trainings, and the convergence accuracy is 0.0095. The error value of ADE-BPNN decreased by 0.0031 compared with BPNN.
Fig. 12.
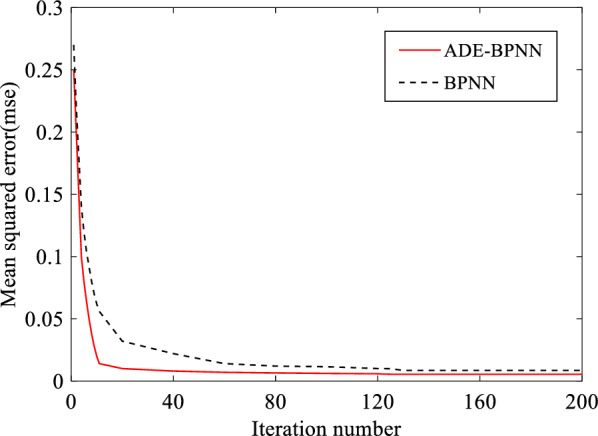
Comparison of the error drop curves of the network
Performance analysis of binary classification
For binary classification, four classification tasks (Myocarditis vs. Normal, Myocarditis vs. Abnormal, Myocarditis vs. MI, and Myocarditis vs. PMI) are performed. The ROC curve results of the four tasks are shown in Fig. 13. The area under the ROC curve (AUC) values of ADE-BPNN in the four classification tasks increased by 1.72%, 2.15%, 2.2%, and 1.78%, respectively. It can be seen that the ROC curve of ADE-BPNN has a higher AUC value than other classifiers. Table 5 shows the comparison of classification performance for binary classification. The sensitivity, specificity, accuracy, F-measure, and MCC of the proposed method for Myocarditis vs. Normal increased by 1.33%, 0.75%, 1.64%, 1.25%, and 0.55%, respectively. The sensitivity, specificity, accuracy, F-measure, and MCC of the proposed method for Myocarditis vs. Abnormal increased by 1.63%, 1.15%, 0.74%, 1.26%, and 0.95%, respectively. The sensitivity, specificity, accuracy, F-measure, and MCC of the proposed method for Myocarditis vs. MI increased by 0.56%, 0.88%, 1.74%, 0.83%, and 1.17%, respectively. The sensitivity, specificity, accuracy, F-measure, and MCC of the proposed method for Myocarditis vs. PMI increased by 1.57%, 1.19%, 0.50%, 0.45%, and 0.74%, respectively.
Fig. 13.
The ROC curve results of the four tasks: a Myocarditis vs. Normal, b Myocarditis vs. Abnormal, c Myocarditis vs. MI, d Myocarditis vs. PMI
Table 5.
The comparison of classification performance for binary classification
| Method | Sen | Spe | Acc | MCC | F-me |
|---|---|---|---|---|---|
| Myocarditis vs. Normal | |||||
| RF | 0.9690 | 0.9618 | 0.9700 | 0.9638 | 0.9706 |
| SVM | 0.9711 | 0.9670 | 0.9687 | 0.9769 | 0.9751 |
| CNN | 0.9673 | 0.9724 | 0.9759 | 0.9728 | 0.9669 |
| BPNN | 0.9795 | 0.9835 | 0.9790 | 0.9885 | 0.9857 |
| ADE-BPNN | 0.9927 | 0.9910 | 0.9954 | 0.9940 | 0.9982 |
| Myocarditis vs. Abnormal | |||||
| RF | 0.9589 | 0.9608 | 0.9697 | 0.9583 | 0.9625 |
| SVM | 0.9657 | 0.9681 | 0.9698 | 0.9667 | 0.9703 |
| CNN | 0.9692 | 0.9755 | 0.9730 | 0.9732 | 0.9649 |
| BPNN | 0.9738 | 0.9809 | 0.9883 | 0.9798 | 0.9720 |
| ADE-BPNN | 0.9899 | 0.9923 | 0.9957 | 0.9892 | 0.9844 |
| Myocarditis vs. MI | |||||
| RF | 0.9557 | 0.9539 | 0.9574 | 0.9689 | 0.9560 |
| SVM | 0.9684 | 0.9620 | 0.9799 | 0.9759 | 0.9669 |
| CNN | 0.9780 | 0.9724 | 0.9751 | 0.9805 | 0.9733 |
| BPNN | 0.9796 | 0.9813 | 0.9754 | 0.9821 | 0.9794 |
| ADE-BPNN | 0.9851 | 0.9900 | 0.9936 | 0.9937 | 0.9876 |
| Myocarditis vs. PMI | |||||
| RF | 0.9602 | 0.9517 | 0.9631 | 0.9590 | 0.9576 |
| SVM | 0.9631 | 0.9589 | 0.9718 | 0.9628 | 0.9653 |
| CNN | 0.9755 | 0.9692 | 0.9756 | 0.9771 | 0.9718 |
| BPNN | 0.9719 | 0.9750 | 0.9890 | 0.9836 | 0.9783 |
| ADE-BPNN | 0.9875 | 0.9867 | 0.9940 | 0.9909 | 0.9827 |
It can be seen from Table 5 that the improved classification algorithm in this paper has the best performance in terms of various evaluation indicators in the comparison between myocarditis and different types of ECG.
Performance analysis of multi-class classification
For multi-class classification, this section studies three categories of classification (Myocarditis vs. Abnormal vs. MI, Myocarditis vs. Abnormal vs. PMI), four categories of classification (Myocarditis vs. Abnormal vs. MI vs. PMI), and five categories of classification (Myocarditis vs. Normal vs. Abnormal vs. MI vs. PMI).
In three categories classification, the ROC curve of three categories classification after classification by different classifiers is shown in Fig. 14. The AUC values of ADE-BPNN in Myocarditis vs. Abnormal vs. MI and Myocarditis vs. Abnormal vs. PMI increased by 2.2% and 1.9%, respectively. Table 6 shows the comparison of classification performance for three categories classification. The sensitivity, specificity, accuracy, F-measure, and MCC of the proposed method for Myocarditis vs. Abnormal vs. MI increased by 0.87%, 1.9%, 1.27%, 0.97%, and 1.03%, respectively. The sensitivity, specificity, accuracy, F-measure, and MCC of the proposed method for Myocarditis vs. Abnormal vs. PMI increased by 1.14%, 1.29%, 0.70%, 1.36%, and 1.33%, respectively. It can be seen from Fig. 14 and Table 6 that the classification effect of ADE-BPNN is better than other classifiers for the three categories classifications.
Fig. 14.
The ROC curve of three categories classification after classification by different classifiers:a Myocarditis vs. Abnormal vs. MI, b Myocarditis vs. Abnormal vs. PMI
Table 6.
The comparison of classification performance for three categories classification
| Method | Sen | Spe | Acc | MCC | F-me |
|---|---|---|---|---|---|
| Myocarditis vs. Abnormal vs. MI | |||||
| RF | 0.9442 | 0.9466 | 0.9569 | 0.9585 | 0.9490 |
| SVM | 0.9491 | 0.9528 | 0.9622 | 0.9683 | 0.9577 |
| CNN | 0.9592 | 0.9540 | 0.9776 | 0.9690 | 0.9609 |
| BPNN | 0.9730 | 0.9697 | 0.9764 | 0.9751 | 0.9734 |
| ADE-BPNN | 0.9815 | 0.9886 | 0.9990 | 0.9852 | 0.9829 |
| Myocarditis vs. Abnormal vs. PMI | |||||
| RF | 0.9480 | 0.9573 | 0.9490 | 0.9522 | 0.9505 |
| SVM | 0.9572 | 0.9619 | 0.9524 | 0.9637 | 0.9572 |
| CNN | 0.9618 | 0.9687 | 0.9759 | 0.9694 | 0.9668 |
| BPNN | 0.9750 | 0.9728 | 0.9793 | 0.9715 | 0.9700 |
| ADE-BPNN | 0.9862 | 0.9855 | 0.9962 | 0.9846 | 0.9834 |
In the four categories classification used to diagnose myocarditis, the ROC curve of four categories classification after classification by different classifiers is shown in Fig. 15. It can be seen that the AUC value of ADE-BPNN in the four categories classification increased by 0.35%. Table 7 shows the comparison of classification performance for four categories classification. Compared with other algorithms, our myocarditis detection algorithm can improve the sensitivity, specificity, accuracy, F-measure, and MCC by 0.52%, 1.38%, 1%, 1.05%, and 0.77%, respectively. It can be seen from Fig. 15 and Table 7 that the algorithm has a high classification performance.
Fig. 15.

ROC curve of four categories classification after classification by different classifiers
Table 7.
The comparison of classification performance for four categories classification
| Method | Sen | Spe | Acc | MCC | F-me |
|---|---|---|---|---|---|
| Myocarditis vs. Abnormal vs. MI vs. PMI | |||||
| RF | 0.9428 | 0.9441 | 0.9482 | 0.9507 | 0.9518 |
| SVM | 0.9491 | 0.9497 | 0.9515 | 0.9642 | 0.9604 |
| CNN | 0.9637 | 0.9563 | 0.9627 | 0.9665 | 0.9629 |
| BPNN | 0.9799 | 0.9672 | 0.9784 | 0.9790 | 0.9697 |
| ADE-BPNN | 0.9892 | 0.9907 | 0.9983 | 0.9866 | 0.9800 |
In the five categories classification, the ROC curve obtained after feature classification is shown in Fig. 16. The results contained in Fig. 16 show that the AUC value of ADE-BPNN in the five categories classification reaches 0.9879, which is 1.31% higher than the traditional algorithm. The comparison of classification performance for five categories classification is shown in Table 8. The sensitivity, specificity, accuracy, F-measure, and MCC of the proposed method for five categories of classification increased by 0.83%, 1.15%, 1.27%, 0.50%, and 1.66%, respectively. It can be seen from Fig. 16 and Table 8 that the classification effect of ADE-BPNN is better than other classifiers for the five categories classifications.
Fig. 16.
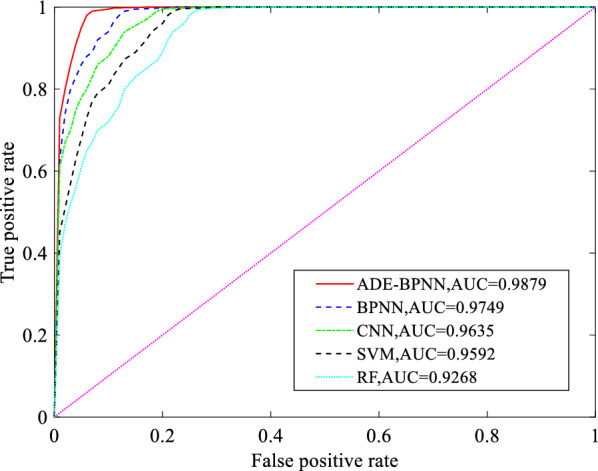
ROC curve of five categories classification after classification by different classifiers
Table 8.
The comparison of classification performance for five categories classification
| Method | Sen | Spe | Acc | MCC | F-me |
|---|---|---|---|---|---|
| Myocarditis vs. Normal vs. Abnormal vs. MI vs. PMI | |||||
| RF | 0.9491 | 0.9504 | 0.9592 | 0.9451 | 0.9500 |
| SVM | 0.9528 | 0.9587 | 0.9481 | 0.9610 | 0.9576 |
| CNN | 0.9659 | 0.9623 | 0.9535 | 0.9579 | 0.9635 |
| BPNN | 0.9763 | 0.9682 | 0.9770 | 0.9726 | 0.9748 |
| ADE-BPNN | 0.9945 | 0.9895 | 0.9959 | 0.9890 | 0.9793 |
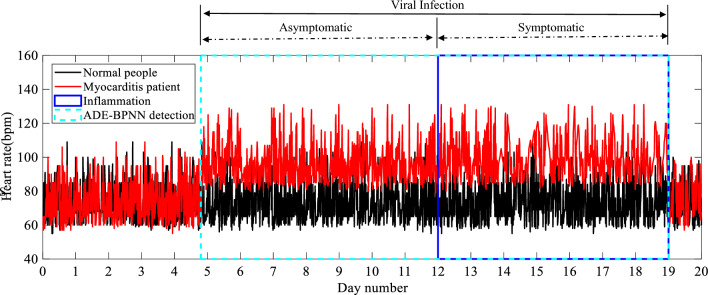
ADE-BPNN-Based HRV for myocarditis diagnosis
In order to further illustrate the effectiveness and robustness of the proposed classification model. In this Section, we collected twenty days ECG recordings from patients with myocarditis and normal person. And then identify the HRV of the two ECG signals by ADE-BPNN. Figure 17 shows the myocarditis prediction of HRV based on ADE-BPNN. As can be seen, the heart rate of myocarditis patients undergoes drastic changes during infection with the virus. The infection period of the virus can be detected by ADE-BPNN, and it can be detected seven days before the symptoms of the patient. This method of detecting heartbeat can quickly and reliably screen out patients with myocarditis in advance to prevent infection of other healthy people (See Fig. 17).
Fig. 17.
Myocarditis Diagnosis of HRV Based on ADE-BPNN
Performance analysis of classification algorithm based on ADE-BPNN
In order to further verify the effectiveness of the proposed classifier, ECG signals from the Actual collection data in the hospital, ClinicalTrials.gov database, and ICIs-myocarditis database were used for testing. As can be seen from Table 9, compared to the classification algorithms of RF, SVM, CNN, and BPNN, the proposed ADE-BPNN algorithm demonstrates notable improvements in average accuracy across different datasets. In the Actual collection data, the ADE-BPNN algorithm achieved an increase of 4.03%, 3.94%, 2.97%, and 1.61%, respectively. In the ClinicalTrials.gov database, the ADE-BPNN algorithm showed an increase of 5.18%, 3.97%, 2.41%, and 1.65%, respectively. In the ICIs-myocarditis database, the ADE-BPNN algorithm yielded an increase of 3.97%, 3.55%, 1.29%, and 1.72%, respectively.
Table 9.
Comparison of the performances of different classification algorithms
| Databases | Methods | Acc | Execution time/s | Space utilization rate/% |
|---|---|---|---|---|
| Actual collection data in the PLAGH | RF | 0.9564 | 120.59 | 65.28 |
| SVM | 0.9573 | 125.80 | 78.11 | |
| CNN | 0.9670 | 100.79 | 76.33 | |
| BPNN | 0.9806 | 95.00 | 76.00 | |
| ADE-BPNN | 0.9967 | 60.38 | 90.98 | |
| ClinicalTrials.gov database | RF | 0.9423 | 126.00 | 68.50 |
| SVM | 0.9544 | 131.92 | 75.81 | |
| CNN | 0.9700 | 98.79 | 77.02 | |
| BPNN | 0.9776 | 93.60 | 75.89 | |
| ADE-BPNN | 0.9941 | 57.14 | 88.30 | |
| ICIs-myocarditis database | RF | 0.9557 | 117.24 | 66.74 |
| SVM | 0.9609 | 120.81 | 76.95 | |
| CNN | 0.9835 | 102.05 | 77.30 | |
| BPNN | 0.9792 | 95.49 | 76.52 | |
| ADE-BPNN | 0.9964 | 59.02 | 90.18 |
After the RF algorithm introduces randomness, the model is not easy to fall into overfitting. When the number of decision trees in RF is large, the space and time required for training will be relatively large. SVM uses a subset of the training set to improve memory utilization. SVM uses a subset of the training set to improve memory utilization. However, SVM is sensitive to parameters and has high computational complexity, which increases the running time of the algorithm. CNNs are effective for detection on relatively large datasets. But the algorithm requires a lot of computing resources, and it will consume a lot of time when training and using it. BPNN has the ability to approximate arbitrary nonlinear mappings through learning. But it is very sensitive to the initial weight, and it is easy to converge to a local minimum. And it may have problems such as gradient disappearance or gradient explosion when dealing with large-scale data, which will cause the training process to become very slow. ADE-BPNN uses the ADE algorithm to optimize the weights and thresholds of BPNN and then establishes binary and multi-class models.
From Table 9, it can be observed that the ADE-BPNN algorithm greatly reduces the complexity of calculation, shortens the operation time, and solves the problem of excessive space occupation. In summary, the proposed classification algorithm in this paper has a high detection rate, high space utilization, and extremely short running time (Table 9).
Comparison of the results with related studies
Reference [58] demonstrated that patients with myocarditis can be diagnosed by fragmented QRS (fQRS). At the same time, the diagnostic rate of fQRS in patients with myocarditis can also be evaluated. However, the existence of fQRS is only a simple clinical diagnostic tool. In patients with related heart disease (myocardial ischemia, myocardial infarction, or myocardial scarring), fQRS waves are present in the ECG signal. Myocarditis diagnosed by fQRS has no definitive history, and there is no serial comparison of ECG. In this study, patients with myocarditis were diagnosed by using deep learning to detect abnormal areas of ECG signals. In addition, many scholars have applied research based on deep learning to the diagnosis of cardiomyopathy-oriented diseases. Among them, many studies have achieved good classification accuracy for ECG classification of myocardial infarction. Reference [33] achieved a recognition rate of 93.61%. Reference [34] achieved a recognition rate of 96%. Reference [35] proposed two different classification methods, and their recognition rates were 98.69% and 98.84%, respectively. Reference [37] achieved a recognition rate of 93.53%. Reference [38] achieved a recognition rate of 92.4%. Reference [39] has a recognition rate of 99.31% in the binary classification of MI and nonMI. Reference [41] achieved a recognition rate of 99.06%. Reference [36] achieved a recognition rate of 99.06%. Reference [40] achieved a recognition rate of 95.49%. Compared with the above references, our proposed deep learning-based diagnosis method for myocarditis has an efficient classification ability.
Conclusion
In this study, we propose a new ECG-based method for the automatic detection of myocarditis. By distinguishing the ECG of myocarditis patients from different types of ECG, it can detect myocarditis patients efficiently. The main features of the ECG beat signal and HRV signal is extracted by an improved quantum genetic algorithm. The extracted features are classified by ADE-BPNN to detect myocarditis patients. In addition, five-fold cross-validation was used to evaluate the reliability of the proposed model. Compared with the existing myocarditis detection system based on ECG signals, the method proposed in this paper has higher detection accuracy for the diagnosis of myocarditis. At the same time, as a new myocarditis diagnostic tool, ADE-BPNN can effectively detect viral myocarditis. Detecting myocarditis disease before symptoms appear during the infectious period can reduce the extent of damage to the heart.
Future work includes: (I) the proposed autonomous algorithm of myocarditis is connected with a dynamic cloud system to help medical staff complete remote diagnosis on mobile devices or computers. Through the calculation of the diagnostic model, a large amount of remote ECG data can be screened out to compare features with a high degree of complexity. Then the electrocardiogram is automatically diagnosed; (II) the features of the ECG signal extracted in this paper are all time-domain features. Subsequent research will extract frequency-domain features, such as power spectral density, Fourier transform, and fractal dimension. It is used to analyze the complexity and chaos of ECG signals.
Acknowledgements
This research was supported by Beijing Natural Science Foundation(M21018) and Hainan Province Science and Technology Special Fund (ZDYF2021GXJS205).
Authors contributions
LW undertook conceptualization, methodology and original draft writing. SG designed the study during the process of proposal development. LH handled the data collection process. XS was responsible for the experiments of the specific technical indicators in the article. ZZ contributed to the analysis of the data. ABC revised the manuscript. All authors read and approved the final manuscript.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Declarations
Conflict of interest
All authors read and approved the final manuscript. The authors declare that they have no competing interests.
Ethical approval
This article does not contain any data, or other information from studies or experimentation, with the involvement of human or animal subjects.
Informed consent
Informed consent was obtained from all individual participants included in the study.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Lei Wu and Shuli Guo have contributed equally to this work.
References
- 1.Tschöpe C, et al. Myocarditis and inflammatory cardiomyopathy: current evidence and future directions. Nat Rev Cardiol. 2021;18(3):169–193. doi: 10.1038/s41569-020-00435-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nishiga M, et al. COVID-19 and cardiovascular disease: from basic mechanisms to clinical perspectives. Nat Rev Cardiol. 2020;17(9):543–558. doi: 10.1038/s41569-020-0413-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Huang X, et al. Age-associated changes in adverse events arising from anti-PD-(L) 1 therapy. Front Oncol. 2021;11:619385. doi: 10.3389/fonc.2021.619385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Italia L, et al. COVID-19 and heart failure: from epidemiology during the pandemic to myocardial injury, myocarditis, and heart failure sequelae. Front Cardiovasc Med. 2021;8:713560. doi: 10.3389/fcvm.2021.713560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shiyovich A, et al. Myocarditis following COVID-19 vaccination: magnetic resonance imaging study. Eur Heart J Cardiovasc Imaging. 2022;23(8):1075–1082. doi: 10.1093/ehjci/jeab230. [DOI] [PubMed] [Google Scholar]
- 6.Strain T, et al. Wearable-device-measured physical activity and future health risk. Nat Med. 2020;26(9):1385–1391. doi: 10.1038/s41591-020-1012-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Song W, et al. Electrocardiographic features of immune checkpoint inhibitor-associated myocarditis. Curr Probl Cardiol. 2022;48:101478. doi: 10.1016/j.cpcardiol.2022.101478. [DOI] [PubMed] [Google Scholar]
- 8.Tse Y-H, et al. Lenalidomide-induced focal myocarditis mimicking acute ST segment elevation myocardial infarction. Postgraduate Med J. 2021;97(1154):762–763. doi: 10.1136/postgradmedj-2020-139107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Svensson A, et al. Arrhythmogenic right ventricular cardiomyopathy-evolution of electrocardiographic markers during long-term follow-up prior to ascertainment of diagnosis. Eur Heart J. 2022;43(Supplement_2):544–1754. [Google Scholar]
- 10.Mirahmadizadeh A, et al. The relationship between demographic features, anthropometric parameters, sleep duration, and physical activity with ECG parameters in Fasa Persian cohort study. BMC Cardiovasc Disord. 2021;21(1):1–11. doi: 10.1186/s12872-021-02394-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jin Y, et al. A novel attentional deep neural network-based assessment method for ECG quality. Biomed Signal Process Control. 2023;79:104064. [Google Scholar]
- 12.Greener JG, et al. A guide to machine learning for biologists. Nat Rev Mol Cell Biol. 2022;23(1):40–55. doi: 10.1038/s41580-021-00407-0. [DOI] [PubMed] [Google Scholar]
- 13.LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 14.Sai YP, Rajaniumari LV. Cognitive assistant DeepNet model for detection of cardiac arrhythmia. Biomed Signal Process Control. 2022;71:103221. [Google Scholar]
- 15.Ranjan R, Bikash CS, Bhandari AK. Cardiac artifact noise removal from sleep eeg signals using hybrid denoising model. IEEE Trans Instrum Measure. 2022;71:1–10. [Google Scholar]
- 16.Sadiq MT, et al. Motor imagery BCI classification based on novel two-dimensional modelling in empirical wavelet transform. Electron Lett. 2020;56(25):1367–1369. [Google Scholar]
- 17.Sadiq MT, et al. Motor imagery EEG signals decoding by multivariate empirical wavelet transform-based framework for robust brain–computer interfaces. IEEE Access. 2019;7:171431–171451. [Google Scholar]
- 18.Merah M, Abdelmalik TA, Larbi BH. R-peaks detection based on stationary wavelet transform. Comput Methods Prog Biomed. 2015;121(3):149–160. doi: 10.1016/j.cmpb.2015.06.003. [DOI] [PubMed] [Google Scholar]
- 19.Akbari H, et al. Recognizing seizure using Poincaré plot of EEG signals and graphical features in DWT domain. Bratisl Lek Listy. 2023;124(1):12–24. doi: 10.4149/BLL_2023_002. [DOI] [PubMed] [Google Scholar]
- 20.Gutiérrez-Rivas R, et al. Novel real-time low-complexity QRS complex detector based on adaptive thresholding. IEEE Sens J. 2015;15(10):6036–6043. [Google Scholar]
- 21.Arbateni K, Bennia A. Sigmoidal radial basis function ANN for QRS complex detection. Neurocomputing. 2014;145:438–450. [Google Scholar]
- 22.Rahhal Al, Mahmoud M, et al. Deep learning approach for active classification of electrocardiogram signals. Inf Sci. 2016;345:340–354. [Google Scholar]
- 23.Venkatesan C, Karthigaikumar P, Varatharajan RJMT. A novel LMS algorithm for ECG signal preprocessing and KNN classifier Based abnormality detection. Multimedia Tools Appl. 2018;77(8):10365–10374. [Google Scholar]
- 24.Akbari H, et al. Depression detection based on geometrical features extracted from SODP shape of EEG signals and binary PSO. Traitement du Signal. 2021;38(1):13–26. [Google Scholar]
- 25.Hua J, Zhang H, Liu JZ, et al. Direct arrhythmia classification from compressive ECG signals in wearable health monitoring system. J Circ, Syst Comput. 2018;27(6):1–13. [Google Scholar]
- 26.Akbari H, Sadiq MT, Rehman AU. Classification of normal and depressed EEG signals based on centered correntropy of rhythms in empirical wavelet transform domain. Health Inf Sci Syst. 2021;9:1–15. doi: 10.1007/s13755-021-00139-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kiranyaz S, Ince T, Gabbouj M. Real-time patient-specific ECG classification by 1-D convolutional neural networks. IEEE Trans Biomed Eng. 2015;63(3):664–675. doi: 10.1109/TBME.2015.2468589. [DOI] [PubMed] [Google Scholar]
- 28.Sadiq MT, et al. Alcoholic EEG signals recognition based on phase space dynamic and geometrical features. Chaos, Solitons Fractals. 2022;158:112036. [Google Scholar]
- 29.Banerjee S, Girish KS. Agent-based beat-by-beat compression of 12-lead electrocardiogram signal using adaptive Fourier decomposition. Biomed Signal Process Control. 2022;75:103628. [Google Scholar]
- 30.Sadiq MT, et al. Motor imagery BCI classification based on multivariate variational mode decomposition. IEEE Trans Emerg Topics Comput Intel. 2022;6(5):1177–1189. [Google Scholar]
- 31.Pölzl L, et al. Impact of myocardial injury after coronary artery bypass grafting on long-term prognosis. Eur Heart J. 2022;43(25):2407–2417. doi: 10.1093/eurheartj/ehac054. [DOI] [PubMed] [Google Scholar]
- 32.Jahmunah V, et al. Explainable detection of myocardial infarction using deep learning models with Grad-CAM technique on ECG signals. Comput Biol Med. 2022;146:105550. doi: 10.1016/j.compbiomed.2022.105550. [DOI] [PubMed] [Google Scholar]
- 33.Remya RS, Indiradevi KP, Babu KA. Classification of myocardial infarction using multi resolution wavelet analysis of ECG. Procedia Technol. 2016;24:949–956. [Google Scholar]
- 34.Sharma LN, Tripathy RK, Dandapat S. Multiscale energy and eigenspace approach to detection and localization of myocardial infarction. IEEE Trans Biomed Eng. 2015;62(7):1827–1837. doi: 10.1109/TBME.2015.2405134. [DOI] [PubMed] [Google Scholar]
- 35.Sharma LD, Sunkaria RK. Inferior myocardial infarction detection using stationary wavelet transform and machine learning approach. Signal, Image Video Process. 2018;12(2):199–206. [Google Scholar]
- 36.Hannun AY, et al. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nat Med. 2019;25(1):65–69. doi: 10.1038/s41591-018-0268-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Acharya UR, et al. Application of deep convolutional neural network for automated detection of myocardial infarction using ECG signals. Inf Sci. 2017;415:190–198. [Google Scholar]
- 38.Lui HW, King LC. Multiclass classification of myocardial infarction with convolutional and recurrent neural networks for portable ECG devices. Inf Med Unlocked. 2018;13:26–33. [Google Scholar]
- 39.Kumar M, Ram BP, Rajendra Acharya U. Automated diagnosis of myocardial infarction ECG signals using sample entropy in flexible analytic wavelet transform framework. Entropy. 2017;19(9):488. [Google Scholar]
- 40.Han C, Shi Li. ML-ResNet: A novel network to detect and locate myocardial infarction using 12 leads ECG. Comput Methods Programs Biomed. 2020;185:105138. doi: 10.1016/j.cmpb.2019.105138. [DOI] [PubMed] [Google Scholar]
- 41.Li W, et al. SLC-GAN: An automated myocardial infarction detection model based on generative adversarial networks and convolutional neural networks with single-lead electrocardiogram synthesis. Inf Sci. 2022;589:738–750. [Google Scholar]
- 42.Ko W-Y, et al. Detection of hypertrophic cardiomyopathy using a convolutional neural network-enabled electrocardiogram. J Am Coll Cardiol. 2020;75(7):722–733. doi: 10.1016/j.jacc.2019.12.030. [DOI] [PubMed] [Google Scholar]
- 43.Song Y, et al. Deep learning-based automatic segmentation of images in cardiac radiography: A promising challenge. Comput Methods Prog Biomed. 2022;220:106821. doi: 10.1016/j.cmpb.2022.106821. [DOI] [PubMed] [Google Scholar]
- 44.Tigga NP, Shruti G. Efficacy of novel attention-based gated recurrent units transformer for depression detection using electroencephalogram signals. Health Inf Sci Syst. 2023;11(1):1–17. doi: 10.1007/s13755-022-00205-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Tian C, et al. Dual-encoder VAE-GAN with Spatiotemporal Features for Emotional EEG Data Augmentation. IEEE Trans Neural Syst Rehabil Eng. 2023 doi: 10.1109/TNSRE.2023.3266810. [DOI] [PubMed] [Google Scholar]
- 46.Mourad N. ECG denoising based on successive local filtering. Biomed Signal Process Control. 2022;73:103431. [Google Scholar]
- 47.Li Y, et al. A quantum mechanics-based framework for EEG signal feature extraction and classification. IEEE Trans Emerg Topics Comput. 2020;10(1):211–222. [Google Scholar]
- 48.Hao T, et al. Linear and nonlinear analyses of heart rate variability signals under mental load. Biomed Signal Process Control. 2022;77:103758. [Google Scholar]
- 49.Power JR, et al. Electrocardiographic manifestations of immune checkpoint inhibitor myocarditis. Circulation. 2021;144(18):1521–1523. doi: 10.1161/CIRCULATIONAHA.121.055816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zlotoff DA, et al. Electrocardiographic features of immune checkpoint inhibitor associated myocarditis. J Immunother Cancer. 2021;9(3):2007. doi: 10.1136/jitc-2020-002007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Peimankar A, Puthusserypady S. DENS-ECG: a deep learning approach for ECG signal delineation. Expert Syst Appl. 2021;165:113911. [Google Scholar]
- 52.Malia BK, et al. Distributed quantum sensing with mode-entangled spin-squeezed atomic states. Nature. 2022;612:661–665. doi: 10.1038/s41586-022-05363-z. [DOI] [PubMed] [Google Scholar]
- 53.da Silva N, Manuel G, da Joãoaulo VM, Danielo GG. On designing a biosignal-based fetal state assessment system: A systematic mapping study. Comput Methods Prog Biomed. 2022;261:106671. doi: 10.1016/j.cmpb.2022.106671. [DOI] [PubMed] [Google Scholar]
- 54.Song Y, et al. Dynamic hybrid mechanism-based differential evolution algorithm and its application. Expert Syst Appl. 2023;213:118834. [Google Scholar]
- 55.Attallah O. ECG-BiCoNet: An ECG-based pipeline for COVID-19 diagnosis using Bi-Layers of deep features integration. Comput Biol Med. 2022;142:105210. doi: 10.1016/j.compbiomed.2022.105210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Barbosa VADF, et al. Covid-19 rapid test by combining a random forest-based web system and blood tests. J Biomol Struct Dynam. 2021;40(22):11948–11967. doi: 10.1080/07391102.2021.1966509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Sarkaleh MK, Asadollah S. Classification of ECG arrhythmias using discrete wavelet transform and neural networks. Int J Comput Sci Eng Appl. 2012;2(1):1. [Google Scholar]
- 58.Piazza I, et al. Early diagnosis of acute myocarditis in the ED: proposal of a new ECG-based protocol. Diagnostics. 2022;12(2):481. doi: 10.3390/diagnostics12020481. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.