FIGURE 3.

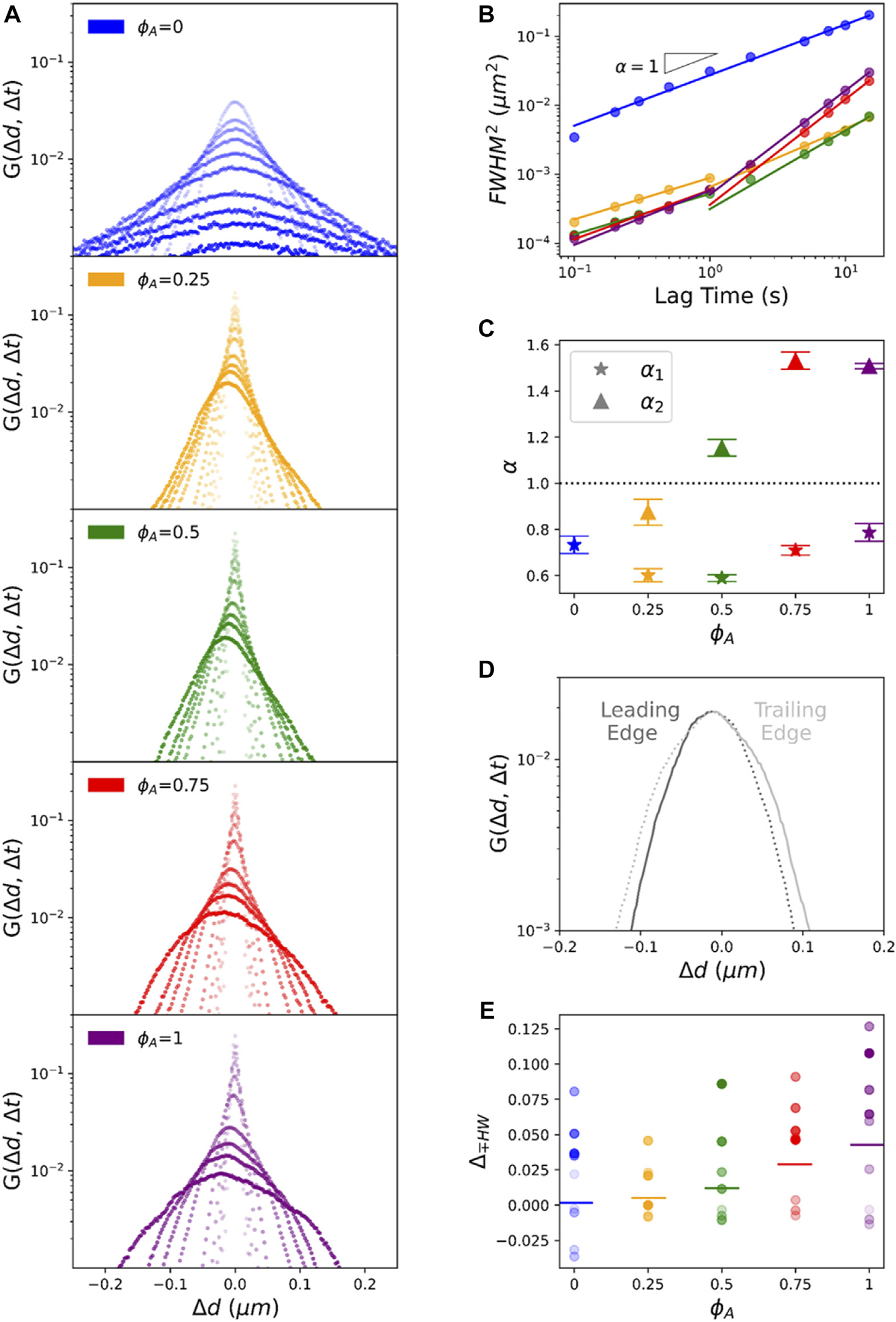
Asymmetric non-Gaussian van Hove distributions reveal a combination of heterogeneous subdiffusion and advective transport of particles in active composites. (A) van Hove distributions $G(\mathrm{\Delta }d,\mathrm{\Delta }t)$ of particle displacements $\mathrm{\Delta }d=\mathrm{\Delta }x\cup \mathrm{\Delta }y$, measured via SPT, for lag times $\mathrm{\Delta }t=0.1,0.2,0.3,0.5,1,2,3,5,10,15s$ denoted by the color gradient going from light to dark for increasing $\mathrm{\Delta }t$. Each panel corresponds to a different composite demarked by their ${\varphi }_A$ value with color-coding as in Figure 2. (B) The square of the full width at half-maximum ${(FWHM)}^2$ versus lag time $\mathrm{\Delta }t$ for each composite shown in (A). Solid lines are fits to $(FWHM{)}^2~\mathrm{\Delta }{t}^{{\alpha }_i}$. For ${\varphi }_A>0$ composites we fit short $(\mathrm{\Delta }t\le 1\mathrm{s})$ and long $(\mathrm{\Delta }t\ge 1\mathrm{s})$ lag time regimes separately. (C) The scaling exponents $\alpha$ as functions of ${\varphi }_A$ determined from the fits shown in B, where ${\alpha }_1$ (stars) and ${\alpha }_2$ (triangles) correspond to scalings for the short and long $\mathrm{\Delta }t$ regimes, respectively. The dashed horizontal line denotes scaling for normal Brownian diffusion. (D) A sample $G(\mathrm{\Delta }d,\mathrm{\Delta }t)$ distribution (${\varphi }_A=0.75$ at $\mathrm{\Delta }t=10\mathrm{s}$) showing the asymmetry about the mode value $\mathrm{\Delta }{d}_{peak}$. We divide each distribution into a leading edge (dark grey, displacements of the same sign as $\mathrm{\Delta }{d}_{peak}$ and greater in magnitude) and the trailing edge (light grey, the remaining part of the distribution). To clearly demonstrate the asymmetry, we mirror each edge about $\mathrm{\Delta }{d}_{peak}$ using dashed lines. (E) The fractional difference of the half-width at half maximum $HWHM$ of the trailing (−) edge from the leading (+) edge, $\left.\left({△}_{\mp HW}=HWH{M}_{-}-HWH{M}_{+}\right)/HWH{M}_{+}\right)$ for each ${\varphi }_A$ and $\mathrm{\Delta }t$. Color coding and gradient indicate ${\varphi }_t$ and $\mathrm{\Delta }t$, respectively, as in (A). Horizontal bars through each distribution denote the mean.