Abstract
Circular-array-based photoacoustic computed tomography (CA-PACT) is a promising imaging tool owing to its broad acoustic detection coverage and fidelity. However, CA-PACT suffers from poor image quality outside the focal zone along both elevational and lateral dimensions. To address this challenge, we proposed a novel reconstruction strategy by integrating the synthetic aperture focusing technique (SAFT) with the 2nd derivative-based back projection (2nd D-BP) algorithm to restore the image quality outside the focal zone along both the elevational and lateral axes. The proposed solution is a two-phase reconstruction scheme. In the first phase, with the assistance of an acoustic lens, we designed a circular array-based SAFT algorithm to restore the resolution and SNR along the elevational axis. The acoustic lens pushes the boundary of the upper limit of the SAFT scheme to achieve enhanced elevational resolution. In the second phase, we proposed a 2nd D-BP scheme to improve the lateral resolution and suppress noises in 3D imaging results. The 2nd D-BP strategy enhances the image quality along the lateral dimension by up-converting the high spatial frequencies of the object’s absorption pattern. We validated the effectiveness of the proposed strategy using both phantoms and in vivo human experiments. The experimental results demonstrated superior image quality (7-fold enhancement in elevational resolution, 3-fold enhancement in lateral resolution, and an 11-dB increase in SNR). This strategy provides a new paradigm in the PACT system as it significantly enhances the spatial resolution and imaging contrast in both the elevational and lateral dimensions while maintaining a large focal zone.
Keywords: Circular array transducer, PACT, Acoustic lens, SAFT, Re-derivative, Back projection
1. Introduction
Photoacoustic (PA) tomography has emerged as a promising medical imaging technology [1], [2], [3], [4]. By converting optical energy into acoustic energy, which is 2–3 orders of magnitude less scattered than photons, PA imaging breaks the optical diffusion limit (1 mm in biological tissue) and significantly extends the imaging depth to ranges that are inaccessible by conventional optical imaging. Generally, PA imaging is classified into two major implementations: scanning-based photoacoustic microscopy (PAM) [5], [6] and reconstruction-based photoacoustic computed tomography (PACT) [7], [8]. Transducer arrays with multiple elements are typically used for PA signal detection in PACT, which significantly enhances the imaging speed compared with a single-element transducer that requires point-by-point scanning in the case of PAM. Linear arrays are widely used for PA imaging owing to the advantageous handheld operation. However, the acceptance angles of linear array transducers are considerably restricted, which results in reconstruction artifacts and deviations [9], [10]. In contrast, curved transducer arrays, especially circular transducer arrays, have a much broader acoustic detection coverage [11], [12], [13]. Circular-array-based PACT (CA-PACT) detects PA waves over a large field of view, which helps reduce the partial-view detection issue in the imaging plane and offers images with enhanced imaging fidelity. The 3D tomography of CA-PACT is achieved based on slice stacking, i.e., mechanical scanning is employed along the elevational axis. Owing to the geometrical shape of acoustic detection, CA-PACT is well suited for the visualization of cylindrical and oblong targets, such as the entire body of small animals [14], [15] and the peripheral blood vessels of human arms and legs [8]. Therefore, CA-PACT exhibits significant potential in peripheral vasculature-related clinical research. However, the imaging quality of CA-PACT is generally limited by the elevational resolution. To realize a high elevational resolution, a focused ultrasound transducer (UST) array with a large elevation NA and high center frequency is usually employed. Unfortunately, CA-PACT only produces a high-resolution image in the focal zone but fails to maintain its performance within the out-of-focus region [16], [17], thereby deteriorating its sectioning capability. Moreover, owing to the finite detector aperture size, the limited view angle and the transducer frequency, the inadequate image quality along the lateral (transverse) dimension also restricts the tomography of CA-PACT. The lateral resolution indicates the minimum resolvable distance between two point targets, parallel to the detector array. The degraded image quality along both the elevational and lateral dimensions significantly hinders the high-resolution 3D imaging of CA-PACT.
To compensate for this incapability, some solutions have been proposed. One strategy is to deconvolve the raw data based on the acoustic point spread function (PSF) to retrieve the broadband PA signals [18], [19]. This helps improve the spatial resolution in both the elevational and cross-sectional plane directions. However, obtaining a pixel-varying PSF map in a 3D manner is very challenging, given that the PSF is not only spatially-varying in the cross-sectional plane but also focal depth-dependent in the elevational axis. Another alternative is the use of the deep learning method [20], [21], wherein high-resolution images within the focal zone are used as the ground truth to enhance the out-of-focus images via neural network training. However, a considerably large dataset, including acquired images and their corresponding ground truth, is required for training, validation, and testing, leading to heavy computational burdens. As opposed to deep learning approaches which require the use of bulky datasets, the SAFT-based scheme needs only the raw PA data for image formation, thereby reducing the data-acquisition and computational burdens. SAFT is an image reconstruction technique that has been applied in acoustic-resolution PAM [22], [23], [24], [25], [26], [27], [28], [29] and photoacoustic endoscopic (PAE) imaging [30], [31]. With the application of the virtual detector (VD) concept [22], [23], SAFT can enhance the out-of-focus lateral resolution of PAM and PAE systems. More recently, SAFT has been introduced to PACT imaging [32], [33] to improve the elevational resolution. However, the efficacy of the SAFT approach is limited by the in-focus resolution of the PACT system. Furthermore, the SAFT-based approach can only enhance the image resolution along the elevational axis whereas has little effect on the lateral dimension, and the processed results remain blurred and deteriorated along the lateral axis. Moreover, the demonstration of in vivo imaging, particularly the 3D in vivo demonstration, is still rare in the state-of-the-art [32], [33], [34].
To address these challenges, we have developed a novel technique by integrating SAFT with the 2nd derivative back projection scheme in this study. Unlike the conventional SAFT scheme, our proposed method restores the image quality in both the elevational and lateral dimensions. The solution is a two-phase restoration method. In the first phase, we designed a circular-array-based SAFT algorithm to address the deteriorated elevational resolution in the out-of-focus region. By employing an acoustic lens, the position of the virtual point of the SAFT was varied, and the elevational resolution outside the focal region was improved beyond the upper limit defined by the conventional SAFT approach. In the second phase, we propose a 2nd derivative back projection (2nd D-BP) scheme to enhance the lateral resolution by reinforcing the frequency components resulting from the CA-SAFT reconstruction. The lateral resolution was improved by up-converting the high spatial frequencies of the absorption pattern of the object. The synthesis between these two phases manifests unique merits because the SAFT-based approach in the first phase reduces the highly anisotropic frequency components in the original image and helps prevent the elimination of the originally low-frequency contents in the second phase. The combination of these two phases facilitated the restoration of the image quality of CA-PACT. The efficacy of the proposed approach was evaluated through both phantoms and in vivo human experiments. We quantitatively compared the CA-SAFT scheme and our CA-SAFT+ 2nd D-BP and demonstrated the superiority of our technique. The proposed strategy provides new opportunities for the PACT system to simultaneously achieve high resolution and high imaging contrast in both the elevational and lateral dimensions while maintaining a large focal zone.
2. Method and materials
2.1. CA-PACT system
Fig. 1a shows a schematic of our custom-built CA-PACT imaging system, which comprises a nanosecond pulsed laser, customized fiber bundle, circular transducer array (semi-ring shape), acoustic lens, data acquisition (DAQ) module, and translation stage. Briefly, an optical parametric oscillator laser (Innolas GmbH, Bonn, Germany; 4–6-ns pulse duration) was used to deliver laser pulses at a repetition rate of 20 Hz with a wavelength tunable from 680 to 980 nm. The laser pulse was attenuated by a combination of a half-wave plate and a Glan prism before being coupled into a customized 1 × 10 fiber bundle (Nanjing Chunhui Corp., China) via a fiber coupler. The branches of the fiber bundles were evenly distributed along the arc of the semi-circular transducer array (Fig. 1a). The laser light from the end of each branch illuminated the imaging object and excited the PA signals. The PA signals were detected by a customized circular transducer array (Doppler Electronic Technologies Corp, China; 256 elements) with a 5-MHz central frequency (∼70% bandwidth). The 256 elements (10-mm height) of the transducer array were spaced with a pitch of 0.858 mm. Each element is cylindrically focused with an elevational focal distance of 70 mm (NA, 0.07), thereby producing an elevational resolution of 3 mm in focus for slice imaging along the elevational direction. An acoustic lens, indicated by the blue component in Fig. 1a, was employed to modify the elevational NA. The acoustic lens, made of polystyrene (1.05 g/cm3 mass density), was purchased from Doppler Electronic Technologies Co.,Ltd (Guangzhou, China) and has an elevational dimension of 10 mm × 40 mm (elevational height × focal distance). To be more specific, the acoustic lens effectively shifts the focal point from the center of the semicircle of the ultrasound transducer (UST) to a new position that is 40 mm away from the transducer array surface (Fig. 1b). This configuration helps achieve a higher NA (0.125) relative to the original system (NA 0.07). This arrangement helps improve the in-focus resolution beyond that defined by the original PACT system. With a pulse energy of 30 mJ and a striped illumination area of 10 cm2 on the imaging object, the optical fluence on the surface of the target was approximated to be 3 mJ/cm2, which was well below the ANSI safety limit (34 mJ/cm2 at 820-nm wavelength and 20-Hz pulse repetition rate).
Fig. 1.
(a) Schematic of the CA-PACT imaging system. λ/2: half-wave plate. DAQ: data acquisition module. (b) Graphical illustration of the focusing-related PA signal distortions (blue dashed lines) that occur in the CA-PACT system, viewed from the front elevation. Red dot: the imaging target. PAi (PA1, PA2, and PA3) indicate the detected PA signal of a point target when the UST scans at position Pi (i = 1, 2, 3) for the case of the target being situated on the left side of the focal plane. Conversely, for the case of the target being positioned on the right side of the focal plane, PAi' (PA1', PA2', and PA3') were used to represent the detected PA signals during the scanning of the UST. W: elevational height (10 mm) of both the UST and the acoustic lens.
To achieve slice-stacking 3D imaging, a motorized translation stage controlled by the LabVIEW system (2011, National Instruments, TX, USA) was employed to drive the transducer array to mechanically scan along the elevational axis. During the elevational scanning, the center of the imaging plane exhibits the sectioning ability owing to the elevational focus shaped by the UST array. However, imaging objects outside the focal zone suffer from defocusing distortions and artifacts. As portrayed in Fig. 1b, the PA signals of the targets (red dots) display a concavely/convexly distorted shape (dashed blue line) owing to the difference in the time-of-flight required for a target’s signal to reach a curved transducer element. Detailed elaborations on the mechanism and essence of the concave/convex focusing-related distortions are geometrically illustrated in Ref. [29]. The inherent artifacts and distortions of the CA-PACT system outside the elevational focus inevitably degrade the image quality.
2.2. SAFT-based algorithm
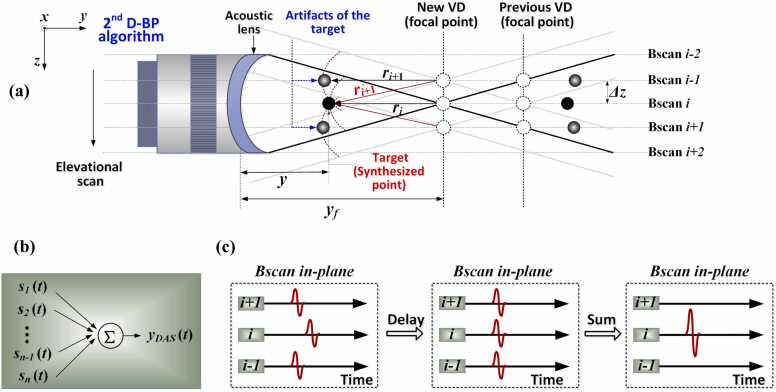
The VD-based SAFT-based reconstruction strategy was used to eliminate the out-of-focus distortions and artifacts in CA-PACT and restore the elevational imaging quality out-of-focus. Fig. 2a outlines the essential principle of the VD-based SAFT scheme, wherein the elevational focal point of the UST element is considered as the VD for the detection of the PA signals. With the employment of the acoustic lens, the position of the VD is altered from the center of the semicircle to the position of the new focus, as shown in Fig. 2a. The mechanical scanning is conducted along the z-axis, and each dashed-line perpendicular to the elevational direction signifies a cross-sectional image (i.e., Bscan image) in the x–y plane. In Fig. 2a, the black dots indicate the imaging targets, which are also considered as the synthesized points in the algorithm. The gray dots signify the artifacts of the target when the CA-transducer moves from Bscan (i) to Bscan (i-1) or Bscan (i + 1), which are generated owing to the repeated detection of the targets at the corresponding Bscan. To recover the elevational imaging quality at any arbitrary scanning position i, the correlated signals detected at adjacent Bscans are synthesized with compensation for their acoustic propagation delays [22], [23].
| (1) |
where indicates the original raw PA data recorded at scanning position i, denotes the PA signal processed with SAFT, defines the adjacent Bscans involved in the summation, the total number (N) of which depends on the PA detection range and is elaborated below. Eq. 1 indicates the delay and sum (DAS) beamforming procedure (Fig. 2b) performed on a pixel-by-pixel basis. In the DAS process, an appropriate time delay () is applied to the detected signal in the vicinity of the ith Bscan (Fig. 2c). The correlated signals are adjusted such that they are in the same phase (Fig. 2c, middle) to be properly synthesized (Fig. 2c, right).
Fig. 2.
Schematic of the VD-based SAFT strategy for CA-PACT systems. (a) Geometric demonstration of the SAFT model, viewed from the front elevation. and: the length of the synthesized point (target) and VD, respectively, estimated from the surface of the UST. and : the distance between the synthesized point (target) and VD at scanning position i and i+1, respectively. : the distance between the detected artifact of the target and focal point when the UST moves to position i+1. : elevational scanning step of the UST. (b) Concept of the DAS algorithm. (c) Synthesis of correlated signals using DAS. Left: originally detected signal in the vicinity of the ith Bscan; Middle: time-delayed version of signals, adjusted to be in the same vertical plane (i.e., in phase); Right: newly generated signal in the ith Bscan after summation.
The time delay () is estimated according to the difference in the detection time. For Bscan (i+1) shown in Fig. 2a, the time delay () relative to Bscan (i) is calculated as , and is further quantified as. This is because of the geometrical relationship , as can be seen from Fig. 2a. As a more generic description, the time delay at an arbitrary Bscan (i+j) relative to Bscan (i) can be expressed as
| (2) |
where signifies the straight distance between the synthesized point and VD at the scanning position and is quantified as , wherein denotes the elevational scanning step of the UST between adjacent Bscans. In Eq. 2, sign is the signum function, and and indicate the distances of the synthesized point (target) and VD, respectively, estimated from the center of the UST detection surface. The implementation of (1), (2) enables a set of new Bscans to be synthetically generated along the elevational axis. To further enhance the focusing quality, coherent factor (CF) weighting is applied to suppress noises and artifacts [22], [23], [35], [36].
| (3) |
is an effective measure of the phase relation of adjacent signals [37], [38], [39], the value of which ranges from 0 to 1 and is applied to the output of the DAS-based SAFT.
| (4) |
Eq. 4 indicates a preservation of the main-lobe signals and suppression of the side-lobes/background noise. For the main lobes, the summation of the delayed signals is constructive. This leads to a high CF value (close to 1); thus, the outputs of SAFT are maintained (Eq. 4). In contrast, the CF values are minimized (close to 0) for the side lobes and background noises because of the destructive summation in such cases. The minimized CF value gives rise to the suppression of the SAFT output of artifacts and noises (Eq. 4).
To determine the number of neighboring Bscans (N) involved in the SAFT, we use the spatial impulse response (SIR) of the transducer to account for the change in N with the focal distance. Therefore, a binary weighting mask () is applied to multiply the output of the SAFT.
| (5) |
where the notation indicates a binary contribution map of the SIR, which equals 1 when pixel () is within the SIR region and 0 otherwise. For simplification, a linear function () is used as the binary weighting mask for the SIR, where w indicates the transducer width. This implies that the SIR mask specifies that the pixels involved in the signal summation are encompassed by the crossed area of the two solid black lines in Fig. 2a. After considering the SIR weighting, the CF is modified as follows:
| (6) |
(5), (6) indicate that SAFT and CF are performed for pixels located only within the SIR region, after which the final output signal () should be rectified. This SIR-weighted CF-based SAFT algorithm designed for the CA-PACT system is referred to as the CA-SAFT solution for simplicity, and the incorporation of the CA-SAFT algorithm with the acoustic lens is referred to as the CA-SAFT-Lens strategy in this study. A flowchart of this strategy is presented in Fig. 3 (first row).
Fig. 3.
Schematic and flow chart of the proposed CA-SAFT+ 2nd D-BP strategy.
2.3. 2nd derivative-based BP algorithm
The outputs of the CA-SAFT solution were then used as the inputs of the universal back-projection (BP) algorithm [40] for the image formation in the x–y plane, as delineated in Fig. 2a (top left, x-y dimension), such that the circular geometry cross-sectional images are acquired. Subsequently, the reconstructed Bscans are combined next to each other along the elevational axis to form a 3D slice-stacking tomographic image. In the conventional BP algorithm, the back-projection term related to the measurement is given as
| (7) |
where denotes the detected acoustic pressures at positions and time . In our 2nd derivative BP strategy, as illustrated in Fig. 3 (second row), we applied the re-derivative-based BP approach to reinforce the high-frequency components and suppress noise and distorted signals. More specifically, the back-projection term is used to replace the role of the original raw data (i.e., ) in Eq. 7, implying that the calculation procedure of Eq. 7 is repeated.
| (8) |
The term is considered as the new back-projection term and is used for the subsequent calculation of DAS to reconstruct the image in the x-y plane. This procedure up-converts the high spatial frequencies of the absorption pattern of an object in the frequency domain. In Eq. 8, the component plays a dominating role in the back projection term, thus this strategy is termed as the 2nd derivative back projection and is denoted as 2nd D-BP throughout this paper. Unlike CA-SAFT, which enhances the elevational resolution, the 2nd D-BP solution alters the image quality in the lateral direction. This is because the former (CA-SAFT) synthesizes the signal lengthwise along the elevational axis, whereas the latter (2nd D-BP) reconstructs signals in the x-y plane, and the 3D tomographic images were obtained based on slice-stacking of the cross-sectional images (i.e., Bscan). As such, the effect of the 2nd D-BP scheme is considered independent of the elevational axis. A flowchart of the proposed two-phase strategy (CA-SAFT and 2nd D-BP) for enhancing both the elevational and lateral resolutions is shown in Fig. 3 (third row).
2.4. Post-processing
MATLAB 2017b was used for the data processing and image reconstruction. The reconstructed 3D PA volume demonstrated in this study was produced using 3DPHOVIS, a photoacoustic visualization software package developed by Kim et al. [41]. In addition, a skin profile estimator provided by 3DPHOVIS [41] was used in this study to remove the superficial skin for the in vivo imaging results (Section 3.2.2), such that the vessels underneath the skin were revealed.
3. Results
We first evaluated the effectiveness of the designed strategy, i.e., the integration of the SAFT algorithm with the acoustic lens, the outcomes of which are presented in Section 3.1. After demonstrating the advantages of the CA-SAFT-Lens scheme, we investigated the feasibility and efficacy of the proposed CA-SAFT+ 2nd D-BP. The results are demonstrated in detail in Section 3.2.
3.1. CA-SAFT scheme with and without acoustic lens
3.1.1. Human rib model
To evaluate the image quality enhancement realized using the CA-SAFT method in a 3D manner, we imaged a human rib model using the CA-PACT system. The human rib model (Fig. 4a), purchased from Zhenghe Teaching Model Co., LTD (Guangzhou, China), was spray-painted before PA imaging to yield sufficiently strong PA signals. Fig. 4 presents representative 3D images of the human rib model before (left column) and after (right column) the application of the SAFT-based reconstruction. The first and second rows in Fig. 4 indicate the PA imaging results obtained with and without the acoustic lens. For the first case, where the acoustic lens was not applied (Fig. 4, first row), we observe a dissatisfying performance of CA-SAFT in improving the elevational resolution, the reason for which stems from the limited difference in spatial resolution between the inside and outside of the focal zone. The separate adjacent rips of the human rib (indicated by the yellow dashed line in Fig. 4c) are nearly indistinguishable using the CA-SAFT approach. For the case of using the acoustic lens (Fig. 4, second row), the image quality improvement in the CA-SAFT images (Fig. 4e) relative to the original image (Fig. 4d) is clearly noticeable. The internal structure of multiple adjacent rips was blurred and unclear in the original image but was evidently resolved in the CA-SAFT results (Fig. 4e).
Fig. 4.
Experimental results of the human rip model. (a) Photograph of the human rip model, wherein the dashed box indicates the PA imaging area. (b-e) The 3D PA imaging results of the human rip model, including (b) original image (no lens), (c) CA-SAFT image (no lens), (d) original image (lens), and (e) CA-SAFT image (lens), respectively.
The comparison between Figs. 4c and 4e verifies the efficacy of the CA-SAFT-lens strategy in pushing the boundary of the achievable resolution outside the focus. More specifically, the conventional SAFT method hardly possesses sectioning ability outside the focal zone in this scenario. By contrast, the proposed CA-SAFT-Lens scheme overcomes this barrier and regains the sectioning capacity of the CA-PACT system. We quantitatively compared the resolution and SNR enhancement of the proposed CA-SAFT method against those of the conventional method by analyzing the line profiles indicated by L1 and L2 shown in Fig. 4b. The measured the full width at half maximum (FWHM) and signal-to-noise ratio (SNR) of each line profile obtained using different approaches are summarized in Table 1. Compared to the no-lens CA-SAFT approach, the CA-SAFT-lens strategy achieves 2-fold enhancement in elevational resolution and a more than 13 dB increase in SNR outside the focal zone, manifesting a considerably enhanced performance of 3D slice-stacking tomographic imaging along the elevational axis.
Table 1.
Measured FWHM and SNR of each line profile.
| Line #1 |
Line #2 |
||||
|---|---|---|---|---|---|
| FWHM | SNR | FWHM | SNR | ||
| No Lens | Original | 5.04 mm | 24.70 dB | 4.20 mm | 12.39 dB |
| CA-SAFT | 4.01 mm | 37.27 dB | 3.40 mm | 29.81 dB | |
| Lens | Original | 8.12 mm | 14.34 dB | NA | 20.48 dB |
| CA-SAFT | 1.96 mm | 50.28 dB | 1.68 mm | 46.17 dB | |
3.1.2. Iron wire phantom
To assess the efficacy of the CA-SAFT-Lens scheme in a sample with a more complex structure, we imaged a phantom consisting of 0.5 mm iron wires with different orientations and depths to mimic the complex distribution of vascular networks (Fig. 5a). The iron wire phantom was placed in the out-of-focus region. Fig. 5 presents the reconstructed 3D images of the phantom structure acquired with and without the CA-SAFT strategy, shown in the left and right columns, respectively. The PA results obtained before and after the application of the acoustic lens are demonstrated in the first and second rows, respectively. Compared to the no-acoustic lens scenario (first row), the images obtained using the acoustic lens (second row) exhibited two features. (i) In the original approach, the images acquired using the lens exhibited worse image quality (Fig. 5d) relative to the no-lens case (Fig. 5b), because the acoustic lens with a large NA led to a rapid decay of image quality within the out-of-focus region. (ii) In the CA-SAFT approach, the reconstructed images obtained using the lens (Fig. 5e) produced much finer image quality (i.e., finer feature size and higher image contrast), as opposed to the no-lens scenario (Fig. 5c). In the first case (lens applied), the resolvability of adjacent filaments was clearly visible as indicated by the yellow dashed line in the MAP image (Fig. 5e). In the second case (no lens), the phantom structures remain unclear and blurred (Fig. 5c). Table 2 lists the measured FWHM and SNR of the line profiles (L1 and L2 shown in Fig. 5b) along the z-axis obtained using different approaches. The elevational resolution achieved by the CA-SAFT solution (Fig. 5c) is better than the original image (Fig. 5b) by 1.75 folds (line #1). On this basis, with the assistance of the acoustic lens, the CA-SAFT-Lens scheme (Fig. 5e) further achieves a 3.8-folds enhancement in the elevational resolution and an 8.2 dB increase in the SNR (line #2) relative to the conventional SAFT scheme. Compared to the original approach (lens applied) shown in Fig. 5d, the CA-SAFT-Lens strategy (Fig. 5e) exhibited a seven-fold increase in the elevational resolution and 29 dB increase in SNR (line #1). These enhancements validate the ability of the designed CA-SAFT-Lens strategy to reveal a complex structure with much finer elevational resolution and imaging contrast.
Fig. 5.
Experimental results of the iron wire phantom. (a) Photograph of the iron wire phantom. (b–e) Corresponding PA imaging results (MAP) of the iron wire phantom, including (b) original image (no lens), (c) CA-SAFT image (no lens), (d) original image (lens), and (e) CA-SAFT image (lens), respectively. L1: Line#1; L2: Line#2.
Table 2.
Measured FWHM and SNR of each line profile.
| Line #1 |
Line #2 |
||||
|---|---|---|---|---|---|
| FWHM | SNR | FWHM | SNR | ||
| No Lens | Original | 7.84 mm | 11.18 dB | NA | 11.20 dB |
| CA-SAFT | 4.48 mm | 31.16 dB | 7.84 mm | 30.77 dB | |
| Lens | Original | 14.84 mm | 8.59 dB | NA | 10.43 dB |
| CA-SAFT | 2.02 mm | 38.03 dB | 2.08 mm | 38.95 dB | |
3.2. CA-SAFT+ 2nd D-BP algorithm
We evaluated the efficacy of the CA-SAFT+ 2nd D-BP scheme through both phantom and in vivo human imaging. All experiments presented in this section were conducted using the CA-PACT system with the acoustic lens.
3.2.1. Iron wire phantom
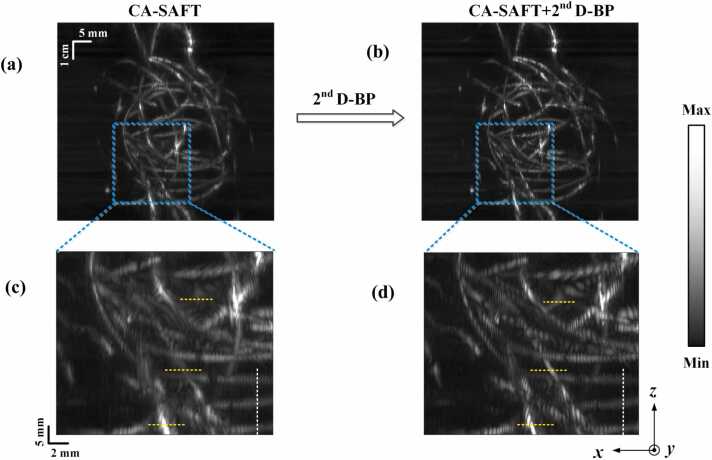
On the basis of CA-SAFT approach, we further employed the 2nd D-BP approach to improve the image quality in the lateral dimension by weighing the high-frequency contents. The CA-SAFT-reconstructed results of the iron wire phantom (Fig. 5e) demonstrated in Section 3.1.2, were used as the input of the 2nd D-BP algorithm to evaluate its efficacy. The CA-SAFT-reconstructed MAP images of the iron wire phantom before and after the application of the 2nd D-BP strategy are presented in Fig. 6a and b, respectively, and close-up visualizations of the phantom details enclosed by blue dashed boxes are demonstrated in Fig. 6c and d. The images obtained using the CA-SAFT+ 2nd D-BP method enabled a clearer identification of the wire pattern. Specifically, the wire structures indicated by the three yellow dashed lines (Fig. 6d) are better resolved using the 2nd D-BP approach, whereas they remain unclear and blurred in the CA-SAFT images (Fig. 6c). A comparison of Fig. 6c and d verifies the improved resolution in the lateral dimension (x-axis). Conversely, the image quality along the elevational dimensions between the two approaches remained practically unchanged, as indicated by the white dashed line along the z-axis. These results are consistent with the analysis of the effects of the CA-SAFT and 2nd D-BP strategies on the image quality presented in Section 2.3. A more detailed and quantitative analysis of the CA-SAFT+ 2nd D-BP approach is presented in the following section.
Fig. 6.
CA-SAFT-reconstructed results of the iron wire phantom before (a) and after (b) the application of the 2nd D-BP method. The close-up visualization of phantom structures enclosed by the blue boxes are demonstrated in (c) and (d), respectively.
3.2.2. In vivo imaging
For in vivo demonstration, we collected the PA data of human hands and foot from a healthy Asian female volunteer to validate the performance of our proposed CA-SAFT+ 2nd D-BP method. Human imaging experiments were conducted according to a protocol approved by the Institutional Review Board (IRB) of Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences (SIAT-IRB-230515-H0654).
3.2.2.1. Human foot
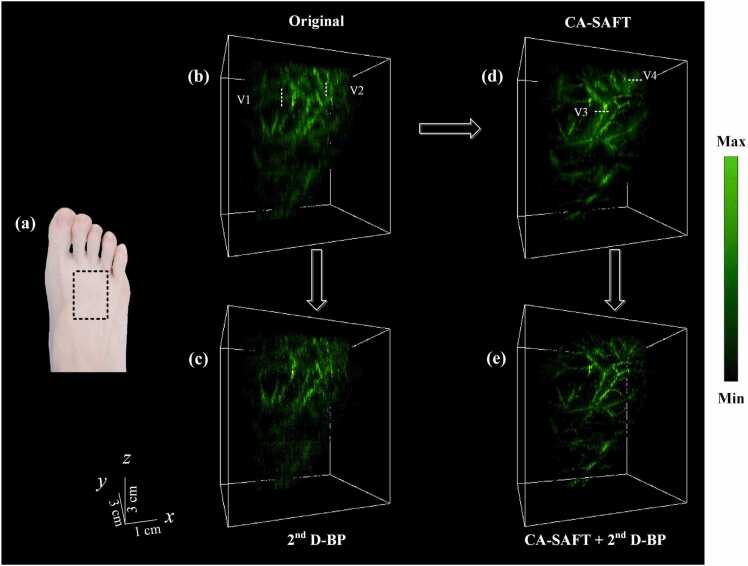
The human foot was placed out of focus, with a region of interest indicated by a white dashed rectangle (Fig. 7a). Fig. 7(b–e) present the reconstructed 3D images of the human foot acquired using the conventional method, 2nd D-BP, CA-SAFT, and CA-SAFT+ 2nd D-BP scheme, respectively. The MAP images along the anterior (XZ) direction of the human foot obtained using the aforementioned approaches are shown in Fig. 8. The blurry image obtained from the conventional methods can be seen in Figs. 7(b) and 8(b), where the blood vessels indicated by the dashed lines V1 and V2 are hardly identified owing to the poor elevational resolution. In contrast, the reconstructed image obtained using the CA-SAFT algorithm (Figs. 7d and 8c) restored the shape of the blood vessels (V1–V2), showing more than a 3-fold improvement in elevational resolution (Table 3). CA-SAFT evidently improved the resolution for elevational vessels (V1-V2), whereas the vessels with vertical components remained blurred (V3–V4), as illustrated in Figs. 7d and 8c. To compensate for this incapability, the 2nd D-BP approach was applied. As shown in Figs. 7e and 8d, the images resulting from the CA-SAFT+ 2nd D-BP scheme enabled a clearer identification of the vessel pattern because of the improved lateral resolution. The scheme of CA-SAFT+ 2nd D-BP also helps suppress noise and distorted signals, thereby enhancing the imaging contrast. The quantitative analyses of the improved resolution and SNR are summarized in Table 3, where the CA-SAFT+ 2nd D-BP method achieves a 2–3 fold increase in lateral resolution and ∼5 dB enhancement of SNR (V4) compared with the CA-SAFT strategy. Relative to the original approach, the strategy of CA-SAFT+ 2nd D-BP exhibited more than 13 dB increase in SNR. CA-SAFT+ 2nd D-BP permits a recovered image quality in both elevational and lateral directions.
Fig. 7.
Experimental results of a human foot. (a) Photograph of the volunteer's right foot, wherein the dashed box indicates the PA imaging area. (b–e) 3D PA imaging results of the human foot using (b) the conventional approach, (c) the 2nd BP method, (d) the CA-SAFT method, and (e) the CA-SAFT-2nd BP method, respectively.
Fig. 8.
MAP images of human foot acquired using (a) the 2nd BP method, (b) the conventional approach, (c) the CA-SAFT method, and (d) the CA-SAFT-2nd BP method, respectively.
Table 3.
Measured FWHM and SNR of each line profile.
| Elevational dimension | Lateral dimension | ||||||||
| V1 | V2 | V3 | V4 | ||||||
| FWHM | SNR | FWHM | SNR | FWHM | SNR | FWHM | SNR | ||
| Original | 6.63 mm | 15.23 dB | NA | 10.81 dB | CA-SAFT | 2.01 mm | 25.46 dB | 3.47 mm | 22.28 dB |
| CA-SAFT | 2.07 mm | 21.54 dB | 2.25 mm | 22.58 dB |
CA-SAFT + 2ndD-BP |
1.06 mm | 29.06 dB | 1.07 mm | 27.48 dB |
To better demonstrate the unique merits of the synthesis of CA-SAFT and 2nd D-BP, the original image processed with only the 2nd D-BP scheme is shown in Figs. 7c and 8a. Compared with Fig. 8b, Fig. 8a exhibits a lower spatial resolution and image contrast particularly along the z-axis. This is exemplified by the vessels labeled by the white dashed lines V5 and V6 in Fig. 8a, the signal of which diminishes in the 2nd D-BP image. This is presumably because the frequency components in the original image are highly anisotropic owing to the low elevational resolution content, and the extraction/amplification of the high-frequency component applied to the entirety of the original data suppresses low-frequency signals, particularly perpendicular to the elevational axis. In contrast, CA-SAFT helps to reduce the anisotropy resolution feature, i.e. helps to homogenize the frequency component by improving the degraded elevational resolution (Figs. 7d and 8c). After this procedure, the 2nd D-BP scheme begins to show efficacy and achieves a much finer image quality for complex structures (Figs. 7e and 8d) by up-converting the frequency components of the object’s absorption pattern.
3.2.2.2. Human hand
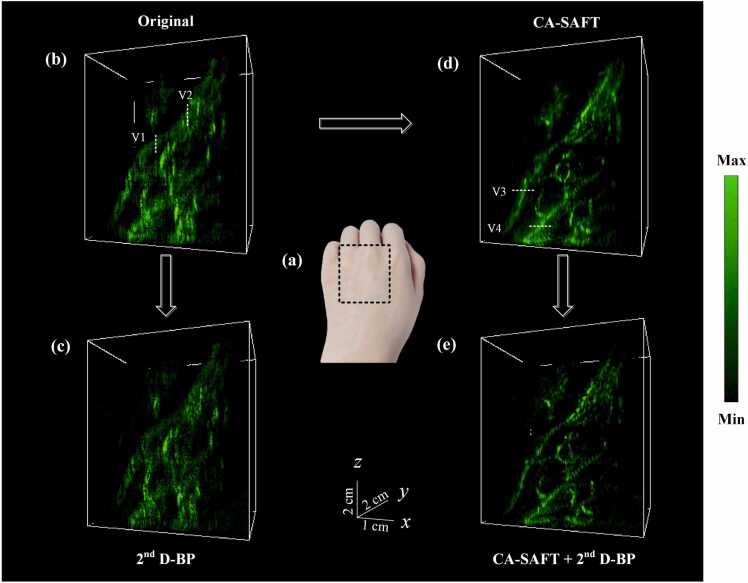
Fig. 9, Fig. 10 demonstrate the 3D imaging results of a human left and right hand, acquired using the aforementioned four approaches. The corresponding MAP images of the left hand are illustrated in Fig. 11. As expected, the degraded elevational resolution shown in the original image were improved using the CA-SAFT approach, as indicated by the vessels labeled by V1–V2 in Fig. 9, Fig. 10. As an extension to CA-SAFT, the 2nd D-BP approach further enhances the imaging quality along the lateral axis by amplifying the high frequency components reinforced by the CA-SAFT. Much finer details of the vasculature are revealed in the CA-SAFT+ 2nd D-BP image, as depicted in Figs. 9e and 10e. The vessels indicated by white dashed line V3-V4 in Figs. 10d and 11c, manifest 2–4 folds improvement of lateral resolution and 5 dB increase of SNR in the CA-SAFT+ 2nd D-BP image relative to the CA-SAFT image, as summarized in Table 4. Compared to the original approach, the strategy of CA-SAFT+ 2nd D-BP exhibits more than 11 dB enhancement of SNR. These results again testified to the superior performance of the proposed CA-SAFT+ 2nd D-BP solution in restoring the degraded image quality in both the elevational and lateral dimensions. Consequently, the enhanced visualization of peripheral vascular networks can be achieved.
Fig. 9.
Experimental results of a human right hand. (a) Photograph of the volunteer's right hand, wherein the dashed box indicates the PA imaging area. (b–e) 3D PA imaging results of the human right hand using (b) the conventional approach, (c) the 2nd BP method, (d) the CA-SAFT method, and (e) the CA-SAFT-2nd BP method, respectively.
Fig. 10.
Experimental results of a human left hand. (a) Photograph of the volunteer's left hand, wherein the dashed box indicates the PA imaging area. (b–e) 3D PA imaging results of the human left hand using (b) the conventional approach, (c) the 2nd BP method, (d) the CA-SAFT method, and (e) the CA-SAFT-2nd BP method, respectively.
Fig. 11.
MAP images of the human left hand acquired using (a) the 2nd BP method, (b) the conventional approach, (c) the CA-SAFT method, and (d) the CA-SAFT-2nd BP method, respectively.
Table 4.
Measured FWHM and SNR of each line profile.
| Elevational dimension | Lateral dimension | ||||||||
| V1 | V2 | V3 | V4 | ||||||
| FWHM | SNR | FWHM | SNR | FWHM | SNR | FWHM | SNR | ||
| Original | 7.84 mm | 16.83 dB | 7.28 mm | 22.95 dB | CA-SAFT | 1.80 mm | 20.86 dB | 1.91 mm | 23.44 dB |
| CA-SAFT | 2.83 mm | 24.41 dB | 2.53 mm | 32.05 dB |
CA-SAFT + 2ndD-BP |
0.99 mm | 25.02 dB | 0.53 mm | 28.89 dB |
4. Discussion and conclusions
CA-PACT is an important imaging modality in PA imaging but suffers from poor image quality outside the focal zone along the elevational and lateral dimensions. Typically, a focused transducer array with a large NA is applied in CA-PACT to achieve a high elevational resolution, but the image quality rapidly decays within the out-of-focus region, wherein the spatial resolution and SNR exhibit a major deterioration. Moreover, the inadequate image quality along the lateral dimension also restricts the 3D tomography of CA-PACT. To overcome this limitation, we proposed a novel reconstruction method that integrates the SAFT scheme with the 2nd D-BP to restore the image quality outside the focal zone in both the elevational and lateral dimensions. Compared with previous studies, our strategy exhibits the following advantages. (i) The SAFT approach eliminates the dependence of image quality on the in-plane imaging radius and enlarges the focal zone substantially. In other words, this approach overcomes the trade-off between the elevational resolution and the focal zone of the CA-PACT system. (ii) The incorporation of an acoustic lens with the CA-SAFT algorithm surpasses the upper limit of the conventional SAFT scheme to achieve a high elevational resolution outside the focal region, and helps regain the sectioning ability of the CA-PACT system outside the focal zone. The adjacent structures in the elevational axis are nearly indistinguishable when using the conventional SAFT method (Figs. 4c and 5c) but are clearly resolvable in the CA-SAFT-Lens approach (Figs. 4e and 5e). (iii) By integrating the 2nd D-BP scheme with the SAFT approach, the lateral resolution was enhanced via the reinforcement of the high-frequency components of the absorption pattern of the object in the frequency domain. The effectiveness of this strategy was validated by both phantom and in vivo human imaging, the results of which exhibited more than 7-fold enhancement in the elevational resolution (Figs. 5), 3-fold enhancement in the lateral resolution (Figs. 7 and 10), and more than 11-dB increase in SNR (Fig. 7, Fig. 10). The 3D visualization of the human hands and foot demonstrates the ability of the algorithm to image complex in vivo structures with high resolution and high imaging contrast in both the elevational and lateral dimensions while maintaining a large focal zone.
When applying the designed CA-SAFT-Lens strategy, the following consideration needs to be taken into account.
-
(i)
The VD-based CA-SAFT approach is very sensitive to motion artifacts because CA-SAFT assumes that the time delays of PA signals between adjacent Bscans are caused only by the curved UST during scanning and not by the physiologically relevant motion artifacts. In the current study, the human hands and foot were used for in vivo studies to minimize the motion artifacts. However, motion-correction strategies maybe required to compensate for physiologically relevant motion artifacts when imaging animals with negligible motion artifacts, such as mice with significant heart-beating-induced and respiration-induced motion artifacts. In the future, time-gated strategies and image registration algorithms are expected to be incorporated into CA-SAFT to tackle this problem. For instance, by capturing animal’s respiratory waveform and reconstruct image at the same respiratory phase, we may minimize motion artifacts induced by respiratory-based rhythmic movements. Similarly, cardiac gating methods can be employed to synchronize data acquisition with specific phases of the cardiac cycle, mitigating motion artifacts caused by heartbeats. Furthermore, image registration algorithms, including intensity-based and feature-based automatic registration schemes, are expected to be employed to ensure accurate alignment and positioning of imaging objects. These algorithms enable the fusion of multiple frames or volumes acquired at different time points, facilitating improved spatial correspondence and alignment.
-
(ii)
The optical illumination area should exceed the acoustic detection region (i.e., the SIR region) for the SAFT-based algorithm to take effect. This prerequisite guarantees that the research topic belongs to an acoustic inversion issue such that the SAFT-based approach can be used to address the problem. Otherwise, optical issues are introduced into this scenario. In such cases, the focusing-related distortions delineated in Fig. 1b would exhibit deviations from the typical concave and convex shapes, and are difficult to be identified and restored using the SAFT-based algorithm.
-
(iii)
The estimated resolution enhancements of the proposed SAFT-based algorithm are still conservative in this study, owing to the low NA (0.125) of the applied acoustic lens. In this case, the difference in the spatial resolution and SNR between the focus and out-of-focus regions is limited. Given that our proposed SAFT-based algorithm enhances the elevational resolution in the out-of-focus regions up to the resolution at the focal point, CA-PACT systems using a focused UST array with a large NA are expected to be employed in the future to fully exploit the potential of the proposed reconstruction method, thereby maximizing the sectioning capability for high-resolution slice-stacking 3D imaging.
In the 2nd derivative BP process, we applied the re-derivative-based BP approach to weigh the high-frequency content and suppress noise and distorted signals. The variation in the lateral resolution in response to the implementation of the 2nd D-BP scheme was demonstrated. The retrieval of the deteriorated lateral resolution is clearly noticeable by comparing the CA-SAFT+ 2nd D-BP and CA-SAFT images (Figs. 7–11). Unlike the CA-SAFT algorithm, which deals with the elevational resolution, volumetric imaging considerations in different directions have been fully responded in the CA-SAFT+ 2nd D-BP approach. This is because the distribution of vascular networks consists of components with both elevational and lateral orientations, and these two components are respectively addressed by the CA-SAFT and 2nd D-BP approaches.
Compared with the original BP algorithm, the application of the 2nd D-BP method alone is suboptimal, as it diminishes the low-frequency component, which corresponds to the signals in the low resolution dimension, specifically the elevational axis. This reduction of elevational signals exacerbates the inherent resolution anisotropy between the elevational and lateral dimensions. Interestingly, when coupled with the CA-SAFT algorithm, the 2nd D-BP method demonstrates efficacy. These two techniques, CA-SAFT and 2nd D-BP, function as a two-phase restoration method and exhibit unique advantages. The unique merits of the synthesis of CA-SAFT and 2nd D-BP are demonstrated in Figs. 7–11. The comparison of the image quality between the 2nd D-BP results and CA-SAFT+ 2nd D-BP outcomes confirms the crucial role of the CA-SAFT algorithm in this strategy, which aims to reduce the highly anisotropic frequency content between the elevational and lateral dimensions by restoring the degraded elevational resolution. Without the near-isotropic feature provided by the CA-SAFT scheme, the low-frequency contents of the object corresponding to the signal perpendicular to the elevational axis tend to vanish during the signal re-derivative process in the 2nd D-BP algorithm. Therefore, the 2nd D-BP method should be integrated with the proposed CA-SAFT to demonstrate its effectiveness.
It is noteworthy that the performance of the CA-SAFT approach is inherently constrained by the in-focus resolution. To overcome this barrier, efforts could be made in the future to integrate the deconvolution strategies with the VD-based CA-SAFT approach. The deconvolution approach helps remove the influence of the system response (system resolution) and recover the original absorption distribution map. However, the deconvolution algorithm typically requires knowledge of the point spread functions (PSFs) as prior information. The acquisition of the spatial-varying PSFs along elevational dimension is very challenging because the PSFs are focal depth-dependent. Fortunately, the proposed CA-SAFT algorithm helps achieve a focal-zone-independent PSF in the elevational axis, thereby facilitating the deconvolution process because a uniformed PSF along the elevational dimension can be applied to fast restoration in the deconvolution algorithm. The integration of SAFT with the deconvolution approach holds promise for future studies because it helps further push the boundary of the elevational resolution of PACT system beyond the in-focus resolution.
Declaration of Competing Interest
The authors declare that there are no conflicts of interest.
Acknowledgements
This work was supported by National Key Research and Development Program of China (2021YFE0202200, 2022YFE0132300, 2020YFA0908800); National Natural Science Foundation of China (NSFC) Grant (62105355, 82122034, 92059108, 81927807); Chinese Academy of Sciences Grant (Youth Innovation Promotion Association 2019352, YJKYYQ20190078, GJJSTD20210003); Shenzhen Science and Technology Innovation Grant (JCYJ20220531100409023, JCYJ20210324101403010, JCYJ20220818101403008, JCYJ20200109141222892); CAS Key Laboratory of Health Informatics (2011DP173015); Guangdong Provincial Key Laboratory of Biomedical Optical Imaging (2020B121201010); Shenzhen Key Laboratory for Molecular Imaging (ZDSY20130401165820357) ; Basic and Applied Basic Research Foundation of Guangdong Province (2019A1515110727); Beijing Natural Science Foundation (7232146).
Biographies

Rongkang Gao is an Associate Professor at SIAT, CAS. She received her Ph.D. degree from the University of New South Wales, Australia, 2018. She joined SIAT in November, 2018. Dr. Gao’s research focuses on reconstruction algorithms in photoacoustics and nonlinear photoacoustic techniques.

Tao Chen is an Assistant Professor at SIAT, CAS. He received his B.S. degree in Physics from Nanjing University in 2014, and his Ph.D. degree in Condensed Matter Physics from Institute of High Energy Physics, CAS in 2019. Now his research interests focus on the development and application of photoacoustic computed tomography technology.

Yaguang Ren is an Assistant Professor at SIAT, CAS. In 2018, she got the Ph.D. degree in bioengineering at the Hong Kong University of Science and Technology. Her research interest includes the development of photoacoustic imaging, fluorescent microscope imaging and image processing.

Liangjian Liu is a PhD candidate in Optical Engineering at SIAT, CAS. Currently he is doing research on the development of high-speed photoacousitc imaging system and its applications.

Ningbo Chen is a PhD candidate in the Department of Electrical and Electronic Engineering at the University of Hong Kong. His research interests include the development of novel biomedical imaging tools based on photoacoustic imaging towards preclinical and clinical applications.

Kenneth K. Y. Wong is the Head and Professor in the Department of Electrical and Electronic Engineering in the University of Hong Kong. He received Ph.D. degree in 2003 in electrical engineering at Stanford University. His research field included novel optical generation, photonic parametric processing, ultrafast optical communications and imaging.

Liang Song is a Professor at SIAT, CAS and founding directors of The Research Lab for Biomedical Optics, and the Shenzhen Key Lab for Molecular Imaging. Prior to joining SIAT, he studied at Washington University, St. Louis and received his Ph.D. in Biomedical Engineering. His research focuses on multiple novel photoacoustic imaging technology.

Xiaohui Ma is the deputy chief surgeon of vascular surgery, and master's supervisor in Chinese PLA General Hospital. He received his doctor's degree in the Hospital. He specializes in the endovascular and surgical therapy of various vascular diseases. He focuses on the photoacoustic ultrasound research for vascular diseases.

Chengbo Liu is a Professor at SIAT, CAS. He received both his Ph.D and Bachelor degree from Xi'an Jiaotong University, each in 2012 in Biophysics and 2007 in Biomedical Engineering. During his Ph.D. training, he spent two years doing tissue spectroscopy research at Duke University as a visiting scholar. Now he is working on multi-scale photoacoustic imaging and its translational research.
Data Availability
Data will be made available upon reasonable request.
References
- 1.Wang L.V., Hu S. Photoacoustic tomography: in vivo imaging from organelles to organs. Science. 2012;vol. 335(6075):1458–1462. doi: 10.1126/science.1216210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gao R., Xu Z., Ren Y., Song L., Liu C. Nonlinear mechanisms in photoacoustics—powerful tools in photoacoustic imaging. Photoacoustics. 2021;vol. 22 doi: 10.1016/j.pacs.2021.100243. 2021/06/01/ 2021/06/01/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wang L.V., Yao J. A practical guide to photoacoustic tomography in the life sciences. Nat. Methods. 2016;vol. 13(8):627–638. doi: 10.1038/nmeth.3925. 2016/08/01. 2016/08/01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhou Yong, Yao Junjie, Lihong, Wang Tutorial on photoacoustic tomography. J. Biomed. Opt. 2016;vol. 21(6) doi: 10.1117/1.JBO.21.6.061007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhao H., Li K., Yang F., Zhou W., Chen N., Song L., Zheng C., Liu Z., Liu C. Customized anterior segment photoacoustic imaging for ophthalmic burn evaluation in vivo. Opto-Electron. Adv. 2021;vol. 4(6):200017-1–200017-9. [Google Scholar]
- 6.Pan Y., Chen N., Liu L., Liu C., Xu Z., Zhang J. Recovery of photoacoustic images based on accurate ultrasound positioning. Vis. Comput. Ind., Biomed., Art. 2021;vol. 4(1):1–7. doi: 10.1186/s42492-021-00072-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhang C., Gao R., Zhang L., Liu C., Yang Z., Zhao S. Design and synthesis of a ratiometric photoacoustic probe for in situ imaging of zinc ions in deep tissue in vivo. Anal. Chem. 2020;vol. 92(9):6382–6390. doi: 10.1021/acs.analchem.9b05431. 2020/05/05. 2020/05/05. [DOI] [PubMed] [Google Scholar]
- 8.Chen T., Liu L., Ma X., Zhang Y., Liu H., Zheng R., Ren J., Zhou H., Ren Y., Gao R. Dedicated photoacoustic imaging instrument for human periphery blood vessels: a new paradigm for understanding the vascular health. IEEE Trans. Biomed. Eng. 2021 doi: 10.1109/TBME.2021.3113764. [DOI] [PubMed] [Google Scholar]
- 9.Vu T., Li M., Humayun H., Zhou Y., Yao J. A generative adversarial network for artifact removal in photoacoustic computed tomography with a linear-array transducer. Exp. Biol. Med. 2020;vol. 245(7):597–605. doi: 10.1177/1535370220914285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Li G., Li L., Zhu L., Xia J., Wang L.V. Multiview Hilbert transformation for full-view photoacoustic computed tomography using a linear array. J. Biomed. Opt. 2015;vol. 20(6) doi: 10.1117/1.JBO.20.6.066010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li L., Xia J., Li G., Garcia-Uribe A., Sheng Q., Anastasio M.A., Wang L.V. Label-free photoacoustic tomography of whole mouse brain structures ex vivo. Neurophotonics. 2016;vol. 3(3) doi: 10.1117/1.NPh.3.3.035001. 035001-035001. 035001-035001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang D., Wang Y., Wang W., Luo D., Chitgupi U., Geng J., Zhou Y., Wang L., Lovell J.F., Xia J. Deep tissue photoacoustic computed tomography with a fast and compact laser system. Biomed. Opt. Express. 2017;vol. 8(1):112–123. doi: 10.1364/BOE.8.000112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Li L., Zhu L., Ma C., Lin L., Yao J., Wang L., Maslov K., Zhang R., Chen W., Shi J. Single-impulse panoramic photoacoustic computed tomography of small-animal whole-body dynamics at high spatiotemporal resolution. Nat. Biomed. Eng. 2017;vol. 1(5):1–11. doi: 10.1038/s41551-017-0071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Xia J., Wang L.V. Small-animal whole-body photoacoustic tomography: a review. IEEE Trans. Biomed. Eng. 2013;vol. 61(5):1380–1389. doi: 10.1109/TBME.2013.2283507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Xia J., Chatni M.R., Maslov K.I., Guo Z., Wang K., Anastasio M.A., Wang L.V. Whole-body ring-shaped confocal photoacoustic computed tomography of small animals in vivo. J. Biomed. Opt. 2012;vol. 17(5) doi: 10.1117/1.JBO.17.5.050506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Park S., Lee C., Kim J., Kim C. Acoustic resolution photoacoustic microscopy. Biomed. Eng. Lett. 2014;vol. 4(3):213–222. 2014/09/01. 2014/09/01. [Google Scholar]
- 17.Yao J., Wang L.V. Photoacoustic microscopy. Laser Photonics Rev. 2013;vol. 7(5):758–778. doi: 10.1002/lpor.201200060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cai D., Li Z., Chen S.-L. In vivo deconvolution acoustic-resolution photoacoustic microscopy in three dimensions. Biomed. Opt. Express. 2016;vol. 7(2):369–380. doi: 10.1364/BOE.7.000369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen J., Lin R., Wang H., Meng J., Zheng H., Song L. Blind-deconvolution optical-resolution photoacoustic microscopy in vivo. Opt. Express. 2013;vol. 21(6):7316–7327. doi: 10.1364/OE.21.007316. [DOI] [PubMed] [Google Scholar]
- 20.Yang C., Lan H., Gao F., Gao F. Review of deep learning for photoacoustic imaging. Photoacoustics. 2021;vol. 21 doi: 10.1016/j.pacs.2020.100215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sharma A., Pramanik M. Convolutional neural network for resolution enhancement and noise reduction in acoustic resolution photoacoustic microscopy. Biomed. Opt. Express. 2020;vol. 11(12):6826–6839. doi: 10.1364/BOE.411257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liao C.K., Li M.L., Li P.C. Optoacoustic imaging with synthetic aperture focusing and coherence weighting. Opt. Lett. 2004;vol. 29(21):2506–2508. doi: 10.1364/ol.29.002506. 2004/11/01. 2004/11/01. [DOI] [PubMed] [Google Scholar]
- 23.Li M.-L., Zhang H.F., Maslov K., Stoica G., Wang L.V. Improved in vivo photoacoustic microscopy based on a virtual-detector concept. Opt. Lett. 2006;vol. 31(4):474–476. doi: 10.1364/ol.31.000474. 2006/02/15. 2006/02/15. [DOI] [PubMed] [Google Scholar]
- 24.Deng Z., Yang X., Gong H., Luo Q. Two-dimensional synthetic-aperture focusing technique in photoacoustic microscopy. J. Appl. Phys. 2011;vol. 109(10) [Google Scholar]
- 25.Deng Z., Yang X., Gong H., Luo Q. Adaptive synthetic-aperture focusing technique for microvasculature imaging using photoacoustic microscopy. Opt. Express. 2012;vol. 20(7):7555–7563. doi: 10.1364/OE.20.007555. [DOI] [PubMed] [Google Scholar]
- 26.Turner J., Estrada H., Kneipp M., Razansky D. Improved optoacoustic microscopy through three-dimensional spatial impulse response synthetic aperture focusing technique. Opt. Lett. 2014;vol. 39(12):3390–3393. doi: 10.1364/OL.39.003390. [DOI] [PubMed] [Google Scholar]
- 27.Park J., Jeon S., Meng J., Song L., Lee J., Kim C. Delay-multiply-and-sum-based synthetic aperture focusing in photoacoustic microscopy. J. Biomed. Opt. 2016;vol. 21(3) doi: 10.1117/1.JBO.21.3.036010. [DOI] [PubMed] [Google Scholar]
- 28.Mozaffarzadeh M., Varnosfaderani M.H.H., Sharma A., Pramanik M., de Jong N., Verweij M.D. Enhanced contrast acoustic-resolution photoacoustic microscopy using double-stage delay-multiply-and-sum beamformer for vasculature imaging. J. Biophotonics. 2019;vol. 12(11) doi: 10.1002/jbio.201900133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gao R., Xue Q., Ren Y., Zhang H., Song L., Liu C. Achieving depth-independent lateral resolution in AR-PAM using the synthetic-aperture focusing technique. Photoacoustics. 2021 doi: 10.1016/j.pacs.2021.100328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cai D., Li G., Xia D., Li Z., Guo Z., Chen S.-L. Synthetic aperture focusing technique for photoacoustic endoscopy. Opt. Express. 2017;vol. 25(17):20162–20171. doi: 10.1364/OE.25.020162. [DOI] [PubMed] [Google Scholar]
- 31.C. Sheaff, S. Ashkenazi, "A fiber optic optoacoustic ultrasound sensor for photoacoustic endoscopy." pp. 2135–2138.
- 32.Xia J., Guo Z., Maslov K., Aguirre A., Zhu Q., Percival C., Wang L.V. Three-dimensional photoacoustic tomography based on the focal-line concept. J. Biomed. Opt. 2011;vol. 16(9) doi: 10.1117/1.3625576. 090505-090505-3. 090505-090505-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Yoon C., Kang J., Song T.-k, Chang J.H. Elevational synthetic aperture focusing for three-dimensional photoacoustic imaging using a clinical one-dimensional array transducer. IEEE Trans. Biomed. Eng. 2022;vol. 69(9):2817–2825. doi: 10.1109/TBME.2022.3154754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Vaithilingam S., Ma T.-J., Furukawa Y., Wygant I.O., Zhuang X., De La Zerda A., Oralkan O., Kamaya A., Jeffrey R.B., Khuri-Yakub B.T. Three-dimensional photoacoustic imaging using a two-dimensional CMUT array. IEEE Trans. Ultrason., Ferroelectr., Freq. Control. 2009;vol. 56(11):2411–2419. doi: 10.1109/TUFFc.2009.1329. [DOI] [PubMed] [Google Scholar]
- 35.Spadin F., Jaeger M., Nuster R., Subochev P., Frenz M. Quantitative comparison of frequency-domain and delay-and-sum optoacoustic image reconstruction including the effect of coherence factor weighting. Photoacoustics. 2020;vol. 17 doi: 10.1016/j.pacs.2019.100149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Amjadian M., Mostafavi S.M., Chen J., Kavehvash Z., Zhu J., Wang L. Super-resolution photoacoustic microscopy using structured-illumination. IEEE Trans. Med. Imaging. 2021 doi: 10.1109/TMI.2021.3073555. [DOI] [PubMed] [Google Scholar]
- 37.K.W. Hollman, K.W. Rigby and M.O. Donnell, "Coherence factor of speckle from a multi-row probe." pp. 1257–1260 vol.2.
- 38.Mozaffarzadeh M., Makkiabadi B., Basij M., Mehrmohammadi M. Image improvement in linear-array photoacoustic imaging using high resolution coherence factor weighting technique. BMC Biomed. Eng. 2019;vol. 1(1):10. doi: 10.1186/s42490-019-0009-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cai D., Li Z., Li Y., Guo Z., Chen S.-L. Photoacoustic microscopy in vivo using synthetic-aperture focusing technique combined with three-dimensional deconvolution. Opt. Express. 2017;vol. 25(2):1421–1434. doi: 10.1364/OE.25.001421. [DOI] [PubMed] [Google Scholar]
- 40.Xu M., Wang L.V. Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. E. 2005;vol. 71(1) doi: 10.1103/PhysRevE.71.016706. 01/19/ 01/19/ [DOI] [PubMed] [Google Scholar]
- 41.Cho S., Baik J., Managuli R., Kim C. 3D PHOVIS: 3D photoacoustic visualization studio. Photoacoustics. 2020;vol. 18 doi: 10.1016/j.pacs.2020.100168. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available upon reasonable request.