ABSTRACT
Fractional quantization can emerge in noncorrelated systems due to the parity anomaly, while its condensed matter realization is a challenging problem. We propose that in axion insulators (AIs), parity anomaly manifests a unique fractional boundary excitation: the half-quantized helical hinge currents. These helical hinge currents microscopically originate from the lateral Goos-Hänchen (GH) shift of massless side-surface Dirac electrons that are totally reflected from the hinges. Meanwhile, due to the presence of the massive top and bottom surfaces of the AI, the helical current induced by the GH shift is half-quantized. The semiclassical wave packet analysis uncovers that the hinge current has a topological origin and its half quantization is robust to parameter variations. Lastly, we propose an experimentally feasible six-terminal device to identify the half-quantized hinge channels by measuring the nonreciprocal conductances. Our results advance the realization of the half-quantization and topological magnetoelectric responses in AIs.
Keywords: axion insulator, parity anomaly, half-quantization, Goos-Hänchen effect, topological magnetoelectric effect
Half-quantized helical hinge current, which originates from the topological literal shift of electrons on the metallic side surface, serves as the fingerprint signature of the axion insulator.
INTRODUCTION
Fractional quantization in condensed matter materials is usually accompanied by the emergence of quasi-particles driven by strong correlations. A prominent example is the fractional quantum Hall effect [1–3], which is the fairyland of fractionally charged quasi-particle excitations, and has attracted intense attention in the condensed matter community since its discovery. Interestingly, fractional quantization can also emerge in noncorrelated systems. Such a fractional quantization is triggered by parity anomaly [4–6], which generates a parity-violating current with the half-integer-quantized Hall conductance. However, realizing the parity anomaly in (2+1) dimensions and observing the half-quantized transport signals in condensed matter systems have been challenging problems for over 40 years [7–11]. A critical issue is that the bulk-boundary correspondence principle implies that some kind of half-quantized boundary excitations should exist in the parity anomaly systems. Unfortunately, the physical picture of such excitations, their material realization and the roadmap of their experimental characterization are elusive.
Encouragingly, the axion insulator (AI) [12–15] provides an ideal platform to realize parity anomaly on its top and bottom surfaces [16–18]. As a nontrivial topological phase, the AI manifests a unique topological magnetoelectric (TME) effect [15,19–24] and has stimulated extensive research interests [25–48]. Experimentally, the zero Hall conductance plateau has been observed in magnetic topological insulator (TI) heterostructures [28–30] and the antiferromagnetic TI 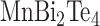 [33]. However, the zero Hall plateau cannot provide smoking-gun evidence of the AI, and, more importantly, parity-anomaly-induced half-quantized signals in AIs have not been observed. Such a dilemma originates from shallow knowledge of the boundary excitations in AIs. To give a definitive answer, a concrete and in-depth understanding of the parity-anomaly-induced boundary excitations in the AI is highly desirable.
[33]. However, the zero Hall plateau cannot provide smoking-gun evidence of the AI, and, more importantly, parity-anomaly-induced half-quantized signals in AIs have not been observed. Such a dilemma originates from shallow knowledge of the boundary excitations in AIs. To give a definitive answer, a concrete and in-depth understanding of the parity-anomaly-induced boundary excitations in the AI is highly desirable.
In this work, we find that parity anomaly in AIs induces a unique boundary excitation: the half-quantized helical hinge currents. Based on the semiclassical wave packet dynamics, we establish the microscopic picture of these hinge currents. We proposed that the massless Dirac electrons on the side surfaces of the AI undergo a lateral Goos-Hänchen (GH) shift when they are reflected from the massive top or bottom surface (see Fig. 1), reminiscent of the GH shift [49–53] of the totally reflected light beam. Moreover, due to the breaking of time-reversal (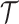 ) symmetry, the GH shift favors a specific direction on the hinge. Consequently, helical GH shift currents accumulate on the hinges of the AI when side-surface electrons bounce back and forth between the gapped top and bottom surfaces (see Fig. 1(a) and (b)), which is distinct from the chiral net currents on the edge of the Chern insulator (CI) (see Fig. 1(c)). Interestingly, we find that the differential GH shift current δIGH is exactly half-quantized with respect to the differential Fermi energy δEF, i.e. δIGH = eδEF/2h. We demonstrate that the GH shift current originates from the nonvanishing Berry curvature during the scattering process, and its half-quantization is robust to the variation of parameters. Then, we numerically verify the half-quantized helical hinge currents through a three-dimensional (3D) lattice model. Finally, we propose a six-terminal device to identify the half-quantized hinge currents in the AI by measuring the nonreciprocal conductances.
) symmetry, the GH shift favors a specific direction on the hinge. Consequently, helical GH shift currents accumulate on the hinges of the AI when side-surface electrons bounce back and forth between the gapped top and bottom surfaces (see Fig. 1(a) and (b)), which is distinct from the chiral net currents on the edge of the Chern insulator (CI) (see Fig. 1(c)). Interestingly, we find that the differential GH shift current δIGH is exactly half-quantized with respect to the differential Fermi energy δEF, i.e. δIGH = eδEF/2h. We demonstrate that the GH shift current originates from the nonvanishing Berry curvature during the scattering process, and its half-quantization is robust to the variation of parameters. Then, we numerically verify the half-quantized helical hinge currents through a three-dimensional (3D) lattice model. Finally, we propose a six-terminal device to identify the half-quantized hinge currents in the AI by measuring the nonreciprocal conductances.
Figure 1.
Schematics of the half-quantized hinge currents. Half-quantized hinge currents originate from the GH shift currents of side-surface electrons that bounce back and forth between gapped top and bottom surfaces in the AI (a) and the CI (c). (b) Unfolded view of the top, side and bottom surfaces of the AI. The trajectory of a massless electron illustrates the formation of the GH shift current IGH. When the contributions from all the electrons are considered, the trajectory segments on the hinges are merged together, leading to net helical hinge currents.
MODEL HAMILTONIAN AND THE GOOS-HÄNCHEN SHIFT
To begin with, we model the AI by a 3D magnetic TI, of which the top and bottom surfaces are gapped oppositely while the side surfaces remain gapless. Such a model is in accordance with the experimental setups utilized to realize the AI state in magnetic TI heterostructures or the antiferromagnetic TI 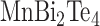 [28–30,33]. According to the bulk-boundary correspondence theorem, the top/bottom surface and the side surface of the AI can be described by the 2D effective Hamiltonians
[28–30,33]. According to the bulk-boundary correspondence theorem, the top/bottom surface and the side surface of the AI can be described by the 2D effective Hamiltonians
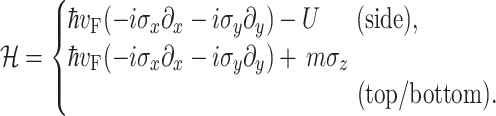 |
(1) |
Here, vF denotes the Fermi velocity, U is the gate potential and m is the mass term induced by the magnetization. In the following discussions, we unfold the top, side and bottom surfaces of the AI (see Fig. 1(a)) into the x-y plane (see Fig. 1(b)).
We use the probability flux method (see [51,52] and the online supplementary material) to calculate the GH shift on the hinge of the AI. As shown in Fig. 2(a), we place the massless side surface in x ≤ 0 and the massive top/bottom surface in x > 0. Firstly, we solve the scattering problem by matching 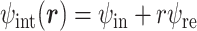 (x ≤ 0) and
(x ≤ 0) and 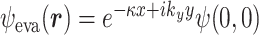 (x > 0) at x = 0, where
(x > 0) at x = 0, where 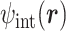 is the interference superposition of the incident plane wave
is the interference superposition of the incident plane wave  and reflected plane wave
and reflected plane wave 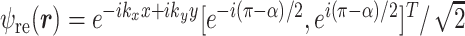 in the massless region. Here
in the massless region. Here 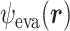 is the evanescent wave in the massive region, α = arctan(ky/kx) denotes the incident angle (see Fig. 2(a)) and
is the evanescent wave in the massive region, α = arctan(ky/kx) denotes the incident angle (see Fig. 2(a)) and  . Here we only consider the total reflection process, which captures the physics within the magnetization gap. The reflection coefficient
. Here we only consider the total reflection process, which captures the physics within the magnetization gap. The reflection coefficient  is given in the online supplementary material. Then, imagine that the incident and reflected waves have finite width, as depicted in Fig. 2(a); the GH shift can be obtained under the probability flux conservation constraint. As labeled in Fig. 2(a), Jint, Jeva and JGH represent the fluxes carried by the interference wave, the evanescent wave and the part proportional to the GH shift. We denote by Jd the flux through the cross section colored blue with width d. Suppose that the probability density of the incident/reflected beam is normalized as
is given in the online supplementary material. Then, imagine that the incident and reflected waves have finite width, as depicted in Fig. 2(a); the GH shift can be obtained under the probability flux conservation constraint. As labeled in Fig. 2(a), Jint, Jeva and JGH represent the fluxes carried by the interference wave, the evanescent wave and the part proportional to the GH shift. We denote by Jd the flux through the cross section colored blue with width d. Suppose that the probability density of the incident/reflected beam is normalized as 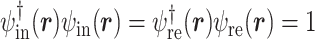 ; then
; then
Figure 2.
Microscopic mechanism of the hinge currents due to the GH shift. (a) Sketch of the scattering process on the hinge, where a beam of massless Dirac electrons is totally reflected from a massive barrier. (b) The GH shift versus α with U = 1, m = 0.1 and E = 0. The upper panel shows the total GH shift ΔGH and the lower panel shows its contributions from the evanescent wave (ΔGH,eva) and the interference wave (ΔGH,int). (c) Reflection phase difference versus α for different m. The inset shows the evanescent wave and interference wave contributions to δIGH (in units of eδEF/h) versus m.
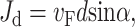 |
(2a) |
 |
(2b) |
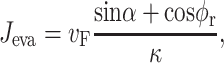 |
(2c) |
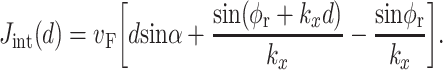 |
(2d) |
The flux conservation condition imposes that Jint + Jeva = JGH + Jd. The GH shift as a function of d reads
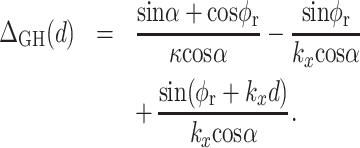 |
(3) |
In the semiclassical limit, the d dependence of ΔGH(d) can be averaged out, resulting in the net GH shift
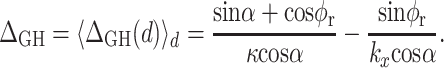 |
(4) |
In the upper panel of Fig. 2(b), we plot ΔGH as a function of the incident angle α with fixed E, U and m. For glancing incidence, i.e. α → ±π/2, ΔGH diverges but with opposite sign for α = π/2 and α = −π/2. Such behavior indicates that at large incident angles the GH shift has the same direction as the incident wave, and thus does not show the chiral feature. However, ΔGH peaks for vertical incidence, i.e. α → 0, clearly showing that the GH shift favors a specific direction and manifests the chiral feature. The chiral ΔGH further implies that the net GH shift current accumulated on the hinge is chiral. We then decompose ΔGH according to its contributions from the evanescent wave ΔGH,eva and the interference wave ΔGH,int. As will be discussed later, ΔGH,eva and ΔGH,int introduce the components of the shift current with different decay laws. The lower panel of Fig. 2(b) shows that the chiral part of ΔGH is mostly carried by ΔGH,eva, which lies on the  -symmetry-broken top/bottom surface of the AI. In contrast, the nonchiral part, especially for glancing incidence α → ±π/2, is mostly carried by ΔGH,int.
-symmetry-broken top/bottom surface of the AI. In contrast, the nonchiral part, especially for glancing incidence α → ±π/2, is mostly carried by ΔGH,int.
HALF-QUANTIZED SHIFT CURRENT
To give a microscopic picture of the chiral hinge current induced by the GH shift, we consider the electron in the scattering problem as a point particle, which bounces back and forth between double massive barriers as sketched in Fig. 1(b). Suppose that the width between the opposite hinges is Lx; thus, the average time interval between two consecutive bounces is 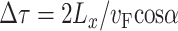 for −π/2 < α < π/2. When it bounces off the hinge, it undergoes a lateral GH shift ΔGH. Such a lateral shift induces an anomalous velocity of electrons along the hinge as
for −π/2 < α < π/2. When it bounces off the hinge, it undergoes a lateral GH shift ΔGH. Such a lateral shift induces an anomalous velocity of electrons along the hinge as
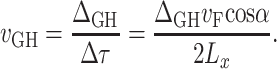 |
(5) |
The total GH shift current induced by vGH is obtained by counting the contributions of all filled electrons as
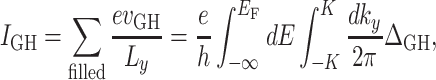 |
(6) |
where Ly is the circumference of the side surface and K = (E + U)/ℏvF is the Fermi wave vector at energy E. Details of the calculations can be found in the online supplementary material. By employing the stationary phase method (see [50,54–56] and the online supplementary material), we find that the GH shift can be written as ΔGH = −∂φr/∂ky. Substituting this result into (6), we obtain the differential shift current δIGH = δEF[φr(−π/2) − φr(π/2)]e/2πh.
In Fig. 2(c), we plot φr as a function of α for different m. It is clear that φr(−π/2) − φr(π/2) = π and robust to the variation of m (see the online supplementary material). Therefore, δIGH is exactly half-quantized with respect to δEF as
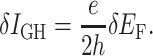 |
(7) |
Moreover, δIGH can be decomposed according to its contributions from the evanescent wave and the interference wave, i.e. δIGH = δIGH, eva + δIGH,int. We emphasize that δIGH,int shows a power-law (x−1/2) decay from the hinge, while δIGH,eva decays exponentially from the hinge (e−x/λ); see the online supplementary material. Therefore, δIGH is different from the current carried by the topologically protected edge or hinge state, which decays exponentially on both sides of the hinge. The inset of Fig. 2(c) plots δIGH,eva and δIGH,int versus m. The differential shift current δIGH is mainly contributed from δIGH,eva when m is small. As m increases, the contribution from δIGH,int becomes dominant.
TOPOLOGICAL ORIGIN OF THE HALF QUANTIZATION
We provide a topological viewpoint of the half-quantized GH shift current in the frame of adiabatic charge transport theory [57–60]. Here, we use Hamiltonian 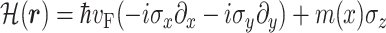 to describe the scattering process, where m(x) is a smooth function connecting the gapless and the gapped regions with m(x) → m for x ≫ 0 and m(x) → 0 for x ≪ 0 (see Fig. 3(a)). During the reflection process, the energy E and momentum ky are conserved. Therefore, the relation
to describe the scattering process, where m(x) is a smooth function connecting the gapless and the gapped regions with m(x) → m for x ≫ 0 and m(x) → 0 for x ≪ 0 (see Fig. 3(a)). During the reflection process, the energy E and momentum ky are conserved. Therefore, the relation 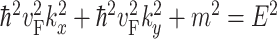 holds. We take t = −ℏvFkx as the virtual time and the scattering process is now described by the time-dependent 1D Hamiltonian H(ky, t) = −tσx + ℏvFkyσy + m(t)σz, which describes the Zeeman coupling of a Pauli spinor to a time-dependent magnetic field
holds. We take t = −ℏvFkx as the virtual time and the scattering process is now described by the time-dependent 1D Hamiltonian H(ky, t) = −tσx + ℏvFkyσy + m(t)σz, which describes the Zeeman coupling of a Pauli spinor to a time-dependent magnetic field 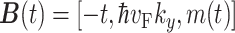 (see Fig. 3(b)). The study of the GH shift is reduced to the study of an adiabatic charge transport problem in the y direction, with an internal adiabatic spin procession under the magnetic field
(see Fig. 3(b)). The study of the GH shift is reduced to the study of an adiabatic charge transport problem in the y direction, with an internal adiabatic spin procession under the magnetic field 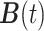 [61].
[61].
Figure 3.
Topological origin of the half-quantized GH shift current. (a) Sketch of the process where a wave packet of a massless Dirac electron bounces off a massive barrier, undergoing a lateral GH shift in the y direction. (b) Sketch of the reflection process of the wave packet in the momentum space where ky is unchanged due to the translation symmetry in the y direction. During the reflection the energy E is conserved; therefore, kx and the mass m of the local Hamiltonian are varying under the constraint 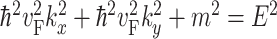 . Such a reflection process can also be understood as the 1D charge transport problem in the y direction when we take t = −ℏvFkx as the virtual time. The effective time-dependent Hamiltonian can be viewed as a Zeeman type
. Such a reflection process can also be understood as the 1D charge transport problem in the y direction when we take t = −ℏvFkx as the virtual time. The effective time-dependent Hamiltonian can be viewed as a Zeeman type 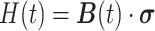 with
with 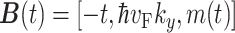 and the reflection process is simplified to an adiabatic spin procession for fixed ky and E. (c) Sketch of the adiabatic charge transport in the y direction. The nontrivial Berry curvature
and the reflection process is simplified to an adiabatic spin procession for fixed ky and E. (c) Sketch of the adiabatic charge transport in the y direction. The nontrivial Berry curvature  induces an anomalous velocity v(ky) in the y direction. After the reflection, the total contribution from the adiabatic current gives rise to the GH shift.
induces an anomalous velocity v(ky) in the y direction. After the reflection, the total contribution from the adiabatic current gives rise to the GH shift.
The instantaneous eigenstates of H(ky, t) are  , where ‘±’ denotes the spin-up and spin-down components of the spinor. Following the analysis in [60], up to first order in the rate of change in the Hamiltonian, the wave function is given by
, where ‘±’ denotes the spin-up and spin-down components of the spinor. Following the analysis in [60], up to first order in the rate of change in the Hamiltonian, the wave function is given by
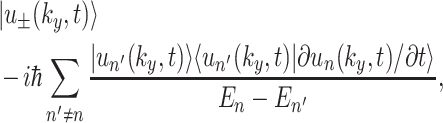 |
(8) |
where n(n′) = ± represents the spin-up or spin-down components. The average velocity for a given ky is, to first order,
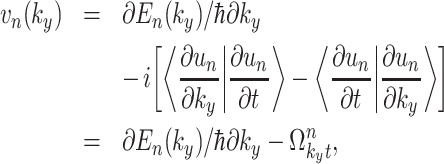 |
(9) |
where 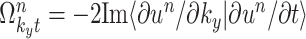 is the Berry curvature in ky-t space. We only consider the conduction band with n = + where the scattering process happens; thus, from now on we omit the band index n. The GH shift (see Fig. 3(c)) in the y direction contributed from a given ky is
is the Berry curvature in ky-t space. We only consider the conduction band with n = + where the scattering process happens; thus, from now on we omit the band index n. The GH shift (see Fig. 3(c)) in the y direction contributed from a given ky is
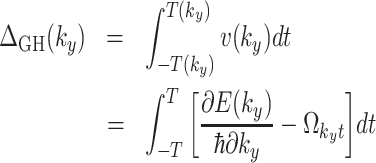 |
(10) |
with  . Combining this with (6), one obtains
. Combining this with (6), one obtains
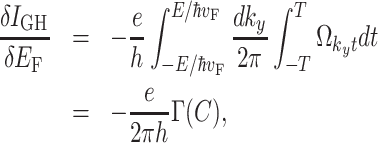 |
(11) |
where Γ(C) is the Berry phase along boundary C of the integration manifold. The integration of ∂E(ky)/ℏ∂ky vanishes because the band structure is symmetric with respect to ky.
Intuitively, Γ(C) = ±π due to the gapless Dirac electrons on the side surfaces of the AI. To pin down the sign of Γ(C), and hence the direction of the differential GH shift current, we perform the integral in polar coordinates. Define 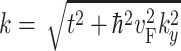 , t = kcosθ and ℏvFky = ksinθ. The Berry curvature under the polar coordinate system becomes
, t = kcosθ and ℏvFky = ksinθ. The Berry curvature under the polar coordinate system becomes 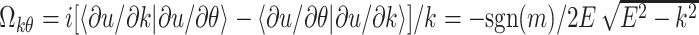 with
with 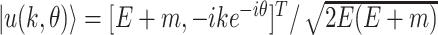 . The Berry phase
. The Berry phase
 |
(12) |
Therefore, we conclude that the half-quantized chiral GH shift current δIGH/δEF = sgn(m)e/2h is protected by the π Berry phase of the massless Dirac electron while its direction is determined by the mass m of the massive barrier.
VISUALIZING THE HALF-QUANTIZED HINGE CURRENT DISTRIBUTION
The half-quantized hinge current can be numerically visualized based on the 3D magnetic TI Hamiltonian. The model Hamiltonian is given by H = H0 + HM, where H0 = ∑i=x, y, zAkiτx ⊗ σi + (M0 − Bk2)τz ⊗ σ0 is the nonmagnetic part and 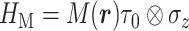 represents the magnetization term [62,63]. Here, σi and τi are the Pauli matrices acting on the spin and orbital spaces, respectively. The current density [16] in the y direction across the x-z plane with
represents the magnetization term [62,63]. Here, σi and τi are the Pauli matrices acting on the spin and orbital spaces, respectively. The current density [16] in the y direction across the x-z plane with 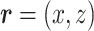 is
is
 |
(13) |
where 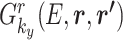 is the retarded Green’s function for the momentum-sliced Hamiltonian H(ky).
is the retarded Green’s function for the momentum-sliced Hamiltonian H(ky).
We first evaluate a semimagnetic TI with a gapped top surface in the y-z plane, which can be viewed as ‘half’ of an AI (see Fig. 4(a)) [39,40,64]. As shown in Fig. 4(b), the current flux 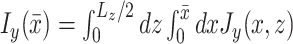 oscillates around 0.5. The
oscillates around 0.5. The  averaged
averaged 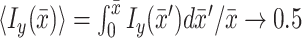 clearly shows the half-quantization of the chiral hinge current, which coincides with the GH shift analysis. For an AI where the top and bottom surfaces are gapped with opposite magnetization (see Fig. 4(c) and (d)), a pair of counterpropagating hinge currents emerges on the hinges. The moving averaged current flux
clearly shows the half-quantization of the chiral hinge current, which coincides with the GH shift analysis. For an AI where the top and bottom surfaces are gapped with opposite magnetization (see Fig. 4(c) and (d)), a pair of counterpropagating hinge currents emerges on the hinges. The moving averaged current flux 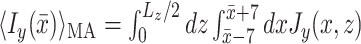 further demonstrates that the hinge currents are nearly half-quantized and helical.
further demonstrates that the hinge currents are nearly half-quantized and helical.
Figure 4.

Current density distribution for semimagnetic TI and AI. (a),(c) Schematics of semimagnetic TI and AI (infinite in the y direction). The thickness in the z direction is Lz = 8. The pink areas in (a) and (c) show the region (0 ≤ z ≤ Lz/2) and the dotted box in (c) shows the cross section in the x-z plane. (b) The current flux through region 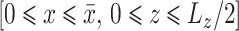 and
and 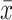 averaged
averaged 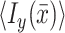 for semimagnetic TI. (d) The upper panel shows the distribution of Jy(x, z) in the x-z plane. The lower panel shows the moving averaged current flux
for semimagnetic TI. (d) The upper panel shows the distribution of Jy(x, z) in the x-z plane. The lower panel shows the moving averaged current flux 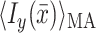 through the window
through the window 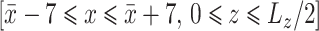 . Both Jy and Iy are in units of e/h.
. Both Jy and Iy are in units of e/h.
EXPERIMENTAL CHARACTERIZATION OF THE HALF-QUANTIZED HELICAL HINGE CURRENTS
The half-quantized hinge current δIGH can be experimentally detected by a six-terminal device, as illustrated in Fig. 5(a). Leads 1 and 3 (2 and 4) are contacted near the top (bottom) surface of the AI, while leads 5 and 6 are contacted to the ends of the sample. According to the Landauer-Büttiker formula, the transmission coefficient between terminals i and j is Tij = Tr[ΓiGrΓjGa] and the related differential conductance is Gij = e2/h · Tij [65–68]. The measurement method of Gij is given in the online supplementary material. Here Γi is the linewidth function of lead i and Gr(a) is the retarded (advanced) Green’s function of the AI sample.
Figure 5.

Experimental characterization of the half-quantized helical hinge currents by the nonreciprocal conductance. (a) Schematic of the six-terminal device. Leads 5 and 6 contact to the ends of the AI film. Terminals 1–4 are surface leads with 1 and 3 (2 and 4) contacted near the top (bottom) surface. (b) Local current distribution of the AI. (c) Nonreciprocal conductance 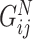 between lead i and lead j as a function of EF. (d) Schematic illustration of the relationship between the quantized TME response and the half-quantized helical hinge currents. Here
between lead i and lead j as a function of EF. (d) Schematic illustration of the relationship between the quantized TME response and the half-quantized helical hinge currents. Here 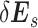 is the interface electric field and
is the interface electric field and 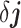 is the hinge current.
is the hinge current.
To demonstrate the existence of the helical hinge channels, we calculate the nonreciprocal conductance 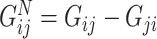 between lead i and lead j. As shown in Fig. 5(c), in the AI state
between lead i and lead j. As shown in Fig. 5(c), in the AI state 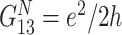 and
and 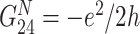 are half-quantized with opposite signs and
are half-quantized with opposite signs and 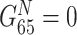 . This implies that there exist two counterpropagating half-quantized hinge channels. Moreover, the spatial distribution of the local current Ji → j(E) from site i to j [69] further reveals the helical signature of the transport hinge currents in the AI, as shown in Fig. 5(b). Since the nonreciprocal conductance
. This implies that there exist two counterpropagating half-quantized hinge channels. Moreover, the spatial distribution of the local current Ji → j(E) from site i to j [69] further reveals the helical signature of the transport hinge currents in the AI, as shown in Fig. 5(b). Since the nonreciprocal conductance 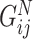 counts the asymmetric part of Ji → j(E), we can deduce that the half-quantized conducting channel originates from the half-quantized chiral GH shift current δIGH on the hinge of the AI. The results are well consistent with those determined from the GH shift (see Fig. 2) as well as the current density distribution (see Fig. 4). Therefore, these transport signals strongly confirm the reliability of the microscopic picture of half-quantized hinge currents proposed in Fig. 1. Since the half-quantized helical hinge currents serve as a fingerprint of the AI, our proposals also promote the experimental identification of AIs.
counts the asymmetric part of Ji → j(E), we can deduce that the half-quantized conducting channel originates from the half-quantized chiral GH shift current δIGH on the hinge of the AI. The results are well consistent with those determined from the GH shift (see Fig. 2) as well as the current density distribution (see Fig. 4). Therefore, these transport signals strongly confirm the reliability of the microscopic picture of half-quantized hinge currents proposed in Fig. 1. Since the half-quantized helical hinge currents serve as a fingerprint of the AI, our proposals also promote the experimental identification of AIs.
DISCUSSION
The half-quantized helical hinge currents can be understood as a consequence of the quantized TME response in the AI [15]. As sketched in Fig. 5(d), a shift of the Fermi energy on the surfaces of the AI induces an interface electric field 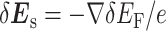 . According to Maxwell’s equations with the axion term,
. According to Maxwell’s equations with the axion term, 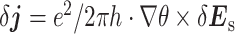 [15,70] with the spatially varying axion angle θ. The half-quantized hinge current δI = ±eδEF/2h is obtained by integrating
[15,70] with the spatially varying axion angle θ. The half-quantized hinge current δI = ±eδEF/2h is obtained by integrating 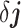 over the corner.
over the corner.
In conclusion, we found that the half-quantized helical hinge currents exist in AIs, and established their microscopic picture based on GH shift currents. The half-quantization of the GH shift current has a topological origin and is robust to the variation of parameters. We numerically demonstrated that the half-quantized hinge channel is reflected by the half-quantized nonreciprocal conductances. Our studies deepen the perception of the boundary excitations of the AI and shed light on the detection of AIs through transport experiments.
METHODS
Derivation of the cross-section current density
In calculating the cross-section current density, we take the system to be infinite in the y direction. The cross section in the x-z plane is finite in the x and y directions for the AI and the CI, and semi-infinite in the x direction for the semimagnetic TI. Since the Hamiltonian is infinite in the y direction for the three cases, ky is a good quantum number and the total Hamiltonian H can be decomposed into summations of the momentum-sliced Hamiltonians as
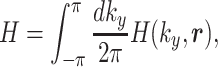 |
(14) |
where  is the momentum-sliced Hamiltonian with momentum ky and
is the momentum-sliced Hamiltonian with momentum ky and 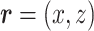 . We define Green’s function
. We define Green’s function 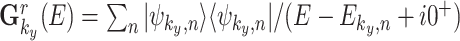 , where |ψn〉 is the nth eigenstate of
, where |ψn〉 is the nth eigenstate of 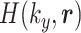 . We write
. We write 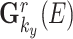 in real-space form as
in real-space form as  .
.
The velocity operator in the y direction for a given ky is 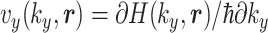 . The local current density in the x-z plane can be expressed as
. The local current density in the x-z plane can be expressed as
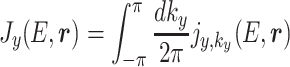 |
(15) |
with the local current density for a given ky given by
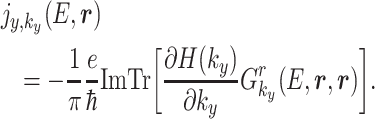 |
(16) |
Equation (16) can be derived as follows:
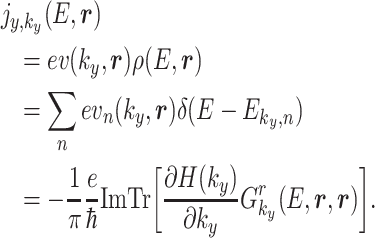 |
(17) |
Here 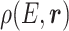 is the local density of states at energy E and position
is the local density of states at energy E and position  , which can be expanded as
, which can be expanded as 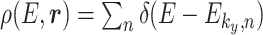 .
.
Supplementary Material
Contributor Information
Ming Gong, International Center for Quantum Materials, School of Physics, Peking University, Beijing 100871, China.
Haiwen Liu, Center for Advanced Quantum Studies, Department of Physics, Beijing Normal University, Beijing 100875, China.
Hua Jiang, School of Physical Science and Technology, Soochow University, Suzhou 215006, China; Institute for Advanced Study, Soochow University, Suzhou 215006, China.
Chui-Zhen Chen, School of Physical Science and Technology, Soochow University, Suzhou 215006, China; Institute for Advanced Study, Soochow University, Suzhou 215006, China.
X-C Xie, International Center for Quantum Materials, School of Physics, Peking University, Beijing 100871, China; CAS Center for Excellence in Topological Quantum Computation, University of Chinese Academy of Sciences, Beijing 100190, China.
ACKNOWLEDGEMENTS
The authors thank Qian Niu, Qingfeng Sun and Zhida Song for fruitful discussions.
FUNDING
This work was financially supported by the National Key R&D Program of China (2022YFA1403700, 2019YFA0308403 and 2015CB921102), the National Natural Science Foundation of China (11974256), the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB28000000).
AUTHOR CONTRIBUTIONS
X.-C.X. conceived the idea from a discussion with H.L.; X.-C.X. supervised the research with H.J.; C.-Z.C. and M.G. performed the analytical and numerical calculations. All authors co-wrote the manuscript.
Conflict of interest statement. None declared.
REFERENCES
- 1. Tsui DC, Stormer HL, Gossard AC. Two-dimensional magnetotransport in the extreme quantum limit. Phys Rev Lett 1982; 48: 1559–62. 10.1103/PhysRevLett.48.1559 [DOI] [Google Scholar]
- 2. Laughlin RB. Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations. Phys Rev Lett 1983; 50: 1395–8. 10.1103/PhysRevLett.50.1395 [DOI] [Google Scholar]
- 3. Stormer HL. Nobel lecture: the fractional quantum Hall effect. Rev Mod Phys 1999; 71: 875–89. 10.1103/RevModPhys.71.875 [DOI] [Google Scholar]
- 4. Niemi AJ, Semenoff GW. Axial-anomaly-induced fermion fractionization and effective gauge-theory actions in odd-dimensional space-times. Phys Rev Lett 1983; 51: 2077–80. 10.1103/PhysRevLett.51.2077 [DOI] [Google Scholar]
- 5. Redlich AN. Gauge noninvariance and parity nonconservation of three-dimensional fermions. Phys Rev Lett 1984; 52: 18–21. 10.1103/PhysRevLett.52.18 [DOI] [Google Scholar]
- 6. Jackiw R. Fractional charge and zero modes for planar systems in a magnetic field. Phys Rev D 1984; 29: 2375–7. 10.1103/PhysRevD.29.2375 [DOI] [PubMed] [Google Scholar]
- 7. Semenoff GW. Condensed-matter simulation of a three-dimensional anomaly. Phys Rev Lett 1984; 53: 2449–52. 10.1103/PhysRevLett.53.2449 [DOI] [Google Scholar]
- 8. Fradkin E, Dagotto E, Boyanovsky D. Physical realization of the parity anomaly in condensed matter physics. Phys Rev Lett 1986; 57: 2967–70. 10.1103/PhysRevLett.57.2967 [DOI] [PubMed] [Google Scholar]
- 9. Xu Y, Miotkowski I, Liu Cet al. Observation of topological surface state quantum Hall effect in an intrinsic three-dimensional topological insulator. Nat Phys 2014; 10: 956–63. 10.1038/nphys3140 [DOI] [Google Scholar]
- 10. Xu Y, Miotkowski I, Chen YP. Quantum transport of two-species Dirac fermions in dual-gated three-dimensional topological insulators. Nat Commun 2016; 7: 11434. 10.1038/ncomms11434 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Zhang S, Pi L, Wang Ret al. Anomalous quantization trajectory and parity anomaly in Co cluster decorated BiSbTeSe2 nanodevices. Nat Commun 2017; 8: 977. 10.1038/s41467-017-01065-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Peccei RD, Quinn HR. CP conservation in the presence of pseudoparticles. Phys Rev Lett 1977; 38: 1440–3. 10.1103/PhysRevLett.38.1440 [DOI] [Google Scholar]
- 13. Peccei RD, Quinn HR. Constraints imposed by CP conservation in the presence of pseudoparticles. Phys Rev D 1977; 16: 1791–7. 10.1103/PhysRevD.16.1791 [DOI] [Google Scholar]
- 14. Wilczek F. Two applications of axion electrodynamics. Phys Rev Lett 1987; 58: 1799–802. 10.1103/PhysRevLett.58.1799 [DOI] [PubMed] [Google Scholar]
- 15. Qi XL, Hughes TL, Zhang SC. Topological field theory of time-reversal invariant insulators. Phys Rev B 2008; 78: 195424. 10.1103/PhysRevB.78.195424 [DOI] [Google Scholar]
- 16. Chu RL, Shi J, Shen SQ. Surface edge state and half-quantized Hall conductance in topological insulators. Phys Rev B 2011; 84: 085312. 10.1103/PhysRevB.84.085312 [DOI] [Google Scholar]
- 17. Varnava N, Vanderbilt D. Surfaces of axion insulators. Phys Rev B 2018; 98: 245117. 10.1103/PhysRevB.98.245117 [DOI] [Google Scholar]
- 18. Gu M, Li J, Sun Het al. Spectral signatures of the surface anomalous Hall effect in magnetic axion insulators. Nat Commun 2021; 12: 3524. 10.1038/s41467-021-23844-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Essin AM, Moore JE, Vanderbilt D. Magnetoelectric polarizability and axion electrodynamics in crystalline insulators. Phys Rev Lett 2009; 102: 146805. 10.1103/PhysRevLett.102.146805 [DOI] [PubMed] [Google Scholar]
- 20. Qi XL, Li R, Zang Jet al. Inducing a magnetic monopole with topological surface states. Science 2009; 323: 1184–7. 10.1126/science.1167747 [DOI] [PubMed] [Google Scholar]
- 21. Li R, Wang J, Qi XLet al. Dynamical axion field in topological magnetic insulators. Nat Phys 2010; 6: 284–8. 10.1038/nphys1534 [DOI] [Google Scholar]
- 22. Ooguri H, Oshikawa M. Instability in magnetic materials with a dynamical axion field. Phys Rev Lett 2012; 108: 161803. 10.1103/PhysRevLett.108.161803 [DOI] [PubMed] [Google Scholar]
- 23. Olsen T, Taherinejad M, Vanderbilt Det al. Surface theorem for the Chern-Simons axion coupling. Phys Rev B 2017; 95: 075137. 10.1103/PhysRevB.95.075137 [DOI] [PubMed] [Google Scholar]
- 24. Sekine A, Nomura K. Axion electrodynamics in topological materials. J. Appl. Phys. 2021; 129: 141101. 10.1063/5.0038804 [DOI] [Google Scholar]
- 25. Taherinejad M, Vanderbilt D. Adiabatic pumping of Chern-Simons axion coupling. Phys Rev Lett 2015; 114: 096401. 10.1103/PhysRevLett.114.096401 [DOI] [PubMed] [Google Scholar]
- 26. Wang J, Lian B, Qi XLet al. Quantized topological magnetoelectric effect of the zero-plateau quantum anomalous Hall state. Phys Rev B 2015; 92: 081107. 10.1103/PhysRevB.92.081107 [DOI] [Google Scholar]
- 27. Wu L, Salehi M, Koirala Net al. Quantized Faraday and Kerr rotation and axion electrodynamics of a 3D topological insulator. Science 2016; 354: 1124–7. 10.1126/science.aaf5541 [DOI] [PubMed] [Google Scholar]
- 28. Mogi M, Kawamura M, Yoshimi Ret al. A magnetic heterostructure of topological insulators as a candidate for an axion insulator. Nat Mater 2017; 16: 516–21. 10.1038/nmat4855 [DOI] [PubMed] [Google Scholar]
- 29. Mogi M, Kawamura M, Tsukazaki Aet al. Tailoring tricolor structure of magnetic topological insulator for robust axion insulator. Sci Adv 2017; 3: eaao1669. 10.1126/sciadv.aao1669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Xiao D, Jiang J, Shin JHet al. Realization of the axion insulator state in quantum anomalous Hall sandwich heterostructures. Phys Rev Lett 2018; 120: 056801. 10.1103/PhysRevLett.120.056801 [DOI] [PubMed] [Google Scholar]
- 31. Allen M, Cui Y, Ma EYet al. Visualization of an axion insulating state at the transition between 2 chiral quantum anomalous Hall states. Proc Natl Acad Sci USA 2019; 116:14511–5. 10.1073/pnas.1818255116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Yu J, Zang J, Liu CX. Magnetic resonance induced pseudoelectric field and giant current response in axion insulators. Phys Rev B 2019; 100: 075303. 10.1103/PhysRevB.100.075303 [DOI] [Google Scholar]
- 33. Liu C, Wang Y, Li Het al. Robust axion insulator and Chern insulator phases in a two-dimensional antiferromagnetic topological insulator. Nat Mater 2020; 19: 522–7. 10.1038/s41563-019-0573-3 [DOI] [PubMed] [Google Scholar]
- 34. Li Y, Liu C, Wang Yet al. Nonlocal transport and one-dimensional conduction in the axion insulator state of MnBi2Te4, arXiv, 2022, preprint: not peer reviewed. https://arxiv.org/abs/2105.10390
- 35. Lin W, Feng Y, Wang Yet al. Direct visualization of edge state in even-layer MnBi2Te4 at zero magnetic field. Nat Commun 2022; 13: 7714. 10.1038/s41467-022-35482-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Fijalkowski KM, Liu N, Hartl Met al. Any axion insulator must be a bulk three-dimensional topological insulator. Phys Rev B 2021; 103: 235111. 10.1103/PhysRevB.103.235111 [DOI] [Google Scholar]
- 37. Song ZD, Lian B, Queiroz Ret al. Delocalization transition of a disordered axion insulator. Phys Rev Lett 2021; 127: 016602. 10.1103/PhysRevLett.127.016602 [DOI] [PubMed] [Google Scholar]
- 38. Li YH, Cheng R. Identifying axion insulator by quantized magnetoelectric effect in antiferromagnetic MnBi2Te4 tunnel junction. Phys Rev Res 2022; 4: L022067. 10.1103/PhysRevResearch.4.L022067 [DOI] [Google Scholar]
- 39. Mogi M, Okamura Y, Kawamura Met al. Experimental signature of the parity anomaly in a semi-magnetic topological insulator. Nat Phys 2022; 18: 390–4. 10.1038/s41567-021-01490-y [DOI] [Google Scholar]
- 40. Zou JY, Fu B, Wang HWet al. Half-quantized Hall effect and power law decay of edge current distribution. Phys Rev B 2022; 105: L201106. 10.1103/PhysRevB.105.L201106 [DOI] [Google Scholar]
- 41. Chen R, Li S, Sun HPet al. Using nonlocal surface transport to identify the axion insulator. Phys Rev B 2021; 103: L241409. 10.1103/PhysRevB.103.L241409 [DOI] [Google Scholar]
- 42. Xu Y, Song Z, Wang Zet al. Higher-order topology of the axion insulator EuIn2As2. Phys Rev Lett 2019; 122: 256402. 10.1103/PhysRevLett.122.256402 [DOI] [PubMed] [Google Scholar]
- 43. Zhang RX, Wu F, Das Sarma S. Möbius insulator and higher-order topology in MnBi2nTe3n + 1. Phys Rev Lett 2020; 124: 136407. 10.1103/PhysRevLett.124.136407 [DOI] [PubMed] [Google Scholar]
- 44. He K, Xue QK. Quantum anomalous Hall heterostructures. Natl Sci Rev 2018; 6: 202–4. 10.1093/nsr/nwy157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Perez-Piskunow PM, Roche S. Hinge spin polarization in magnetic topological insulators revealed by resistance switch. Phys Rev Lett 2021; 126:167701. 10.1103/PhysRevLett.126.167701 [DOI] [PubMed] [Google Scholar]
-
46.
Zhao Y, Liu Q. Routes to realize the axion-insulator phase in
 family. Appl Phys Lett 2021; 119: 060502. 10.1063/5.0059447 [DOI] [Google Scholar]
family. Appl Phys Lett 2021; 119: 060502. 10.1063/5.0059447 [DOI] [Google Scholar] - 47. Lu R, Sun H, Kumar Set al. Half-magnetic topological insulator with magnetization-induced Dirac gap at a selected surface. Phys Rev X 2021; 11: 011039. [Google Scholar]
- 48. Li S, Gong M, Cheng Set al. Dissipationless layertronics in axion insulator MnBi2Te4, arXiv, 2023, preprint: not peer reviewed. https://arxiv.org/abs/2207.09186 [DOI] [PMC free article] [PubMed]
- 49. Goos F, Hänchen H. Ein neuer und fundamentaler versuch zur totalreflexion. Ann Phys 1947; 436: 333–46. 10.1002/andp.19474360704 [DOI] [Google Scholar]
- 50. Kurt Artmann. Calculation of lateral displacement of totally reflected ray. Ann Phys 1948; 437: 87–102. [Google Scholar]
- 51. Renard RH. Total reflection: a new evaluation of the Goos–Hänchen shift. J Opt Soc Am 1964; 54: 1190–7. 10.1364/JOSA.54.001190 [DOI] [Google Scholar]
- 52. Yasumoto K, Oishi Y. A new evaluation of the Goos–Hänchen shift and associated time delay. J Appl Phys 1998; 54: 2170. 10.1063/1.332395 [DOI] [Google Scholar]
- 53. Beenakker CWJ, Sepkhanov RA, Akhmerov ARet al. Quantum Goos-Hänchen effect in graphene. Phys Rev Lett 2009; 102: 146804. 10.1103/PhysRevLett.102.146804 [DOI] [PubMed] [Google Scholar]
- 54. Jiang QD, Jiang H, Liu Het al. Topological Imbert-Fedorov shift in Weyl semimetals. Phys Rev Lett 2015; 115: 156602. 10.1103/PhysRevLett.115.156602 [DOI] [PubMed] [Google Scholar]
- 55. Yang SA, Pan H, Zhang F. Chirality-dependent Hall effect in Weyl semimetals. Phys Rev Lett 2015; 115: 156603. 10.1103/PhysRevLett.115.156603 [DOI] [PubMed] [Google Scholar]
- 56. Shi Lk, Song JCW. Shift vector as the geometric origin of beam shifts. Phys Rev B 2019; 100: 201405. 10.1103/PhysRevB.100.201405 [DOI] [Google Scholar]
- 57. Thouless DJ, Kohmoto M, Nightingale MPet al. Quantized Hall conductance in a two-dimensional periodic potential. Phys Rev Lett 1982; 49: 405–8. 10.1103/PhysRevLett.49.405 [DOI] [Google Scholar]
- 58. Thouless DJ. Quantization of particle transport. Phys Rev B 1983; 27: 6083–7. 10.1103/PhysRevB.27.6083 [DOI] [Google Scholar]
- 59. Niu Q, Thouless DJ. Quantised adiabatic charge transport in the presence of substrate disorder and many-body interaction. J Phys A 1984; 17: 2453–62. 10.1088/0305-4470/17/12/016 [DOI] [Google Scholar]
- 60. Xiao D, Chang MC, Niu Q. Berry phase effects on electronic properties. Rev Mod Phys 2010; 82: 1959–2007. 10.1103/RevModPhys.82.1959 [DOI] [Google Scholar]
- 61. Lensky YD, Song JC, Samutpraphoot Pet al. Topological valley currents in gapped Dirac materials. Phys Rev Lett 2015; 114: 256601. 10.1103/PhysRevLett.114.256601 [DOI] [PubMed] [Google Scholar]
- 62. Liu CX, Qi XL, Zhang Het al. Model Hamiltonian for topological insulators. Phys Rev B 2010; 82: 045122. 10.1103/PhysRevB.82.045122 [DOI] [Google Scholar]
- 63. Zhang H, Liu CX, Qi XLet al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat Phys 2009; 5: 438–42. 10.1038/nphys1270 [DOI] [Google Scholar]
- 64. Zhou H, Li H, Xu DHet al. Transport theory of half-quantized Hall conductance in a semi-magnetic topological insulator. Phys Rev Lett 2022; 129: 096601. [DOI] [PubMed] [Google Scholar]
- 65. Fisher DS, Lee PA. Relation between conductivity and transmission matrix. Phys Rev B 1981; 23: 6851–4. 10.1103/PhysRevB.23.6851 [DOI] [Google Scholar]
- 66. MacKinnon A. The calculation of transport properties and density of states of disordered solids. Z. Physik B 1985; 59: 385–90. 10.1007/BF01328846 [DOI] [Google Scholar]
- 67. Metalidis G, Bruno P. Green’s function technique for studying electron flow in two-dimensional mesoscopic samples. Phys Rev B 2005; 72: 235304. 10.1103/PhysRevB.72.235304 [DOI] [Google Scholar]
- 68. Haug H, Antti-Pekka J. Quantum Kinetics in Transport and Optics of Semiconductors. Berlin: Springer, 2008. [Google Scholar]
- 69. Jiang H, Wang L, Sun QFet al. Numerical study of the topological Anderson insulator in HgTe/CdTe quantum wells. Phys Rev B 2009; 80: 165316. 10.1103/PhysRevB.80.165316 [DOI] [Google Scholar]
- 70. Sitte M, Rosch A, Altman Eet al. Topological insulators in magnetic fields: quantum Hall effect and edge channels with a nonquantized θ term. Phys Rev Lett 2012; 108: 126807. 10.1103/PhysRevLett.108.126807 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.





