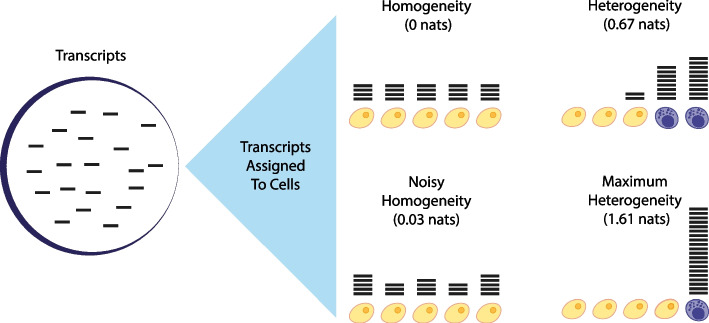
Fig. 1.

An information-theoretic view of sc-Seq data. Transcripts, or more generally counts, of a given gene (shown here as horizontal bars) are assigned to cells after sequencing. If the cell population is homogeneous with respect to the expression of g, then the heterogeneity I(g) will be zero (top left population, $I(g)=0$). In practice, the transcript assignment process is stochastic, and so there will always be some deviation from this ideal (bottom left population, I(g) small). (Note that the technical effects of this stochasticity on the information obtained may be reduced by using a shrinkage estimator to determine the distribution of transcripts (see “Methods” Section)). If the population is heterogeneous, then transcripts may be preferentially expressed in a subset of cells and the information obtained from the experiment, as measured by I(g) will be larger (top right population, I(g) large), reaching a maximum at $log(N)$, where N is the number of cells sequenced, when only one cell expresses the gene (bottom right population, $I(g)=ln(5)\approx 1.61$ largest).Note that the population heterogeneity I(g) is independent of any decomposition of the cell populations into subpopulations (shown here as yellow and purple cells, for illustration). However, given any grouping of the cells into subpopulations, I(g) can be formally decomposed as the sum of the heterogeneity explained by within and in-between subpopulations (see “Results” Section and Fig. 3). This decomposition, but not the overall value of I(g), does depend on the chosen assignment of cells to subpopulations