Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2023 Aug 22;13:13641. doi: 10.1038/s41598-023-40847-6

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2023

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

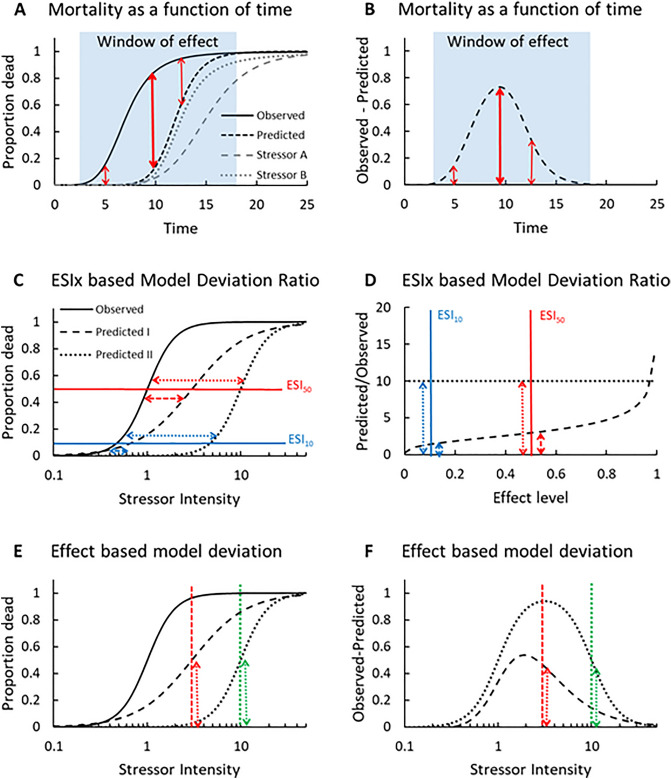
PMC Copyright notice

The mortality as a function of time of two individual stressors, their combination and the prediction using the Multiplicative model (A), and the difference between observed and predicted mortality as a function of time (B). Vertical arrows show the difference between the observed and predicted mortality at selected time points (thick arrow is the time-point of maximal difference). The blue area shows the time interval with differences between observed and predicted effects. Quantifying interactions using Concentration Addition as a null model and the ratio between predicted and observed effects (the model deviation ratio) at specific stressor intensities (ESI_x) (C,D). (C) Observed mortality as a function of cumulated stressor intensity of a stressor combination together with two hypothetical predictions: one where the predicted curve is parallel to the observed curve (dotted curve) and one where the predicted curve has a lower slope than the observed curve (broken curve). Blue and red horizontal lines indicate the difference between observed and predicted curves at the two effect levels ESI₁₀ and ESI₅₀. The ratio between predicted and observed effects as a function of effect level (D), showing that the ratio between the two parallel curves is independent of effect level (dotted line), whereas it varies for non-parallel curves (broken line). For non-parallel curves, the median model deviation ratio is at ESI₅₀. The two effect levels ESI₁₀ and ESI₅₀ from (C) are given in blue and red vertical lines, respectively, in (D). Quantifying interactions using Multiplicative as a null model at different stressor intensities (E,F). (E) Equivalent to (C), but when using IA as a null model the difference between observed and predicted curves are measured as the difference in mortality illustrated by the vertical red and green line crossing the ESI₅₀ of the two predictions. (F) The difference between observed and predicted mortality (varying between 0 and 1) as a function of stressor intensity and illustrates that the difference between observed and predicted mortality is extremely dependent on the chosen stressor intensity.