Toward practical causal epidemiology

Abstract

Population attributable fraction (PAF), probability of causation, burden of disease, and related quantities derived from relative risk ratios are widely used in applied epidemiology and health risk analysis to quantify the extent to which reducing or eliminating exposures would reduce disease risks. This causal interpretation conflates association with causation. It has sometimes led to demonstrably mistaken predictions and ineffective risk management recommendations. Causal artificial intelligence (CAI) methods developed at the intersection of many scientific disciplines over the past century instead use quantitative high-level descriptions of networks of causal mechanisms (typically represented by conditional probability tables or structural equations) to predict the effects caused by interventions. We summarize these developments and discuss how CAI methods can be applied to realistically imperfect data and knowledge – e.g., with unobserved (latent) variables, missing data, measurement errors, interindividual heterogeneity in exposure-response functions, and model uncertainty. We recommend that CAI methods can help to improve the conceptual foundations and practical value of epidemiological calculations by replacing association-based attributions of risk to exposures or other risk factors with causal predictions of the changes in health effects caused by interventions.

Introduction: the need for better causal methods in applied epidemiology

Applied epidemiology seeks to understand preventable causes of diseases and other adverse outcomes in populations, as well as their incidence and prevalence rates. However, at present, the field's core methods and concepts focus on statistical associations, with causal interpretations often assigned using untestable assumptions. For example, relative risk ratios and quantities derived from them, as presented in standard textbooks and applied in countless articles population attributable fractions (PAFs) [35] and population attributable risks (PARs), burdens of disease (BODs), etiological fractions (EFs), probabilities of causation (PCs), and other promisingly named quantities are all based on associations (specifically, relative risk ratios). None of them provides data-driven methods for decisively justifying or refuting causal interpretations. The well-known Bradford Hill considerations and more recent weight-of-evidence (WoE) frameworks for supporting judgments about whether associations should be interpreted causally do not close the logical gap between association and causation [42]. More is needed to create criteria that incorporate both traditional and more recent approaches to causal inference from observational data [15,53,61].

Decades of experience have shown that the practical consequences of the logical gap between data and methods addressing associations, on the one hand, and policy-relevant causal interpretations and recommendations, on the other, can be striking, as illustrated by the following examples:

• •An overwhelming statistical association between higher observed levels of the vitamins beta carotene and retinol and lower observed levels of lung cancer risk at the individual level in large, well-conducted epidemiological studies inspired an intervention (the CARET trial study) to increase levels of these vitamins in people at high risk of lung cancer due to smoking or asbestos. This intervention was followed by a prompt and significant increase in lung cancer risk instead of reducing it, leading to early cessation of the trial [21]. This unanticipated outcome vividly illustrates the distinction between epidemiological concepts of causation (e.g., attributable risk, burden of disease, probability of causation, and so forth) based on associations, and the type of causation that is most relevant for risk managers and policymakers: interventional (or manipulative) causation [14,42]. Interventional causation describes how outcome probabilities change in response to changes in input conditions – e.g., in this example, how lung cancer risk is changed by increased vitamin consumption. The unexpected results of the trial illustrate that the signs and magnitudes of such changes in probabilities of adverse outcomes may have no relation to the signs and magnitudes of observed differences in outcome prevalence or incidence between differently exposed groups. It is common practice in much current applied epidemiology to refer to changes in risk in a target population of interest per unit change in exposure when what is really meant is an observed difference in risk across populations with different exposure levels per unit difference in exposure [14]. These utterly distinct concepts should not be conflated [42].
• •In 2005, the United States Food and Drug Administration (FDA) withdrew approval for use of enrofloxacin, a fluoroquinolone (FQ) antibiotic used to prevent and treat fatal bacterial diseases in poultry, in order to reduce the potential for FQ-resistant bacterial infections in human patients [63]. The decision was supported by an epidemiological risk model that assumed that human cases of FQ-resistant Campylobacter jejuni infection per year are proportional to FQ use in chickens [6]. After more than a decade, however, it has proved difficult to find any impact of agricultural use of these antibiotics on their efficacy in treating human infections [60,66]. As predicted by risk assessment models that examined the likely causes of resistant cases in human patients (primarily, human use of ciprofloxacin) [46], the withdrawal of FQ use in animals was followed by a prompt reversal of a decades-long trend of decreasing Campylobacter jejuni rates [70], and by sustained increases in FQ-resistance in human patients [1,25]. These developments highlight the fallacy of confusing a fraction of human resistant infections attributed to animal use with the fraction of such cases preventable by eliminating animal use.
• •Green et al. [22] conducted a case-control analysis in a large UK data set (the UK General Practice Research Database cohort of about 6 million people) to investigate whether oral bisphosphonates taken to combat osteoporosis increase the risk of esophageal cancer. They reported that the incidence of esophageal cancer was significantly increased in people with one or more previous prescriptions for oral bisphosphonates compared with those with no such prescriptions. But Cardwell et al. [8], examining the same dataset using cohort analysis, reported that the use of oral bisphosphonates was not significantly associated with increased risk of gastric cancer. These opposite conclusions from the same data illustrate the dominant role that modeling assumptions and methods can play in conclusions about associations.
• •Decades of epidemiological studies have shown clear statistical associations between estimated levels of particulate air pollution and observed mortality rates, at least when common confounders are not fully controlled [7], creating a widespread expectation and narrative that reducing particulate air pollution reduces mortality rates (e.g., [27]). Yet, a recent systematic examination of over three dozen intervention studies that reduced ambient air pollution concluded that “[I]t was difficult to derive overall conclusions regarding the effectiveness of interventions” in improving air quality or health [7]. For example, regulatory interventions reduced particulate air pollution in Ireland by about 70%, or over 36 mg/m³, yet produced no detectable reductions in all-cause mortality rates in large affected populations [17,69] despite decades of much-publicized (and ongoing) claims to the contrary [10,27].

These cases illustrate that, in current practice, epidemiological associations and models, and quantitative attributions of risk to exposure based on them, are not always trustworthy guides to how to improve human health. Proposed remedies and improvements such as quantitative bias analysis [29] are often not applied in practice. A more trustworthy type of analysis is needed to identify interventions that demonstrably improve public health.

An area of causal artificial intelligence (CAI) has developed at the intersection of epidemiology [61], philosophy [33], computer science [19], statistics [34,42], econometrics ([23,54, 71], information physics [72], artificial intelligence [5,18,38,39], machine learning [37], systems biology [28], and genetics [20,65]. CAI provides ways to use realistically limited and imperfect observational data, together with mechanistic knowledge, to address interventional causal questions. CAI methods can predict whether and by how much changing exposures would change probabilities of adverse health responses while accounting for differences in conditions and covariates across studies and affected populations. They work only under certain conditions and assumptions, but these can be empirically tested and verified, unlike approaches to causal inference that rely on untestable assumptions [57]. The following sections summarize essential ideas and recent advances in CAI and assess their potential to provide useful answers to causal questions about epidemiological exposure-response data – especially, what fraction of disease cases would be prevented by reducing or eliminating exposure. They seek to provide an alternative to association-based measures such as PAF, PC, etc. to better represent the implications of causal mechanisms – even if only partly elucidated – for understanding and predicting how changing exposure changes risks of adverse health effects.

CAI conceptual framework: qualitative structure of causal networks of probabilistic causal mechanisms

This section introduces an approach to interventional causal analysis and interpretation of data. Although we call it causal artificial intelligence (CAI), this approach was developed by scientists from many disciplines over the past century; Table 1 notes some key milestones in this development. CAI treats causation as predictable propagation of changes (or their probabilities) through networks of random variables. It is not restricted to binary events or to deterministic propagation of changes. Rather, beginning with path analysis [65] and extending through current methods, CAI models causality in terms of propagation of changes through networks of directed dependencies between random variables.

Table 1.

Selected milestones in the development of modern causal analysis.

Milestone	Key Ideas
Path analysis (Wright, 1921) [65]	Variations in effects around their mean values depend on variations in their direct causes.
Counterfactual causation, potential outcomes (Neyman, 1928 [73]; Rubin, 2005 [57])	Differences in causes make their effects different from what they otherwise would have been.
Interventional causation in simultaneous equation models (Haavelmo, 1943 [23])	Exogenously fixing some variables at specified values changes probability distributions of variables that depend on them. Conditioning differs from fixing values [44].
Causal ordering of variables in simultaneous structural equation models (SEMs) (Simon, 1953, 1954 [54,55])	Causes are exogenous to their direct effects. Changes in causes create changes in their direct effects to restore equilibrium.
Predictive causation (Granger causation) in linear time series Wiener, 1956 [74], Granger, 1969 [71]	Past and present changes in causes help to explain and predict future changes in their effects. The future of an effect is not conditionally independent of the past of its causes, given its own past.
Causal loop diagrams (Maruyama, 1963 75])	Dynamic systems adjust until they reach equilibrium. The equilibrium is caused and explained by a balance of the mechanisms that act to change it [38].
Quasi-experiments. Internal and external validity of causal conclusions (Campbell and Stanley, 1963 [76])	Differences in effects are explained by differences in causes and are not fully explained by differences in other factors.
Causal discovery algorithms (Glymour and Scheines, 1986; Glymour et al., 2019 [19, 20])	Conditional independence and dependence relationships in data constrain the set of possible causal models for the data-generating process.
Interventional causation and causal ordering (Simon and Iwasaki, 1988 [56])	Exogenously changing causes changes the probability distributions of their direct effects.
Causal Bayesian networks, structural causal models, nonparametric SEMs, and conditional independence and dependence (Pearl, 2000 [41])	Effects are not conditionally independent of their direct causes, given the values of other variables. Conditioning on common effects induces dependence between parents that are conditionally independent.
Transfer entropy [72] and directed information	Information flows from direct causes to their effects over time. Transfer entropy generalizes Granger causation.
Functional causal models (Shimuzu et al., 2006 [58])	An effect is often a simple (e.g., additive) function of its direct causes and random noise.
Transportability (Lee and Honovar, 2013; Bareinboim and Pearl, 2013 [30, 5])	Invariance of causal mechanisms (represented by CPTs) enables generalization of causal findings across studies.
Invariant causal prediction (ICP) (Peters et al., 2016; Prosperi et al., 2020 [45, 47])	Causal laws are universal: if levels for all of the direct causes of an effect are the same, then the conditional probability distribution of the effect should be the same across settings (e.g., studies) and interventions.

Qualitatively, dependencies can be represented by networks. One way to do so is as follows.

• •Nodes in a network represent random variables.
• •A link between two nodes represents a statistical dependency between them, meaning that observing one provides information about the other, although the dependency need not be causal. (By Bayes' Rule or the definition of conditional probability, statistical dependence is symmetric: if P(X | Y) differs from P(X), then P(Y | X) differs from P(Y), since P(Y | X) = P(X | Y)P(Y)/P(X) and P(X | Y)/P(X) differs from 1. In information-theoretic terms, two random variables X and Y are dependent if and only if they have positive mutual information, I(X; Y) > 0, where the mutual information I(X; Y) measures the expected reduction in uncertainty (entropy) of either variable from conditioning on the other: I(X; Y) = H(Y) - H(Y | X) = H(X) - H(X| Y), where H(X) = entropy of X [11].)
• •Absence of a link between nodes shows that they are conditionally independent of each other, given the values of other variables. For example, in the directed acyclic graph (DAG) model X → Y → Z, where X = exposure, Y = internal dose, and Z = probability of death, Z might be unconditionally dependent on both X and Y (each variable is positively correlated with the other two), but the DAG structure shows that Z is conditionally independent of X given Y: once Y is known, X provides no further information about Z. In this case, Z depends directly on Y but only indirectly on X. Quantitatively, in any such chain model X → Y → Z, observing X gives at least as much information about its direct effect Y as about its indirect effect Z: I(X; Y) ≥ I(X; Z) [11].

• •Directed links (represented by arrows) without causal interpretations simply show one way (typically there are many) to factor a joint distribution of the variables into products of conditional and marginal distributions. For example, the joint distribution for two random variables X and Y can be factored equally well as P(x, y) = P(x)P(y | x), corresponding to the DAG X → Y; or as P(x, y) = P(y)P(x | y), corresponding to the DAG Y → X.
• •Directed links with causal interpretations show the direction of causality: changes propagate from the variable at the tail of an arrow to the variable at its head a concept sometimes formalized via the closely interrelated concepts of directed information flow, transfer entropy, and Granger causation in which information flows from one time series variable X to another Y creates positive mutual information between the past of X and the future of Y, even after conditioning on the past of Y [72, 77]. In a DAG model, if a directed link X → Y has a manipulative (interventional) causal interpretation, then changing the value (or distribution) of X changes the conditional distribution of Y via the formula P(y) = Σ_xP(y | x)P(x). If changes propagate from X to Y and not from Y to X, then only X → Y has a valid causal interpretation as well as a valid statistical interpretation.
• •Undirected links can be used to represent statistical associations without clear directions or causal interpretations, creating graphs that generalize DAGs. For example, if small cities are much more common in the south than in the north of a country, then conditioning on the observation that someone lives in a small city may increase the conditional probability that she lives in the southern region, and yet we might not want to say that either condition is a direct cause of the other.
• •A Bayesian network (BN) is a DAG model in which all links are directed. If the directed links all have causal interpretations, then the BN is called a causal Bayesian network. If each node has a known conditional probability table (CPT), then the BN model is said to be fully specified.

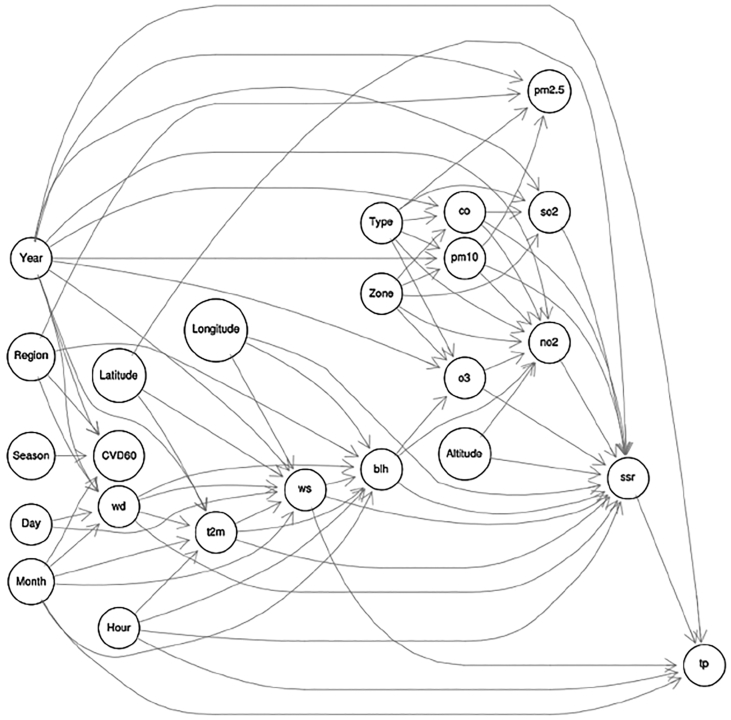
Fig. 1 shows an example of a BN fit to data on air pollution, weather, geographic, and elderly cardiovascular-pulmonary disease (CVD60) mortality variables [64]. The data set contains nearly 50 million records from the United Kingdom, and has adequate power to quantify dozens of direct effects, corresponding to the arrows in Fig. 1. The DAG structure shows that Month is a common ancestor of ozone (o3) and mortality risk (CVD60) and that Region and Year are common parents of fine particulate matter (pm2.5) and mortality risk. If this BN structure is correct, then the many reported associations between these pollutants and mortality risk in studies that do not control for confounders (or common ancestors) such as Month, Region, and Year in Fig. 1 require care in causal interpretation. For example, the famous Harvard Six Cities study [78] concluded that “Although the effects of other, unmeasured risk factors cannot be excluded with certainty, these results suggest that fine-particulate air pollution, or a more complex pollution mixture associated with fine particulate matter, contributes to excess mortality in certain U.S. cities.” A more cautious interpretation would be that the association does not suggest conclusions about what contributes to mortality risk, but shows a need to control carefully for differences among cities in confounders (analogous to Region, Month, and Year in Fig. 1) to discover whether mortality risk depends directly on fine particulate air pollution, or whether, as in Fig. 1, the association between them is explained by confounding.

Fig. 1.

A Bayesian network (BN) structure for air pollutants (pm2.5 = fine particulate matter, pm10 = coarse particulate matter, o3 = ozone, so2 = sulfur dioxide, no2 = nitrogen dioxide, co = carbon monoxide); cardiovascular-pulmonary disease mortality for people over age 60 (CVD60); and related weather and geographic variables (e.g., wd = wind direction, t2m = 2 m temperature, ws = wind speed, etc.). Source: [64].

Quantitatively, conditional probability tables (CPTs) describe dependencies among random variables. A CPT for a node (variable) tabulates the conditional probability of each of its possible values for each combination of values of its parents, i.e., of the variables that point into it (its direct causes, if all arrows have causal interpretations). In notation, denoting the set of parents of X by Pa(X), its CPT is just the set of conditional probabilities P(x | Pa(X)) for each possible value x of X and each possible set of values for Pa(X). For computational practicality, if there are too many possible combinations of parent values to tabulate conveniently, or if some of its parents are continuous, then the multivariate function P(x | Pa(X)) for node X can be approximated by a classification and regression tree (CART) or other function approximation methods popular in machine learning, such as random forest ensembles, deep learning networks, support vector or gradient boosted machines, and so forth. We refer to such conditional probability models generically as CPTs, although they need not be tables. For an input node one with only outward-pointing arrows, i.e., no parents the CPT is simply a marginal probability distribution table, P(x), giving the unconditional probability of each possible value of the variable.

CPTs can be recoded as systems of nonparametric structural equations ([18, 43]). In a causal model, each such equation models a causal mechanism by specifying how the probability distribution for the dependent variable on its left side depends on the values of the independent variables on its right side, which correspond to the dependent variable's parents in a graphical representation. The asymmetry of causality is captured by the convention that changes flow from the right side to the left side: if a right-side variable is changed, then the left-side variable adjusts to a new value to restore equality. As a simple deterministic example, the structural equation. P = nRT/V implies that if an exogenous intervention doubles V, then P will be reduced to half its initial value. The detailed timing of the adjustment process is left unspecified: interventions that change the right-side variables cause the left-side variable to change until the equation is again satisfied, but how long this takes and, more generally, the time frame(s) over which changes are considered is not given by the structural equation (or the corresponding CPT). Dynamic BNs (DBNs) that treat variables in different periods as different variables can model change over time to a limited extent, but different tools, such as systems of algebraic and ordinary differential equations, are needed to simulate dynamic systems in more detail. A system of simultaneous structural equations is called a structural equation model (SEM). An example of a deterministic SEM is the following system of simultaneous equations:

P = nRT/V.

F = PA.

a = F/m.

(For a physical interpretation, variables P, V, T, F, A, m, and a might respectively represent pressure, volume, temperature, force, area, mass, and acceleration in a system involving a piston pushing a load, and n and R are constants.) A corresponding DAG model is as follows, where we subsume constants n and R into the formula (structural equation) determining P from V and T:

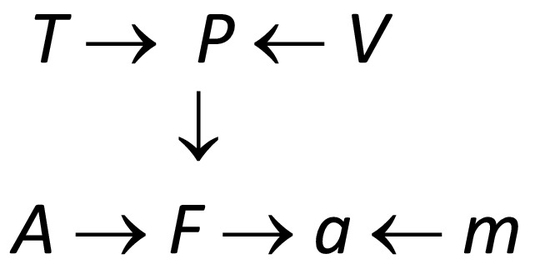
Equations in an SEM corresponding to a causal DAG model can be partially ordered by causality using the principle that effects are determined by their causes [18]. In this DAG, T is shown as a direct cause of P and an indirect cause of F and a, implying that exogenously changing T will change P, which in turn will change F and a (other things, such as V, A and m, being held equal). But exogenously changing F (e.g., by pushing on the piston head) will not change P or T, if this DAG structure correctly describes the system. In a probabilistic SEM, the right sides of structural equations may contain random and latent (unmeasured) variables, so that observed values of right-side variables only determine the probability distributions of left-side variables. Such probabilistic SEMs are equivalent to BNs, with the structural equations playing the roles of CPTs [18]. The equations represent causal mechanisms by describing how probability distributions for the dependent variables on the left respond to changes in their direct causes on the right.

Practical algorithms for quantitative causal inference and prediction with realistically imperfect data

This section summarizes major developments in practical algorithms for quantitative probabilistic inference using BNs and more general probabilistic models. The following classes of algorithms draw useful quantitative conclusions and recommendations from fully specified BNs and observations.

• •Inference algorithms implement Bayes' Rule for fully specified BNs [48]. They compute the posterior distributions of all unobserved variables in a BN (and their joint posterior distribution) given any feasible set of observed or assumed values of other variables. These algorithms are useful for probabilistic expert systems and fault diagnosis, predictive maintenance, medical diagnosis and prognosis, and similar applications where probabilistic inferences are needed about unobserved variables from observed ones.
• •Interventional causal prediction algorithms [32] predict how interventions that set one or more variables to specified values will change the probability distributions of other variables that depend on them. Pioneered in the 1940s in econometrics [23], interventional causation has been further developed in the influential do-calculus of Pearl and co-workers. The do-calculus denotes by do(x) the operation of intervening to set variable X to a specific value, x e.g., setting exposure to zero, or to a reduced value. It determines which interventional causal effects can be estimated from observational data in a BN, and provides constructive algorithms to estimate them, essentially by “surgery” on DAGs that disconnects exogenously manipulated variables from their up-stream causes while allowing their exogenously set values to affect variables that depend on them via CPTs [59].
• •BN learning and causal discovery algorithms [20] use (a) conditional independence and dependence constraints identified in the data, together with (b) scoring methods (similar to traditional model-selection methods such as the Bayesian information criterion (BIC) scores based on the likelihood of the data penalized for model complexity) and (c) knowledge-based constraints (e.g., that high temperature might cause elderly mortality, but elderly mortality cannot cause high temperature) to identify BN structures and CPT estimates that are most consistent with available knowledge and data. These “BN learning” algorithms address the practical question of how to estimate fully specified BNs from data. If arrow directions reflecting causality cannot be uniquely determined from available knowledge and data, then ensembles of multiple plausible BN models can still be used to support quantitative inferences despite model uncertainty [31,34].
• •Causal effect estimation algorithms [62] analyze the DAG structures of BNs to automatically identify subsets of variables to condition on, called adjustment sets, to obtain unbiased estimates of the direct or total causal effect of one variable (such as exposure) on another (such as mortality rate), taking into account the values of other variables (e.g., co-exposures, co-morbidities, or other covariates that also affect mortality risk). These algorithms generalize the idea that it is necessary to condition on common parents or ancestors of exposure and response to control for confounding, but it is necessary to not condition on common children or descendants in order to avoid inducing collider bias. Large BNs often have several possible adjustment sets for the same causal effect. These can be used to check the internal consistency of the BN structure by testing whether the different adjustments sets lead to estimates for causal effects that do not differ significantly from each other [2]. Visualizations of how one variable (e.g., mortality risk) depends on another (e.g., exposure) while conditioning on observed levels of variables in an adjustment set and averaging over the empirical conditional distributions of the remaining variables can be obtained via accumulated local effects (ALE) plots [3].
• •Explanation algorithms. BN inference algorithms can be modified to identify the most probable values of unobserved variables, given observed or assumed values of other variables. These and closely related concepts (most probable explanations, most relevant explanations, and maximum a posteriori probability explanations) can be applied to causal Bayesian networks both to help diagnose and explain observed conditions and to identify how hypothesized future conditions (e.g., failures of complex systems or attaining desired target states) might be caused, prevented, or delayed by current interventions [67].
• •Decision optimization and probabilistic planning algorithms. BN inference algorithms can be modified to solve for values of decision variables to maximize the expected utility of consequences in BNs augmented with decision variables and value nodes, called influence diagrams [51,52]. Multiperiod decision optimization algorithms also allow for planning and decision optimization over time under probabilistic uncertainty [24]. These developments can help manage uncertain risks over time in settings where it is necessary to learn from experience how effective interventions are (e.g., how well mask mandates or vaccines reduce risk of COVID-19 spread), or in which their effectiveness changes randomly over time.

These algorithms are now widely available, e.g., as free R packages in the CRAN repository, https://cran.r-project.org/. They provide computationally practical methods and software for applying fully specified BNs to draw inferences from observations, predict the effects of interventions, and optimize sequences of interventions. Each class of algorithms has also been extended beyond the DAG framework, as simultaneous equations or underlying dynamic models (e.g., ordinary differential equations) with directed cycles in dependency relationships among variables are often more natural models than DAGs for representing systems with simultaneous causation, feedback, or undirected statistical associations [20,23,38].

Fully specified BNs and more general probabilistic models provide constructive solutions to several important technical statistical challenges in applied epidemiology and health risk assessment with realistically imperfect data and knowledge, as follows.

• •
  Unmeasured (latent) variables. BN inference algorithms enable the calculation of joint posterior probabilities for unobserved (latent) quantities by conditioning on the values of observed quantities. Latent variables pose no substantial challenge for inference in a completely specified BN, since BN algorithms automatically calculate their contributions to observations. For example, if X → Y → Z, where X = exposure, Y = internal dose, and Z = mortality risk, and if Y is not measured but X is, then the conditional probability distribution for Z based on the observed exposure X = x is simply P(z | x) = Σ_yP(z | y)P(y | x). This sum models the unobserved contribution of Y by weighing each of its possible values by its conditional probability given observations (“marginalizing out” the unobserved variable). By contrast, if Y is observed to have value y*, then the probability distribution for Z becomes P(z | y*), and the observed value of X is irrelevant. If Y is not measured but diagnosis of a co-morbidity (e.g., chronic obstructive pulmonary disease, COPD) caused by Y is available for each subject, indicated by W = 1 for a positive diagnosis and W = 0 otherwise, then the BN would be extended as follows:

  $$\begin{array}{ccccc}\hfill X\hfill & \hfill \to \hfill & \hfill Y\hfill & \hfill \to \hfill & \hfill Z\hfill \\ & & \hfill \downarrow \hfill & & \\ & & \hfill W\hfill & & \end{array}$$

  The probability distribution of mortality risk Z would now be conditioned on both observed variables, X and W. In short, BN inference algorithms condition on whatever observations are available (e.g., X and W in this example) to obtain predictive posterior distributions for all unobserved quantities, including latent variables (such as Y in this example). If a fully specified BN is not known, however, and must be estimated from data, then latent variables can complicate the estimation process. Unique estimates may be achievable only in special cases, such as for linear models with normally distributed errors [9], and ensembles of possible BNs must be used otherwise [31,34].

• •Missing data. Missing data values can be handled in the BN framework by imputing (sampling) their uncertain values from their conditional distributions given observed values. Adaptations of standard missing data techniques such as the expectation-maximization (EM) algorithm have proved effective for BN learning with incomplete data [37,39].
• •Errors in variables. Measurement errors can be treated as a special case of latent variables. For example, suppose that individual exposures are not known, but are estimated by spatial smoothing of measurements at monitoring stations or satellite data for pollutant data, or from job-exposure matrices for occupational exposures. Then instead of the measurement error-free model X → Z, where X = exposure and Z = mortality risk, a BN with measurement error would be M ← X → Z, where M is the estimated or measured exposure and X is the unobserved (latent) true exposure. Given observed values of M, the corresponding conditional probability distributions for X and Z can be quantified by standard BN inference algorithms.
• •Model specification errors. The use of flexible non-parametric methods such as random forest to quantify CPTs minimizes the potential for model specification error, e.g., omitting relevant variables or interaction terms, using incorrect functional forms, or misspecifying error distributions. In regression models, these mistakes can create statistically significant coefficients for variables that have no causal relevance, but that reduce the mean squared prediction error for the dependent variable arising from model specification errors [13]. Nonparametric BN estimation methods avoid these parametric modeling challenges.
• •Model uncertainty. If causal discovery algorithms identify several possible BN models, then uncertainty about which one is correct (or best describes the data-generating process) can also be treated via latent variables by making the identity of that model the latent variable of interest. An exposure-response model with model uncertainty can be represented as X → Z ← D, where X = exposure, Z = mortality risk, and D = indicator of the correct model. Treating D as a latent variable, predictive distributions for Z with model uncertainty are derived by weighing members of the ensemble of possible models by their probabilities: P(z | x) = Σ_dP(z | x, d)P(d) where d indexes possible models and P(d) is the conditional probability of model d given observations. If the number of possible models is very large and/or prior probabilities for models are unknown, then model-averaging techniques that discard relatively low-likelihood models using Bayes factors can be used to improve computational efficiency [31,34].
• •Interindividual heterogeneity. If different individuals in a population have different individual exposure-response functions, e.g., due to phenotypic variations in biochemistry, then no single aggregate exposure-response relationship can adequately represent their heterogeneous responses to an exogenous change in exposures. Observed sources of heterogeneity, such as differences in age, income, smoking, or health status, can be modeled by causal random forests and generalized random forests [4]. Unobserved sources of interindividual heterogeneity can be modeled as a composite latent variable (the individual's “type”), allowing them to be treated as another special case of latent variables. For example,the model X → Z ← H, where X = exposure, Z = mortality risk, and H = individual type (unobserved) leads to P(z | x) = Σ_hP(z | x, h)P(h) where h indexes possible types; these serve as the components of this finite mixture distribution model.
• •Internal validity of causal conclusions. Internal validity addresses whether estimated causal effects in a study correctly describe causation in the study (Campbell and Stanley, 1963 [76]). To establish the internal validity of causal effects estimates, it is necessary to refute rival (non-causal) explanations for the data and to condition on appropriate adjustment sets of other variables. For BNs, causal effect estimation algorithms allow adjustment sets to be computed from BN DAG structures [62]. Comparing causal effect estimates for multiple adjustment sets (if there are several) reveals whether they are internally consistent.
• •External validity of causal predictions. If a causal BN model is learned (i.e., both its structure and its CPTs are estimated) from data for one or more populations, will its causal conclusions and predictions, e.g., about how mortality risk depends on exposure, prove accurate for a different population? This question of external validity of causal conclusions has challenged generations of epidemiologists and risk assessors (Campbell and Stanley, 1963 [76, 50]). It has been solved relatively recently for causal BNs by using the do-calculus to establish necessary and sufficient conditions for “transportability” (i.e., generalization) of causal relationships, modeled by causal CPTs, from one population to another [5,30]. A key idea is that, while statistical CPTs may differ across populations with different compositions of heterogeneous (non-exchangeable) individuals, a causal CPT with all of its direct causes included should be invariant across populations and interventions [45,47]. This invariant causal prediction property (ICP) for causal CPTs [45], formalizing the intuition that fully stated causal laws are universal, can be tested empirically by testing whether responses are conditionally independent of the study or population from which data come, given the values of the variables.
• •Generalization to new conditions. Causal CPTs satisfying the ICP property can be used to predict exposure-response relationships in target populations with conditions different from those for which data have been collected. This is accomplished by applying the ICP CPTs to the joint distribution of conditions in the target population. What is generalized from past experience is the ICP CPTs. Their implications for observable population exposure-response relationships will depend on the joint distribution of conditions that affect responses. For example, if Z is a risk indicator with a value of 1 for someone who is diagnosed with a certain disease before dying and a value of 0 otherwise, and if P(z | Pa(Z)) is the ICP CPT for Z, with exposure being one of the parents of Z, then an exposure-response curve relating exposure to probability of harm by marginalizing out all other parents (i.e., summing or integrating P(z | Pa(Z)) over all their possible joint values weighted by their respective conditional probabilities or probability densities given the observed level of exposure) may be quite different in different populations. Thus, if Z has two parents, X = exposure and A = age, each scaled to run from 0 to 1, where 1 denotes the maximum value in the population, and if for any specific exposure x and age z the risk is given by the CPT model E(Z | Pa(Z) = (x, a)) = P(Z = 1 | Pa(Z) = (x, a)) = xa, then the exposure-response function in a population of young people with a = 0.2 would be E(Z | x) = 0.2x, but the exposure-response function in an elderly population with a = 0.9 would be E(Z | x) = 0.9x. Invariance (ICP) generalizes the Bradford-Hill consideration of “consistency” in exposure-response associations by recognizing that populations with different distributions of covariates (e.g., age) may have different marginal exposure-response curves for the same (invariant) causal CPT. In this example, the invariant CPT model E(Z | Pa(Z) = (x, a)) = xa allows the result E(Z | x) = 0.2x for the first population to be transported to the prediction E(Z | x) = 0.9x for the second population.

These technical developments address the most common challenges for data analysis with realistically incomplete and imperfect data and knowledge. They offer data-driven options for dealing with data and model uncertainties and for testing whether causal conclusions from past studies hold across diverse study conditions and can confidently be generalized to new situations with new combinations of conditions. However, our main interest is in the new light these advances shed on how to better answer the questions traditionally addressed by attributable risk, PAF, PC, and related epidemiological calculations using associational data without causal mechanisms.

Implications of CAI for calculating and interpreting preventable fractions

Seeing is not doing

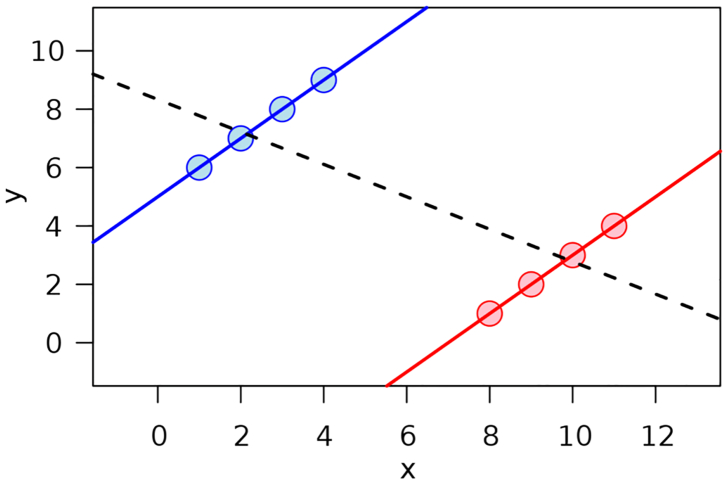
The distinction between inference algorithms and causal prediction algorithms emphasizes a crucial philosophical point: contrary to implicit assumptions commonly made in calculating and interpreting PAF, PC, and other variations on relative risk ratios and absolute risk differences, observational data on exposure and response levels do not provide mechanistic information that may be essential to predict correctly how setting exposure to zero, or to a reduced level, would change responses in a population. Fig. 2 illustrates the problem. It shows 8 data points, one for each of 8 individuals. We interpret x as exposure and y as a health outcome, such as length of life or annual survival probability (scaled to the axes shown). Now, consider an intervention that reduces the value of x for each individual to 0. How will their y values change in response? Standard epidemiological practice uses regression models to estimate the answer, assuming that each dot would slide along an appropriate regression line or curve to a new position with x = 0.

Fig. 2.

Seeing vs. doing. How y values of the individual data points would change if their x values were reduced by a stated amount cannot be determined from the data. Source:https://en.wikipedia.org/wiki/Simpson%27s_paradox

This procedure substitutes the answer to an easy but irrelevant statistical question (what is the y value associated with x = 0 in a regression model fit to the observed data?) for the answer to a hard but relevant causal question: how would reducing x to 0 change each y value? The answer to the latter question is not, even in principle, revealed by the data points alone. Assumptions can be made to help answer it – such as that the observed differences in y values are explained (and caused) solely by differences in corresponding x values, but the validity of resulting predictions and conclusions is then contingent on the validity of the assumptions used in deriving them, which may be uncertain.

Fig. 2 seeks to illustrate this basic distinction between statistical and causal questions [42] by showing data for which it is unclear whether it is more plausible to expect that the dots would slide leftward and downward along their local (upward-sloping, solid) regression lines as x is reduced; or that they would slide leftward and upward along the global (downward, sloping, dashed) line. The more fundamental point is that there is no basis in observed exposure-response data for making either prediction, or some other one (e.g., that the y values of all dots would stay unchanged as x decreases, or that the dots on the right would travel down their local line (red) until x crossed a threshold, perhaps at x = 5, where their y values would jump up to the higher (blue) local line, possibly reflecting that some biological process or resource is no longer saturated or depleted at x values below 5). The responses of y to changes in x simply cannot be predicted correctly with confidence from the data, as the responses depend on causal mechanisms that are not represented in the data. The data show observed levels of x and y, but are silent about the causal mechanisms (e.g., described by CPTs or structural equations) that predict how and whether changing x would change y. As emphasized by Pearl [42] and by econometricians in earlier decades [23,54], seeing is not doing: observational data together with regression equations describing associations among variables do not address causal questions about how taking action to set some variables to new levels will change others. In fairness to current epidemiology practice, it should be noted that observations are often supplemented by assumptions for purposes of causal inference (e.g., assumptions of exchangeability or no hidden confounders), but such assumptions are often untested (and perhaps untestable) or are left implicit, and causal conclusions based on them are too often presented without characterizing the extent to which they depend on uncertain assumptions, as best practice recommends [29].

Ambiguity of counterfactuals for PAFs

The population attributable fraction (PAF) is traditionally defined as the ratio (O - E)/O, where O = observed number of cases and E = expected number of cases under no exposure. The PAF ratio is widely interpreted as an estimate of both (a) the fraction of all cases in a population attributable to exposure; and (b) the fraction of all cases that would not have occurred had there been no exposure (e.g., [35,36]). The CAI framework suggests that these concepts involve crucial ambiguities and that PAF = (O - E)/O has no valid but-for or interventional causal interpretations, as it does not address causal mechanisms. First, the phrase “expected number of cases under no exposure” is ambiguous: it does not distinguish between exposures that are observed to be 0 and exposures that are set to be 0. In general, these give different expected numbers of cases [23,44]. Why exposure is 0 whether because of exogenous interventions or by chance under the conditions that have generated data so far may matter greatly for predicting E. But the (O - E)/O formula does not specify which (if either) is meant.

Second, the expected number of cases with exposure set to any specific level such as 0 depends in general on levels of other covariates that also affect numbers of cases (other parents of risk in a causal BN model), such as age, co-exposures, co-morbidities, region, year, etc. The (O - E)/O formula does not specify how other variables change when exposure is set to 0. It may be physically unrealistic to assume that other variables are left unchanged by an intervention that reduces exposure. For example, reducing one pollutant may change levels of other pollutants (Fig. 1), of weather variables such as precipitation and temperature, of probabilities of comorbidities that in turn affect expected numbers of cases, and so forth. Holding other variables fixed at their pre-intervention values would then be an unrealistic, irrelevant counterfactual scenario. On the other hand, if other variables are set to estimated realistic post-intervention values, then the resulting predicted value of E will reflect not only the direct effect of reduced exposure but also the effects of changes in the values of other parents of E following the change in exposure. To obtain mutually consistent, realistic estimates of how an intervention affects all other variables that affect response it is necessary to engage in CAI causal network modeling or something much like it (e.g., causal simulation modeling). If no explicit decision is made about how to model changes in other (non-exposure) variables caused by an intervention, a common alternative is to use a regression model to estimate E with exposure equals zero. But regression modeling conflates the value of E caused by setting exposure to 0 with the predicted value of E if exposure is observed to be 0 under the pre-intervention conditions that generated the data for the regression model. In addition, the estimated coefficient of exposure in an empirical regression model typically reflects contributions from non-causal factors such as model specification errors, attribution of interaction effects, ignored measurement errors, contributions from correlated variables, and so forth, rather than a purely causal effect of exposure [13]. The value of E predicted by an empirical regression model under the conditions for which data were collected typically has no valid interventional causal interpretation [42] and may not apply for conditions following an intervention that changes exposure levels. CAI methods address this challenge by analyzing the transportability of estimated causal effects to new conditions. Something very similar is needed for any process that uses pre-intervention data to predict post-intervention case numbers, E.

There is not a right or wrong answer to what should be assumed about how other variables change when exposure changes: this is a matter of defining what we mean to calculate. But if E is estimated from a regression model, rather than from a causal model of how variables change in response to an intervention, then it is not clear what the ratio (O - E)/O represents. Contrary to widespread teaching and usage in epidemiology, it is usually clear that it does not represent the fraction of all cases that would not have occurred had exposure been set to zero. To make this methodological point, we consider an extreme case in which each of five pollutants is either present or absent. We denote by 1 the level of a pollutant when present and by 0 its level when absent. Suppose that the causal DAG structure is Z ← X1 → X2 → X3 → X4 → X5 where Z indicates an adverse health response (1 = present, 0 = absent) and X1…X5 indicate the levels of pollutants 1–5. That is, X1 is a direct cause of Z and also of X2; X2 is a direct cause of X3, and so on. Quantitatively, suppose that X1 is currently 1 and that the CPTs specify that, in the absence of exogenous interventions, each variable is 1 if its parent is 1, else it is 0. (Recall that an intervention that exogenously sets a variable equal to a new level disconnects it from its parents.) Under these conditions, considering X5 as the pollutant of interest, a regression model of past observed Z values against corresponding X5 values would yield O = 1, E = 0, and PAF_X5 = 1 as the PAF for pollutant X5. Symmetrically, PAF_X4 = 1, PAF_X3 = 1, and PAF_X2 = 1. What these calculations do not reveal is that setting any of these variables equal to 0 would have no effect on Z: only X1 is a cause of Z. The PAF ratios for the other variables are irrelevant for predicting how or whether Z would change if exogenous interventions set the other exposures to zero. The same applies to probability of causation and burden of disease calculations: PC values of 1 for variables X2 through X5 do not imply that reducing these exposures would have any effect on case numbers.

CAI algorithms make it straightforward to calculate causally meaningful PAFs from a fully specified causal BN model: simply calculate the expected number of cases predicted by the causal BN under present (pre-intervention) and new (post-intervention) conditions. Call the first O and the second E, and apply the PAF = (O - E)/O formula to these values. In the present example, setting X5 to 1 or to 0 leaves Z unchanged, so O = E and the causal PAF for an intervention that changes X5 from 1 to 0 is PAF_X5 = 0. Symmetrically, PAF_X4 = 0, PAF_X3 = 0, and PAF_X2 = 0; but PAF_X1 = 1. Note that PAFs are now not attached to exposures or other risk factors, but to interventions that change levels of exposures (and possibly other variables). That is, instead of attributing some fraction of cases to a pollutant a proposition that makes no testable or falsifiable predictions, and in this sense is devoid of scientific content these intervention-specific causal PAFs predict the fraction of current cases that would be prevented by interventions that change current conditions, thereby altering the data-generating process. Arguably, this is the information that PAFs should provide to have value to policy-makers choosing among various possible interventions. Calculating preventable fractions for interventions also avoids the tendency of PAFs and PCs for risk factors to sum to more than 100% – e.g., the PAFs (and PCs) for pollutants X1 through X5 in the above example to sum to 5. The causal PAF for any (single or combined) intervention is always between 0 and 1.

Discussion and conclusions: toward pragmatic causal PAF calculations

Causal artificial intelligence (CAI) suggests the following perspectives and advice on how to better calculate and interpret epidemiological and health risk assessment concepts such as population attributable fraction (PAF) and similar concepts to be more useful to risk management decision-makers:

• 1.Calculate PAFs for interventions. To inform practical risk management decisions, PAFs should be calculated for interventions rather than for exposures or risk factors. The PAF for an intervention is defined by the familiar formula PAF = (O - E)/O, but with O and E reinterpreted as causal predictions for the relevant incidence rates or risk measures, e.g., expected number of cases per year for population risks or expected cases per person-year for individual risks, without the intervention and with it, respectively. We refer to predicting O, rather than simply recording its observed value, because true incidence rates are seldom perfectly observable, but must be predicted from data with realistic data uncertainties and model uncertainties and limitations (e.g., latent variables, missing data, measurement errors, model specification uncertainty, and interindividual heterogeneity).
• 2.Use causal models to make causal predictions of O and E. Causal predictions of O and E can be obtained from a fully specified causal BN model if one is known. Valid causal predictions of O and E usually cannot be obtained from regression models or other associational models fit to pre-intervention data without modeling relevant causal mechanisms (represented in CAI by causal CPTs or structural causal model equations) [41]. If an appropriate causal model for predicting O and E is not known, then the technical methods and algorithms we have discussed (e.g., ensembles of non-parametric estimates of causal BN structures and CPTs) can be used to estimate uncertainty distributions of O, E, and PAF based on realistically imperfect data and knowledge.
• 3.Interpret resulting PAF estimates, PAF = (O - E)/O, as the preventable fractions of cases for interventions, i.e., (O - E)/O is the fraction of cases that is predicted to be prevented by an intervention that is predicted to replace O with E.

In this view, attributing cases (or of a fraction of cases) to specific exposures, factors or interventions is unnecessary and adds no value to preventable fraction calculations. Attributing cases to causes does not make testable or falsifiable predictions or empirically verifiable or refutable claims. Preventable fraction calculations do. But an intervention that is predicted to reduce population or individual risks (for at least some individuals) may well do so by changing several variables, e.g., levels or conditional probability distributions of multiple pollutants and weather variables that depend on them. The accounting challenge of allocating or attributing credit or blame for results to the multiple changes that jointly produce them may be intellectually interesting, but it does not change anything observable in the world. There is no need or value for such attribution in any rational decision-making process that is driven by changes in observable results, such as the fractional decrease in case incidence caused by an intervention. Likewise, causal determination exercises that seek to determine whether specific exposures should be called causes (or likely causes, possible causes, etc.) of specific health outcomes, are exercises in terminology without empirical content: they are not needed or useful for predicting the consequences of interventions using CAI methods.

From this perspective, what matters for risk management decision-making is how alternative feasible interventions change outcomes (or their probabilities). This cannot in general be answered from associations between observations in past (pre-intervention) data; nor by any other analysis of pre-intervention data that does not model relevant causal mechanisms. But it can be answered straightforwardly by CAI methods that describe relevant mechanistic knowledge via CPTs or structural equations. Making qualitative causal determinations and calculating attributable fractions (and PCs, PARs, BODs, and related differences and ratios) for exposures and other risk factors based on regression models or other associational analyses of pre-intervention data, without predicting post-intervention changes in outcomes or their probability distributions using models of causal mechanisms, should be viewed as purely definitional exercises without empirical content. Students and practitioners can safely skip them without impairing ability to identify decisions that make preferred outcomes more probable. On the other hand, epidemiologists who wish to predict how alternative interventions would affect public or occupational health should use CAI methods to estimate O and predict E from available data and from estimated causal CPTs or nonparametric structural causal models representing high-level summaries of causal mechanisms. These tools allow calculation of preventable fractions and related quantities, such as uncertainty distributions for absolute numbers of cases per year or per person-year, before and after interventions. Ultimately, information about changes in outcome probability distributions caused by interventions, not attribution of fractions of cases to risk factors, is needed to guide more causally effective risk management decision-making that more reliably causes desired results.