Abstract

In this work, we computed electrical conductivities under ambient conditions of aqueous NaCl and KCl solutions by using the Einstein–Helfand equation. Common force fields (charge q = ±1 e) do not reproduce the experimental values of electrical conductivities, viscosities, and diffusion coefficients. Recently, we proposed the idea of using different charges to describe the potential energy surface (PES) and the dipole moment surface (DMS). In this work, we implement this concept. The equilibrium trajectories required to evaluate electrical conductivities (within linear response theory) were obtained by using scaled charges (with the value q = ±0.75 e) to describe the PES. The potential parameters were those of the Madrid-Transport force field, which accurately describe viscosities and diffusion coefficients of these ionic solutions. However, integer charges were used to compute the conductivities (thus describing the DMS). The basic idea is that although the scaled charge describes the ion–water interaction better, the integer charge reflects the value of the charge that is transported due to the electric field. The agreement obtained with experiments is excellent, as for the first time electrical conductivities (and the other transport properties) of NaCl and KCl electrolyte solutions are described with high accuracy for the whole concentration range up to their solubility limit. Finally, we propose an easy way to obtain a rough estimate of the actual electrical conductivity of the potential model under consideration using the approximate Nernst–Einstein equation, which neglects correlations between different ions.
1. Introduction
Electrolyte solutions are ubiquitous in nature, where ions can play a key role in many living organisms.1 Electrolytes are also important in many other fields such as battery technology2−4 and desalination processes.5 Electrolyte solutions have always been the subject of scientific interest1,6−9 and computer simulations can be a valuable tool for the study of complex phenomena related to these electrolyte solutions in combination with experimental studies. In the 1970s, Heizinger, Vogel, Singer, and Sangster10−14 published the first simulation studies of ionic systems. However, the computational cost of the simulations and the lack of suitable force fields for water and electrolytes did not allow major advances until recent years.
Computational simulations are useful tools for studying phenomena elusive to experiments and for predicting properties of interest. Nevertheless, a suitable force field for the studied system is needed. In the case of aqueous electrolyte solutions, force fields for water and ions are necessary.15 In the case of water, the first force field was proposed by Bernal and Fowler in 1933.15 Fifty years later, Jorgensen and co-workers started to develop new potential models, such as the TIP3P,16 the TIP4P,16 and the TIP5P17 force fields. At the same time, the popular SPC/E force field was developed by Berendsen and co-workers.18 Later, in the 2000s, the knowledge gained from the aforementioned models allowed the development of two of the water models that best reproduce a wide range of properties, which are TIP4P-Ew19 and TIP4P/2005.20 In fact, the TIP4P/2005 potential is able to reproduce a variety of properties such as densities, viscosities, and the temperature of the maximum in density (TMD).21−23 There is no classical model able to reproduce all properties of pure water.21,24 One option to improve results of the previous mentioned force fields is to use polarizable models, such as the HBP,25 the MB-Pol,26 or the BK3.27 However, these force fields are between three and ten times more computationally expensive than the nonpolarizable force fields and are also not able to reproduce certain properties simultaneously, such as TMD and melting temperature.24 Besides water models, ion–ion and ion–water interactions have to be described to study electrolyte solutions. It is in the recent years that a large variety of force fields for salts have been proposed.28−61 Among the most popular force fields for ions, we can find the one proposed by Joung and Cheatham42 (JC), which includes all the alkali halides. These can be used in combination with three different water models, namely, TIP3P, TIP4P-Ew, and SPC/E with the JC-SPC/E being the one that provides overall better results. The other popular force field that is widely used in the literature is the one developed by Smith and Dang34 (SD) in combination with SPC/E water.18 Although these force fields have been quite successful in describing many properties of electrolytes (e.g., densities, structure), they fail in describing properties such as solubilities, viscosities and activity coefficients.62
In an attempt to overcome the limitations of current force fields for electrolytes, the idea of using scaled charges for the ions was suggested. The concept of scaled charges (i.e., assign a charge smaller than one for monovalent ions) arises from the work of Leontyev and Stuchebrukhov63−68 who proposed a charge of ±0.75 (in electron units) for ions in solution (this was also denoted as Electronic Continuum Correction, ECC). The use of scaled charges has also been proposed by Kann and Skinner.69 However, in this case, the value of the scaled charge is selected in such a way that the potential of mean force between ions at infinite dilution and large distances should be the same in experiments and in the force field (so that the model recovers the experimental Debye–Huckel law at infinite dilution). As the potential of mean force depends on the dielectric constant of the water model, so does the value of the scaled charge, leading to a value of ±0.85 in the particular case of water when described by the TIP4P/2005 model. The use of scaled charges for ions in solution has undergone a significant expansion in the last years. Different groups have proposed new force fields with scaled charges, including those of Jungwirth and co-workers,70−74 Barbosa and co-workers,75,76 Li and Wang,77 and Bruce and van der Vegt.78 Other authors have proposed the use of different scaled charges for the cation and anion (charging the surrounding water molecules to maintain the electroneutrality of the system).79−83 Breton and Joly also studied the effect of introducing scaled charges for studying interfacial properties.84 In this context, we developed a model for NaCl based on scaled charges.48 Later, we considered a larger number of salts and we proposed the Madrid-2019 force field,58,59 which includes all the possible alkali halides, some divalent salts (Mg2+ and Ca2+), and sulfates (SO42–). We have shown in previous works that this force field is able to reproduce different properties of interest, such as the salting out effect of methane,85 the TMD of different salt solutions,86 the freezing depression of ice in the presence of different electrolytes,87 or different properties of seawater.88 Although scaled charges improve the results in the majority of properties with respect to unit charge models, there is no unique value of the scaled charge that describes all properties correctly. As we have recently shown, the scaled charge can be taken as a fitting parameter depending on the property that one wants to reproduce.61 Transport properties are among the most interesting properties that can be studied by simulation and that traditional force fields of electrolytes have never been able to reproduce correctly.89 In our recent work, we proposed the Madrid-Transport force field,60,61 which uses a scaled charge of q = ±0.75 and that is able to reproduce transport properties, such as the viscosities and diffusion coefficients of water and ions in the whole concentration range. This force field has also been able to reproduce transport properties in the presence of hydrogen.90 It should be mentioned that the introduction of scaled charges improves a number of properties of electrolytes but deteriorates the value of the free energy of solvation (although it can be corrected via theoretical corrections85).
In this work, we want to analyze in detail the quality of the predictions for electrical conductivities of force fields by using either integer or scaled charges. To the best of our knowledge, such a detailed comparison has never been presented before. As we will show in the next section, electrical conductivities can be calculated with the Einstein–Helfand (EH) equation.91−97 In a preliminary but pioneering work, Lyubartsev and Laaksonen98 evaluated the electrical conductivities of NaCl aqueous solutions at different concentrations with the flexible SPC model for water and ions described as charged LJ particles by using the Green–Kubo (GK) equation99 (which is strictly equivalent to the Einstein–Helfand relation). Due to the computational cost of evaluating the conductivities in this way,100 many authors tend to calculate the electrical conductivities by using the Nernst–Einstein equation (i.e., neglecting the ion–ion correlations).101−106 Although this is cheaper from a computational point of view, the results are not exact (as this is an approximation) and overestimate the real conductivities of the model. Electrical conductivities have been accurate and extensively calculated (through GK or EH) by different authors for ionic liquids.91,92,107−110 In the case of aqueous electrolyte solutions, there are a few studies in which the conductivities were properly evaluated.93,111,112 Martí, Guardia, and co-workers111 calculated electrical conductivities of NaCl solutions at different concentrations using the Smith and Dang34 ion force field with SPC/E water18 (SD-SPC/E). Shao et al.112 also calculated the conductivities of NaCl solutions but using in this case the Joung and Cheatham42 force field in combination with SPC/E water (JC-SPC/E). In fact, these authors showed interesting results about the existence of finite size effects when conductivities were calculated with the Nernst–Einstein relation. There are also semiempirical fitted models that try to reproduce the electrical conductivities of NaCl solutions in solvent mixtures, such as water–propylene carbonate113 or water–monoethylene glycol.114 Other authors have also rigorously computed electrical conductivities for molten salts.115,116 Nevertheless, there is no comprehensive molecular dynamics (MD) study of the performance of different force fields of ions and water for reproducing the electrical conductivities of NaCl solutions in water.
The main purpose of this work is to provide a benchmark to calculate electrical conductivities of aqueous electrolyte solutions, to show that there is a force field able to reproduce the experimental conductivities of NaCl and KCl solutions, and finally, from a deeper perspective, we want to demonstrate that to reproduce conductivities the two surfaces present in water have to be simultaneously described. We will properly evaluate the electrical conductivities of different well-known ion force fields in combination with different water force fields. Besides, in this work, we introduce a new “conceptual” strategy to determine electrical conductivities. As we have mentioned in the past, water (and aqueous solutions) has two surfaces: the potential energy surface (PES) that describes the energy of each configuration of the system and the dipole moment surface (DMS) that describe the dipole moment of each configuration.117−119 The key idea is that these two surfaces can be described by different fitting parameters (i.e., with different charges in our case). In this work, we use a force field with scaled charges to perform the MD simulations of aqueous electrolyte solutions. Only the PES is needed to perform these simulations as we are using the linear response theory, which evaluates transport properties (electrical conductivities in this work) by analyzing the fluctuations of the system when at equilibrium (in the absence of an electric field in the case of electrical conductivities). We will use the Madrid-Transport force field (q = ±0.75) for the PES as it is able to describe other properties of electrolyte solutions accurately (i.e., densities, viscosities, and diffusion coefficients). The obtained trajectories are analyzed employing unit charges to calculate the electrical conductivities (as integer charges instead of partial charges provide a better representation of the DMS). In this way, we will show how to evaluate conductivities of aqueous electrolyte solutions with a new methodology that yields reproducibility of the experimental conductivities of NaCl and KCl solutions by using a scaled charge force field.
2. Methodology
Electrical conductivities can be calculated using the Einstein–Helfand relation:91−95
| 1 |
where V is the system volume, kB the Boltzmann constant, T the temperature, r⃗i(t) and r⃗i(0) the position of the ith particle at time t and 0, respectively, and the ⟨[r⃗i(t) – r⃗i(0)]2⟩ term is the mean square displacement (MSD). Taking into account that the dipole moment of the system can be defined as
| 2 |
we can obtain the following equation for the conductivity in function of the mean square dipole displacement of the system:
| 3 |
This way, the conductivity can be easily obtained from the slope of the mean square dipole displacement versus time (in the Supporting Information, we show this plot for different initial seeds of the MD simulations).
| 4 |
Please note that qi is equivalent to e·zi. We define particles between 1 and N/2 as cations and particles between N/2 + 1 and N as anions. Thus, we can define for a 1:1 electrolyte the Onsager coefficients1 (Λij) for the different interactions between cations (+) and anions (−):
| 5 |
| 6 |
| 7 |
| 8 |
where N is the total number of ions. Combining eq 4 with eqs 5–8, the electrical conductivity can be calculated from
| 9 |
Eq 9 is strictly equivalent to eqs 1 and 3. Note that in all these equations, we include only the charge and positions of the ions. We do not consider water (solvent) molecules because it is a neutral molecule that does not contribute to the electrical conductivity.
Since the evaluation of electrical conductivities by the previous methodology can be computationally demanding, some authors use the approximate Nernst–Einstein (NE) equation,120 which relates the electrical conductivity to the self-diffusion coefficients of the ions:
| 10 |
where q is the charge of the ions, ρ is the number density of the salt, and D+ and D– are the self-diffusion coefficients of the cation and anion, respectively. The NE approximation assumes that the only terms that contribute to the conductivities are those of the particle with itself. Note that whereas there are N2 terms in the rigorous expression of the conductivity (eq 4), there are only N terms when using the NE relation (eq 10). The NE relation thus can be obtained from eq 1 by assuming that the displacement of ions is independent (i.e., ⟨ri · rj⟩ = 0 for i ≠ j). Making this assumption, electrical conductivities can be easily obtained for equimolar salts with eq 10. For the evaluation of conductivities with the NE equation, we have calculated the self-diffusion coefficients of both Na+ and Cl– by using the Einstein relation (eq 11):
| 11 |
where r⃗i(t) and r⃗i(0) are the position of the ith particle at time t and 0, and the ⟨[r⃗i(t) – r⃗i(0)]2⟩ term is the MSD. All diffusivities in this work are corrected using the hydrodynamic corrections of Yeh and Hummer,121,122 which are described as
| 12 |
where Di is the diffusion coefficient with the applied corrections of Yeh and Hummer, DiMD is the diffusion coefficient initially obtained by simulations, ξ is a dimensionless constant equal to 2.837, η is the computed viscosity at the studied concentration (which is shown to exhibit no finite size effects121,123,124), and L is the length of the simulation box.
3. Simulation Details
Electrical conductivity is not a property for which there are many previous results, and it is interesting to see whether two groups using different software packages (GROMACS vs LAMMPS), slightly different methodologies (the individual calculation of the Onsager coefficients versus the global expression), and different system sizes yield the same result for a specific model. Since we also aim to use the results of this work as a benchmark for people computing electrical conductivities in the future, and we want to ensure that the good agreement with experiment that is observed here is true regardless of the MD software or postprocessing program used for the computation. As one group is located in Madrid (UCM) and the other in Delft (TU Delft), they will be denoted as Madrid and Delft groups. Concentrations of the salts will be given in molality units, so that a solution with a concentration 1 m corresponds to 1 mol of salt per kilogram of water. All the results of this work correspond to room temperature and atmospheric pressure (i.e., 298.15 K and 1 bar). Note also that error bars of all the results are calculated by both groups as the standard deviation the property obtained in each run using different initial seeds divided by the square root of the number of runs.
3.1. Madrid Group
All MD simulations were performed with GROMACS125,126 (version 4.6.7). The leapfrog integrator algorithm127 with a time step of 2 fs was used. We also employed periodic boundary conditions in all directions. Temperature and pressure were kept constant using the Nosé–Hoover thermostat128,129 and Parrinello–Rahman barostat,130 both with a coupling constant of 2 ps. For electrostatics and van der Waals interactions, the cutoff radii were fixed at 1.0 nm, and long-range corrections in the energy and pressure were applied to the Lennard-Jones part of the potential. The smooth PME method131 was used to account for long-range electrostatic forces. Water geometry was maintained using the LINCS algorithm.132,133 To compute conductivities, we have simulated systems of 4440 water molecules and the corresponding number of ions for the desired concentration (e.g., 80 NaCl molecules for a concentration of 1 m as shown in Tables 1 and 2). We performed an initial NpT simulation of 20 ns to accurately calculate the volume of the system. After that, using the average volume obtained in the NpT simulation, we have carried out five independent runs in the NVT ensemble. Runs of 200 ns were performed for the lowest concentration (i.e., 1 m) and of 120 ns for the higher concentrations (2, 4, and 6 m). Thus, typically around 600 ns (5 × 120) or 1 μs (5 × 200) are needed to compute electrical conductivities of each model and thermodynamic state. The electrical conductivities were obtained from fitting the mean square dipole displacement (eq 2) versus time between 50 and 1000 ps, as shown in eq 3 (in the SI we also provide the results from fitting the data between 50 and 2000 ps).
Table 1. Computed Electrical Conductivities (σ in Units of S·m–1) of Aqueous NaCl Solutions from the EH Relations (Eq 3) for Different Molalities (m in Units of molsalt·kgwater–1) and System Sizesa.
| m | nw | ns | ρ | η | σ | σNE | σNE+YH | |
|---|---|---|---|---|---|---|---|---|
| Expt. | 0 | – | – | 997.043 | 0.89 | 0 | – | – |
| Madrid | 0 | 4440 | 0 | 997.3(3) | 0.85(5) | 0 | 0 | 0 |
| Delft | 0 | 1000 | 0 | 997.9(3) | 0.82(1) | 0 | 0 | 0 |
| Expt | 1 | – | – | 1036.21 | 0.97 | 8.48 | – | – |
| Madrid | 1 | 4440 | 80 | 1035.2(5) | 0.97(7) | 7.8(1) | 9.7(2) | 10.6(2) |
| Delft | 1 | 1000 | 18 | 1034.8(1) | 0.929(9) | 8.7(2) | 9.6(1) | 11.2(1) |
| Delft | 1 | 555 | 10 | 1034.9(1) | 0.93(1) | 8.7(2) | 9.6(2) | 11.5(2) |
| Expt. | 2 | – | – | 1072.27 | 1.08 | 14.49 | – | – |
| Madrid | 2 | 4440 | 160 | 1070.3(5) | 1.12(7) | 14.0(1) | 17.3(1) | 18.9(1) |
| Delft | 2 | 1000 | 36 | 1069.9(2) | 1.07(2) | 14.3(5) | 17.3(2) | 19.9(2) |
| Delft | 2 | 555 | 20 | 1070.1(1) | 1.08(2) | 13.8(6) | 16.7(1) | 19.9(1) |
| Expt. | 4 | – | – | 1136.91 | 1.35 | 22.04 | – | – |
| Madrid | 4 | 4440 | 320 | 1135.4(5) | 1.44(10) | 20.1(4) | 27.3(1) | 29.6(1) |
| Delft | 4 | 1000 | 72 | 1134.92(7) | 1.37(3) | 20.4(8) | 27.4(2) | 31.3(2) |
| Delft | 4 | 555 | 40 | 1135.31(9) | 1.32(3) | 21.6(5) | 26.5(2) | 31.4(1) |
| Expt. | 6 | – | – | 1192.88 | 1.75 | 25.03 | – | – |
| Madrid | 6 | 4440 | 480 | 1194.5(5) | 1.79(10) | 22.2(8) | 32.6(01) | 35.2(01) |
| Delft | 6 | 1000 | 108 | 1194.0(2) | 1.69(2) | 23.8(5) | 32.53(7) | 37.04(8) |
| Delft | 6 | 555 | 60 | 1194.0(1) | 1.69(1) | 23.8(6) | 32.2(3) | 37.7(3) |
All simulations were performed at 1 bar and 298.15 K, using the Madrid-Transport model. The number of water molecules (nW) and NaCl molecules (ns), the corresponding densities (ρ in units of kg m–3) and viscosities (η in units of mPa·s) are shown for all molalities. Additional electrical conductivities computed using the Nernst–Einstein with (σNE+YH in units of S·m–1) and without (σNE in units of S·m–1) Yeh–Hummer finite-size corrections121,122,124 are reported as well. Numbers in parentheses are the uncertainty in the last digit of the results.
Table 2. Computed Electrical Conductivities (σ in Units of S·m–1) of Aqueous KCl Solutions from the EH Relations (Eq 3) for Different Molalities (m in Units of molsalt·kgwater–1) and System Sizesa.
| m | nw | ns | ρ | η | σ | σNE | σNE+YH | |
|---|---|---|---|---|---|---|---|---|
| Expt. | 0 | – | – | 997.043 | 0.89 | 0 | – | – |
| Madrid | 0 | 4440 | 0 | 997.3(3) | 0.85(5) | 0 | 0 | 0 |
| Delft | 0 | 1000 | 0 | 997.9(3) | 0.82(1) | 0 | 0 | 0 |
| Expt. | 2 | – | – | 1081.5 | 0.90 | 19.98 | – | – |
| Madrid | 2 | 4440 | 160 | 1081.1(5) | 0.95(5) | 20.4(9) | 24.0(1) | 25.8(2) |
| Delft | 2 | 1000 | 36 | 1080.6(1) | 0.91(4) | 20.8(3) | 23.7(2) | 26.7(3) |
| Delft | 2 | 555 | 20 | 1080.8(1) | 0.92(2) | 20.8(5) | 22.8(4) | 26.5(3) |
| Expt. | 4 | – | – | 1152.2 | 0.94 | 34.15 | – | – |
| Madrid | 4 | 4440 | 320 | 1152.3(5) | 1.03(7) | 32.5(6) | 40.5(1) | 43.1(1) |
| Delft | 4 | 1000 | 72 | 1151.60(5) | 1.00(2) | 32.9(9) | 39.7(7) | 44.8(7) |
| Delft | 4 | 555 | 40 | 1151.81(3) | 0.99(2) | 32.4(7) | 38.8(2) | 45.1(3) |
All simulations were performed at 1 bar and 298.15 K, using the Madrid-Transport model. The number of water molecules (nW) and KCl molecules (ns), the corresponding densities (ρ in units of kg m–3) and viscosities (η in units of mPa·s) are shown for all molalities. Additional electrical conductivities computed using the Nernst–Einstein with (σNE+YH in units of S·m–1) and without (σNE in units of S·m–1) Yeh–Hummer finite-size corrections121,122,124 are reported as well. Numbers in parentheses are the uncertainty in the last digit of the results.
3.2. Delft Group
MD simulations are carried out on the DelftBlue supercomputer at TU Delft134 with the large-scale atomic/molecular massively parallel simulator (LAMMPS: version August 2018).135 Periodic boundary conditions are imposed in all directions, and the velocity-Verlet algorithm is used with a time step of 2 fs. The Nosé–Hoover thermostat and barostat128−130 are set with coupling constants of 0.1 and 1 ps, respectively. The SHAKE algorithm is used to fix the bond lengths and angles of water.135,136 A cutoff of 1.0 nm is used for both the Lennard-Jones and electrostatic potentials. Long-range electrostatic interactions are modeled using the particle–particle particle–mesh (PPPM) method137,138 with a relative error139 of 10–5. Analytic tail corrections137 are applied to the Lennard-Jones interactions for both energies and pressures. Initial configurations are created using PACKMOL (v20.3.1).140 To compute electrical conductivities, self-diffusivities, and shear viscosities, the OCTP plugin141 is used. In this plugin, the Einstein relations are used in combination with the order-n algorithm137,142 to compute transport properties. All details on the OCTP plugin can be found in ref (141). The approach to evaluate conductivities is based on the computation of the Onsager coefficients (Λij) for the cation–cation, anion–anion, and cation–anion interactions independently as shown in eqs 4–9. These equations are used to compute the exact electrical conductivities, accounting for ion–ion correlations. In the SI we have collected the results for the individual contributions to the electrical conductivities (i.e., σ++,σ+–, σ–+, and σ––) computed from each individual Onsager coefficient. To evaluate the electrical conductivities, the system sizes were 555 or 1000 water molecules (the corresponding number of ion molecules is dictated from the molality of each system), as we have listed in Tables 1 and 2. To accurately compute the average volume of the simulation box, simulations of 20 ns in the NpT ensemble were initially carried out (10 ns equilibration runs followed by 10 ns production runs). The self-diffusivities, viscosities, and Onsager coefficients are calculated from production runs of 200 ns in the NVT ensemble. Three different simulations were carried out with different initial velocities for all molalities to obtain statistics. Thus, a total simulation time of ca. 600 ns is required to compute the electrical conductivities of each model and thermodynamic state.
4. Results
4.1. Electrical Conductivities of Popular Force Fields
In previous studies, we have shown that popular force fields (that use integer charges for the ions) are not able to reproduce transport properties, such as viscosities, diffusion coefficients of water in salt solutions, and self-diffusion coefficients of ions.58,59,61 Here we investigate if these models also fail in accurately predicting another important transport property, namely, the electrical conductivity. In Figure 1, results of the electrical conductivity of NaCl obtained in this work for two popular force fields (i.e., Joung and Cheatham42 and Smith and Dang34) that use integer charges combined with the SPC/E water model are compared to experiments. Contrary to previous studies that only focused on concentrations up to 4 m, in this work, we have evaluated the conductivities in the whole concentration range, i.e., up to the experimental solubility limit of NaCl (6.1 m). Our results at 4 m for the JC-SPC/E are in excellent agreement with those obtained by Shao et al.112 using the Green Kubo formalism. Results presented in Figure 1 were obtained from the Madrid group. It is clear that electrical conductivities are underestimated with respect to experiments by the models using integer values for the charge. The SD-SPC/E is slightly more accurate compared to the JC-SPC/E, but also underestimates the electrical conductivities. Thus, it is evident that these two popular force fields for NaCl are not able to reproduce electrical conductivities. These models overestimate the experimental viscosities of NaCl solutions.61 It is not surprising that electrical conductivities are underestimated, as intuitively one would expect that an overestimate of the viscosity would lead to an underestimate of the diffusion coefficient of the ions and, therefore, to an underestimate of the electrical conductivity.
Figure 1.
Electrical conductivities (computed by the Madrid group) as a function of NaCl concentration obtained with the different models studied in this work using eq 3 at temperature T = 298.15 K, and pressure p = 1 bar. Note that Madrid-2019 PES (red empty squares) uses scaled charges in both MD simulations and for computing the conductivities, but Madrid-2019 PES+DMS uses scaled charges for the dynamics and integer charges for computing the conductivities. Experimental results have been taken from ref (143).
4.2. Electrical Conductivities of Scaled Charge Models
Unit charge force fields cannot reproduce electrical conductivities of aqueous solutions, but in previous works we have demonstrated that scaled charge models significantly improve the description of transport properties as viscosities and self-diffusion coefficients.60,61 Thus, we have now employed the Madrid-2019 force field to observe whether we can improve the results of the unit charge force fields. This force field uses scaled charges for the ions (in particular ±0.85). In Figure 1, we show the results for the conductivities of the Madrid-2019 model (red empty squares). Surprisingly we do not obtain better results than those of the unit charge models. This was also observed by Gullbrekken et al.144 in their recent work in which they studied the electrical conductivities by using an integer charge force field but then when scaling the charges they did not observe differences. Regarding Madrid-2019 results, one may wonder how is it possible than a force field that yields better results for viscosities and diffusion coefficients of aqueous solutions does not perform equally well for electrical conductivity. We provide now a possible explanation for this puzzling behavior. As discussed in detail previously,117 water has two different surfaces, the PES and the DMS. In the absence of an external macroscopic electric field, all properties of a system can be determined in computer simulations from the PES. The DMS surface is not needed to determine any property of a system when an external electric field is not applied. However, certain properties describe the response of a system to an external electric field. In particular, the dielectric constant and electrical conductivity are response functions of this type. Obviously, these properties are relevant only when an external electric field is applied to the system. Therefore, to determine these response functions in computer simulations, it is required to describe both the PES and the DMS. A clarification is now in order. The PES simply gives the energy of a system provided the positions of all of the nuclei of the system. The PES only depends on the position of the atoms and does not depend on any macroscopic property such as the viscosity or the dielectric constant. Sometimes it is stated that the dielectric constant enters into the description of the PES in the case of electrolytes. This is not correct. Even for electrolytes, one simply needs to know the position of the atoms to determine the energy of the system, and the value of the dielectric constant is not needed. The origin of this confusion arises from the fact that at infinite dilution, and when r tend to ∞, the potential of mean force w(r) between two ions obtained defined from the radial distribution function g(r) using the following expression:
| 13 |
can be obtained from the knowledge of the dielectric constant ϵr as follows:
| 14 |
However, the potential of mean force is not the PES, and besides this expression is valid only in the Debye–Huckel limit (i.e., at infinite dilution of electrolyte and infinitely large distances). The summary is that the dielectric constant does not enter in the description of the PES, and in the absence of an external electric field, all properties of an aqueous electrolyte solution can be obtained from the PES and the knowledge of the DMS is not needed.
Imagine that a model can describe correctly the viscosities and the diffusion coefficients. This is an indicator that the PES is described correctly. Imagine now that the electrical conductivity is not well described. How can we solve this paradox? The answer is rather simple: the PES is well described, but the DMS is not well described. Often partial charges are used to describe the PES and these charges are also used to describe the DMS. We have suggested sometime ago that the charges that are good to describe the PES may not be suitable to describe the DMS.117 We have provided some indications by analyzing the behavior of the dielectric constant of water. Jorge and co-workers119,145 have shown that the same is true for the dielectric constant of alcohols, and Bowman and co-workers followed up on this idea.146,147
Here, we use different charges to describe the PES and the DMS of electrolytes in water. In particular, we shall use scaled charges for the ions in water for the PES while we shall use nonscaled charges (i.e., integer charges) to describe the DMS. The way to implement this idea is rather simple. Since we are using linear response theory (so that the electrical conductivity is computed by simulating the system in the absence of the electric field), we shall perform MD simulations to obtain the trajectories using the scaled charge of the ions (i.e., ±0.85 for the particular case of the Madrid-2019 force field). In sharp contrast, when the trajectory is analyzed using eqs 1–9, integer charges are used for the ions. The results from this approach are presented for the Madrid-2019 force field in Figure 1 (orange empty squares). As clearly shown, the computed conductivities are closer to the experimental data. These results showcase that a better description is obtained when simultaneously describing both surface, the PES and DMS. However, we do not obtain a perfect agreement with the experimental electrical conductivities of the aqueous solutions. This is not entirely surprising, as the Madrid-2019 force field (that uses a scaled charge of ±0.85) improves the description of transport properties of electrolytes in water but is not able to yield quantitative agreement with experiments. To this end, we have recently proposed a force field for NaCl and KCl (denoted as Madrid-Transport) that is able to predict transport properties of these electrolyte solutions with excellent agreement to the experiment.60,61 Therefore, we shall compute the electrical conductivities of NaCl and KCl solutions using the Madrid-Transport force field (which uses a scaled charge of ±0.75). We shall implement the main idea of this work, namely, to use scaled charges to obtain the trajectories and integer charges to describe the DMS (i.e., using integer charges in eqs 1–9). In Figure 2, we present both properties (viscosities and self-diffusion coefficients of water) in the whole concentration range of each salt up to the experimental solubility limit. Results are independently calculated by two different research groups: Madrid (blue) and Delft (red) are consistent within the error bars. The results are in good agreement with experiments showing that these two transport properties that are obtained from the PES are described satisfactorily by the Madrid-Transport force field.
Figure 2.

Transport properties of NaCl and KCl aqueous solutions at different concentrations obtained with the Madrid-Transport force field by Madrid (blue) and Delft (red) groups at a temperature of T = 298.15 K and pressure of p = 1 bar. (a) Viscosities and (b) self-diffusion coefficients of water (corrected for system size effects). Experimental results have been taken from refs (148 and 149).
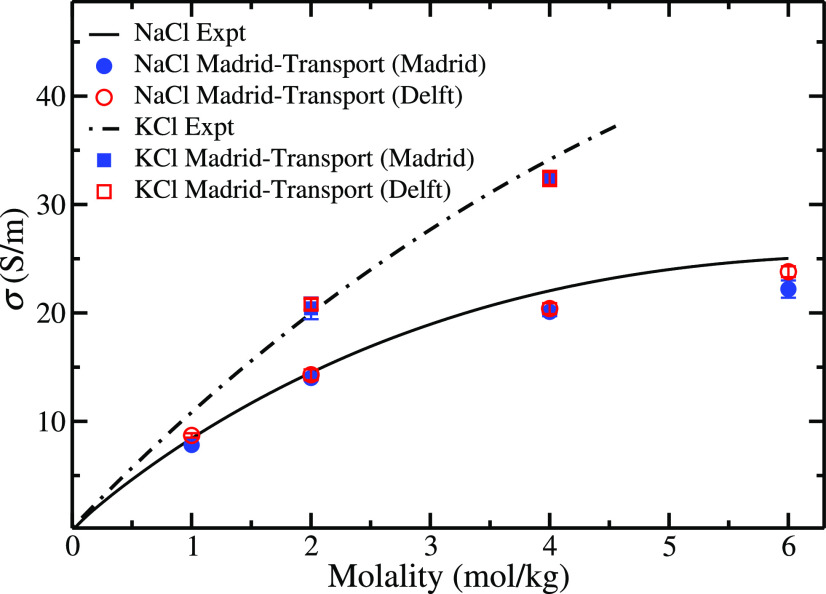
In Figure 3 the results for the electrical conductivities of NaCl and KCl solutions using the Madrid-Transport force field are shown. Note that these results are computed with our novel approach (i.e., using scaled charges q= ±0.75 to describe the trajectories of the system and unit charges to compute the electrical conductivities). We show the results obtained from two different research groups: Madrid (blue) and Delft (red). Both groups adopted the same approach to calculate conductivities (i.e., employing the EH equations) with some minor differences. Madrid has evaluated the conductivity from the mean square dipole displacement, taking into account all the interactions between ions (cation–cation, anion–anion, and cation–anion). Delft has evaluated the Onsager coefficients independently for the cation–cation, anion–anion, and cation–anion interactions and then summed up all the contributions. Both approaches are equivalent and thus should yield identical results. It is important to note that both groups have used different software, constraint algorithms, system sizes, simulation times, and fitting methods (see Simulation Details). Even so, the results for the conductivities obtained by both groups are equal within the error bars. Note also that despite the system sizes used by Delft and Madrid groups being different (between 555 and 4440 water molecules), the electrical conductivities are in agreement, showing that no finite size effects in the computation of electrical conductivities are observed. Nevertheless, since both self-and collective (Maxwell Stefan and Fick) diffusivities exhibit significant finite size effects,121,122,150,151 a thorough investigation for electric conductivities should be also performed. This is particularly important for small concentrations (i.e., below 1 m). This was also previously studied by Shao et al.112 for the JC-SPC/E model concluding that there were not finite size effects when using the Green–Kubo equation. In Figure 3, we can observe that the conductivities obtained by both groups for the Madrid-Transport force field reproduce the experimental conductivities of both NaCl and KCl aqueous solutions over the whole concentration range. Note that the electrical conductivity of KCl is significantly larger than that of NaCl at the same concentration. This difference is correctly described by the Madrid-Transport force field. Thus, the Madrid-Transport force field and the use of scaled charges for the trajectories and integer charges for computing conductivities (i.e., describing the PES with scaled charges and the DMS with integer charges) allows for the first time to correctly reproduce experimental conductivities (and other transport properties as viscosities and water diffusion coefficients). In Tables 1 and 2, we have collected the computed conductivities for each system (by both groups) along with the conductivities obtained by using the NE equation (eq 10) with and without applying the finite-size corrections to the self-diffusion coefficients.
Figure 3.
Electrical conductivities as a function of NaCl concentration obtained with the Madrid-Transport force field in independent research groups: Madrid (blue) using eq 3 and Delft (red) using eq 9, for NaCl (circles) and KCl (squares) aqueous solutions at temperature T = 298.15 K and pressure p = 1 bar. Experimental results have been taken from ref (143).
4.3. Electrical Conductivities by Using the Nernst–Einstein Equation
The correct way to calculate conductivities is to use the Green–Kubo or the Einstein–Helfand equations. However, the NE equation (eq 10) is widely used due to its simplicity. In Tables 1 and 2, the electrical conductivities predicted by the approximate NE formula are also presented. As can be seen, the NE relation overestimates the true conductivity of the model, as obtained from the EH equations. Not surprisingly, the NE equation does not provide the exact value of the electrical conductivity of the model (see the Supporting Information). The reason for this is that it neglects correlations between different ions. The deviations increase with the concentration but they are clearly visible even at a concentration of 1 m. Our results suggest that correlations between different ions tend to decrease the value of the electrical conductivity. The conclusion from the results of Tables 1 and 2 is that NE should not be used to estimate electrical conductivities, as it provides incorrect results. If one wants to compute the true conductivity of a force field, either the GK or EH expressions should be used.
Despite being inaccurate, the NE expression is often used in many papers to obtain electrical conductivities. There are two main reasons for this. The first one is that the calculation of self-diffusion coefficients is relatively easy and computationally cheap. Thus, if the NE formalism is used, then the electrical conductivities are obtained with no additional computational cost. Diffusion coefficients have good statistics, as one can accumulate the statistics of each individual ion, while the EH is expensive, as it is a global property and each configuration contributes a single value of the correlation function. In short, diffusion coefficients of ions can be obtained with good accuracy in runs of 20 ns, whereas ca. 600 ns is needed to have reasonable statistics of the electrical conductivity. Additionally, the computation of the diffusion coefficient is implemented in many MD packages, but this is not the case for the electrical conductivity. The second reason why NE is so popular is because most of the force fields tend to underestimate significantly the electrical conductivity compared to the experiments when they are computed rigorously from the EH formalism. However, since NE electrical conductivities are much larger, they tend to be in better agreement with the experimental results. This creates the paradox that despite NE tends to overestimate the electric conductivities, in many cases, it is closer to experimental data, and thus, there is a resistance to abandon its use. Obviously, this apparent agreement arises from a cancellation of errors (i.e., a poor force field along with a poor way of computing the actual conductivity of the force field can provide good agreement with experiments). This is illustrated in Figure 4, where the electrical conductivities of the JC-SPC/E and SD-SPC/E obtained from NE and from EH are compared to the experimental. As it can be seen, the agreement is better with NE. As we have shown, NE does not describe correctly the electrical conductivity of the force field so that the apparent improvement is obtained from fortuitous cancellation of two errors (the force field and the way to compute the electrical conductivity). Another “apparent” advantage of the NE formalism is that since diffusion coefficients are quite sensitive to the size of the system, one can often find a system size for which the agreement with experiment is excellent. This adds another degree of freedom for “fine-tuning” the final value of the electric conductivity. However, this should not be accepted when striving for an accurate computation of properties. This becomes even more pronounced by the fact that the system size dependency of the electrical conductivity when computed from the EH formalism is quite small as it has been shown in this work (i.e., compare the results from Madrid and from Delft) and also shown in other works.112
Figure 4.

Electrical conductivities as a function of NaCl concentration obtained with different models studied in this work by two different methodologies (i.e., by using the EH relation and the Nernst–Einstein equation) at T = 298.15 K, p = 1 bar. (a) JC-SPC/E (b) SD-SPC/E. Experimental results have been taken from ref (143).
After this work, we strongly advise against using NE when one can actually compute the conductivity using rigorous ways. NE can be used when one has no access to such a computation or when a quick estimation of the order of magnitude of the conductivity is needed. However, even in such cases, the researcher should keep in mind that the NE value is overestimated with respect to the real conductivity. However, we suggest an approximate (and not rigorous) way of at least correcting NE results. The idea is simple. We have analyzed the typical ratio between the electrical conductivities obtained rigorously (i.e., EH relation) and those obtained from the approximate NE formalism and have analyzed whether it is approximately constant for different force fields and concentrations. When computing the electrical conductivity from NE, we used the finite size corrected diffusion coefficients. In this way, the NE conductivities computed here are determined using one of the most correct approaches to estimate diffusion coefficients in the thermodynamic limit. In Figure 5, we show the ratio between the conductivities obtained by EH divided by the conductivities calculated with NE as a function of the concentration. Notice that for models with different charges (JC-SPC/E, Madrid-2019 and Madrid-Transport), for all concentrations and even for both studied salts (NaCl and KCl), the conductivities using the EH equation are about 30% lower than those when using the NE equation. Thus, a rough approximation of the EH conductivities can be obtained simply by employing:
| 15 |
where σEH is the conductivity rigorously computed by using the EH relation, and σNE+YH is the approximate conductivity calculated with the NE equation (after including Yeh–Hummer corrections to the values of the diffusion coefficients). If one wants to roughly estimate the correct conductivities of a model (i.e., evaluated by the EH relation), one can employ only the NE equation and then apply our rule described in eq 15. In this way, one can obtain an approximate (with a typical error of about 5–8%) but still reasonable estimate of the true conductivity of the force field under consideration from the initial guess provided by the NE relation. In fact, regarding the recent work from Gullbrekken et al.,144 this rule also works properly for their results. Note also that this scaling factor in eq 15 (0.7) is empirical and is not related to the charge of ions in the force field. In any case, we recommend to evaluate properly the conductivities by using the GK or EH relations without any approximation to obtain rigorously the correct conductivity of the force field.
Figure 5.
Ratio between the conductivities obtained by using the Einstein–Helfand formula (σEH) and the Nernst–Einstein equation (σNE+YH).
5. Conclusions
In this work, we evaluated the electrical conductivities of NaCl and KCl aqueous solutions up to their solubility limit by using the Einstein–Helfand equation. We have computed the electrical conductivities of four different NaCl force fields (i.e., JC-SPC/E, SD-SPC/E, Madrid-2019, and Madrid-Transport). We have shown that force fields with integer charges are not able to reproduce electrical conductivities, as they underestimate them considerably. Note that for these models integer charges are used to describe both the PES and the DMS. We tested a new approach that is based on the more general idea that different charges should be used to reproduce correctly the PES and the DMS. To implement this idea, we used the Madrid-Transport force field for NaCl and KCl (with scaled charges of ±0.75 for the ions) to obtain the trajectories of the system in the absence of an external electric field. The EH equation is used with integer charges for the ions. The basic idea is that scaled charges describe the PES better, and integer charges describe the DMS more accurately, as was suggested some time ago.117,119 By using this approach, we have shown that the Madrid-Transport force field (a model that provides excellent results for transport properties such as viscosities and diffusion coefficients) reproduces the electrical conductivities of NaCl and KCl for the whole concentration range. Certainly, one can argue that it is possible to use a model with q = ±1 to describe the PES and with q higher than ±1 for describing the DMS. By using this idea (developed in this work) the agreement with experiments for electrical conductivities will also improve for models that use integer charges for the PES. However, the cost of that is that the transported charge will not be 1 e, a result that has no physical meaning. In addition, the force field with that charge would not reproduce the viscosities and self-diffusion coefficients of water as in the rest of the unit charge models. It seems therefore that to reproduce the DMS one should use the integer charge that actually is transported (1 e), but in contrast, for describing the PES, one can use scaled charges to better describe the relative weight of some configurations with respect to others. What does quantum chemistry say about the value of the charge that is indeed transported? Is it correct to assume formal integer charges when computing electrical conductivities? This issue has been discussed in two important papers.115,152 For simplicity we shall discuss this issue using the Green–Kubo formalism,153,154 but one could also use the totally equivalent Helfand–Einstein relation. The electrical conductivity can be rigorously computed from ab initio calculations using the following expression:
| 16 |
where j⃗i is the current density vector, which is defined as
| 17 |
Apparently everything seems normal, but now comes the first surprise. The charge Qi*(t) is not a scalar but a time dependent tensor with components given by
| 18 |
where α, β = x, y, z and ri,β refers to the component β of the vector defining the position of ion i and Mα is the α component of the dipole moment of the system. It should not come as a surprise that the value of the charge of the ion for the calculation of the conductivity comes from derivatives of the dipole moment of the system, which is well-defined and not from arbitrary schemes partitioning the electronic density among the different ions of the system (as for instance the Bader method155,156). However, it has been shown115,152 that one can obtain the rigorous value of the conductivities using a nontime dependent scalar for the charge of ion i (usually denoted as the topological charge qi,top). This is summarized in the following equations:
| 19 |
| 20 |
The conclusion is that although the charge of an ion is a time dependent tensor, there is a nontime dependent scalar value of the charge (denoted as the topological charge) that leads to the correct value of the electrical conductivity. Finally, Grasselli and Baroni,115 and French et al.152 have shown that the value of the topological charge is just the value of the formal charge. Quantum chemistry supports the use of a formal integer charge (i.e., 1 e for monovalent ions) in the calculation of the electrical conductivity. One should not use different values of the formal charge when computing electrical conductivities. That is what we have done in this work. However, quantum chemistry does not say anything about the charge that better fits the PES as it should be regarded as a fitting parameter of the force field, and we have shown that for aqueous electrolyte solutions, the scaled charge with value 0.75 e provides an excellent description of transport properties.
Finally, we have shown that when using the Nernst–Einstein equation, the electrical conductivities are incorrectly calculated due to the neglect of the correlation between different ions, showing discrepancies even at low concentrations. We propose a rule of thumb to obtain a rough estimate of the EH conductivities. The recipe is simple. It consists of multiplying by 0.7 the conductivity obtained from the NE equation (after applying YH corrections to the values of the diffusion coefficients of the individual ions). Nevertheless, this is an approximate correction, and our advice is to use the correct expression (i.e., EH or GK) to obtain rigorously the electrical conductivity of a certain force field.
The results presented in this work independently obtained by two research groups could be useful in the future as benchmark results to be reproduced by groups interested in computing the electrical conductivities of electrolyte solutions. The success of the Madrid-Transport force field in reproducing the transport properties of NaCl and KCl solutions can be regarded as a work-case example showing how fruitful the idea of using different charges to describe the PES and DMS can be in the future. The community performing classical simulations should benefit from this “mental” flexibility. In fact, the community performing ab initio calculations is already using them in an effective way as they are using different fitting parameters when developing neural networks for the PES and the DMS.157,158 Why should we not realize that we can do the same with our force fields?
Acknowledgments
This project has been funded by grant PID2019-105898GB-C21 and grant PID2022-136919NB-C31 of the MICINN. This work was sponsored by NWO Domain Science for the use of supercomputer facilities. O. A. Moultos gratefully acknowledges the support of NVIDIA Corporation with the donation of the Titan V GPU used for this research.
Data Availability Statement
The data that support the findings of this study are available within the article and in the SI.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.3c00562.
Mean square dipole displacement in function of time for different seeds of an aqueous NaCl 4 m solution at 298.15 K and 1 bar by using the Madrid-Transport force field, results for the self-diffusion coefficients of Na+ and Cl+ and electrical conductivities calculated with the Nernst–Einstein approximation and by using the Einstein–Helfand equation, computed electrical conductivities of aqueous NaCl solutions from the EH relations for different molalities, computed electrical conductivities of aqueous KCl solutions from the EH relations for different molalities, contributions to the electrical conductivities computed by the individual Onsager coefficients of aqueous NaCl solutions from the EH relations for different molalities, and contributions to the electrical conductivities computed by the individual Onsager coefficients of aqueous NaCl solutions from the EH relations for different molalities (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Robinson R. A.; Stokes R. H.. Electrolyte solutions; Courier Corporation, 2002. [Google Scholar]
- Attias R.; Salama M.; Hirsch B.; Goffer Y.; Aurbach D. Anode-electrolyte interfaces in secondary magnesium batteries. Joule 2019, 3, 27–52. 10.1016/j.joule.2018.10.028. [DOI] [Google Scholar]
- Logan E.; Dahn J. Electrolyte design for fast-charging Li-ion batteries. Trends in Chemistry 2020, 2, 354–366. 10.1016/j.trechm.2020.01.011. [DOI] [Google Scholar]
- Li M.; Wang C.; Chen Z.; Xu K.; Lu J. New concepts in electrolytes. Chem. Rev. 2020, 120, 6783–6819. 10.1021/acs.chemrev.9b00531. [DOI] [PubMed] [Google Scholar]
- Srimuk P.; Su X.; Yoon J.; Aurbach D.; Presser V. Charge-transfer materials for electrochemical water desalination, ion separation and the recovery of elements. Nature Reviews Materials 2020, 5, 517–538. 10.1038/s41578-020-0193-1. [DOI] [Google Scholar]
- Enderby J.; Neilson G. The structure of electrolyte solutions. Rep. Prog. Phys. 1981, 44, 593. 10.1088/0034-4885/44/6/001. [DOI] [Google Scholar]
- Barthel J. M.; Krienke H.; Kunz W.. Physical chemistry of electrolyte solutions: modern aspects; Springer Science & Business Media, 1998; Vol. 5. [Google Scholar]
- Kirkwood J. G. On the theory of strong electrolyte solutions. J. Chem. Phys. 1934, 2, 767–781. 10.1063/1.1749393. [DOI] [Google Scholar]
- Pitzer K. S.; Press C.. Activity coefficients in electrolyte solutions; CRC Press: Boca Raton, FL, 1991; Vol. 2. [Google Scholar]
- Sangster M.; Dixon M. Interionic potentials in alkali halides and their use in simulations of the molten salts. Adv. Phys. 1976, 25, 247–342. 10.1080/00018737600101392. [DOI] [Google Scholar]
- Adams M. E.; McDonald I. R.; Singer K. Collective dynamical properties of molten salts: molecular dynamics calculations on sodium chloride. Proc. R. Soc. London A 1977, 357, 37–57. 10.1098/rspa.1977.0154. [DOI] [Google Scholar]
- Heinzinger K.; Vogel P. A Molecular Dynamics Study of Aqueous Solutions I. First Results for LiCl in H20. Z. Naturforsch sect. A 1974, 29, 1164–1171. 10.1515/zna-1974-0809. [DOI] [Google Scholar]
- Vogel P.; Heinzinger K. A Molecular Dynamics Study of Aqueous Solutions II. Cesium Chloride in H2O. Z. Naturforsch sect. A 1975, 30, 789–796. 10.1515/zna-1975-6-711. [DOI] [Google Scholar]
- Heinzinger K.; Vogel P. A Molecular Dynamics Study of Aqueous Solutions. III. A Comparison of Selected Alkali Halides. Z. Naturforsch sect. A 1976, 31, 463–475. 10.1515/zna-1976-0508. [DOI] [Google Scholar]
- Bernal J. D.; Fowler R. H. A Theory of Water and Ionic Solutions, with Particular Reference to Hydrogen and Hydroxyl Ions. J. Chem. Phys. 1933, 1, 515. 10.1063/1.1749327. [DOI] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Mahoney M.; Jorgensen W. L. Quantum, intramolecular flexibility, and polarizability effects on the reproduction of the density anomaly of liquid water by simple potential functions. J. Chem. Phys. 2001, 115, 10758–10768. 10.1063/1.1418243. [DOI] [Google Scholar]
- Berendsen H. J. C.; Grigera J. R.; Straatsma T. P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. 10.1021/j100308a038. [DOI] [Google Scholar]
- Horn H. W.; Swope W. C.; Pitera J. W.; Madura J. D.; Dick T. J.; Hura G. L.; Head-Gordon T. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004, 120, 9665–9678. 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
- Abascal J. L. F.; Vega C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. 10.1063/1.2121687. [DOI] [PubMed] [Google Scholar]
- Vega C.; Abascal J. L. F. Simulating water with rigid non-polarizable models: a general perspective. Phys. Chem. Chem. Phys. 2011, 13, 19663–19688. 10.1039/c1cp22168j. [DOI] [PubMed] [Google Scholar]
- Tazi S.; Boţan A.; Salanne M.; Marry V.; Turq P.; Rotenberg B. Diffusion coefficient and shear viscosity of rigid water models. J. Phys.: Condens. Matter 2012, 24, 284117. 10.1088/0953-8984/24/28/284117. [DOI] [PubMed] [Google Scholar]
- González M. A.; Abascal J. L. F. The shear viscosity of rigid water models. J. Chem. Phys. 2010, 132, 096101. 10.1063/1.3330544. [DOI] [PubMed] [Google Scholar]
- Blazquez S.; Vega C. Melting points of water models: Current situation. J. Chem. Phys. 2022, 156, 216101. 10.1063/5.0093815. [DOI] [PubMed] [Google Scholar]
- Jiang H.; Moultos O. A.; Economou I. G.; Panagiotopoulos A. Z. Hydrogen-bonding polarizable intermolecular potential model for water. J. Phys. Chem. B 2016, 120, 12358–12370. 10.1021/acs.jpcb.6b08205. [DOI] [PubMed] [Google Scholar]
- Reddy S. K.; Straight S. C.; Bajaj P.; Huy Pham C.; Riera M.; Moberg D. R.; Morales M. A.; Knight C.; Götz A. W.; Paesani F. On the accuracy of the MB-pol many-body potential for water: Interaction energies, vibrational frequencies, and classical thermodynamic and dynamical properties from clusters to liquid water and ice. J. Chem. Phys. 2016, 145, 194504. 10.1063/1.4967719. [DOI] [PubMed] [Google Scholar]
- Kiss P. T.; Baranyai A. A systematic development of a polarizable potential of water. J. Chem. Phys. 2013, 138, 204507. 10.1063/1.4807600. [DOI] [PubMed] [Google Scholar]
- Smith W. R.; Nezbeda I.; Kolafa J.; Moučka F. Recent progress in the molecular simulation of thermodynamic properties of aqueous electrolyte solutions. Fluid Phase Equilib. 2018, 466, 19–30. 10.1016/j.fluid.2018.03.006. [DOI] [Google Scholar]
- Chandrasekhar J.; Spellmeyer D. C.; Jorgensen W. L. Energy component analysis for dilute aqueous solutions of lithium (1+), sodium (1+), fluoride (1-), and chloride (1-) ions. J. Am. Chem. Soc. 1984, 106, 903–910. 10.1021/ja00316a012. [DOI] [Google Scholar]
- Straatsma T.; Berendsen H. Free energy of ionic hydration: Analysis of a thermodynamic integration technique to evaluate free energy differences by molecular dynamics simulations. J. Chem. Phys. 1988, 89, 5876–5886. 10.1063/1.455539. [DOI] [Google Scholar]
- Aqvist J. Ion-water interaction potentials derived from free energy perturbation simulations. J. Phys. Chem. 1990, 94, 8021–8024. 10.1021/j100384a009. [DOI] [Google Scholar]
- Dang L. X. Development of nonadditive intermolecular potentials using molecular dynamics: solvation of Li+ and F− ions in polarizable water. J. Chem. Phys. 1992, 96, 6970–6977. 10.1063/1.462555. [DOI] [Google Scholar]
- Beglov D.; Roux B. Finite representation of an infinite bulk system: solvent boundary potential for computer simulations. J. Chem. Phys. 1994, 100, 9050–9063. 10.1063/1.466711. [DOI] [Google Scholar]
- Smith D. E.; Dang L. X. Computer simulations of NaCl association in polarizable water. J. Chem. Phys. 1994, 100, 3757–3766. 10.1063/1.466363. [DOI] [Google Scholar]
- Roux B. Valence selectivity of the gramicidin channel: a molecular dynamics free energy perturbation study. Biophys. J. 1996, 71, 3177–3185. 10.1016/S0006-3495(96)79511-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng Z.; Ewig C. S.; Hwang M.-J.; Waldman M.; Hagler A. T. Derivation of class II force fields. 4. van der Waals parameters of Alkali metal cations and Halide anions. J. Phys. Chem. A 1997, 101, 7243–7252. 10.1021/jp964080y. [DOI] [Google Scholar]
- Weerasinghe S.; Smith P. E. A Kirkwood–Buff derived force field for sodium chloride in water. J. Chem. Phys. 2003, 119, 11342–11349. 10.1063/1.1622372. [DOI] [Google Scholar]
- Jensen K. P.; Jorgensen W. L. Halide, ammonium, and alkali metal ion parameters for modeling aqueous solutions. J. Chem. Theory Comput. 2006, 2, 1499–1509. 10.1021/ct600252r. [DOI] [PubMed] [Google Scholar]
- Lamoureux G.; Roux B. Absolute hydration free energy scale for alkali and halide ions established from simulations with a polarizable force field. J. Phys. Chem. B 2006, 110, 3308–3322. 10.1021/jp056043p. [DOI] [PubMed] [Google Scholar]
- Alejandre J.; Hansen J.-P. Ions in water: From ion clustering to crystal nucleation. Phys. Rev. E 2007, 76, 061505. 10.1103/PhysRevE.76.061505. [DOI] [PubMed] [Google Scholar]
- Lenart P. J.; Jusufi A.; Panagiotopoulos A. Z. Effective potentials for 1:1 electrolyte solutions incorporating dielectric saturation and repulsive hydration. J. Chem. Phys. 2007, 126, 044509. 10.1063/1.2431169. [DOI] [PubMed] [Google Scholar]
- Joung I. S.; Cheatham T. E. Determination of alkali and halide monovalent Ion Parameters for Use in Explicit Solvated Biomolecular Simulation. J. Phys. Chem. B 2008, 112, 9020. 10.1021/jp8001614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corradini D.; Rovere M.; Gallo P. A route to explain water anomalies from results on an aqueous solution of salt. J. Chem. Phys. 2010, 132, 134508. 10.1063/1.3376776. [DOI] [PubMed] [Google Scholar]
- Callahan K. M.; Casillas-Ituarte N. N.; Roeselová M.; Allen H. C.; Tobias D. J. Solvation of magnesium dication: molecular dynamics simulation and vibrational spectroscopic study of magnesium chloride in aqueous solutions. J. Phys. Chem. A 2010, 114, 5141–5148. 10.1021/jp909132a. [DOI] [PubMed] [Google Scholar]
- Yu H.; Whitfield T. W.; Harder E.; Lamoureux G.; Vorobyov I.; Anisimov V. M.; MacKerell A. D. Jr; Roux B. Simulating monovalent and divalent ions in aqueous solution using a Drude polarizable force field. J. Chem. Theory Comput. 2010, 6, 774–786. 10.1021/ct900576a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reif M. M.; Hünenberger P. H. Computation of methodology-independent single-ion solvation properties from molecular simulations. IV. Optimized Lennard-Jones interaction parameter sets for the alkali and halide ions in water. J. Chem. Phys. 2011, 134, 144104. 10.1063/1.3567022. [DOI] [PubMed] [Google Scholar]
- Gee M. B.; Cox N. R.; Jiao Y.; Bentenitis N.; Weerasinghe S.; Smith P. E. A Kirkwood-Buff derived force field for aqueous alkali halides. J. Chem. Theory Comput. 2011, 7, 1369–1380. 10.1021/ct100517z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benavides A. L.; Portillo M. A.; Chamorro V. C.; Espinosa J. R.; Abascal J. L. F.; Vega C. A potential model for sodium chloride solutions based on the TIP4P/2005 water model. J. Chem. Phys. 2017, 147, 104501. 10.1063/1.5001190. [DOI] [PubMed] [Google Scholar]
- Deublein S.; Vrabec J.; Hasse H. A set of molecular models for alkali and halide ions in aqueous solution. J. Chem. Phys. 2012, 136, 084501. 10.1063/1.3687238. [DOI] [PubMed] [Google Scholar]
- Mao A. H.; Pappu R. V. Crystal lattice properties fully determine short-range interaction parameters for alkali and halide ions. J. Chem. Phys. 2012, 137, 064104. 10.1063/1.4742068. [DOI] [PubMed] [Google Scholar]
- Mamatkulov S.; Fyta M.; Netz R. R. Force fields for divalent cations based on single-ion and ion-pair properties. J. Chem. Phys. 2013, 138, 024505. 10.1063/1.4772808. [DOI] [PubMed] [Google Scholar]
- Moučka F.; Nezbeda I.; Smith W. R. Molecular force field development for aqueous electrolytes: 1. Incorporating appropriate experimental data and the inadequacy of simple electrolyte force fields based on Lennard-Jones and point charge interactions with Lorentz–Berthelot rules. J. Chem. Theory Comput. 2013, 9, 5076–5085. 10.1021/ct4006008. [DOI] [PubMed] [Google Scholar]
- Kiss P. T.; Baranyai A. A new polarizable force field for alkali and halide ions. J. Chem. Phys. 2014, 141, 114501. 10.1063/1.4895129. [DOI] [PubMed] [Google Scholar]
- Kolafa J. Solubility of NaCl in water and its melting point by molecular dynamics in the slab geometry and a new BK3-compatible force field. J. Chem. Phys. 2016, 145, 204509. 10.1063/1.4968045. [DOI] [PubMed] [Google Scholar]
- Elfgen R.; Hülsmann M.; Krämer A.; Köddermann T.; Kirschner K. N.; Reith D. Optimized atomistic force fields for aqueous solutions of Magnesium and Calcium Chloride: Analysis, achievements and limitations. Eur. Phys. J. Spec. Top. 2016, 225, 1391–1409. 10.1140/epjst/e2016-60112-7. [DOI] [Google Scholar]
- Pethes I. A comparison of classical interatomic potentials applied to highly concentrated aqueous lithium chloride solutions. J. Mol. Liq. 2017, 242, 845–858. 10.1016/j.molliq.2017.07.076. [DOI] [Google Scholar]
- Yagasaki T.; Matsumoto M.; Tanaka H. Lennard-Jones parameters determined to reproduce the solubility of NaCl and KCl in SPC/E, TIP3P, and TIP4P/2005 water. J. Chem. Theory Comput. 2020, 16, 2460. 10.1021/acs.jctc.9b00941. [DOI] [PubMed] [Google Scholar]
- Zeron I. M.; Abascal J. L. F.; Vega C. A force field of Li+, Na., K+, Mg2+, Ca2+, Cl– and SO42– in aqueous solution based on the TIP4P/2005 water model and scaled charges for the ions. J. Chem. Phys. 2019, 151, 134504. 10.1063/1.5121392. [DOI] [PubMed] [Google Scholar]
- Blazquez S.; Conde M. M.; Abascal J. L. F.; Vega C. The Madrid-2019 force field for electrolytes in water using TIP4P/2005 and scaled charges: Extension to the ions F–, Br–, I–, Rb+, and Cs+. J. Chem. Phys. 2022, 156, 044505. 10.1063/5.0077716. [DOI] [PubMed] [Google Scholar]
- Habibi P.; Rahbari A.; Blazquez S.; Vega C.; Dey P.; Vlugt T. J. H.; Moultos O. A. A New Force Field for OH– for Computing Thermodynamic and Transport Properties of H2 and O2 in Aqueous NaOH and KOH Solutions. J.Phys.Chem.B 2022, 126, 9376. 10.1021/acs.jpcb.2c06381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blazquez S.; Conde M. M.; Vega C. Scaled charges for ions: and improvement but not the final word for modeling electrolytes in water. J. Chem. Phys. 2023, 158, 054505. 10.1063/5.0136498. [DOI] [PubMed] [Google Scholar]
- Panagiotopoulos A. Z. Simulations of activities, solubilities, transport properties, and nucleation rates for aqueous electrolyte solutions. J. Chem. Phys. 2020, 153, 010903. 10.1063/5.0012102. [DOI] [PubMed] [Google Scholar]
- Leontyev I. V.; Stuchebrukhov A. A. Electronic continuum model for molecular dynamics simulations. J. Chem. Phys. 2009, 130, 085102. 10.1063/1.3060164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontyev I. V.; Stuchebrukhov A. A. Electronic polarizability and the effective pair potentials of water. J. Chem. Theory Comput. 2010, 6, 3153–3161. 10.1021/ct1002048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontyev I. V.; Stuchebrukhov A. A. Electronic continuum model for molecular dynamics simulations of biological molecules. J. Chem. Theory Comput. 2010, 6, 1498–1508. 10.1021/ct9005807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontyev I. V.; Stuchebrukhov A. A. Accounting for electronic polarization in non-polarizable force fields. Phys. Chem. Chem. Phys. 2011, 13, 2613–2626. 10.1039/c0cp01971b. [DOI] [PubMed] [Google Scholar]
- Leontyev I. V.; Stuchebrukhov A. A. Polarizable mean-field model of water for biological simulations with AMBER and CHARMM force fields. J. Chem. Theory Comput. 2012, 8, 3207–3216. 10.1021/ct300011h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontyev I. V.; Stuchebrukhov A. A. Polarizable molecular interactions in condensed phase and their equivalent nonpolarizable models. J. Chem. Phys. 2014, 141, 014103. 10.1063/1.4884276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kann Z.; Skinner J. A scaled-ionic-charge simulation model that reproduces enhanced and suppressed water diffusion in aqueous salt solutions. J. Chem. Phys. 2014, 141, 104507. 10.1063/1.4894500. [DOI] [PubMed] [Google Scholar]
- Pluhařová E.; Mason P. E.; Jungwirth P. Ion pairing in aqueous lithium salt solutions with monovalent and divalent counter-anions. J. Phys. Chem. A 2013, 117, 11766–11773. 10.1021/jp402532e. [DOI] [PubMed] [Google Scholar]
- Kohagen M.; Mason P. E.; Jungwirth P. Accurate description of calcium solvation in concentrated aqueous solutions. J. Phys. Chem. B 2014, 118, 7902–7909. 10.1021/jp5005693. [DOI] [PubMed] [Google Scholar]
- Kohagen M.; Mason P. E.; Jungwirth P. Accounting for electronic polarization effects in aqueous sodium chloride via molecular dynamics aided by neutron scattering. J. Phys. Chem. B 2016, 120, 1454–1460. 10.1021/acs.jpcb.5b05221. [DOI] [PubMed] [Google Scholar]
- Duboué-Dijon E.; Mason P. E.; Fischer H. E.; Jungwirth P. Hydration and ion pairing in aqueous Mg2+ and Zn2+ solutions: force-field description aided by neutron scattering experiments and ab initio molecular dynamics simulations. J. Phys. Chem. B 2018, 122, 3296–3306. 10.1021/acs.jpcb.7b09612. [DOI] [PubMed] [Google Scholar]
- Martinek T.; Duboué-Dijon E.; Timr v.; Mason P. E.; Baxová K.; Fischer H. E.; Schmidt B.; Pluhařová E.; Jungwirth P. Calcium ions in aqueous solutions: Accurate force field description aided by ab initio molecular dynamics and neutron scattering. J. Chem. Phys. 2018, 148, 222813. 10.1063/1.5006779. [DOI] [PubMed] [Google Scholar]
- Fuentes-Azcatl R.; Barbosa M. C. Sodium chloride, nacl/ε: New force field. J. Phys. Chem. B 2016, 120, 2460–2470. 10.1021/acs.jpcb.5b12584. [DOI] [PubMed] [Google Scholar]
- Fuentes-Azcatl R.; Barbosa M. C. Potassium bromide, KBr/ε: New Force Field. Phys. A 2018, 491, 480–489. 10.1016/j.physa.2017.09.081. [DOI] [Google Scholar]
- Li J.; Wang F. Pairwise-additive force fields for selected aqueous monovalent ions from adaptive force matching. J. Chem. Phys. 2015, 143, 194505. 10.1063/1.4935599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruce E. E.; van der Vegt N. F. A. Does an electronic continuum correction improve effective short-range ion-ion interactions in aqueous solution?. J. Chem. Phys. 2018, 148, 222816. 10.1063/1.5017101. [DOI] [PubMed] [Google Scholar]
- Yao Y.; Berkowitz M. L.; Kanai Y. Communication: Modeling of concentration dependent water diffusivity in ionic solutions: Role of intermolecular charge transfer. J. Chem. Phys. 2015, 143, 241101. 10.1063/1.4938083. [DOI] [PubMed] [Google Scholar]
- Soniat M.; Rick S. W. The effects of charge transfer on the aqueous solvation of ions. J. Chem. Phys. 2012, 137, 044511. 10.1063/1.4736851. [DOI] [PubMed] [Google Scholar]
- Lee A. J.; Rick S. W. The effects of charge transfer on the properties of liquid water. J. Chem. Phys. 2011, 134, 184507. 10.1063/1.3589419. [DOI] [PubMed] [Google Scholar]
- Soniat M.; Rick S. W. Charge transfer effects of ions at the liquid water/vapor interface. J. Chem. Phys. 2014, 140, 184703. 10.1063/1.4874256. [DOI] [PubMed] [Google Scholar]
- Soniat M.; Pool G.; Franklin L.; Rick S. W. Ion association in aqueous solution. Fluid Phase Equilib. 2016, 407, 31–38. 10.1016/j.fluid.2015.05.001. [DOI] [Google Scholar]
- Le Breton G.; Joly L. Molecular modeling of aqueous electrolytes at interfaces: Effects of long-range dispersion forces and of ionic charge rescaling. J. Chem. Phys. 2020, 152, 241102. 10.1063/5.0011058. [DOI] [PubMed] [Google Scholar]
- Blazquez S.; Zeron I. M.; Conde M. M.; Abascal J. L. F.; Vega C. Scaled charges at work: Salting out and interfacial tension of methane with electrolyte solutions from computer simulations. Fluid Phase Equilib. 2020, 513, 112548. 10.1016/j.fluid.2020.112548. [DOI] [Google Scholar]
- Sedano L. F.; Blazquez S.; Noya E. G.; Vega C.; Troncoso J. Maximum in density of electrolyte solutions: Learning about ion-water interactions and testing the Madrid-2019 force field. J. Chem. Phys. 2022, 156, 154502. 10.1063/5.0087679. [DOI] [PubMed] [Google Scholar]
- Lamas C. P.; Vega C.; Noya E. G. Freezing point depression of salt aqueous solutions using the Madrid-2019 model. J. Chem. Phys. 2022, 156, 134503. 10.1063/5.0085051. [DOI] [PubMed] [Google Scholar]
- Zeron I. M.; Gonzalez M. A.; Errani E.; Vega C.; Abascal J. L. F. “In Silico” Seawater. J. Chem. Theory Comput. 2021, 17, 1715–1725. 10.1021/acs.jctc.1c00072. [DOI] [PubMed] [Google Scholar]
- Kim J. S.; Wu Z.; Morrow A. R.; Yethiraj A.; Yethiraj A. Self-diffusion and viscosity in electrolyte solutions. J. Phys. Chem. B 2012, 116, 12007–12013. 10.1021/jp306847t. [DOI] [PubMed] [Google Scholar]
- van Rooijen W.; Habibi P.; Xu K.; Dey P.; Vlugt T. J. H.; Hajibeygi H.; Moultos O.. Interfacial Tensions, Solubilities, and Transport Properties of the H2/H2O/NaCl System: A Molecular Simulation Study. J. Chem. Eng. Data 2023, 10.1021/acs.jced.2c00707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schröder C.; Haberler M.; Steinhauser O. On the computation and contribution of conductivity in molecular ionic liquids. J. Chem. Phys. 2008, 128, 134501. 10.1063/1.2868752. [DOI] [PubMed] [Google Scholar]
- Picálek J.; Kolafa J. Molecular dynamics study of conductivity of ionic liquids: The Kohlrausch law. J. Mol. Liq. 2007, 134, 29–33. 10.1016/j.molliq.2006.12.015. [DOI] [Google Scholar]
- Nieszporek K.; Nieszporek J.; Trojak M. Calculations of shear viscosity, electric conductivity and diffusion coefficients of aqueous sodium perchlorate solutions from molecular dynamics simulations. Computational and Theoretical Chemistry 2016, 1090, 52–57. 10.1016/j.comptc.2016.06.002. [DOI] [Google Scholar]
- Helfand E. Transport coefficients from dissipation in a canonical ensemble. Phys. Rev. 1960, 119, 1. 10.1103/PhysRev.119.1. [DOI] [Google Scholar]
- Malaspina D. C.; Lisal M.; Larentzos J. P.; Brennan J. K.; Mackie A.; Avalos J. B. Transport coefficients from Einstein-Helfand relations using standard and energy-conserving dissipative particle dynamics methods. Phys. Chem. Chem. Phys. 2023, 25, 12025. 10.1039/D2CP04838H. [DOI] [PubMed] [Google Scholar]
- Celebi A. T.; Vlugt T. J. H.; Moultos O. A. Structural, thermodynamic, and transport properties of aqueous reline and ethaline solutions from molecular dynamics simulations. J. Phys. Chem. B 2019, 123, 11014–11025. 10.1021/acs.jpcb.9b09729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawass N.; Langeveld J.; Ramdin M.; Pérez-Gallent E.; Villanueva A. A.; Giling E. J.; Langerak J.; Van Den Broeke L. J.; Vlugt T. J. H.; Moultos O. A. Solubilities and Transport Properties of CO2, Oxalic Acid, and Formic Acid in Mixed Solvents Composed of Deep Eutectic Solvents, Methanol, and Propylene Carbonate. J. Phys. Chem. B 2022, 126, 3572–3584. 10.1021/acs.jpcb.2c01425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyubartsev A. P.; Laaksonen A. Concentration effects in aqueous NaCl solutions. A molecular dynamics simulation. J. Phys. Chem. 1996, 100, 16410–16418. 10.1021/jp961317h. [DOI] [Google Scholar]
- Allen M. P.; Tildesley D. J.. Computer Simulation of Liquids; Oxford University Press: Oxford, 1987. [Google Scholar]
- Kubisiak P.; Eilmes A. Estimates of Electrical Conductivity from Molecular Dynamics Simulations: How to Invest the Computational Effort. J. Phys. Chem. B 2020, 124, 9680–9689. 10.1021/acs.jpcb.0c07704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loche P.; Steinbrunner P.; Friedowitz S.; Netz R. R.; Bonthuis D. J. Transferable ion force fields in water from a simultaneous optimization of ion solvation and ion–ion interaction. J. Phys. Chem. B 2021, 125, 8581–8587. 10.1021/acs.jpcb.1c05303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu Z.; Jiang J. Assessment of biomolecular force fields for molecular dynamics simulations in a protein crystal. J. Comput. chem. 2009, 31, 371–380. 10.1002/jcc.21330. [DOI] [PubMed] [Google Scholar]
- Yllö A.; Zhang C. Experimental and molecular dynamics study of the ionic conductivity in aqueous LiCl electrolytes. Chem. Phys. Lett. 2019, 729, 6–10. 10.1016/j.cplett.2019.05.004. [DOI] [Google Scholar]
- Zhang Y.; Maginn E. J. Direct correlation between ionic liquid transport properties and ion pair lifetimes: a molecular dynamics study. journal of physical chemistry letters 2015, 6, 700–705. 10.1021/acs.jpclett.5b00003. [DOI] [PubMed] [Google Scholar]
- Krienke H.; Opalka D. Hydration of molecular ions: A molecular dynamics study with a SPC/E water model. J. Phys. Chem. C 2007, 111, 15935–15941. 10.1021/jp073721u. [DOI] [Google Scholar]
- Prasad S.; Chakravarty C.; Kashyap H. K. Concentration-dependent structure and dynamics of aqueous LiCl solutions: a molecular dynamics study. J. Mol. Liq. 2017, 225, 240–250. 10.1016/j.molliq.2016.11.042. [DOI] [Google Scholar]
- Kowsari M.; Alavi S.; Ashrafizaadeh M.; Najafi B. Molecular dynamics simulation of imidazolium-based ionic liquids. II. Transport coefficients. J. Chem. Phys. 2009, 130, 014703. 10.1063/1.3042279. [DOI] [PubMed] [Google Scholar]
- Kowsari M.; Alavi S.; Najafi B.; Gholizadeh K.; Dehghanpisheh E.; Ranjbar F. Molecular dynamics simulations of the structure and transport properties of tetra-butylphosphonium amino acid ionic liquids. Phys. Chem. Chem. Phys. 2011, 13, 8826–8837. 10.1039/c0cp02581j. [DOI] [PubMed] [Google Scholar]
- Mondal A.; Balasubramanian S. A molecular dynamics study of collective transport properties of imidazolium-based room-temperature ionic liquids. Journal of Chemical & Engineering Data 2014, 59, 3061–3068. 10.1021/je500132u. [DOI] [Google Scholar]
- Rey-Castro C.; Vega L. F. Transport properties of the ionic liquid 1-ethyl-3-methylimidazolium chloride from equilibrium molecular dynamics simulation. The effect of temperature. J. Phys. Chem. B 2006, 110, 14426–14435. 10.1021/jp062885s. [DOI] [PubMed] [Google Scholar]
- Sala J.; Guardia E.; Marti J. Effects of concentration on structure, dielectric, and dynamic properties of aqueous NaCl solutions using a polarizable model. J. Chem. Phys. 2010, 132, 214505. 10.1063/1.3429253. [DOI] [PubMed] [Google Scholar]
- Shao Y.; Shigenobu K.; Watanabe M.; Zhang C. Role of viscosity in deviations from the Nernst-Einstein relation. J. Phys. Chem. B 2020, 124, 4774–4780. 10.1021/acs.jpcb.0c02544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W.; Chen X.; Wang Y.; Wu L.; Hu Y. Experimental and modeling of conductivity for electrolyte solution systems. ACS omega 2020, 5, 22465–22474. 10.1021/acsomega.0c03013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moura-Neto M. H.; Monteiro M. F.; Ferreira F. A.; Silva D. J.; Figueiredo C. S.; Ciambelli J. R.; Pereira L. S.; do Nascimento J. F.; Chiavone-Filho O. Density and Electrical Conductivity for Aqueous Mixtures of Monoethylene Glycol and Sodium Chloride: Experimental Data and Data-Driven Modeling for Composition Determination. Journal of Chemical & Engineering Data 2021, 66, 1914–1928. 10.1021/acs.jced.0c00962. [DOI] [Google Scholar]
- Grasselli F.; Baroni S. Topological quantization and gauge invariance of charge transport in liquid insulators. Nat. Phys. 2019, 15, 967–972. 10.1038/s41567-019-0562-0. [DOI] [Google Scholar]
- Pegolo P.; Grasselli F.; Baroni S. Oxidation States, Thouless’ Pumps, and Nontrivial Ionic Transport in Nonstoichiometric Electrolytes. Physical Review X 2020, 10, 041031. 10.1103/PhysRevX.10.041031. [DOI] [Google Scholar]
- Vega C. Water one molecule, two surfaces, one mistake. Mol. Phys. 2015, 113, 1145. 10.1080/00268976.2015.1005191. [DOI] [Google Scholar]
- Predota M.; Biriukov D. Electronic continuum correction without scaled charges. J. Mol. Liq. 2020, 314, 113571. 10.1016/j.molliq.2020.113571. [DOI] [Google Scholar]
- Jorge M.; Lue L. The dielectric constant: Reconciling simulation and experiment. J. Chem. Phys. 2019, 150, 084108. 10.1063/1.5080927. [DOI] [PubMed] [Google Scholar]
- Einstein A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Annalen der physik 1905, 322, 549. 10.1002/andp.19053220806. [DOI] [Google Scholar]
- Yeh I. C.; Hummer G. System-Size Dependence of Diffusion Coefficients and Viscosities from Molecular Dynamics Simulations with Periodic Boundary Conditions. J. Phys. Chem. B 2004, 108, 15873. 10.1021/jp0477147. [DOI] [Google Scholar]
- Celebi A. T.; Jamali S. H.; Bardow A.; Vlugt T. J. H.; Moultos O. A. Finite-size effects of diffusion coefficients computed from molecular dynamics: a review of what we have learned so far. Mol. Simul. 2021, 47, 831–845. 10.1080/08927022.2020.1810685. [DOI] [Google Scholar]
- Moultos O. A.; Zhang Y.; Tsimpanogiannis I. N.; Economou I. G.; Maginn E. J. System-size corrections for self-diffusion coefficients calculated from molecular dynamics simulations: The case of CO2, n-alkanes, and poly (ethylene glycol) dimethyl ethers. J. Chem. Phys. 2016, 145, 074109. 10.1063/1.4960776. [DOI] [PubMed] [Google Scholar]
- Jamali S. H.; Hartkamp R.; Bardas C.; Sohl J.; Vlugt T. J. H.; Moultos O. A. Shear viscosity computed from the finite-size effects of self-diffusivity in equilibrium molecular dynamics. J. Chem. Theory Comput. 2018, 14, 5959–5968. 10.1021/acs.jctc.8b00625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Spoel D.; Lindahl E.; Hess B.; Groenhof G.; Mark A. E.; Berendsen H. J. C. Gromacs: Fast, flexible and free. J. Comput. Chem. 2005, 26, 1701. 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- Beeman D. Some multistep methods for use in molecular dynamics calculations. J. Comput. Phys. 1976, 20, 130–139. 10.1016/0021-9991(76)90059-0. [DOI] [Google Scholar]
- Nosé S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. 10.1080/00268978400101201. [DOI] [Google Scholar]
- Hoover W. G. Canonical dynamics: equilibrium phase-space distributions 1985, 31, 1695–1697. 10.1103/PhysRevA.31.1695. [DOI] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463.. [DOI] [Google Scholar]
- Hess B. P-LINCS: A Parallel Linear Constraint Solver for molecular simulation. J. Chem. Theory Comput. 2008, 4, 116–122. 10.1021/ct700200b. [DOI] [PubMed] [Google Scholar]
- Delft High Performance Computing Centre (DHPC), DelftBlue Supercomputer (Phase 1). https://www.tudelft.nl/dhpc/ark:/44463/DelftBluePhase1, 2022.
- Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
- Ryckaert J. P.; Ciccotti G.; Berendsen H. J. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
- Frenkel D.; Smit B.. Understanding molecular simulation: from algorithms to applications, 2nd ed.; Elsevier: San Diego, 2002. [Google Scholar]
- Hockney R.; Eastwood J.. Computer Simulation Using Particles, 1st ed.; CRC Press: New York, 1988. [Google Scholar]
- Plimpton S.LAMMPS Documentation (15 Sep 2022 version). 2015; https://docs.lammps.org/Manual.html (accessed 26/10/2022).
- Martinez L.; Andrade R.; Birgin E. G.; Martínez J. M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
- Jamali S. H.; Wolff L.; Becker T. M.; de Groen M.; Ramdin M.; Hartkamp R.; Bardow A.; Vlugt T. J. H.; Moultos O. A. OCTP: ATool for On-the-Fly Calculation of Transport Properties of Fluids with the order-n Algorithm in LAMMPS. J. Chem. Inf. Model. 2019, 59, 1290–1294. 10.1021/acs.jcim.8b00939. [DOI] [PubMed] [Google Scholar]
- Dubbeldam D.; Ford D. C.; Ellis D. E.; Snurr R. Q. A new perspective on the order-n algorithm for computing correlation functions. Mol. Simul. 2009, 35, 1084–1097. 10.1080/08927020902818039. [DOI] [Google Scholar]
- Chambers J.; Stokes J. M.; Stokes R. Conductances of concentrated aqueous sodium and potassium chloride solutions at 25. J. Phys. Chem. 1956, 60, 985–986. 10.1021/j150541a040. [DOI] [Google Scholar]
- Gullbrekken Ø.; Røe I. T.; Selbach S. M.; Schnell S. K. Charge Transport in Water–NaCl Electrolytes with Molecular Dynamics Simulations. J. Phys. Chem. B 2023, 127, 2729–2738. 10.1021/acs.jpcb.2c08047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorge M.; Barrera M. C.; Milne A. W.; Ringrose C.; Cole D. J. What is the Optimal Dipole Moment for Nonpolarizable Models of Liquids?. J. Chem. Theory Comput. 2023, 19, 1790–1804. 10.1021/acs.jctc.2c01123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H.; Wang Y.; Bowman J. M. Transferable ab initio dipole moment for water: three applications to bulk water. J. Phys. Chem. B 2016, 120, 1735–1742. 10.1021/acs.jpcb.5b09213. [DOI] [PubMed] [Google Scholar]
- Liu H.; Wang Y.; Bowman J. M. Quantum calculations of the IR spectrum of liquid water using ab initio and model potential and dipole moment surfaces and comparison with experiment. J. Chem. Phys. 2015, 142, 194502. 10.1063/1.4921045. [DOI] [PubMed] [Google Scholar]
- Laliberté M. Model for calculating the viscosity of aqueous solutions. J. Chem. Eng. Data 2007, 52, 321–335. 10.1021/je0604075. [DOI] [Google Scholar]
- Müller K.; Hertz H. A parameter as an indicator for water- water association in solutions of strong electrolytes. J. Phys. Chem. 1996, 100, 1256–1265. 10.1021/jp951303w. [DOI] [Google Scholar]
- Jamali S. H.; Wolff L.; Becker T. M.; Bardow A.; Vlugt T. J. H.; Moultos O. A. Finite-size effects of binary mutual diffusion coefficients from molecular dynamics. J. Chem. Theory Comput. 2018, 14, 2667–2677. 10.1021/acs.jctc.8b00170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jamali S. H.; Bardow A.; Vlugt T. J. H.; Moultos O. A. Generalized form for finite-size corrections in mutual diffusion coefficients of multicomponent mixtures obtained from equilibrium molecular dynamics simulation. J. Chem. Theory Comput. 2020, 16, 3799–3806. 10.1021/acs.jctc.0c00268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- French M.; Hamel S.; Redmer R. Dynamical screening and ionic conductivity in water from ab initio simulations. Physical review letters 2011, 107, 185901. 10.1103/PhysRevLett.107.185901. [DOI] [PubMed] [Google Scholar]
- Hansen J.-P.; McDonald I. R.. Theory of simple liquids: with applications to soft matter; Academic Press, 2013. [Google Scholar]
- Baştuğ T.; Kuyucak S. Temperature dependence of the transport coefficients of ions from molecular dynamics simulations. Chemical physics letters 2005, 408, 84–88. 10.1016/j.cplett.2005.04.012. [DOI] [Google Scholar]
- Bader R.; et al. A quantum theory; Clarendon: Oxford, UK, 1990. [Google Scholar]
- Sanville E.; Kenny S. D.; Smith R.; Henkelman G. Improved grid-based algorithm for Bader charge allocation. Journal of computational chemistry 2007, 28, 899–908. 10.1002/jcc.20575. [DOI] [PubMed] [Google Scholar]
- Krishnamoorthy A.; Nomura K.-i.; Baradwaj N.; Shimamura K.; Rajak P.; Mishra A.; Fukushima S.; Shimojo F.; Kalia R.; Nakano A.; et al. Dielectric constant of liquid water determined with neural network quantum molecular dynamics. Phys. Rev. Lett. 2021, 126, 216403. 10.1103/PhysRevLett.126.216403. [DOI] [PubMed] [Google Scholar]
- Piaggi P. M.; Weis J.; Panagiotopoulos A. Z.; Debenedetti P. G.; Car R. Homogeneous ice nucleation in an ab initio machine-learning model of water. Proc. Natl. Acad. Sci. U. S. A. 2022, 119, e2207294119. 10.1073/pnas.2207294119. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available within the article and in the SI.