FIG. 4.

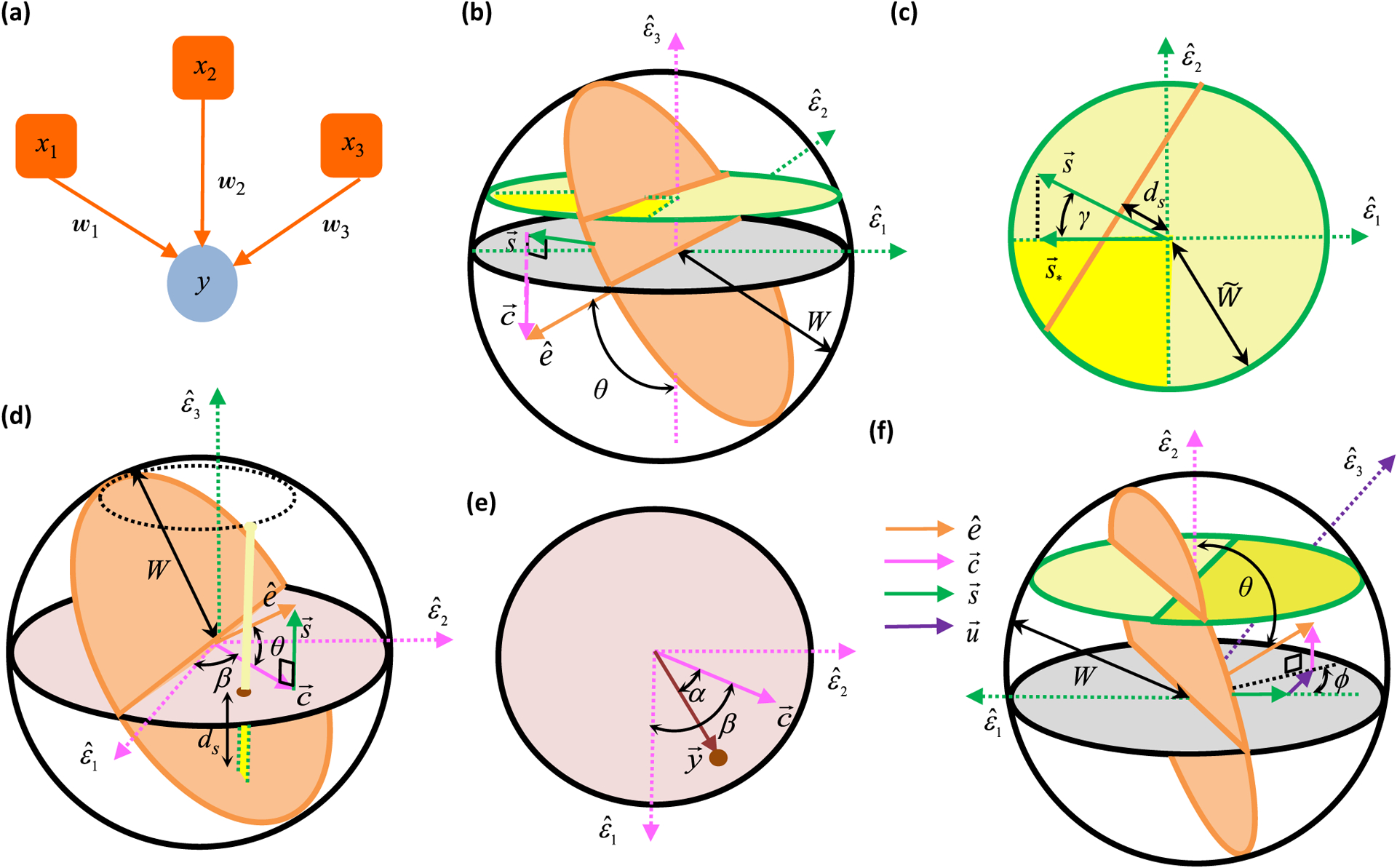
Geometric quantities determining whether neurons must be synaptically connected in several three-dimensional toy problems. (a) Cartoon depicting the 𝒩 = 3 feedforward network corresponding to the toy problems. (b), (c) Geometrically determining whether a synapse is nonzero when the target neuron responds to one input pattern but does not to two other patterns. A synapse can only vanish if the w₁ = 0 plane (orange circle) intersects the solution space (dark yellow wedge) within the weight bounds (bounding sphere). For example, this intersection occurs in panel (b), so the synapse is not required for the responses. For every synapse one can associate a direction in synaptic weight space (orange arrow) that is normal to the planes with constant synaptic weight. This synapse vector can be decomposed into its projections into the semiconstrained subspace (green arrow, $\overrightarrow{s}$) and along the constrained dimension (pink arrow, $\overrightarrow{c}$). In this example, whether the synapse is certain is determined by the size of the bounding synapse space, W [see panel (b)], the angle θ between the synapse direction (orange arrow) and the closest axis of the constrained dimension $\left(-{\overrightarrow{\epsilon }}_3\right)$ [see panel (b)], and the angle γ between $\overrightarrow{s}$ and its closest vector in the solution space $\left({\overrightarrow{s}}_{\ast }\right)$ [see panel (c)]. In panel (c), d_s depicts the perpendicular distance from the origin of the yellow semiconstrained plane in panel (b) to its intersection line with the w₁ = 0 orange plane. If this distance is sufficiently large, then the orange line will not intersect the target neuron responds to two input patterns but not the third pattern. In panel (d), the orange w₁ = 0 plane intersects the solution space (deep solution space within the yellow plane’s circular bound of radius $\tilde{W}$. (d), (e) Geometrically determining whether a synapse is nonzero when the yellow line) within the bounding sphere, so the synapse is not certain. In this example, the factors that determine synapse certainty are W [see panel (d)], the angle θ that the synapse vector (orange arrow) makes with its projection along the constrained subspace (pink arrow) [see panel (d)], and the angle α between the target response vector (brown arrow) and the pink arrow [see panel (e)]. The angle β does not ultimately matter, but it is included in the diagrams to aid the derivation. Here d_s is the distance from the brown dot to the point of intersection between the yellow line and the orange plane. Again this point will lie outside the bounding sphere if d_s is large enough, and this signals a certain synapse. (f) Geometrically determining whether a synapse is nonzero when the target neuron responds to one input pattern but does not to a second pattern. In the figure shown, the w₁ = 0 orange plane intersects the solution space (deep yellow semicircle) within the bounding sphere, so the synapse is not certain. In this example, apart from W, what determines synapse certainty are the angles θ and φ, which encode how the synapse vector (orange arrow) can be decomposed into its projections along the constrained direction (pink arrow), semiconstrained direction (green arrow) and unconstrained direction (purple arrow).