FIG. 5.

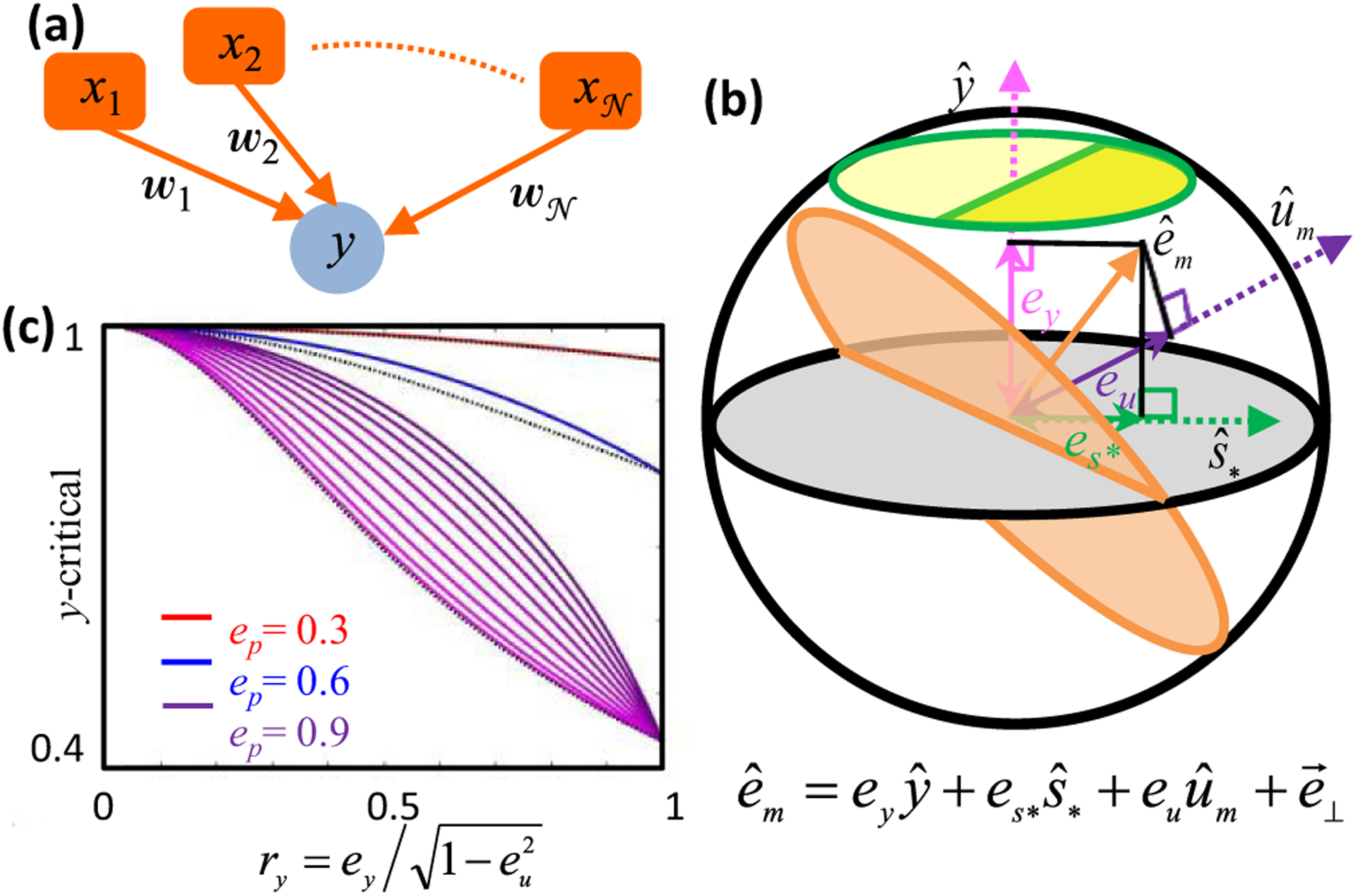
Identifying certain synapses in high-dimensional networks. (a) Cartoon depicting the high-dimensional feedforward network under consideration. (b) Geometrically determining whether a synapse is nonzero throughout a high-dimensional solution space. A synapse can only vanish if the w_m = 0 hyperplane (orange circle) intersects the solution space (dark yellow wedge) within the weight bounds (bounding sphere). In the example shown, this intersection does not occur, so the synapse must be present. For orthonormal neural responses, only a few parameters determine whether this intersection occurs (Appendix A). First, the magnitude of the weight bound, W, controls the extent of the solution space. Second, there are three projections of the synapse direction (orange arrow) whose lengths are important determinants of the certainty condition: e_y, the length of projection along the target response vector (pink arrow); e_s*, the length of projection along the closest boundary vector in the semiconstrained solution subspace [green arrow, see also ${\overrightarrow{s}}_{\ast }$ in Fig. 4(c)]; and e_u, the length of projection into the unconstrained subspace (purple arrow). Note that the shown example would have had an intersection if the solution space (dark yellow wedge) were moved down (along $\widehat{c}$) to lie below the hyperplane (orange circle). The solution space’s height is proportional to the magnitude of the postsynaptic responses, y. Thus, the solution space does not intersect the hyperplane only if y exceeds a critical value, y_cr. (c) Plots of the certainty condition, Eq. (57), for W = 1. The red, blue, and purple curves plot y_cr as a function of r_y = e_y/e_p for e_p = 0.3, 0.6, and 0.9, respectively. Different purple shades correspond to different values of $r_{s\ast }=e_{s\ast }/\sqrt{e_p^2-e_y^2}$. As this ratio increases, nonlinear effects increase y_cr and make the sign harder to determine. The red and blue curves are for the maximally nonlinear case when $r_{s\ast }=1\Rightarrow e_{s\ast }=\sqrt{e_p^2-e_y^2}$. The dashed black curves represent y_cr in a linear model, which cannot exceed the nonlinear y_cr.