FIGURE 4.

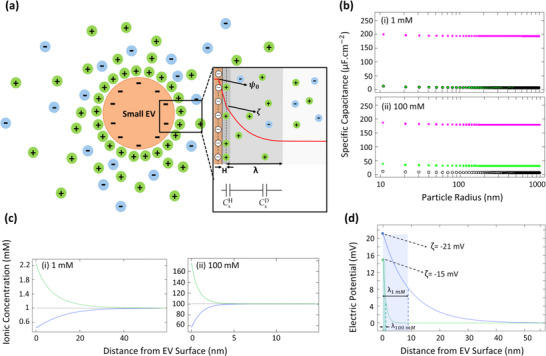
Simulated electrokinetic model for EDL around small EVs, obtained using COMSOL Multiphysics. (a) Schematic of the simulated domain according to the Gouy‐Chapman‐Stern Model; double layer structure of ions consisting of the Helmholtz layer (H) and the diffuse layer (λ). Surface potential, zeta potential, and bulk potential are denoted by ψ₀, ζ, and ${\psi }_{\infty }$, respectively. To describe the total EDL capacitance, the interfacial model was considered as two capacitances (diffuse and Helmholtz layers) combined in series; total capacitance of EDL is the sum of the individual capacitances of diffuse layer ($C_s^D$) and Helmholtz layer ($C_s^H$). (b) The predicted specific capacitance for the Helmholtz layer (pink square), diffuse layer (green square), and total EDL (black circle) of small EVs dispersed in (i) 1 mM and (ii) 100 mM electrolyte solutions based on the Gouy‐Chapman‐Stern model assuming constant permittivity (ɛ_r = 78.5) for the electrolyte solution and constant surface charge density for small EVs (identical to a ζ‐potential of −35 mV). (c) Molar concentration profile for cations and anions around small EVs dispersed in (i) 1 mM and (ii) 100 mM electrolyte solutions, representing cation accumulation (green line) and anion depletion (blue line). (d) Electric potential profile around small EVs (diameter of 100 nm, constant surface charge density, surface potential of −22 mV) dispersed in an electrolyte solution with ionic strength of 1 mM (blue line) and 100 mM (green line). Debye length (λ) is a function of electrolyte ionic strength: the higher the ionic strength, the shorter the Debye length and the smaller the magnitude of the ζ‐potential.