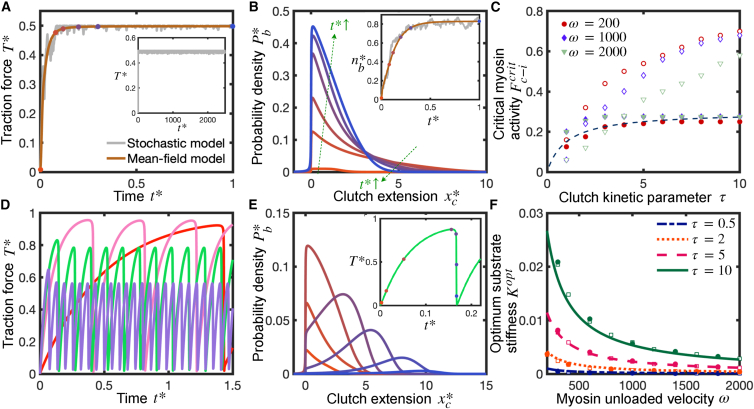
Figure 2.

Clutch-dominated protrusions produce maximum possible traction forces and do not exhibit clutch failure avalanches, whereas cellular protrusions that operate in the intermediate regime features load-and-fail dynamics and produce maximum traction forces at an intermediate substrate stiffness. Temporal evolution of the dimensionless traction force (A), probability density function (B), and fraction of bound clutches (B, inset) in a clutch-dominated protrusion. The dimensionless probability density function is obtained by the mean-field model and sampled at the time points marked by symbols in (A and B inset). Color schemes of symbols in (A and B inset) and lines in (B) correspond to the same time points. In the clutch-dominated regime, long-time traction force and fraction of bound clutches approach the total myosin stall force $\mathrm{T}={\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}$ and unloaded equilibrium fraction of bound clutches ${\mathrm{n}}_{\mathrm{b}}={\mathrm{n}}_{\mathrm{c}}{\mathrm{k}}_{\mathrm{o}\mathrm{n}}/\left({\mathrm{k}}_{\mathrm{o}\mathrm{n}}+{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}\right)$, respectively. Brown, mean-field model solution; gray, a single-trajectory of the stochastic model. (A, inset) Long-time stochastic single-trajectory. Parameter values: $\mathrm{F}=0.5,\tau =10,\omega =500,\mathrm{K}=1$. (C) Critical motor activity parameter ${\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$, which sets the border between the clutch-dominated regime and the intermediate regime, as a function of the clutch kinetic parameter $\tau$, for three values of the dimensionless myosin load-free velocity $\omega$. Protrusions with $\mathrm{F}<{\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ belong to the clutch-dominated regime and produce maximum available traction forces. Solid and open symbols correspond to the critical activity parameter in soft and rigid substrates, respectively. The dashed line is our analytical solution for soft substrates obtained via scaling analysis (Eq. 5). (D) Time evolution of dimensionless traction force for four different substrate stiffnesses: $\mathrm{K}=0.001$ (red), $\mathrm{K}=0.005$ (pink), $\mathrm{K}=0.008$ (green), and $\mathrm{K}=0.01$ (purple). Parameter values: $\mathrm{F}=1$, $\tau =10,\omega =2000$. (E) Temporal evolution of the dimensionless probability density function ${\mathrm{P}}_{\mathrm{b}}^{\ast }$ and dimensionless traction force (inset). Symbols and color scheme in inset correspond to the time points where ${\mathrm{P}}_{\mathrm{b}}^{\ast }$ is sampled. Parameter values: $\mathrm{F}=1$, $\tau =10,\omega =2000,\mathrm{K}=0.005$. (F) Dimensionless optimum substrate stiffness ${\mathrm{K}}^{\mathrm{o}\mathrm{p}\mathrm{t}}={\kappa }_{\mathrm{s}}^{\mathrm{o}\mathrm{p}\mathrm{t}}/{\mathrm{n}}_{\mathrm{c}}{\kappa }_{\mathrm{c}}$ as a function of the dimensionless myosin load-free velocity, $\omega$, for four different values of the clutch kinetic parameter $\tau$. The dimensionless clutch binding timescales as ${\mathrm{t}}_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}^{\ast }\sim 1/\left(\tau +1\right)$, whereas the dimensionless clutch rupture timescales as ${\mathrm{t}}_{\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}}^{\ast }\sim \left({\mathrm{C}}_2/\mathrm{F}+1/\mathrm{K}\omega \right)/\left(1+1/\tau \right)$. Solid lines correspond to our derived analytical solution (Eq. 6), open symbols correspond to the numerical solution of the mean-field model (Eqs. 3 and 4), and closed symbols correspond to the numerical solution of the stochastic model. Parameter value: $\mathrm{F}=2$. To see this figure in color, go online.