Figure 1.
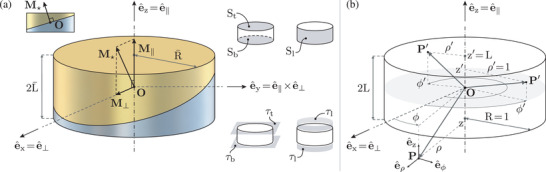
Cylindrical magnet with generic uniform magnetization. a) Magnet size (radius , half‐height ), pose (origin O, axial direction ), and magnetization (M ⋆). Magnetization, in particular, is decomposed into axial (M ∥) and diametric (M ⊥) contributions: M ⋆ = M ∥ + M ⊥. Gold/silver colors consistently remind of magnetic poles. b) Non‐dimensional cylindrical coordinates: illustration for two generic points P′ on the surface of the magnet, and a generic point P outside the magnet. The unit vectors systems and represent the considered cylindrical and intrinsic (Cartesian) frames, respectively. We obtained exact and computationally robust analytical solutions, for both magnetic field and field gradient, at generic points P outside or inside the magnet (and, by superposition, our solutions extend to cylindrical magnets systems of arbitrary complexity, in terms of both spatial arrangement and magnetization pattern).
