Figure 9.

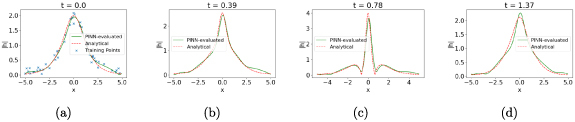
The PINN-evaluated $|h(x,t)|$ at different timeslices, $t=0,0.39,0.78,1.37$, from left to right. In this case the PINN is constained by the Schrodinger equations first conservation law: $\frac{d}{\mathrm{d}t}\int |h{|}^2\mathrm{d}x=0$. The training data on the initial timeslice is subject to measurement errors, modeled by a Gaussian random variable with zero mean and a standard deviation of σ = 0.1. The points marked with the blue cross (x) pointer in the leftmost set of plots indicate the samples on the initial timeslice used to train the PINN.