Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Aug 21;95(35):13227–13234. doi: 10.1021/acs.analchem.3c02298

Broadband Two-Photon Absorption Spectroscopy with Stimulated Raman Scattering as an Internal Standard

Prasenjit Srivastava 1, David A Stierwalt 1, Christopher G Elles 1,*
PMCID: PMC10484208  PMID: 37603818

Abstract

graphic file with name ac3c02298_0008.jpg

Two-photon absorption (2PA) spectroscopy provides valuable information about the nonlinear properties of molecules. In contrast with single-wavelength methods, broadband 2PA spectroscopy using a pump–probe approach gives a continuous 2PA spectrum across a wide range of transition energies without tuning the excitation laser. This contribution shows how stimulated Raman scattering from the solvent can be used as a convenient and robust internal standard for obtaining accurate absolute 2PA cross sections using the broadband approach. Stimulated Raman scattering has the same pump–probe overlap dependence as 2PA, thus eliminating the need to measure the intensity-dependent overlap of the pump and probe directly. Eliminating the overlap represents an important improvement because intensity profiles are typically the largest source of uncertainty in the measurement of absolute 2PA cross sections using any method. Raman scattering cross sections are a fundamental property of the solvent and therefore provide a universal standard that can be applied any time the 2PA and Raman signals are present within the same probe wavelength range. We demonstrate this approach using sample solutions of coumarin 153 in methanol, DMSO, and toluene, as well as fluorescein in water.

Introduction

The two-photon absorption (2PA) process plays an important role in applications ranging from fluorescence imaging and photodynamic therapy to 3D data storage.1−6 A characteristic property of 2PA is the requirement for high-intensity irradiation in order to achieve the simultaneous absorption of two photons that are individually non-resonant with the target molecule. In the case of two-photon microscopy, for example, this criterion eliminates out-of-focus excitation of a fluorescent dye, where the intensity is too low to induce two-photon absorption and therefore results in highly localized excitation that can exceed the diffraction limit.7,8 Two-photon absorption has the added benefit of using longer-wavelength photons to achieve the same total excitation energy compared with linear absorption, which typically results in deeper penetration of the sample (i.e., for deep tissue imaging) and eliminates the need for damaging UV irradiation.9,10

The promise of harnessing 2PA for various applications has inspired intense effort to develop novel chromophores with large 2PA cross-sections, σ2PA.11 However, developing new two-photon chromophores is often limited by the difficulty of measuring accurate cross sections across a wide range of the spectrum using single-wavelength techniques. The most common methods for measuring two-photon absorption cross-sections include z-scan and two-photon excited fluorescence (2PEF).12,13 Both of these approaches measure the degenerate 2PA cross-section, where two photons are absorbed from a single laser beam and therefore share the same wavelength and polarization properties. For example, open-aperture z-scan measurements involve the translation of a sample along the propagation axis (i.e., the z axis) of a focused laser beam. Attenuation of the transmitted laser intensity varies as the sample moves through the laser focus, with the maximum attenuation occurring at the focal point, where the highest intensity results in the strongest two-photon absorption.14,15 The other commonly used technique is two-photon excited fluorescence (2PEF), in which the fluorescence intensity of a target molecule is used as a measure of the relative two-photon absorption strength.16 The 2PEF approach does not directly measure two-photon absorption but rather relies on independent knowledge of the fluorescence quantum yield of the target molecule, which is generally assumed to be the same for one- and two-photon excitation.

An important limitation of the monochromatic z-scan and 2PEF techniques is the need to tune the laser in order to acquire the full 2PA spectrum. Tuning the wavelength often results in variation of the spatial profile of the laser beam, which can lead to artifacts in the 2PA spectrum. Determining the absolute cross section requires precise knowledge of the intensity profile of the excitation laser passing through the sample; therefore, any irregularity in the temporal pulse profile or hot spots in the spatial beam profile can lead to a systematic error in the determination of σ2PA due to the intensity-dependence of the 2PA signal. This intensity dependence may explain the wide variability in reported values for σ2PA even though several 2PA reference standards are now available for calibration.12,17−19 A z-scan technique using spatially dispersed, high-intensity broadband continuum laser pulses was developed in order to avoid tuning the laser wavelength by measuring the continuous 2PA spectrum directly.20−22 However, the dispersed z-scan approach does not readily provide absolute cross sections and has not been widely adopted.

An alternative approach for measuring 2PA spectra without tuning the laser wavelength uses pump–probe spectroscopy with individually non-resonant pump and probe light.23−25 The broadband pump–probe method measures the non-degenerate 2PA spectrum as a function of the combined pump and probe photon energies based on the wavelength-dependent attenuation of white-light probe pulses in the presence of more intense single-wavelength pump pulses. Broadband 2PA (BB-2PA) spectroscopy uses a typical pump–probe configuration, except that the pump wavelength is not individually resonant with an allowed transition of the molecule. Thus, the 2PA signal is only observed when the pump and probe pulses are temporally coincident on the sample, resulting in the simultaneous absorption of one pump and one probe photon. The broadband probe measures the continuous 2PA spectrum and eliminates the need for single-point measurements as in the z-scan and 2PEF methods. Importantly, broadband 2PA spectroscopy measures the two-photon absorption strength directly and, therefore, is independent of the fluorescence quantum yield, while also providing the flexibility to independently tune the wavelength and relative polarization of the pump and probe photons.

Determining accurate 2PA cross-sections using the broadband pump–probe approach requires precise knowledge of the intensity-dependent overlap of the pump and probe pulses in the sample.26 In this contribution, we show that stimulated Raman scattering (SRS) from the solvent provides a convenient and robust internal standard for the accurate measurement of absolute 2PA cross-sections. Importantly, the SRS and 2PA signals have the same pump–probe overlap dependence and can be measured simultaneously when the Raman scattering signal falls within the range of measured probe wavelengths. The SRS signal is a fundamental property of the solvent and therefore provides an internal standard that can be used to compensate for any variation of the pump–probe overlap compared with the measured beam profiles. In fact, the SRS signal completely eliminates the need to measure the pump–probe overlap, providing a substantial improvement in the accuracy of the measured 2PA cross section. Furthermore, the absolute value of σ2PA can be easily corrected at any time if a more accurate value of the solvent Raman cross section becomes available.

This contribution demonstrates the use of Raman cross sections as an internal standard for broadband 2PA spectroscopy using coumarin 153 (C153) as an example. C153 is a common laser dye that has been used as a reference standard in 2PA spectroscopy.12 We report the 2PA spectrum of C153 in three different solvents for which the Raman scattering cross sections were measured previously.27 We compare our broadband results with previously reported cross sections and 2PA spectra that were obtained using 2PEF. This approach is completely general and could be applied to any two-photon absorbing chromophore in a solvent for which the Raman cross section is known.

Experimental Details

We measure broadband 2PA spectra using a pump–probe method, as described previously.23,25,28,29 Briefly, we use nonlinear frequency conversion to obtain the tunable pump and probe pulses from the output of an amplified Ti:Sapphire laser (Coherent, Legend Elite) operating at 1 kHz. One optical parametric amplifier (OPA) produces pump pulses at 1158 nm (1.07 eV), and we focus the 1200 nm output from a second OPA into a circularly translating 1 mm CaF2 substrate to obtain broadband probe pulses via white-light continuum generation. A pair of parabolic aluminum mirrors collimates and then focuses the broadband probe to a diameter of approximately 100 μm at the sample, after which a transmission grating disperses the probe light onto a 256-element photodiode array for broadband detection. The probe covers a spectral range of 500–1000 nm (1.24–2.48 eV), and we use cut-off filters to prevent second-order dispersion of shorter-wavelength light from reaching the detector. A synchronized chopper wheel blocks alternating pump pulses for active background subtraction.

The pump and probe beams cross at a small angle of less than 10° in the sample, which consists of a 13 mM solution of coumarin 153 (Sigma, 99%) in methanol, DMSO, or toluene in a 1 cm quartz cuvette. We use a variable neutral density filter to attenuate the pump energy (typically 1 μJ per pulse) and adjust the spot size at the sample in order to eliminate transient absorption signals due to degenerate non-linear excitation by the pump pulse. The time-dependent absorption signal is measured by scanning the delay (τ) between the pump and probe pulses to measure both the 2PA and SRS signals simultaneously. Scanning a small range of time delays is necessary to record the 2PA and SRS signals over the full range of pump–probe overlap and to account for the group velocity dispersion of the broadband probe pulse. We record 2000 laser shots per time delay and average 3 separate scans for each spectrum. We measured the stimulated Raman spectra of the neat solvents using exactly the same conditions as the 2PA spectra. For comparison, we also measure SRS spectra using narrower-bandwidth picosecond pump pulses and a higher-resolution spectrograph in order to better resolve the individual Raman bands.27 The narrow bandwidth picosecond pump pulses were generated using spectral compression via second harmonic generation (SC-SHG) in a long β-barium borate (BBO) crystal followed by a 4f spatial filter.30

Results and Analysis

Broadband 2PA Spectroscopy

The contour plot in Figure 1 shows the broadband pump–probe spectrum of C153 in methanol as a function of time delay and probe wavelength. The absorption signal in the 2D image, ΔA(τ,λprobe), includes contributions from both absorptive and dispersive interactions between the pump and probe pulses. The signals are only present when the pump and probe are temporally coincident because each pulse individually is non-resonant with the sample. The temporal chirp of the broadband probe due to group velocity dispersion is evident from the curved shape of the signal, which causes different wavelengths of probe light to overlap with the pump pulse at slightly different delay times. The solid line in the image tracks the point of maximum pump–probe overlap, for which a positive signal represents the simultaneous absorption of one pump and one probe photon. In addition to the 2PA signal, a localized region of positive absorption due to stimulated Raman scattering (SRS) is evident near 870 nm, and a pair of positive and negative bands due to cross-phase modulation (XPM) are present near the 1000 nm probe wavelength.

Figure 1.

Figure 1

Open in a new tab

Top: pump–probe absorption signal for C153 in methanol. The solid line shows the maximum pump–probe overlap, and dashed lines illustrate increasing limits of integration. Bottom: integrated signal for increasing integration range.

Integrating the absorption signal over the full range of time delays for which the pump and probe interact at a given wavelength eliminates dispersive features caused by XPM while retaining absorptive and emissive features, including 2PA and SRS.31,32 In the weak interaction limit, the positive and negative features from XPM are equally balanced, whereas absorptive (or emissive) interactions result in the net loss (or gain) of a photon in the probe beam and therefore contribute a positive (or negative) signal in the integrated spectrum. We vary the integration range to ensure complete integration of the pump–probe interaction at each wavelength, as illustrated by the dashed lines in the contour plot. The lower panel of Figure 1 shows the integrated signal, ΔA(λprobe) = ∫ΔA(τ,λprobe)dτ, as a function of increasing integration range. Notably, negative signals due to XPM are entirely eliminated, and the signal remains constant when the integration range exceeds the pump–probe interaction time, confirming that there is no transient absorption signal induced by the pump pulse.

The integrated signal includes contributions from both 2PA and stimulated Raman scattering. In order to distinguish the two contributions, we also measure the spectrum of the pure solvent, for which there is no 2PA but SRS remains (see Figure 2). The magnitude of the solvent Raman scattering signal is significantly larger than that of the solute because of the 3 orders of magnitude larger number density of the solvent; therefore, the Raman signal in the 800–900 nm range of probe wavelengths is essentially the same for the pure solvent and the solution of C153. Both SRS and 2PA signals vary linearly with pump and probe intensity, confirming that there is no competition between the two processes and that this is indeed the weak interaction limit.

Figure 2.

Figure 2

Open in a new tab

Integrated absorption signal for the solution of C153 in methanol and for pure methanol. Contributions from solute 2PA and solvent SRS are indicated. The dark blue line is the SRS signal for pure methanol at higher resolution.

The solute 2PA and solvent SRS signals are a result of different interactions between the pump and probe fields in the sample, but both signals contribute within the same range of probe wavelengths. The different probe wavelength dependences of each signal are illustrated by the split axis at the top of Figure 2. One portion of the split axis shows the pump–probe frequency difference, or Raman shift (in cm–1), for the SRS signal; the other portion shows the total combined energy of the pump and probe photons (in eV) for the 2PA signal. The resolution of SRS scattering signals is limited by the ∼250 cm–1 bandwidth of the <80 fs pump pulses. For comparison, Figure 2 also shows the Raman spectrum that we obtain using picosecond pump pulses with 10 cm–1 bandwidth in order to resolve the individual C–H and O–H bands of methanol. We showed previously that the frequency-integrated intensity of an SRS band is independent of the spectral resolution.27

Here, we observe SRS as a Raman loss signal, for which the probe is higher in frequency than the 1158 nm pump light (i.e., on the anti-Stokes side).33 The Raman loss process is analogous to Raman gain except that the roles of pump and probe are reversed.34,35 The schematic energy level diagram in Figure 3 illustrates this difference, with the broadband probe light acting as the Raman excitation field and the 1158 nm pump pulse acting as the stimulated Raman field. The net result is a loss of intensity in the probe field (i.e., a positive signal in the TA spectrum) and a concomitant gain of intensity in the pump field (which we do not measure). Raman gain and Raman loss intensities are only different by the sign;36−39 therefore, the SRS signal strength is directly related to the spontaneous Raman scattering cross section in each case, as described below.

Figure 3.

Figure 3

Open in a new tab

Schematic energy–level diagrams for non-degenerate 2PA and SRS. Red arrows represent the 1158 nm pump pulse, and multi-colored arrows represent the broadband probe pulse.

Subtracting the solvent-only signal effectively eliminates the SRS contribution from the spectrum of the sample, leaving only the 2PA spectrum of the solute. Figure 4 illustrates this approach for solutions of C153 in methanol, DMSO, and toluene. The figure shows the 2PA spectra plotted as a function of the transition wavelength, which is equivalent to the wavelength of light that would be required to access the same total energy using a single photon. The top axis of the figure shows the total energy in eV, where the full range is determined by the combined energy of the pump (1.08 eV) and probe photons (1.24–2.48 eV).

Figure 4.

Figure 4

Open in a new tab

Broadband 2PA spectrum of C153 in methanol, DMSO, and toluene. In each case, the SRS spectrum of the pure solvent (blue line) is subtracted from the integrated signal of the solution (red line) to obtain the solute 2PA spectrum (green line).

Absolute Cross Sections

The broadband 2PA spectrum that we obtain using the pump–probe method provides the relative transition strength as a function of the total energy of pump and probe photons, εtotal. The absolute 2PA cross-section at a given transition energy in units of GM (1 GM = 10–50 cm4·s·molec.–1·photon–1) is proportional to the time-integrated transient absorption signal at the corresponding probe wavelength

graphic file with name ac3c02298_m001.jpg 1

where NA is Avogadro’s number, ωpump is the angular frequency of the pump light (rad/s), Epump is the energy of the pump pulses (J/pulse), csolute is the concentration of the solute (mol/L), fV is the intensity-weighted spatial overlap (cm–1) of the pump and probe beams passing through the sample, and the time-integrated two-photon absorption signal ΔA2PA has units of mOD·s. The overlap between the pump and probe beams is the most significant source of uncertainty in the calculation of the absolute 2PA cross-section from the transient absorption signal. Although the overlap factor, fV, can be estimated from the relative beam diameters,40 the actual overlap is sensitive to irregularities in the spatial beam profiles as well as the crossing angle and focal conditions of the pump and probe beams passing through the sample. To overcome this limitation, we use the SRS signal from the solvent as an internal standard to calibrate the pump–probe overlap.

The SRS signal at Raman scattering frequency ωRaman has the same overlap dependence as the 2PA signal

graphic file with name ac3c02298_m002.jpg 2

where csolvent is now the concentration of the solvent (mol/L), and ΔASRS is the integrated absorption signal due to stimulated Raman scattering of the solvent at the corresponding probe wavelength (mOD·s). The other parameters are exactly the same as in the 2PA measurement; therefore, we use the SRS signal and the (known) Raman scattering cross section of the solvent to avoid using fV directly in the determination of σ2PA.

The frequency-dependent SRS cross section, σSRS(ωRaman), has units of GM, just like the 2PA cross section.41 However, the SRS signal is also directly related to traditional spontaneous Raman cross sections, which have been more widely reported. The SRS cross section is related to the differential cross section for spontaneous Raman scattering of linearly polarized light

graphic file with name ac3c02298_m003.jpg 3

where we take the integral over the full Raman band to account for the limited spectral resolution using femtosecond (or picosecond) laser pulses and to simplify the comparison with previously published Raman cross sections.27 In the equation, Ω is the solid angle, c is the speed of light, n is the index of refraction of the solvent, and ω2 is the lower-frequency component in the SRS process (ωprobe for Raman gain and ωpump for Raman loss). The term involving ω22 comes from the comparison with spontaneous scattering, which incorporates the blackbody field at the lower frequency.42,43 There is no angular dependence in stimulated Raman scattering because the SRS signal is phase-matched to the probe pulse.44

Combining the equations for 2PA and SRS cross sections and taking the integral over the full Raman band of the solvent gives the 2PA spectrum of the solute

graphic file with name ac3c02298_m004.jpg 4

relative to the band-integrated Raman signal of the pure solvent. The subscript RL indicates that the cross section is for Raman loss scattering with 1158 nm pump light, and we integrate the SRS band over the angular frequency (rather than wavelength) of the probe light in order to match the convention for spontaneous Raman cross sections (i.e., eq 3). In the case of methanol, we integrate over both the O–H and C–H Raman bands (roughly 2500–4000 cm–1) due to the low resolution of the SRS spectrum when using femtosecond laser pulses. The combined C–H/O–H cross section, for methanol and the cross sections for the C–H bands of DMSO and toluene are listed in Table 1 (see also Figure S1 in the Supporting Information). We recently reported Raman cross sections for several solvents (including methanol, DMSO, and toluene) and also confirmed that the time- and frequency-integrated values of σSRS are independent from the pulse duration as long as the absorption signal is integrated over the full bandwidth and the full range of delay times for which the pump and probe are overlapped.27

Table 1. Absolute Cross Sections for Solvent SRS and Solute 2PA.

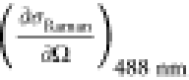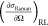sample Inline graphica (10–30 cm2 sr.–1 molec.–1) Inline graphicb (10–30 cm2 sr.–1 molec.–1) λmaxc (nm) σ2PA(λmax) (GM)
C153/methanol 10.5 0.72 424 58.6
C153/DMSO 23.7 1.62 427 72.8
C153/toluene 38.1 2.60 408 69.4
fluorescein/waterd 4.4 0.47 390 69.5
fluorescein/waterd 4.4 0.47 455 16.2
Open in a new tab
a

C–H/O–H for methanol, C–H for DMSO and toluene, and O–H for water. From ref (27).

c

Transition wavelength at 2PA band maximum.

d

Measured at 1030 nm, see Supporting Information.

The previously reported cross sections were obtained using stimulated Raman gain spectroscopy with an excitation wavelength of 488 nm. In order to account for the wavelength dependence of the Raman cross section in the absence of resonance enhancement effects, we apply a frequency correction factor

graphic file with name ac3c02298_m005.jpg 5

where ω1 and ω2 are the higher and lower frequency fields in the 488 nm reference measurement, respectively, and ω1′ and ω2 are the higher and lower frequencies from the SRS signal measured here, respectively. When measuring Raman loss spectra, the roles of the pump and probe fields are reversed compared with Raman gain scattering; therefore, ω1′ is the probe frequency, and ω2 is the pump frequency. The low-frequency term is always cubed because it comes from the comparison with spontaneous Raman scattering.42,43,45 Although the probe frequency spans a small range, we take ωprobe as the center frequency of the observed Raman band. Neglecting resonance enhancement effects is reasonable for solvents that have a large optical band gap, but we note that the actual SRS cross sections may be slightly smaller than predicted by this simple frequency correction.46

Using the Raman signal as an internal standard gives the full broadband 2PA spectrum of C153 on an absolute scale (i.e., in units of GM), as in Figure 5. The figure also shows previously reported 2PA spectra and absolute cross sections from single-wavelength measurements of C153 in all three solvents. In the case of DMSO and toluene, degenerate cross sections were reported across the full 2PA band by tuning the laser wavelength.12 For comparison, the figure also shows the 1PA spectrum of C153 in each solvent. Note that we use the transition wavelength in order to facilitate the comparison between the 1PA and 2PA spectra. Table 1 lists the values of σ2PA at the maximum of the 2PA band in each solvent.

Figure 5.

Figure 5

Open in a new tab

Absolute 2PA spectrum of C153 in methanol, DMSO, and toluene. Red lines are the solvent-calibrated broadband 2PA spectra from this work, markers show previously reported values from single-wavelength measurements,12,47 and green lines are the 1PA spectra.

We demonstrate the versatility of this approach by also measuring the 2PA spectrum of fluorescein in water (Figure S2). Fluorescein is another common 2PA standard and has two distinct absorption bands in the visible region of the spectrum. In the case of the fluorescein measurement, we use a 1030 nm excitation wavelength with slightly higher frequency resolution in order to distinguish CH and OH bands in the SRS spectrum. Only the OH bands of water contribute to the integrated absorption spectrum of the sample, confirming that the solute SRS bands are insignificant compared with the solvent due to the much higher concentration of the latter. The fluorescein measurement also demonstrates that the solvent SRS bands can be completely removed from the 2PA spectrum by subtracting the solvent-only signal, even when the SRS bands fall directly on top of a 2PA band. We report absolute 2PA cross sections for both of the absorption bands of fluorescein in Table 1.

Discussion

Comparison with Other Measurements

The broadband 2PA (BB-2PA) spectra that we measure for C153 in DMSO and toluene closely match the spectral shapes of the degenerate 2PA spectra reported by de Reguardati et al.12 using the 2PEF method (see Figure 5). Reported values for 2PA cross sections often vary by an order of magnitude or more between measurements;18 therefore, our absolute cross sections are in good agreement with the single-wavelength values, including the single-point measurement in methanol by Melnikov et al.47 In principle, our approach using stimulated Raman scattering of the solvent as an internal standard gives very accurate values of σ2PA(εtotal) and is only limited by the quality of the Raman cross section used for calibration. Raman cross sections are a fundamental property of the solvent and therefore have the potential to be known very precisely and will not vary from one measurement to another. Furthermore, the calibrated 2PA cross section of a solute can be easily updated if more accurate Raman cross sections become available at a later date, an option that is not possible for traditional 2PA methods, where the determination of absolute cross sections is entirely dependent on experimental parameters, including the spatial and temporal beam profiles. While several dye molecules have been proposed as external standards for comparison with newly measured 2PA spectra, a similar approach can also be used with BB-2PA for reassurance.

One important point is that the broadband 2PA measurement provides non-degenerate 2PA cross sections, compared with the degenerate cross sections from single-wavelength measurements.48 Although resonance-enhancement effects might lead to slightly different cross sections for degenerate and non-degenerate excitation at the same total energy, we anticipate only minor differences for the range of wavelengths that are used here. The similar spectral shapes for the BB-2PA and 2PEF measurements in Figure 5 confirm that at least there are not dramatic variations in the 2PA intensity as the pump and probe wavelengths increasingly diverge across the spectrum. The role of resonance enhancement in non-degenerate 2PA cross sections is an interesting topic that deserves further exploration.28,40 In any case, we note that the pump–probe approach measures 2PA directly, unlike 2PEF, which depends on knowing the (potentially wavelength-dependent) fluorescence quantum yield of the target molecule. The non-degenerate measurement also allows us to tune the properties of the pump and probe independently, including the relative polarization of the two photons.

The broadband 2PA technique accurately reproduces a solvatochromic shift of the absorption band that is apparent from the 1PA spectra for C153 (see Figure 6). The solvent shifting of the 2PA band in C153 highlights the value of a broadband measurement compared with single-wavelength methods. In the case of C153, the 1PA and 2PA bands closely match, but other molecules often have shifted absorption bands due to different Franck–Condon factors for one- and two-photon transitions, or even different spectra altogether due to symmetry selection rules, either of which would preclude comparisons like we have made in Figures 5 and 6.49,50 In addition to the solvatochromic shift, the broadband method reveals an asymmetric absorption band for C153 in toluene that mirrors the 1PA spectrum. While a similar change in the band shape is evident from the 2PEF measurements, single-wavelength approaches are very sensitive to variation of the intensity profile when tuning the excitation laser across the absorption band, which can lead to systematic variation that is difficult to diagnose when the 1PA and 2PA bands are not identical.

Figure 6.

Figure 6

Open in a new tab

One- and two-photon absorption spectra for C153 in methanol, DMSO, and toluene.

The broadband approach is not entirely immune from similar variation of the intensity profile with excitation energy because the measurement depends on uniform overlap between pump and probe beams across the entire spectral range of the probe pulse. While there is a possibility of different overlap across the spectrum of the broadband probe, we counter this effect by using a relatively large pump beam at the sample (generally 2–3 times larger than the probe) and also comparing the 2PA signals for many independent measurements to ensure that the spectrum is not distorted. The pump–probe overlap is easy to check by varying the beam parameters between repeated measurements, by comparison with a known 2PA standard, or with the transient absorption signal from a traditional pump–probe measurement using resonant excitation.

Generality of the Approach

The broadband 2PA measurement is easily applied to any two-photon absorbing chromophore for which an absorption band is accessible within the range of available pump and probe photons. Using the SRS signal of the solvent for internal calibration of the absolute cross section is similarly general, provided one or more Raman bands from the solvent are accessible in the same range of probe wavelengths. While we have demonstrated this approach using Raman loss scattering with 1158 nm pump pulses, we have also achieved similar results using Raman gain scattering signals from higher energy (shorter wavelength) pump pulses. The equations provided above are intentionally generic so that they may be used for either stimulated Raman gain or loss. Spontaneous Raman cross sections have been reported for many solvents51−54 or can be measured using the same pump–probe approach that we use for the broadband 2PA measurements (provided beam overlap conditions can be determined).27

The broadband measurements presented here use pump and probe beams that overlap in a 1 cm cuvette with a small crossing angle. We note that the relatively long path length compared with typical ultrafast pump–probe measurements is advantageous because the crossing beams do not interact at the sample windows, thus reducing the magnitude of the XPM signal.31 Interactions at the sample windows in shorter path length cells give larger XPM signals that result in residual error in the integrated spectrum. On the other hand, the reduced time resolution compared with shorter sample cells is not a concern here because the time-integrated signal is independent of walk-off and dispersion. We also point out that the use of an internal standard for calibration of the absolute cross section is independent of sample path length and therefore may also be suitable for solid-state samples.

Finally, we note that although the measurements presented here were all done with parallel relative polarization of the pump and probe in order to facilitate the comparison with single-beam measurements, the pump–probe approach easily enables polarization-dependent measurements.55 For example, stimulated Raman cross sections for perpendicular polarization are easily obtained from spontaneous cross sections having the same polarization dependence or from the cross section at parallel polarization and the depolarization ratio.27 In cases where both parallel and perpendicular polarization are measured, the depolarization ratio of the solvent Raman band provides a simple measure of the polarization purity for the 2PA spectrum.

Conclusions

Stimulated Raman scattering from the solvent provides a convenient and reliable internal standard for determining accurate cross sections using the broadband pump–probe approach to 2PA spectroscopy. Using the Raman signal as an internal standard eliminates the need to measure the pump–probe overlap directly, thereby removing the primary source of uncertainty in determining absolute 2PA cross sections. This approach is easily implemented and provides broadband spectra in a fraction of the time necessary for single-wavelength measurements such as z-scan or 2PEF.

The approach is very general because any Raman-active vibration can be used as an internal standard, including the OH stretch of water, as we have shown in Figure S2 of the Supporting Information. In fact, we previously published absolute Raman cross sections for 7 different solvents (including water),27 which highlights the versatility of using solvent SRS bands as an internal standard. Furthermore, our proof-of-principle measurements in this manuscript show that the Raman bands can be adequately subtracted from the 2PA signal, so the overlapping signals are not a problem.

The absolute 2PA cross-sections that we obtain for C153 in methanol, DMSO, and toluene are in good agreement with values previously reported in the literature. The broadband 2PA technique also resolves solvatochromic shifts of the C153 spectrum as well as small changes in the shape of the absorption band due to solvent interactions. Using SRS cross sections of the solvent as an internal standard therefore makes the broadband approach an especially valuable tool for accurate determination of 2PA spectra that will help accelerate the development of new two-photon chromophores by providing accurate cross sections using routine broadband pump–probe methods that are already widely available.

Acknowledgments

This material is based upon work supported by the National Science Foundation under grant no. CHE-1905334.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.analchem.3c02298.

  • Brief description of the relationships between energy, wavelength, and frequency for broadband 2PA and SRS measurements; higher-resolution solvent SRS spectra; and 2PA spectrum of fluorescein in water (PDF)

The authors declare no competing financial interest.

Supplementary Material

ac3c02298_si_001.pdf (865.2KB, pdf)

References

  1. Bonney S. K.; Sullivan L. T.; Cherry T. J.; Daneman R.; Shih A. Y. Distinct features of brain perivascular fibroblasts and mural cells revealed by in vivo two-photon imaging. J. Cereb. Blood Flow Metab. 2022, 42, 966–978. 10.1177/0271678X211068528. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Zhai B.; Hu W.; Zhai S.; Liang T.; Liu Z. Two-photon imaging for visualizing polarity in lipid droplets during chemotherapy induced Ferroptosis. Talanta 2023, 256, 124304. 10.1016/j.talanta.2023.124304. [DOI] [PubMed] [Google Scholar]
  3. Kailass K.; Sadovski O.; Zipfel W. R.; Beharry A. A. Two-Photon Photodynamic Therapy Targeting Cancers with Low Carboxylesterase 2 Activity Guided by Ratiometric Fluorescence. J. Med. Chem. 2022, 65, 8855–8868. 10.1021/acs.jmedchem.1c01965. [DOI] [PubMed] [Google Scholar]
  4. Wei X.; Cui W. B.; Qin G. Y.; Zhang X. E.; Sun F. Y.; Li H.; Guo J. F.; Ren A. M. Theoretical Investigation of Ru(II) Complexes with Long Lifetime and a Large Two-Photon Absorption Cross-Section in Photodynamic Therapy. J. Med. Chem. 2023, 66, 4167–4178. 10.1021/acs.jmedchem.3c00047. [DOI] [PubMed] [Google Scholar]
  5. Mikulchyk T.; Oubaha M.; Kaworek A.; Duffy B.; Lunzer M.; Ovsianikov A.; E-Gul S.; Naydenova I.; Cody D. Synthesis of Fast Curing, Water-Resistant and Photopolymerizable Glass for Recording of Holographic Structures by One- and Two-Photon Lithography. Adv. Opt. Mater. 2022, 10, 2102089. 10.1002/adom.202102089. [DOI] [Google Scholar]
  6. Iliopoulos K.; Krupka O.; Gindre D.; Sallé M. Reversible two-photon optical data storage in coumarin-based copolymers. J. Am. Chem. Soc. 2010, 132, 14343–14345. 10.1021/ja1047285. [DOI] [PubMed] [Google Scholar]
  7. So P. T. C.; Dong C. Y.; Masters B. R.; Berland K. M. Two-Photon Excitation Fluorescence Microscopy. Annu. Rev. Biomed. Eng. 2000, 2, 399–429. 10.1146/annurev.bioeng.2.1.399. [DOI] [PubMed] [Google Scholar]
  8. Varnavski O.; Gunthardt C.; Rehman A.; Luker G. D.; Goodson T. Quantum Light-Enhanced Two-Photon Imaging of Breast Cancer Cells. J. Phys. Chem. Lett. 2022, 13, 2772–2781. 10.1021/acs.jpclett.2c00695. [DOI] [PubMed] [Google Scholar]
  9. Bolze F.; Jenni S.; Sour A.; Heitz V. Molecular photosensitisers for two-photon photodynamic therapy. Chem. Commun. 2017, 53, 12857–12877. 10.1039/c7cc06133a. [DOI] [PubMed] [Google Scholar]
  10. Denk W.; Strickler J.; Webb W. Two-photon laser scanning fluorescence microscopy. Science 1990, 248, 73–76. 10.1126/science.2321027. [DOI] [PubMed] [Google Scholar]
  11. Pawlicki M.; Collins H. A.; Denning R. G.; Anderson H. L. Two-photon absorption and the design of two-photon dyes. Angew. Chem., Int. Ed. 2009, 48, 3244–3266. 10.1002/anie.200805257. [DOI] [PubMed] [Google Scholar]
  12. de Reguardati S.; Pahapill J.; Mikhailov A.; Stepanenko Y.; Rebane A. High-accuracy reference standards for two-photon absorption in the 680–1050 nm wavelength range. Opt. Express 2016, 24, 9053. 10.1364/oe.24.009053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Araújo R. S.; Sciuti L. F.; Cocca L. H.; Lopes T. O.; Silva A. A.; Abegão L. M.; Valle M. S.; Rodrigues J. J.; Mendonça C. R.; De Boni L.; Alencar M. A. Comparing two-photon absorption of chalcone, dibenzylideneacetone and thiosemicarbazone derivatives. Opt. Mater. 2023, 137, 113510. 10.1016/j.optmat.2023.113510. [DOI] [Google Scholar]
  14. Yin M.; Li H. P.; Tang S. H.; Ji W. Determination of nonlinear absorption and refraction by single Z-scan method. Appl. Phys. B: Lasers Opt. 2000, 70, 587–591. 10.1007/s003400050866. [DOI] [Google Scholar]
  15. Bridges R. E.; Fischer G. L.; Boyd R. W. Z-scan measurement technique for non-Gaussian beams and arbitrary sample thicknesses. Opt. Lett. 1995, 20, 1821. 10.1364/ol.20.001821. [DOI] [PubMed] [Google Scholar]
  16. Hermann J. P.; Ducuing J. Absolute measurement of two-photon cross sections. Phys. Rev. A: At., Mol., Opt. Phys. 1972, 5, 2557–2568. 10.1103/physreva.5.2557. [DOI] [Google Scholar]
  17. Velasco M. G. M.; Allgeyer E. S.; Yuan P.; Grutzendler J.; Bewersdorf J. Absolute two-photon excitation spectra of red and far-red fluorescent probes. Opt. Lett. 2015, 40, 4915. 10.1364/ol.40.004915. [DOI] [PubMed] [Google Scholar]
  18. Makarov N. S.; Drobizhev M.; Rebane A. Two-photon absorption standards in the 550-1600 nm excitation wavelength range. Opt. Express 2008, 16, 4029–4047. 10.1364/oe.16.004029. [DOI] [PubMed] [Google Scholar]
  19. Schafer K. J.; Hales J. M.; Balu M.; Belfield K. D.; Van Stryland E. W.; Hagan D. J. Two-photon absorption cross-sections of common photoinitiators. J. Photochem. Photobiol., A 2004, 162, 497–502. 10.1016/s1010-6030(03)00394-0. [DOI] [Google Scholar]
  20. Balu M.; Hales J.; Hagan D. J.; Van Stryland E. W. White-light continuum Z-scan technique for nonlinear materials characterization. Opt. Express 2004, 12, 3820–3826. 10.1364/opex.12.003820. [DOI] [PubMed] [Google Scholar]
  21. De Boni L.; Andrade A. A.; Misoguti L.; Mendonca C. R.; Zilio S. C. Z-scan measurements using femtosecond continuum generation. Opt. Express 2004, 12, 3921. 10.1364/opex.12.003921. [DOI] [PubMed] [Google Scholar]
  22. He G.; Lin T.-C.; Prasad P.; Kannan R.; Vaia R.; Tan L.-S. New technique for degenerate two-photon absorption spectral measurements using femtosecond continuum generation. Opt. Express 2002, 10, 566. 10.1364/oe.10.000566. [DOI] [PubMed] [Google Scholar]
  23. Negres R. A.; Hales J. M.; Kobyakov A.; Hagan D. J.; Van Stryland E. W. Experiment and analysis of two-photon absorption spectroscopy using a white-light continuum probe. IEEE J. Quantum Electron. 2002, 38, 1205–1216. 10.1109/jqe.2002.802448. [DOI] [Google Scholar]
  24. Negres R. a.; Hales J. M.; Kobyakov A.; Hagan D. J.; Van Stryland E. W. Two-photon spectroscopy and analysis with a white-light continuum probe. Opt. Lett. 2002, 27, 270–272. 10.1364/ol.27.000270. [DOI] [PubMed] [Google Scholar]
  25. Yamaguchi S.; Tahara T. Two-photon absorption spectrum of all-trans retinal. Chem. Phys. Lett. 2003, 376, 237–243. 10.1016/s0009-2614(03)00984-9. [DOI] [Google Scholar]
  26. de Reguardati S.; Pahapill J.; Rammo M.; Rebane A.. Improving the fidelity of two-photon absorption reference standards. Frontiers in Ultrafast Optics: Biomedical, Scientific, and Industrial Applications XVII, 2017; Vol. 10094, p 100941Q.
  27. Burns K. H.; Srivastava P.; Elles C. G. Absolute Cross Sections of Liquids from Broadband Stimulated Raman Scattering with Femtosecond and Picosecond Pulses. Anal. Chem. 2020, 92, 10686–10692. 10.1021/acs.analchem.0c01785. [DOI] [PubMed] [Google Scholar]
  28. Elles C. G.; Rivera C. A.; Zhang Y.; Pieniazek P. A.; Bradforth S. E. Electronic structure of liquid water from polarization-dependent two-photon absorption spectroscopy. J. Chem. Phys. 2009, 130, 084501. 10.1063/1.3078336. [DOI] [PubMed] [Google Scholar]
  29. Houk A. L.; Zheldakov I. L.; Tommey T. A.; Elles C. G. Two-Photon Excitation of trans-Stilbene: Spectroscopy and Dynamics of Electronically Excited States above S1. J. Phys. Chem. B 2015, 119, 9335–9344. 10.1021/jp509959n. [DOI] [PubMed] [Google Scholar]
  30. Pontecorvo E.; Ferrante C.; Elles C. G.; Scopigno T. Spectrally tailored narrowband pulses for femtosecond stimulated Raman spectroscopy in the range 330-750 nm. Opt. Express 2013, 21, 6866. 10.1364/oe.21.006866. [DOI] [PubMed] [Google Scholar]
  31. Ekvall K.; van der Meulen P.; Dhollande C.; Berg L.-E.; Pommeret S.; Naskrecki R.; Mialocq J.-C. Cross phase modulation artifact in liquid phase transient absorption spectroscopy. J. Appl. Phys. 2000, 87, 2340–2352. 10.1063/1.372185. [DOI] [Google Scholar]
  32. Kovalenko S. A.; Dobryakov A. L.; Ruthmann J.; Ernsting N. P. Femtosecond spectroscopy of condensed phases with chirped supercontinuum probing. Phys. Rev. A: At., Mol., Opt. Phys. 1999, 59, 2369–2384. 10.1103/physreva.59.2369. [DOI] [Google Scholar]
  33. Rai N. K.; Lakshmanna A. Y.; Namboodiri V. V.; Umapathy S. Basic principles of ultrafast Raman loss spectroscopy#. J. Chem. Sci. 2012, 124, 177–186. 10.1007/s12039-012-0214-8. [DOI] [Google Scholar]
  34. Sun Z.; Qiu X. Q.; Lu J.; Zhang D. H.; Lee S. Y. Three-state model for femtosecond broadband stimulated Raman scattering. J. Raman Spectrosc. 2008, 39, 1568–1577. 10.1002/jrs.2040. [DOI] [Google Scholar]
  35. Sun Z.; Lu J.; Zhang D. H.; Lee S. Y. Quantum theory of (femtosecond) time-resolved stimulated Raman scattering. J. Chem. Phys. 2008, 128, 144114. 10.1063/1.2888551. [DOI] [PubMed] [Google Scholar]
  36. Harbola U.; Umapathy S.; Mukamel S. Loss and gain signals in broadband stimulated-Raman spectra: Theoretical analysis. Phys. Rev. A: At., Mol., Opt. Phys. 2013, 88, 011801(R) 10.1103/physreva.88.011801. [DOI] [Google Scholar]
  37. Cen Q.; He Y.; Xu M.; Wang J.; Wang Z. Wavelength dependent resonance Raman band intensity of broadband stimulated Raman spectroscopy of malachite green in ethanol. J. Chem. Phys. 2015, 142, 114201. 10.1063/1.4914188. [DOI] [PubMed] [Google Scholar]
  38. Aloi A.; Tommasi R.. Raman Spectroscopy and Applications; Maaz K., Ed.; InTechOpen, 2017; pp 269–290. [Google Scholar]
  39. Boyd R. W.Nonlinear Optics, 3rd ed.; Boyd R. W., Ed.; Academic Press: Burlington, 2008; pp 473–509. [Google Scholar]
  40. Houk A. L.; Givens R. S.; Elles C. G. Two-Photon Activation of p-Hydroxyphenacyl Phototriggers: Toward Spatially Controlled Release of Diethyl Phosphate and ATP. J. Phys. Chem. B 2016, 120, 3178–3186. 10.1021/acs.jpcb.5b12150. [DOI] [PubMed] [Google Scholar]
  41. Gao X.; Li X.; Min W. Absolute Stimulated Raman Cross Sections of Molecules. J. Phys. Chem. Lett. 2023, 14, 5701–5708. 10.1021/acs.jpclett.3c01064. [DOI] [PubMed] [Google Scholar]
  42. Albrecht A. C. On the Theory of Raman Intensities. J. Chem. Phys. 1961, 34, 1476–1484. 10.1063/1.1701032. [DOI] [Google Scholar]
  43. Long D. A.The Raman Effect: A Unified Treatment of Raman Scattering by Molecules; Wiley and Sons, 2002; Vol. 8, pp 221–270. [Google Scholar]
  44. Prince R. C.; Frontiera R. R.; Potma E. O. Stimulated Raman scattering: From bulk to nano. Chem. Rev. 2017, 117, 5070–5094. 10.1021/acs.chemrev.6b00545. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. McCreery R. L.Raman Spectroscopy for Chemical Analysis; Wiley and Sons, 2002; pp 15–33. [Google Scholar]
  46. Dudik J. M.; Johnson C. R.; Asher S. A. Wavelength dependence of the preresonance Raman cross sections of CH3CN, SO 42-CIO 4-and NO 3-. J. Chem. Phys. 1985, 82, 1732–1740. 10.1063/1.448405. [DOI] [Google Scholar]
  47. Melnikov A. S.; Serdobintsev P. Y.; Vedyaykin A. D.; Khodorkovskii M. A. Two-photon absorption cross section for Coumarins 102, 153 and 307. J. Phys. Conf. 2017, 917, 062029. 10.1088/1742-6596/917/6/062029. [DOI] [Google Scholar]
  48. Elayan I. A.; Brown A. Degenerate and non-degenerate two-photon absorption of coumarin dyes. Phys. Chem. Chem. Phys. 2023, 25, 16772–16780. 10.1039/d3cp00723e. [DOI] [PubMed] [Google Scholar]
  49. Drobizhev M.; Tillo S.; Makarov N. S.; Hughes T. E.; Rebane A. Absolute two-photon absorption spectra and two-photon brightness of orange and red fluorescent proteins. J. Phys. Chem. B 2009, 113, 855–859. 10.1021/jp8087379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Hosoi H.; Tayama R.; Takeuchi S.; Tahara T. Solvent dependence of two-photon absorption spectra of the enhanced green fluorescent protein (eGFP) chromophore. Chem. Phys. Lett. 2015, 630, 32–36. 10.1016/j.cplett.2015.04.028. [DOI] [Google Scholar]
  51. Griffiths J. E. Raman scattering cross sections in strongly interacting liquid systems: CH3OH, C2H5OH, i-C3H7OH, (CH3)2CO, H2O, and D2O. J. Chem. Phys. 1974, 60, 2556. 10.1063/1.1681398. [DOI] [Google Scholar]
  52. Nestor J. R.; Lippincott E. R. The Effect of the Internal Field on Raman Scattering Cross Sections. J. Raman Spectrosc. 1973, 1, 305–318. 10.1002/jrs.1250010309. [DOI] [Google Scholar]
  53. Kato Y.; Takuma H. Absolute Measurement of Raman-Scattering Cross Sections of Liquids. J. Opt. Soc. Am. 1971, 61, 347–350. 10.1364/josa.61.000347. [DOI] [Google Scholar]
  54. Schomacker K. T.; Delaney J. K.; Champion P. M. Measurements of the absolute Raman cross sections of benzene. J. Chem. Phys. 1986, 85, 4240–4247. 10.1063/1.451795. [DOI] [Google Scholar]
  55. De Wergifosse M.; Houk A. L.; Krylov A. I.; Elles C. G. Two-photon absorption spectroscopy of trans-stilbene, cis-stilbene, and phenanthrene: Theory and experiment. J. Chem. Phys. 2017, 146, 144305. 10.1063/1.4979651. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ac3c02298_si_001.pdf (865.2KB, pdf)

Articles from Analytical Chemistry are provided here courtesy of American Chemical Society

RESOURCES