Summary
Large irradiation surface solar simulator often has the problem of low irradiation uniformity. Therefore, a method for designing a large irradiation surface solar simulator with high irradiation uniformity is proposed. According to the law of conservation of energy and the edge-ray principle of non-imaging optics, the free-form surface concentrator is designed and optimized by using the simulated annealing algorithm based on Bessel curve to improve the incident beam uniformity of the integrator. The optical integrator and projection system are also designed and optimized to eliminate aberrations, improve light efficiency, and enlarge the irradiation area. The design is verified using LightTools software and achieves an effective irradiation size of Φ1200 mm with an irradiance of a solar constant and an irradiation uniformity of less than 2.0%. This study provides accurate and reliable solar irradiation for laboratory calibration and performance testing of spacecraft payloads.
Subject areas: Optics, Systems engineering
Graphical abstract

Highlights
-
•
Optimization of free-form concentrator based on Bessel curve and algorithm
-
•
An object-side telecentric projection system for uniform illumination
-
•
Feasibility evaluation of solar simulation based on offset simulation of each subsystem
Optics; Systems engineering
Introduction
As a device for simulating the solar radiation environment in space in the laboratory, the solar simulator can simulate the radiation and geometric characteristics of the sun.1 It has been widely used in the fields of thermal balance experiment of spacecraft, calibration of solar photovoltaic modules, test and calibration of satellite attitude components, remote sensing technology, and solar spectrum irradiation simulation in meteorological radiation instrument verification. With the development of related technical research in the field of deep space exploration, the structural appearance of spacecraft is becoming more and more complex, and the large-irradiated surface solar simulator has more obvious advantages in spacecraft space environment simulation experiments.2,3,4,5
Using array light source illumination is one of the more direct ways to realize the simulation of solar illumination with large irradiance area. For example, Sabahi et al. used 12 xenon lamp arrays with different power to obtain 2800 mm × 2700 mm irradiation area.6 However, its irradiation nonuniformity is as high as 12.34%. Daniele et al. developed a large-scale solar simulator with adjustable irradiation,7 on the basis of the array light source, a paraboloid condenser is used to obtain an irradiance of 995 W/m2 within the size of 1700 mm × 800 mm irradiation area. And the irradiation nonuniformity reaches 5% by using up to 20 sources. Similar studies on solar simulators with array light source have shown that, more light source subunits can achieve higher irradiation uniformity. However, parameters such as spacing and distribution between light source subunits have a great influence on the irradiation uniformity,8 and the use of too many light source subunits will increase the complexity and cost of system design.
Because the space environment simulation experiment of spacecraft has more strict requirements on the performance indicators of solar simulator,9 such as irradiation area and uniformity. Therefore, most of the relevant research adopts off-axis optical system, using a single large aperture mirror or multiple small aperture mirror splicing technology to obtain a larger irradiated surface. For example, large solar simulators developed by the US, ESA, Russia, and other countries or organizations for spacecraft thermal balance experiments all use off-axis optical systems.2,10 Although this makes the irradiation surface diameter can reach 3000–6000 mm, the increase in the difficulty of assembly and the increase of structural complexity11 lead to the irradiation uniformity of only 4–15%. The solar simulator developed by Liu et al. also uses a φ2.5 m spliced collimating mirror in the off-axis optical system,12 and is equipped with four light source subunits composed of short-arc xenon lamps and ellipsoidal concentrators, which reduces the irradiation nonuniformity to 2.8%, but greatly increases the complexity of the system structure.
The concentrating system of the solar simulator, such as the ellipsoidal concentrator, the irradiance uniformity of the second focal plane will directly affect the irradiance uniformity of the whole solar simulator system.13 Wang et al. used a parabolic reflector and a Fresnel lens as an optical concentrator to change the radiation distribution of the real combined light source with two peaks into a Gaussian distribution with highly axisymmetric characteristics.14 Li et al. designed a three-dimensional compound parabolic concentrator (CPC).15 When the condensing efficiency is 85.4%, the energy distribution peak of the combined light source on the target surface is weakened by reflecting the light with nonuniform angle, so as to improve the irradiation uniformity of the target surface. Ren et al. proposed a design method of non-coaxial ellipsoidal concentrator.16 The surface is obtained by rotating the ellipse around the first focal point along the long axis at a small angle α. Although the irradiation uniformity of the second focal plane is improved, the determination of the optical axis angle α has a great impact on the energy utilization of the subsequent system, the irradiation uniformity, and the collimation angle and aperture of the collimating mirror, so it is difficult to process and adjust. Lv. et al. evolved the higher-order equation obtained by Taylor expansion of the ellipsoid equation into a deformed ellipsoid,17 and controlled the surface shape through several deformation coefficients. But this method can only determine the coefficient value by trial-and-error method, and the operability is poor.
Therefore, there is an urgent need to develop a solar radiation simulation system, which can reduce costs to a greater extent while ensuring high irradiation uniformity, and at the same time efficiently realize large-irradiated surface solar simulation to meet the increasingly urgent space environment simulation test needs.
This paper presents an optical design method for solar simulation with high irradiance uniformity and large-irradiated surface. And analyzes the factors affecting the irradiation uniformity, including the Gaussian distribution of the spot energy on the second focal plane of the concentrating system, the aberration of the optical integrator and the projection system, etc. By optimizing the design of free-form surface concentrator, aspheric optical integrator and transmissive object telecentric projection system, the small-aperture optical system is used to complete the large-irradiated surface spot simulation, and the problem of low irradiation uniformity in traditional solar simulation system with large irradiance surface is solved.
Design principle and index of optical system
For the purpose of achieving high uniformity solar irradiation simulation in a specific irradiation plane, the overall structure of the solar simulator optical system consisting of three parts: free-form surface concentrator, eliminating aberration uniform light system and object telecentric projection system, as shown in Figure 1.
Figure 1.
Overall structure of optical system
The light source is located at the first focus of the free-form surface concentrator, and the light energy emitted by the concentrator converges to its second focal plane, forming a relatively uniform radiation distribution. The irradiation surface is divided by several small element lenses in the integrator field mirror group located on the second focal plane mentioned above. At the same time, the spherical aberration and coma aberration outside the aperture axis are eliminated to prevent the deformation of the segmented image and prevent it from falling into the non-corresponding projection mirror channel. Therefore, the irradiation distribution in each small element lens is improved compared with the uniformity of the irradiation distribution on the second focal plane. Subsequently, these "uniform" segmented images are superimposed by the small element lens corresponding to the integrator projection lens group to form a beam of light at infinity. Finally, the light is converged into a uniform secondary light source surface by the superimposed condensing lens group of the object telecentric projection system, and then formed into the position of the irradiation surface by the imaging projection lens group to achieve a large area of uniform illumination. The main technical indicators of the system are shown in Table 1.
Table 1.
Main technical indicators
| Item | Target |
|---|---|
| Maximum irradiance | ≮1353 W/m2 |
| Irradiation nonuniformity | ≯2% |
| Effective irradiation area | 1200 × 1200 mm |
Selection of light source
The selection of light source in solar simulator is the primary task of system design, and the light source affects the structure, uniformity, irradiation intensity, spectral characteristics and stability of the whole system. Commonly used with solar simulator light sources are xenon lamp, LED, halogen lamp and so on. Among them, halogen lamps have the advantages of long life and good stability, but its spectrum is weak in the short-wavelength radiation, so it is commonly used as an infrared supplementary light source and is not suitable for use alone. LED has the advantages of high efficiency, low energy consumption and long service life,18 but it is difficult to improve the irradiation intensity due to the power limitation of LED devices. If the number of uses is large, it will lead to the need for a more complex spectral uniformity design, and the performance matching requirements of the selected LED are also very high, otherwise it will cause a large spectrum mismatch error. The spectrum of xenon lamp is very close to the solar spectrum, with high brightness, good consistency of optical and electrical parameters, the spectrum will not change significantly with the change of power, and the spectral quality is stable.19 The use of xenon lamp with filter can meet the requirements of irradiation uniformity, stability and spectral matching in this study. Therefore, xenon lamp is chosen as the light source of the large irradiated surface solar simulator.
Design of free-form surface concentrator
Generation of free-form surface concentrator
Aiming at the problem that the energy of the second focal plane of the traditional ellipsoid condenser is Gaussian distribution, that is, the center energy is high and the edge energy is low,20 with the goal of improving the irradiation uniformity, a design method of free-form concentrator is proposed. According to the law of conservation of energy, the edge-ray principle and the mapping method, the design of free-form concentrator is mainly divided into two steps: The first is to establish the mapping relationship between the exit angle of the light source and the corresponding point of the target surface. The second is to obtain the differential equation according to the given mapping relationship combined with the reflection law, and solve the equation by numerical method to obtain the discrete points on the free-form surface generatrix.21
Firstly, based on the point light source model, the luminous flux of the selected luminous region of the light source is calculated as22:
| (Equation 1) |
Where, is the luminous intensity of each angle of the light source, is zenith angle, which is the effective luminous angle of the light source, is a solid angle.
Short-arc xenon lamp is selected as the light source. The distribution curve of short-arc xenon lamp is axisymmetric distributed, and the luminescence angle ranges from 20° to 125°. The distribution curve of short-arc xenon lamp is shown in Figure 2. Take the light distribution curve data of the xenon lamp as the luminous intensity corresponding to the effective luminous angle of the light source, and do numerical integration on Equation 1 to calculate the luminous flux in the discrete interval as follows23:
| (Equation 2) |
where, take as the average value of luminous intensity in .
Figure 2.
Diagram of light distribution curve of short arc xenon lamp
As shown in Figure 3A, according to the principle of mapping method, the luminous flux in the discrete interval is mapped to the ring in the on the target surface, where is the illumination on the target surface. In order to obtain uniform irradiation distribution, is taken, and the luminous flux in the ring on the target surface is:
| (Equation 3) |
Figure 3.
The energy mapping relationship and relative position relationship among light source, the free-form surface and the target surface
(A) Schematic diagram of energy mapping between light source and target surface.
(B) Schematic diagram of the relative positions of the light source and the free-form surface and the target surface.
According to the law of conservation of energy, assuming that there is no energy loss in the process of light transmission, that is, all the energy emitted by the light source is transmitted to the target plane after reflection, it can be considered that and are equal:
| (Equation 4) |
Using the Equation 4, combined with the initial conditions (the light emitted by the light source at a light emitting angle of 20 is reflected to the target surface at R = 0 through the free-form surface), the mapping relationship between the light source emitting angle and the corresponding point on the target surface can be obtained. As shown in Figure 3B, the coordinates of the points on the free-form surface generatrix are , and the coordinates of the corresponding points on the target surface are .
The unit vector of incident light is:
| (Equation 5) |
The unit vector of outgoing light is:
| (Equation 6) |
where
The tangent vector of the reflection point is:
| (Equation 7) |
The law of reflection is:
| (Equation 8) |
Bring Iout, Iin and It into the above equation, the resulting equation is:
| (Equation 9) |
The result of the calculation is:
| (Equation 10) |
In order to match the subsequent optical system and meet the principle of system pupil connection, the relative aperture commonly used in solar simulator system is taken as 1/4,24 The back opening of the free-form surface is used to limit the edge light, and the angle of the light converged by the free-form surface concentrator to the incident surface of the integrator is controlled to ensure that the light convergence angle is within ±7°. Determination of back opening radius of free-form surface by geometric relationship:
| (Equation 11) |
where, the maximum effective luminous angle of the light source is 125°; is the distance between the light source and the target surface.
Taking the concentrator of a solar simulator as an example, the working distance from the first focus to the second focus can be set to 1500 mm. Substituting and into Equation 11, we can get that the opening radius of the free-form surface concentrator is about 172 mm, and then calculate the starting point coordinates of the free-form surface generatrix. Considering the connecting principle of pupil between concentrator and uniform system and the processing of integrator element lens, the radius of the second focal plane is about 30 mm. The coordinates of discrete points on the free-form surface generatrix are calculated by Runge-Kutta methods,25 and finally the radius of the front opening of the free-form surface concentrator is about 17 mm by iteration. The calculated coordinates of discrete points are imported into the 3D modeling software, and all discrete points are fitted into curves by using the B-spline construction function in the software. Then rotate the fitted curve around the z axis to obtain a three-dimensional solid model of the free-form concentrator.
The method of multi-parameter optimization of free-form spotlight mirrors based on Bezier curve
Due to the fact that xenon lamps are extended light sources with a certain area, the free-form spotlight designed for point sources in this paper experiences significant reduction in irradiance uniformity on the target surface when introducing extended light sources, thus requiring feedback optimization. The discrete point coordinates of the free-form spotlight’s contour line are calculated using the Fresnel equation. These coordinates are then fitted into a Bezier curve, and the corresponding Bezier control point coordinates, tangent lengths, and angles that control the curve’s contour are calculated through inverse calculation. By changing the control point coordinates, tangent lengths, and angles, the curve’s contour can be altered, thereby changing the angle of light reflection. The functional expression for the Bezier curve is26:
| (Equation 12) |
Where, is the control point of the Bezier curve, is a Bernstein basis polynomial of order q, can be expressed as .
The entire curve profile is subdivided, and the optimization variables, evaluation functions, and optimization algorithms are selected for each subdivided curve profile to improve the irradiance uniformity of the target surface of the free-form spotlight.
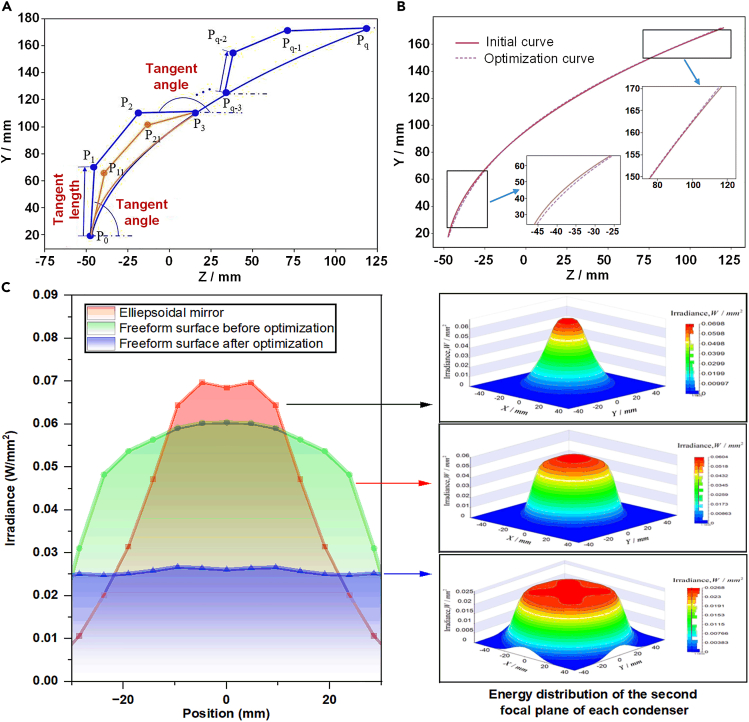
Taking the first segment of the subdivided curve outline as an example, the subdivided curve outline represented by P0 to P3 can be expressed by the coordinates of control points P1 and P2, as well as their corresponding tangent angles and lengths. When the coordinates of the control points change from P1 and P2 to P11 and P21, the subdivided curve outline changes. Therefore, the coordinates of P1 and P2 and their corresponding tangent angles and lengths are selected as optimization variables to optimize the subdivided curve outline, as shown in Figure 4A.
Figure 4.
Method and results of multi-parameter optimization of free-form surface concentrator based on Bessel curve
(A) Schematic diagram of the contour line of the free-form surface concentrator constructed by Bezier curve.
(B) Comparison of initial structure and optimized structure contour line.
(C) Irradiance distribution of target surface of ellipsoid concentrator and free-form surface concentrator before and after optimization.
Taking the irradiation uniformity of the simulated free-form surface concentrator target surface as the evaluation function, the irradiated surface is meshed, and the illuminance on the irradiated surface is normalized to obtain:
| (Equation 13) |
Where, is the illuminance on the target irradiated surface; is the maximum illuminance on the target irradiated surface; is the normalized illuminance on the target irradiated surface; is the evaluation function of Bezier curve optimization; and are the variables in the horizontal and vertical directions of the grid.
The text describes the optimization of a Bezier curve using simulated annealing algorithm.27,28 The algorithm involves setting the initial temperature Tinitial and final temperature Tfinal for the annealing process, as well as the initial optimization parameters and the evaluation function for the Bezier curve. The algorithm iterates M times at each temperature to fully search the solution space. During the search process, if the evaluation function of the current solution is smaller than the previous solution , then is accepted. If the evaluation function of the current solution is greater than that of the previous solution , then a probability of accepting the solution, which is dependent on the temperature, is generated. It can be seen that as the temperature decreases, the probability of accepting a worse solution decrease, gradually shifting from a broad search of the solution space to a deep search.
| (Equation 14) |
where, is the temperature; is the evaluation function corresponding to .
The temperature change during the optimization can be expressed by the Equation 15, and the temperature update parameter selected here can be set to 0.8529:
| (Equation 15) |
The following equation describes the relationship between th-order variable values and th-order variable values in the algorithm optimization:
| (Equation 16) |
Here, is a random vector uniformly distributed within (−1,1), with a dimension equal to that of the optimization variables. is a diagonal matrix defining the maximum allowable change in each variable.
Throughout the optimization process, the optimization ends when the temperature changes to . At this point, the Bezier curve constructed from the optimized control point coordinates, corresponding tangent angles, and lengths represents the optimal free-form surface concentrator contour. The output is the optimized free-form surface concentrator shape. As shown in Figures 4B and 4C, which illustrate the three-dimensional point cloud model before and after optimization, the comparison diagram of its initial structure and optimized structure contours, and the target surface irradiance distribution comparison between the ellipsoidal spotlight and the optimized free-form surface concentrator.
From Figure 4B, we can observe the trend of the contour line before and after optimization, The surface shape gradually shrinks toward the larger aperture, and the contour line is relatively lower at small aperture angles and relatively upward at large aperture angles. This allows the reflected light rays at smaller aperture angles to project at higher height values on the second focal plane, and lower height values for larger aperture angles, thus improving the irradiance distribution uniformity on the second focal plane. Figure 8 shows the irradiance uniformity of both the traditional ellipsoidal concentrator and the optimized free-form surface concentrator. Within the Φ60 mm target surface, the irradiance nonuniformity of the traditional ellipsoidal concentrator reaches 73.5%, while that of the optimized free-form surface concentrator decreases from 32.1% before optimization to 3.7% after optimization.
Figure 8.
Simulation diagram of overall optical system
To sum up, the free-form surface design method involved in this study firstly adopts the efficient mapping method for point-light source design, and then adopts the simulated annealing algorithm to achieve efficient machine learning feedback optimization for the free-form surface type of the pointed light source, so as to obtain the free-form surface type of the extended light source that meets the conditions of the real light source. The whole design process can not only make up for the approximate deviation caused by the difficulty of the mapping method to meet the integrability condition,30 but also solve the problem that the traditional Feedback Design Optimization is difficult to choose the initial structure, and avoid the local optimal solution trap caused by the initial structure selection deviation.31,32 It can also achieve the maximum improvement of optimization efficiency.33
Design of uniform optical system to eliminate aberrations
Design of uniform light system under free-form concentrator
Optical integrator is the core component of uniform light system. It consists of two sets of lens arrays arranged symmetrically before and after. The lens array of the front group is a field lens group,and the rear one is a projection lens group. The aperture, focal length, and thickness of the two sets of lens array element lenses are the same, and they are at each other’s focal plane position.34
Make the exit pupil of the free-form concentrator lens MN. The center points of the three small lenses on the optical integrator field lens set are O1, O2, and O3. As shown in Figure 4A. The field mirror group element lens imprints the pupil of the concentrator on the corresponding element lens of the projection lens group, avoiding the loss of light energy. The elemental lenses and rear auxiliary mirrors of the projection lens group image the corresponding elemental lenses of field lens group onto the irradiated surface PP'. At this time, since the irradiation surface and each field lens group element lens are conjugated, and the light emitted by the light source is modulated by the free-form concentrator, the irradiation distribution on the field lens group has a mapping relationship with each discrete interval on the condenser. Therefore, uniform illumination can be achieved when the image of the element lens of the field lens group overlaps on the irradiated surface. According to the experience of calculating the number of integrator lenses, combined with the requirements of system uniformity, the number of integrator channels is selected as 36, and the shape of the elemental lens is square.35,36
Combined with the design principle of free-form concentrator, the incident light of each small element lens of the field lens group only comes from a discrete interval corresponding to it on the MN, so the stray light caused by the aberration of integrator will seriously affect its uniform effect. Among them, the off-axis spherical aberration of diaphragm and coma have the greatest influence on the integrator. On the one hand, this causes the position of the image surface of the superimposed image of each channel to be incorrect with its theoretical position, and at the same time deforms the image formed by each channel and changes the shape of the superimposed image surface. On the other hand, the off-axis spherical aberration of diaphragm and coma cause those rays emitted at the edge of each discrete interval on the pupil to pass through the edge of the field mirror element lens, falling into the projection lens element lens that has a different optical path than the field lens element lens, becoming harmful stray light. Therefore, effective suppression of the above stray light by correcting for aberrations is considered.
Aberration correction of uniform system
Zemax software auto-optimization is used to correct the aberration of each channel of the integrator individually. Taking the center channel as an example, the half field of view angle is 0°, 3.5°, 7°. The rear surface of the lens is optimized for aspheric and set to an even-order aspheric surface. In order to reduce the complexity of the processing process, only the quadratic conic coefficient and quadratic term coefficient of the aspheric surface are optimized. The edge light height is set, and the parameters are shown in Table 2. The optical path, spot diagram and irradiance diagrams of the lens before and after optimization are shown in Figures 5B–5G.
Table 2.
Structural parameters of the central lens
| Lens name | Radius (mm) | Interval (mm) | Material | Caliber (mm) |
|---|---|---|---|---|
| Central eyelet lens | ∞ | 8 | F_SILICA | 6.7 |
| −24.66 | 53.2 | 6.7 |
Figure 5.
Design principle and optimization result of optical integrator
(A) Imaging principle diagram of optical integrator.
(B) Optical path diagram of center lens before optimization.
(C) Optical path diagram of center lens after optimization.
(D)Spot diagram before optimization.
(E) Spot diagram after optimization.
(F) Integrator superimposed image plane irradiance map before optimization.
(G) Integrator superimposed image plane irradiance map after optimization.
As can be seen from Figures 5D and 5E, the aberration before and after optimization has been effectively corrected, and the radius of diffuse spots after optimization of each field of view is nearly one-fifth of the initial value. It can be seen from Figures 5F and 5G that the edges of the irradiance map of the superimposed image surface of the optimized integrator are clear and sharp, and the irradiation uniformity is significantly better than that before optimization, which effectively avoids the influence of imaging stray light on irradiation uniformity caused by large spherical aberration and coma.
Design of object telecentric projection system
Considering that the traditional coaxial optical system has the problem that the size limitation of the glass blank cannot achieve the large optical aperture, and the traditional off-axis reflective optical system also has problems such as large structure, low compactness, high cost, and inability to meet the requirements of high irradiation uniformity, this paper designs a transmissive object telecentric projection system based on the principle of Kohler illumination. The optical path diagram is shown in Figure 6. The whole system has compact structure, convenient assembly and adjustment, low cost, and can realize uniform illumination of large irradiation surface under small-diameter optical system. The system consists of a superimposed condenser lens group and an imaging projection lens group. The function of the superimposed condenser lens group is to concentrate the parallel light emitted by the integrator in the same direction at its rear focal plane to form a uniform virtual image surface. The function of the imaging projection lens group is to image the uniform virtual image surface at the irradiated surface to achieve uniform illumination of the large irradiated surface. At the same time, the pupil of the optical integrator is imaged by superimposed condenser lens group at the position of imaging projection lens group, which not only ensures the uniformity of the image surface, but also ensures that the optical integrator matches the pupil of the projection system.
Figure 6.
Optical path diagram of transmissive object telecentric projection system
In the whole design process of the projection system, in order to achieve higher requirements for solar irradiation simulation, it is necessary to consider the influence of aberration on technical indicators such as uniformity. Therefore, the spherical aberration, coma, and field curvature of the superimposed condenser lens group are corrected. Using the negative spherical aberration of the positive spherical aberration balance system generated by the negative lens, the positive and negative lenses are kept away from the correction field curvature, and the negative lens is bent toward the diaphragm as much as possible to avoid the asymmetry of the beam and reduce the coma of the system. The imaging projection lens group adopts the structural form of three-separated objective lens, and its requirements for glass combination are relatively free. Glass materials with large differences in refractive index value and dispersion value can be used to balance the residual aberration of the optical system of the previous group on the one hand, and reduce the chromatic aberration and spherical aberration of the projection system on the other hand, and improve the illumination quality of the irradiated surface. The parameters are listed in Table 3.
Table 3.
Structural parameters of the object telecentric projection system
| Lens type | Radius (mm) | Interval (mm) | Material | Caliber (mm) |
|---|---|---|---|---|
| STANDARD | −4.83E+01 | 6.53E+00 | H-ZF88 | 7.50E+01 |
| STANDARD | −5.20E+01 | 1.41E+02 | 7.50E+01 | |
| STANDARD | −2.03E+04 | 1.48E+01 | H-LAK52 | 1.16E+02 |
| STANDARD | −2.49E+02 | 3.29E+01 | 1.16E+02 | |
| STANDARD | −1.37E+02 | 7.73E+00 | H-ZF88 | 1.18E+02 |
| STANDARD | −2.33E+02 | 1.06E+02 | 1.18E+02 | |
| STANDARD | −2.58E+03 | 4.73E+01 | H-ZLAF69 | 1.53E+02 |
| STANDARD | −2.73E+02 | 7.20E+02 | 1.53E+02 | |
| STANDARD | −1.32E+02 | 5.44E+01 | H-ZF88 | 1.88E+02 |
| STANDARD | −1.69E+02 | 1.14E+02 | 1.88E+02 | |
| STANDARD | 5.75E+02 | 7.99E+01 | H-LAK52 | 2.22E+02 |
| STANDARD | −3.67E+02 | 4.81E+01 | 2.22E+02 | |
| STANDARD | −2.77E+02 | 4.24E+01 | H-ZF88 | 1.98E+02 |
| STANDARD | −5.35E+02 | 1.00E+03 | 1.98E+02 |
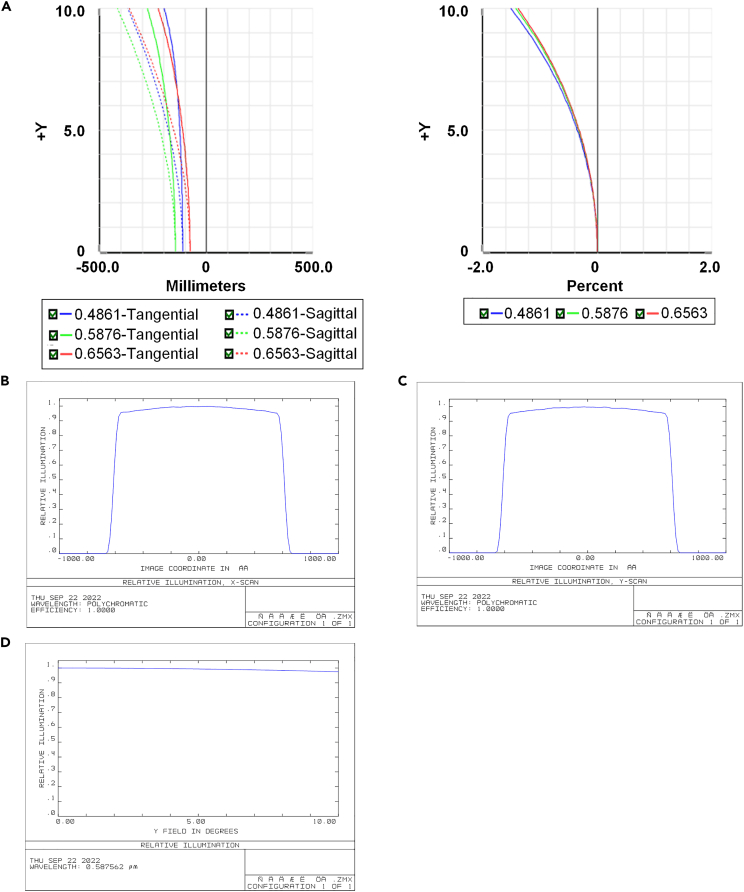
Since the projection system of the solar simulator is a non-imaging optical system, it mainly evaluates the field curvature, distortion and illumination uniformity of the indexes. Figure 7A is the image plane field curvature and distortion diagram of the system, from which it can be seen that the image plane distortion is less than 2%. Figures 7B and 7C shows the contrast curve of the image plane of the system in the X and Y directions. According to the curve, it can be seen that in the irradiation surface range of φ1200 mm, the illuminance change in the X direction and the Y direction is consistent. Figure 7D shows the contrast curve of the image plane of the system. The contrast degree of the system in each field of view is greater than 0.98, which has good irradiation uniformity, and the design results meet the actual requirements of the simulator.
Figure 7.
Design results of object telecentric projection system
(A) Field curvature and distortion diagram.
(B) Relative illuminance in X direction of irradiated surfaces.
(C)Relative illuminance in Y direction of irradiated surfaces.
(D) Relative illuminance curve of each field of view.
Results
Simulation analysis of optical system
According to the size and layout of the optical system, the optical system model was established with LightTools software, and the light flux entering the receiving surface was determined by Monte Carlo ray tracing method. According to the previous engineering experience,37 the power of the short-arc xenon lamp is determined to be 10000 W, the number of sampled rays is set to 1 × 108, and the simulation diagram of the solar simulation system is shown in Figure 8.
It can be seen from Figure 9A that the central energy of the irradiated surface of the solar simulation system using the traditional ellipsoid concentrator fluctuates up and down, the color of the irradiated surface from the center to the edge from dark to light, and the irradiance from high to low. Figure 9B shows that the irradiation surface of the solar simulation system using free-form concentrator is relatively uniform from the center to the edge. 17 sampling points are selected in the irradiation surface of the system, and the irradiation surface 600 mm and 1200 mm are measured in turn, and the irradiation nonuniformity of the irradiation surface is calculated as follows:
| (Equation 17) |
Where, is irradiation nonuniformity; is the maximum irradiance on the irradiated surface; is the minimum irradiance on the irradiated surface; is the irradiation nonuniformity of the solar simulation system when using ellipsoidal concentrator; is the irradiation nonuniformity of the solar simulation system when using free-form concentrator. The measurement data is substituted into Equation 17 for calculation. The results are shown in Table 4 and Figure 10.
Figure 9.
Irradiation distribution of solar simulator using ellipsoid or free-form surface concentrator
(A) Irradiation distribution of a solar simulator using ellipsoid concentrator.
(B) Irradiation distribution of a solar simulator using free-form concentrator.
Table 4.
Comparison of irradiation nonuniformity of solar simulator irradiation surface using ellipsoidal condenser and free-form surface condenser
| Diameter/mm | Free-form surface condenser |
Ellipsoid condenser |
||
|---|---|---|---|---|
| /(W·m−2) | /(W·m−2) | /(W·m−2) | /(W·m−2) | |
| 600 | 1597.68 | 1574.62 | 1652.78 | 1605.40 |
| 1200 | 1597.68 | 1550.47 | 1652.88 | 1561.01 |
Figure 10.
Comparison analysis diagram of irradiation inhomogeneity of solar simulator using ellipsoid concentrator and free-form surface concentrator
It can be seen from the data in Table 3 that compared with the traditional ellipsoid concentrator, the use of free-form concentrator as the solar simulation concentrator system can improve the irradiation uniformity of the irradiation surface, and the irradiation nonuniformity is reduced from 4.51% to 1.49% within the irradiation surface Φ1200 mm. This is due to the fact that free-form concentrator improve the uniformity of irradiation distribution at the incident surface of the integrator. At the same time, the optical integrator is corrected for aberration, which greatly improves the uniform light ability of the system. Cooperate with the object telecentric projection system, so as to ensure the large irradiation area while improving the irradiation uniformity of the whole system.
Discussion
Error analysis of solar simulation optical system
In order to evaluate the feasibility of processing and assembly of high uniformity large irradiated surface solar simulation system based on free-form surface concentrator, the influence of possible errors of solar simulator system on its optical performance is simulated and analyzed.38,39 Taking the irradiance and irradiation nonuniformity within 1200 mm of the irradiation surface as the evaluation index, the effects of the surface accuracy of free-form concentrator, the angle offset of the concentrating system and axial, vertical position offset of the concentrating systems, homogenizing systems and projection systems on irradiance and irradiation nonuniformity were analyzed respectively.
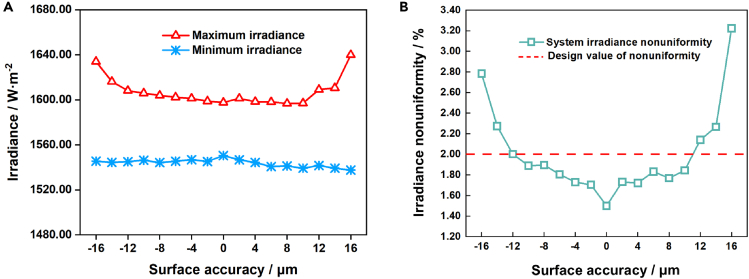
In Figure 11, since the designed free-form concentrator is rotationally symmetric, the basic variable that determines its surface accuracy is the discrete point coordinate position of the generatrix of the fitted free-form concentrator. Therefore, in LightTools software, the program that externally controls the position offset range of the generatrix of the free-form concentrator is externally connected, and the corresponding free-form concentrator surface type is fitted to the different position offset values of each discrete point, so as to simulate and analyze the influence of the surface type accuracy of the free-form concentrator on the irradiance and irradiation nonuniformity of the solar simulator. The results show that when the surface accuracy is less than ±10 μm, the large angle stray light caused by the irregular surface increases rapidly,40 which in turn causes more beams of the small lenses of the optical integrator field lens group to enter the small lenses of the projection lens group of adjacent channels, and finally forms an abnormal point of irradiation distribution on the irradiated surface, which greatly destroys the uniformity of the irradiated surface.
Figure 11.
Influence of surface shape accuracy of free-form concentrator on irradiance and irradiation nonuniformity
(A) Irradiance.
(B) Irradiation nonuniformity.
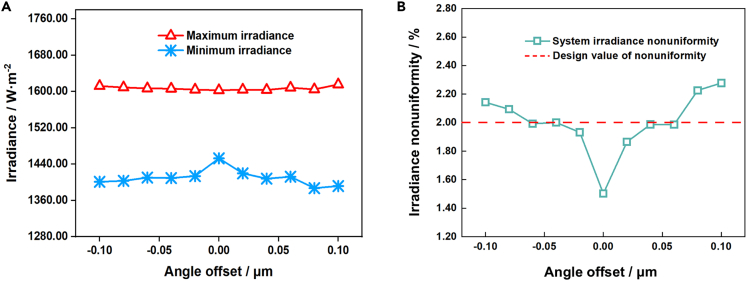
In Figure 12, the angular offset of the concentrator not only causes the energy center of the target irradiation surface of the concentrator to deviate from the geometric center of the optical integrator, but also causes a large number of beams ejecting the small lenses of the optical integrator field lens group into the small lenses of the projection lens group of adjacent channels, resulting in a more serious cross talk between the lenslets.41 So, the overall energy on the irradiated surface shows a downward trend and the nonuniformity gradually increases.
Figure 12.
Effect of angular offset of free-form concentrator on irradiance and irradiation nonuniformity
(A) Irradiance.
(B) Irradiation nonuniformity.
Figure 13 shows the variation trend of irradiance and nonuniformity of each system within ±0.04 mm along the axial position and the vertical position, where the position offset step size is selected by 0.01 mm. The central position of each group of experiments represents the distribution of irradiated surfaces without position offset. In the figure, since the overall system is a coaxial transmission optical structure, the farther away the subsystems are from the irradiation surface under the same position offset, the greater the error between the light path and the ideal light path during the optical transmission process, and the greater the cumulative impact on irradiance and nonuniformity. At the same time, because the free-form concentrator maps each discrete interval with the target plane one by one when designing, resulting in the system being more sensitive to defocus caused by the axial offset. Therefore, in the same subsystem, the axial offset is more affected by the irradiance and nonuniformity than the vertical offset.
Figure 13.
Effect of concentrating system, homogenization system and projection system on irradiance and irradiation unevenness under the offset of ±0.4 mm along the axial position and the vertical position
It can be seen from Figures 11, 12, and 13 that when position offset along axis and vertical axis of free-form concentrator, axial position offset of uniform system are better than 0.2 mm, and the surface accuracy of the free-form concentrator is better than 10um, the solar simulator can achieve solar simulation with a high uniformity large irradiated surface with irradiance greater than 1S0 and irradiation nonuniformity less than 2.0% within 1200 mm. In addition, the vertical axis position offset of the uniform system and the axis and vertical axis position offset of the projection system have little influence on the irradiation nonuniformity and irradiance of the solar simulator, and can meet the irradiation design requirements within the error range of 0.4 mm.
According to the existing processing and detection level, the surface shape accuracy can be better than 10 um.42,43,44 Considering the overall optical structure volume, split installation was adopted, that is, the system was divided into four parts: free-form concentrator, uniform light system, superimposed condensing lens group and imaging projection lens group. First of all, each part is placed in its own adjusting frame for each part to be adjusted separately, and then the position between the four adjusting frames is adjusted. The offset of the displacement can be fine-tuned according to the simulation results in this section.
In summary, the irradiation uniformity of the designed solar simulator with large irradiation surface and high irradiation uniformity meets the Class A standard of IEC 60904-9:2020.45
Spectral mismatch and temporal instability of irradiance are important technical indexes for evaluating the performance of solar simulators. This problem is also fully considered in the solar simulator designed in this paper. By using xenon lamp as the light source and combining with the design of filter, the A Class standard of spectral matching degree and irradiation instability of the solar simulator can be achieved. However, due to space constraints, it will not be discussed in detail here.
Conclusion
Aiming at achieving high irradiation uniformity solar spot simulation, a solar simulator optical system for laboratory calibration and performance testing of optical remote sensors is designed. A free-form concentrator is proposed as a concentrating system, which not only ensures the concentrating efficiency, but also improves the irradiation uniformity of the second focal plane position. The optical integrator is optimized to solve the problem of stray light caused by aberration affecting the uniformity of irradiation. By designing the object telecentric projection system, the simulation of large irradiated surface spot under the small-aperture optical system is realized, and the irradiance deviation between the edge and the center of the irradiated surface is reduced. The influence of free-form concentrator surface type and position offset of each system on irradiation nonuniformity is simulated and analyzed, which verifies the feasibility of processing, detection and assembly of the system. The final results show that in the irradiation surface of 1200 × 1200 mm, the irradiance reaches a solar constant, and the irradiation nonuniformity is lower than 2.0% and the lowest can reach 1.5%, which realizes the simulation of large irradiation area and high irradiation uniformity solar spots.
The technology involved in this study provides technical reference and reference for the development of solar simulator for remote sensing, which is of certain significance for the diversified development of aerospace remote sensing products.
Limitations of the study
Spectrum is also a relatively important physical property of sunlight. In this study, xenon short-arc lamp with excellent performance is selected as the light source in order to obtain spectral characteristics similar to that of sunlight. In order to meet the requirements of higher spectral match, the future research should be carried out in the selection of light source and spectrum modulation.
STAR★Methods
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Software and algorithms | ||
| OpticStudio 19.4 | Zemax | Zemax |
| MATLAB 2022 | MathWorks | MATLAB (mathworks.com) |
| Light Tools | Optical Research Associates | Synopsys | EDA Tools, Semiconductor IP and Application Security Solutions |
Resource availability
Lead contact
Further information and requests for resources, measurement procedures and data can be directed to the lead contact, Shi Liu (liu_shi_ls@163.com).
Materials availability
This study did not generate new unique reagents.
Method details
| Nomenclature and units | |
|---|---|
| luminous flux [lm] | |
| luminous intensity [Cd] | |
| zenith angle [°] | |
| solid angle [°] | |
| illumination [lx] | |
| luminous flux in the target ring surface[lm] | |
| unit vector of incident light [/] | |
| unit vector of outgoing light [/] | |
| tangent vector of the reflection point [/] | |
| relative aperture [/] | |
| back opening radius [mm] | |
| working distance [mm] | |
| control point of the Bezier curve [/] | |
| Bernstein basis polynomial of order q [/] | |
| illuminance on the target irradiated surface [lx] | |
| maximum illuminance on the target irradiated surface [lx] | |
| normalized illuminance on the target irradiated surface [/] | |
| evaluation function of Bezier curve optimization [/] | |
| variables in the horizontal [/] | |
| vertical directions of the grid [/] | |
| Tinitial | initial temperature [°C] |
| Tfinal | final temperature [°C] |
| initial optimization parameters [/] | |
| random vector uniformly distributed within (−1,1) [/] | |
| diagonal matrix [/] | |
| irradiation nonuniformity [%] | |
| maximum irradiance [W/m2] | |
| minimum irradiance [W/m2] | |
| irradiation nonuniformity of the solar simulation system when using ellipsoidal concentrator [%] | |
| irradiation nonuniformity of the solar simulation system when using free-form concentrator [%] |
Modeling
The modeling experiment was conducted on the optical design software platform Lighttools developed by Optical Research Associates. The concentrator designed using the freeform surface method calculated by MATLAB software (Figure 3) can be imported into Lighttools using its built-in “surface modeling” function. At the same time, the projection system lens designed by Zemax software (Figure 6) is also imported into Lighttools.
It should be noted that the surface and material properties of the lens will be lost during importation, so it is necessary to separately set the material and surface properties of the concentrator, projection lens, and aperture (Table 3). Among them, “simple mirror” is used for the surface property of concentrator, “smooth optical” is used for transmission lens surface property, and “absorber” is used for aperture surface property. In order to improve simulation efficiency and verify feasibility effectively, an appropriate transmittance and reflectance can be selected in “smooth optical”; if there are mechanical surfaces involved, “Probabilistic Ray Split” function can be added.
In the theoretical design work distance (Table 3), a 'dummy surface' is set up, and 'receivers' are placed on it to observe the final ray tracing results. The working distance here often refers to the distance from the last surface of the system’s lens to the ideal receiving surface.
After establishing the model, Monte Carlo ray tracing method is used with 1x108 rays selected for tracing. Monte Carlo ray tracing is a probability-based statistical algorithm that simulates the propagation of light in a scene through random sampling, thus achieving realistic rendering of scenes. The selection of ray quantity takes into account both "the more rays, the more realistic" and "increasing ray quantity beyond a certain point does not significantly improve realism". If there are more complex mechanical surfaces, it is recommended to increase the number of rays to ensure sufficient quantity reaching Receivers; or use importance sampling function to increase the probability of rays reaching specific areas.
After completing tracing, an intuitive irradiance distribution map can be directly obtained for the irradiation surface (Figure 9), or grid energy data can be outputted for further analysis (Figures 10, 11, 12, and 13).
Acknowledgments
This work was supported by the 111 Project of China (D21009), Jilin Scientific and Technological Development Program (20210201034GX), National Natural Science Foundation of China (61603061), and Jilin Province Innovation and Entrepreneurship Talent Funding Project (2023QN13).
Author contributions
Conceptualization, Methodology, Formal analysis, Writing – original draft, Visualization, S.L. and J.Z.; Writing – review and editing, J.Z. and G.Z.; Investigation, Y.Z., S.Z., G.Z., and L.L.; Project administration, Funding acquisition, S.L., S.Y., and Y.Z.
Declaration of interests
The authors declare no competing interests.
Inclusion and diversity
We support inclusive, diverse, and equitable conduct of research.
Published: August 17, 2023
Data and code availability
-
•
All data reported in this paper will be shared by the lead contact upon request.
-
•
The codes are available on reasonable request from the lead contact.
-
•
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
References
- 1.Meng Q., Li Y., Gu Y. Dynamic Mesh-Based Analysis of Irradiance Characteristics of Solar Simulator. Optik. 2015:4658–4664. doi: 10.1117/12.2060645. [DOI] [Google Scholar]
- 2.Eddy R. SPACE SIMULATION CONFERENCE; 1968. Design and Construction of the JPL SS15B Solar Simulator. [Google Scholar]
- 3.Petrasch J., Coray P., Meier A., Brack M., Haeberling P., Wuillemin D., Steinfeld A. A novel 50kW 11,000 suns high-flux solar simulator based on an array of xenon arc lamps. J. Sol. Energy Eng. 2007 doi: 10.1115/1.2769701. [DOI] [Google Scholar]
- 4.Bodnár I., Koós D., Iski P., Skribanek Á. Design and construction of a sun simulator for laboratory testing of solar cells. Acta Polytechnica Hungarica. 2020;17:165–184. doi: 10.12700/aph.17.3.2020.3.9. [DOI] [Google Scholar]
- 5.Sun M., Zhang G., Yang B., Tao X., Ding G. IEEE; 2012. Optical System Design of Solar Simulator for Testing Meteorological Radiation Instrument; pp. 600–603. [DOI] [Google Scholar]
- 6.Hudisteanu, S.V., Chereches, C.N., Turcanu, F.E., Taranu, N., Verdes, M., Ancas, A.D., Hudisteanu, I., Ungureanu, D., and Polcovnicu, R.A. Solar radiation simulation device for investigation of thermal and photovoltaic panels. DOI: 10.54684/ijmmt.2022.14.3.76
- 7.Colarossi D., Tagliolini E., Principi P., Fioretti R. Design and validation of an adjustable large-scale solar simulator. Appl. Sci. 2021;11:1964. doi: 10.3390/app11041964. [DOI] [Google Scholar]
- 8.Martínez-Manuel L., Wang W., Peña-Cruz M.I. Optimization of the radiative flux uniformity of a modular solar simulator to improve solar technology qualification testing. Sustain. Energy Technol. Assessments. 2021;47:101372. doi: 10.1016/j.seta.2021.101372. [DOI] [Google Scholar]
- 9.Li J., Zhang L., Si X., Li X., Liu H., Wang J., Shi J., Chen H., Zhu X., Han H. Ten-dimensional scanning system of scanning xenon lamp solar simulator. Opt Precis. Eng. 2017;25:358–366. doi: 10.3788/ope.20172502.0358. [DOI] [Google Scholar]
- 10.Frey . 1982. Study of a Large Solar Simulator at ESTEC; pp. N83–N13127. [Google Scholar]
- 11.Sun Y., Xia Z., Han H., Chen L., Liu R., Chen G., Wang K. Alignment of collimator and test of radiation characteristics for large solar simulator. Infrared Laser Eng. 2019;48:268–272. doi: 10.3788/irla201948.0417006. [DOI] [Google Scholar]
- 12.Liu J., Deng R., Wang J., Zeng K. Design of 2.4 m solar simulator. Infrared Laser Eng. 2015;44:3348–3352. doi: 10.1088/1612-2011/12/7/075402. [DOI] [Google Scholar]
- 13.IEC . International Electrotechnical Commission [iec]; 2007. Solar Simulator Performance Requirements. IEC 60904-9 Ed. 1.0 en:1995. [Google Scholar]
- 14.Wang W., Aichmayer L., Laumert B., Fransson T. Design and validation of a low-cost high-flux solar simulator using Fresnel lens concentrators. Energy Proc. 2014;49:2221–2230. doi: 10.1016/j.egypro.2014.03.235. [DOI] [Google Scholar]
- 15.Ren L., Wei X., Niu W., Wang H., Xu W., Xiao J., Lu Z. A high flux solar simulator based on an array of non-coaxial ellipsoidal reflector. Acta Opt. Sin. 2012;32:220–225. doi: 10.3788/aos201232.1022002. [DOI] [Google Scholar]
- 16.Lv T., Zhang J., Fu D., Chen X., Liu J. A deformed ellipsoid condenser beneficial to the uniformity of the solar simulator. Acta Opt. Sin. 2013;33:253–257. doi: 10.3788/aos201333.1223001. [DOI] [Google Scholar]
- 17.Ming S., Sun G., Zhang G., Liu S., Xu D., Yang S., Su S., Zhang J., Zhang R. Continuous regulation system design of wide-range irradiance for solar simulators. Acta Opt. Sin. 2021;41:176–184. doi: 10.3788/aos202141.1622002. [DOI] [Google Scholar]
- 18.Hu P., Wang G., Wang J., Ou L., Zhu X. Study of high spectrum matching LED solar simulator. Auto. Instrumentation. 2020;249:85–89. doi: 10.20508/ijrer.v10i1.10335.g7860. [DOI] [Google Scholar]
- 19.Li, Q., Wang, C., Cha, J., and Xia, W. Spectral Characteristic of Short-Arc Xenon Lamp and Application in Solar Simulators. Spectrosc. Spectr. Anal. 32:1447-1450. DOI: 10.3964/j.issn.1000-0593(2012)06-1447-04 [PubMed]
- 20.Ma Y. Zhejiang University of Technology; 2014. Research on Lighting Design and Optimization Method of Free-form Surfaces. [Google Scholar]
- 21.Li L., Wang B., Pottas J., Lipiński W. Design of a compound parabolic concentrator for a multi-source high-flux solar simulator. Sol. Energy. 2019;183:805–811. doi: 10.1016/j.solener.2019.03.017. [DOI] [Google Scholar]
- 22.Chen J., Gu G. Construction of free-form reflector by mapping method. Journal of Changchun University of Science and Technology (Natural Science Edition) 2013;36:1–5. doi: 10.3969/j.issn.1672-9870.2013.06.001. [DOI] [Google Scholar]
- 23.Zhu X., Li H., Xue Y., Qi Y. Optical design and uniformity simulation of reflector. Electro-Optic Technol. Appl. 2010;25:18–21. doi: 10.3969/j.issn.1673-1255.2010.06.006. [DOI] [Google Scholar]
- 24.Gao Y., Liu H., Wang L., Gu G. Design and development of large area collimated solar simulator. Chinese Optics. 2014;7:657–664. doi: 10.3788/co.20140704.0657. [DOI] [Google Scholar]
- 25.Yi D., Shen Y., Li Y. Zhejiang University Press; 2002. Calculation Method; pp. 240–248. [Google Scholar]
- 26.Liang W., Li Y., Fan L., Wang Q., Long Y. Design of free-form lens based on annular uniform facula of LED extended light source. Journal of Wuyi University (Natural Science Edition) 2018;32:12–17. doi: 10.3969/j.issn.1006-7302.2018.03.003. [DOI] [Google Scholar]
- 27.Tsallis C., Stariolo D.A. Generalized simulated annealing. Phys. Stat. Mech. Appl. 1996;233:395–406. doi: 10.1016/S0378-4371(96)00271-3. [DOI] [Google Scholar]
- 28.Busetti F. World Wide Web; 2003. Simulated Annealing Overview.www.geocities.com/francorbusetti/saweb.pdf [Google Scholar]
- 29.Du K.-L., Swamy M. Search and optimization by metaheuristics. Techniques and Algorithms Inspired by Nature. 2016:1–10. doi: 10.1007/978-3-319-41192-7_3. [DOI] [Google Scholar]
- 30.Ma D., Feng Z., Liang R. Tailoring freeform illumination optics in a double-pole coordinate system. Appl. Opt. 2015;54:2395–2399. doi: 10.1364/AO.54.002395. [DOI] [PubMed] [Google Scholar]
- 31.Luo Y., Feng Z., Han Y., Li H. Design of compact and smooth free-form optical system with uniform illuminance for LED source. Opt Express. 2010;18:9055–9063. doi: 10.1364/OE.18.009055. [DOI] [PubMed] [Google Scholar]
- 32.Bortz J., Shatz N. Iterative generalized functional method of nonimaging optical design - art. no. 66700A. Proc. SPIE-Int. Soc. Opt. Eng. 2007:6670. doi: 10.1117/12.731897. [DOI] [Google Scholar]
- 33.Wei S., Ma D., Zhu Z., Fan Z. Least-squares ray mapping method for freeform illumination optics design. Opt Express. 2020;28 doi: 10.1364/OE.385254. [DOI] [PubMed] [Google Scholar]
- 34.Crowther B.G., Koch D.G., Kunick J.M., McGuire J.P., Jr., Harned R., Gontin R.A. SPIE; 2002. A Fly's Eye Condenser System for Uniform Illumination; pp. 302–310. [DOI] [Google Scholar]
- 35.Lv T., Fu D., Chen X., Liu J. Effect of optical intergrator element lenses number and shape on the lighting uniformity of solar simulator. J. Optoelectron. Laser. 2014;25:1849–1853. [Google Scholar]
- 36.Li G., Zhang G., Fu M., Wang P., Dou B., Song W. Design and analysis of square integratorin solar simulator. J. Appl. Opt. 2014;35:48–52. doi: 10.5768/JAO201435.0101010. [DOI] [Google Scholar]
- 37.Tawfik M., Tonnellier X., Sansom C. Light source selection for a solar simulator for thermal applications: A review. Renew. Sustain. Energy Rev. 2018;90:802–813. doi: 10.1016/j.rser.2018.03.059. [DOI] [Google Scholar]
- 38.Yang J., Huang Q., Han Y. Application and Simulation in Fitting Optical Surface with Zernike Polynomial. Spacec. Recov. Remote Sens. 2010;31:49–55. doi: 10.3969/j.issn.1009-8518.2010.05.009. [DOI] [Google Scholar]
- 39.Duan W., Piao M., Quan X., Zeng Y. Design of compact double free-form surface lens with uniform illumination for extended light source. Acta Opt. Sin. 2022;42:161–169. doi: 10.3788/aos202242.1522001. [DOI] [Google Scholar]
- 40.Meuret Y., Vangiel B., Christiaens F., Thienpont H. Efficient illumination in LED-based projection systems using lenslet integrators. Proc. SPIE-Int. Soc. Opt. Eng. 2006;6196:619605–619610. doi: 10.1117/12.661219. [DOI] [Google Scholar]
- 41.Giel V., Bart Using a fly's eye integrator in efficient illumination engines with multiple light-emitting diode light sources. Opt. Eng. 2007;46:043001. doi: 10.1117/1.2727313. [DOI] [Google Scholar]
- 42.Saunders I.J., Ploeg L., Dorrepaal M., Van Venrooij B., Stahl H.P. Fabrication and metrology of freeform aluminum mirrors for the SCUBA-2 instrument. Proc. SPIE-Int. Soc. Opt. Eng. 2005;5869:586905–586912. doi: 10.1117/12.612998. [DOI] [Google Scholar]
- 43.Zhu R., Sun Y., Shen H. Progress and prospect of optical free-form surface measurement. Acta Opt. Sin. 2021;41:161–178. doi: 10.3788/aos202141.0112001. [DOI] [Google Scholar]
- 44.Li R., Zhang Z., Du X., Kong L., Jiang J. Ultra-precision machining technology of free-form optics and its applications. Infrared Laser Eng. 2010;39:110–115. doi: 10.103969/j.issn.1007-2276.2010.01.023. [DOI] [Google Scholar]
- 45.IEC 60904-9:2020 “Photovoltaic Devices - Part 9: Classification of Solar Simulator Characteristics”. 2020. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
-
•
All data reported in this paper will be shared by the lead contact upon request.
-
•
The codes are available on reasonable request from the lead contact.
-
•
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.