Figure 2:

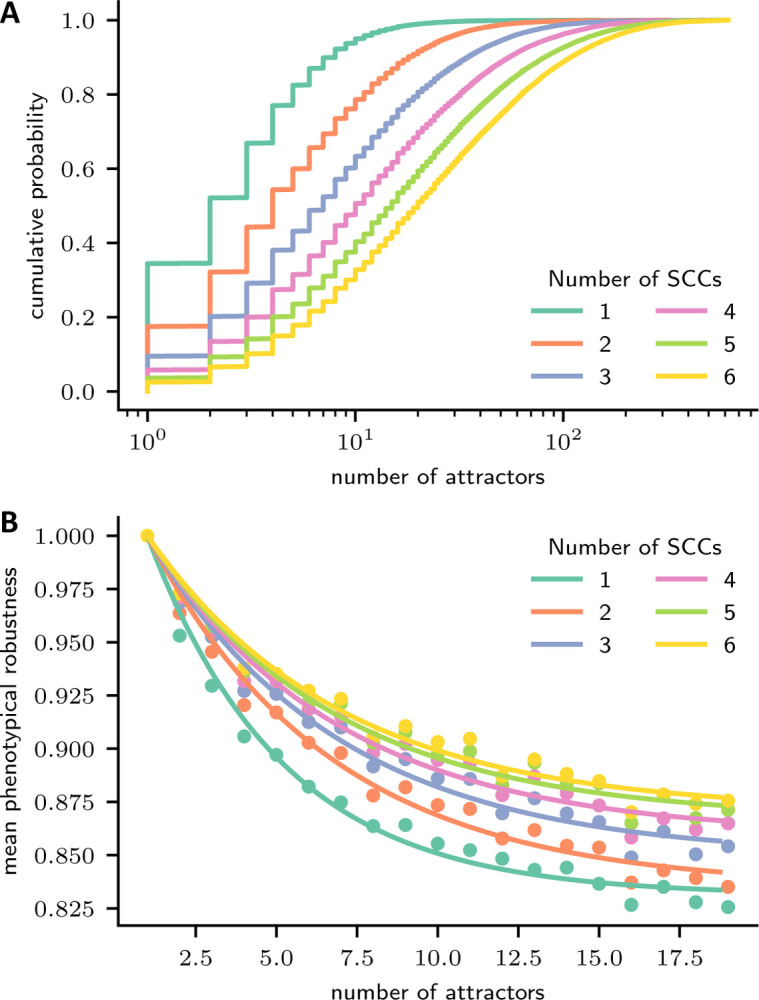
Modularity confers dynamical complexity and phenotypical robustness. 60-node nested canalizing Boolean networks with a constant in-degree of 3 and with 1–6 modules (i.e., SCCs of the wiring diagram) of equal size were generated (50,000 networks each). For each modular network, a weakly connected directed graph describing the connections between modules, as well as a single edge connecting an upstream with a downstream module were selected uniformly at random. By following the transitions of 500 random initial states to their attractors, the phenotypical robustness and a lower bound for the dynamical complexity (here, number of attractors) were established for each network. (A) Cumulative empirical density function of the number of attractors, stratified by the number of modules or SCCs. (B) The mean phenotypical robustness $\left(y\right)$ is plotted against the number of discovered attractors $\left(x\right)$, stratified by the number of modules or SCCs (dots). Since $y\left(1\right)=1$, the two-parameter function $y=\alpha +(1-\alpha )e^{-k(x-1)}$ is fitted to the means of the number of attractors for $x=1,\dots ,19$ (lines).