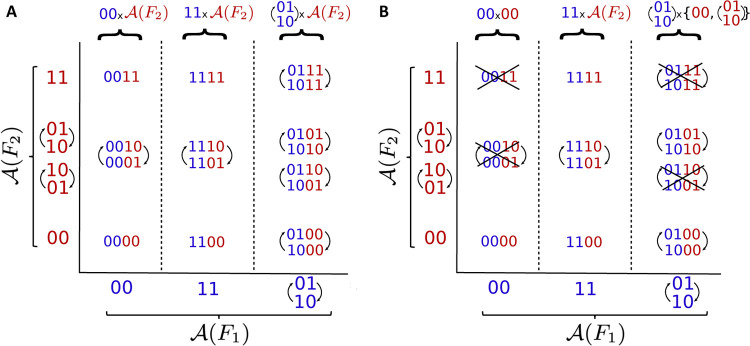
Figure 4:

Attractors of a Cartesian product and a semi-direct product. (A) The space of attractors of a Cartesian product $F=F_1\times F_2$, with $F_1\left(x_1,x_2\right)=\left(x_2,x_1\right),F_2\left(x_3,x_4\right)=\left(x_4,x_3\right)$, can be seen as a Cartesian product of $𝒜\left(F_1\right)$ and $𝒜\left(F_2\right)$. To illustrate the different ways to combine attractors of $F_1$ and $F_2$, in the panel we explicitly write (01,10) and (10,01) for $F_2$. (B) In general, the coupling of networks does not behave as a Cartesian product and the space of attractors depends on this coupling. The crossed-out attractors indicate which attractors from the Cartesian product are lost when using a semi-direct product with coupling scheme $P=\left\{\left(x_3,x_2{x}_4\right)\right\}$, and $F_1,F_2$ as in $\mathrm{A}$.