Orientation and Dynamics of Cu²⁺ Based DNA Label from Force Field Parameterized MD Elucidates the Relationship Between EPR Distance Constraints and DNA Backbone Distances

Abstract

Pulsed electron paramagnetic resonance (EPR) based distance measurements using the recently developed Cu²⁺-DPA label present a promising strategy for measuring DNA backbone distance constraints. Herein we develop force field parameters for Cu²⁺-DPA in order to understand the features of this label at an atomic level. We perform molecular dynamics (MD) simulations using the force field parameters of Cu²⁺-DPA on four different DNA duplexes. The distance between the Cu²⁺ centers, extracted from the 2 μs MD trajectories, agree well with the experimental distance for all the duplexes. Further analyses of the trajectory provide insight into the orientation of the Cu²⁺-DPA inside the duplex that leads to such agreement with experiment. The MD results also illustrate the ability of the Cu²⁺-DPA to report on the DNA backbone distance constraints. Furthermore, measurement of fluctuations of individual residues showed that the flexibility of Cu²⁺-DPA in a DNA depends on the position of the label in the duplex, and a 2 μs MD simulation is not sufficient to fully capture the experimental distribution in some cases. Finally, the MD trajectories were utilized to understand the key aspects of the double electron electron resonance (DEER) results. The lack of orientational selectivity effects of the Cu²⁺-DPA at Q-band frequency are rationalized in terms of fluctuations in the Cu²⁺ coordination environment and rotameric fluctuations of the label linker. Overall, a combination of EPR and MD simulations based on the Cu²⁺-DPA labelling strategy can contribute towards understanding changes in DNA backbone conformations during protein-DNA interactions.

Graphical Abstract

MD simulations highlight how EPR distance constraints from Cu²⁺-DPA labels can be interpreted in terms of DNA structure.

Introduction

The DNA helix has a wide range of sequence dependent conformational variability and internal dynamics that are essential for its role in biological processes^1–5. The DNA helix undergoes breathing, bending and twisting motions, as well as fluctuations in the helical groove that impart flexibility to the helix. Such dynamics are crucial in many important physiological processes. For example, sequence-dependent bending of DNA is an important criterion for protein-DNA recognition and the function of several DNA-binding proteins, such as transcription regulators and restriction enzymes. In recent times, electron paramagnetic resonance (EPR) spectroscopy has increasingly become important for measuring such conformational dynamics in DNA.

In particular, distance measurements by pulsed EPR techniques are an important approach for elucidating macromolecular conformations and flexibility^6,7. These EPR techniques exploit the dipolar coupling between unpaired electron spins to provide distances in the nanometer range with angstrom-level resolution^7–18. Such distance constraints can be employed to probe conformational changes in large and complex systems such as membrane proteins, chaperones, protein-protein and protein-nucleic acid complexes, that are otherwise inaccessible to other biophysical techniques^19–27.

For such measurements site-specific labelling^28–30 of the biomolecule is needed. A wide variety of labels have been developed towards this purpose^31,32. For nucleic acids, the spin labels are incorporated by modification of nucleobase^33–41, backbone^42–45 or terminal capping^46,47. Nitroxide based labels are commonly used in DNA. Labels such as the cytidine analogue or C-spin^48–50 are highly rigid and provide information on label orientations^51–53. More recently, a sterically shielded nitroxide label, known as G-spin label,⁵⁴ has been reported that is introduced post synthetically. The G-spin label binds non-covalently to an abasic site and is present close to the helix. Additionally, distance measurements at physiological temperatures have been made possible by the triarylmethyl (TAM) radical^55,56. Moreover, paramagnetic spin labels such as Mn²⁺, Gd³⁺ and Cu²⁺ have also been used to label nucleic acids^57–60.

One such labelling strategy that has shown promise is a Cu²⁺ chelated to the ligand 2,2’-dipicolylamine (DPA) phosphoramidite⁶¹. The DPA moiety is nucleotide independent and can be easily introduced at any desired positions in the duplex during the synthesis. In addition, the label is structure independent and thus, does not depend on any specific combinations of bases to bind to, such as a guanine quadruplex. The complementary site to the Cu²⁺-DPA in the opposing strand contains an abasic site (dSpacer). We recently reported distance measurements performed on several duplexes that were labelled at two sites with the Cu²⁺-DPA⁶². The experimental most probable distances agreed with the predicted distances using the known values of base pair separation for a B-DNA. Moreover, molecular dynamics (MD) simulations performed on an unlabelled DNA also suggested that the most probable distance measured from the experiment agreed with the corresponding C3’-C3’ or C4’-C4’ backbone distances. These results suggest that the most probable distances obtained using Cu²⁺-DPA labels can be used to report on the DNA backbone conformations in solution⁶².

However, EPR distance measurements provide sparse constraints and therefore, can benefit from complementary technique, such as simulations using force field parameters of the labels to better describe the dynamical behaviour. MD simulations including the spin labels combined with EPR distance constraints have provided valuable information on conformational dynamics of nucleic acids, relative orientation of double-stranded helices and flexibility of DNA for a specific sequence^{53,54,63–65}. Such MD simulations can also provide insight into the global (DNA) and local (spin label) motions. The development of accurate force fields for the spin label is, however, a pre-requisite for such MD simulations.

In this work, we have developed force field parameters for Cu²⁺-DPA and its complementary base, dSpacer. Density functional theory (DFT) calculations were utilized to generate the optimized geometry of Cu²⁺-DPA and the dSpacer. Consequently, parameters of bond lengths, bond angles, dihedral angles, partial charges, and force constants were developed. We then performed MD simulations with these force fields to better understand the atomic details of the flexibility of DNA as well as the label, Cu²⁺-DPA. The simulations were performed on duplexes with base pair separations of 9 to 12 between the Cu²⁺-DPA labels. We ran the MD simulations for as long as 2 μs to sample the label dynamics that occur on much longer timescales. These long simulations provide insight into the shape and width of the experimental distance distributions that were observed in Cu²⁺-DPA labelled DNA^62,66, the experimental methodology used to measure distances by EPR, and the spatial distribution of the Cu²⁺-DPA label in the context of the DNA.

Experimental

HYSCORE

Four-pulse hyperfine sublevel correlation (HYSCORE)⁶⁷ experiments were performed at 20 K and at X-band frequencies. The pulse sequence π/2 – τ – π/2 – t1 – π – t2 – π/2 – τ – echo was used. HYSCORE was performed at the field of highest intensity. The initial time delays for τ, t1 and t2 was set at 128, 200 and 200 ns, respectively. The delay for t1 and t2 had a step size of 16 ns for a total of 256 points. The pulse lengths used were 16 ns and 32 ns for π/2 and π pulses, respectively. A four-step phase cycling was used to eliminate the unwanted echos^68,69. The raw 2D time-domain signals were analysed and processed using the Hyscorean open-source software package⁷⁰ in MATLAB to produce the 2D frequency-domain contour plot.

DFT optimization

The Cu²⁺ is coordinated to three nitrogen atoms of the DPA in the equatorial plane. Therefore, the remaining sites in the Cu²⁺-DPA complex can be occupied by one, two or three water molecules, depending on the geometry. To find out the most possible Cu²⁺-DPA structure, we performed ab initio calculations using a density functional theory (DFT) with the solvent effect being taken into account with the Polarizable Continuum Model implemented in Gaussian 16 software package⁷¹. We first conducted geometry optimizations at the wB97xd/6–311++G(2d,p) level for three possible Cu²⁺-DPA complexes with 1, 2 and 3 coordinated water molecules. The complexation energy of introducing a water molecule to a Cu²⁺DPA complex was then calculated. After the most probable Cu²⁺-DPA complex was identified, we performed vibrational frequency analysis to derive the bond stretching and bond angle bending force constants for the complex at B3LYP/6–31G* level after geometry optimization. Lastly, HF/6–31G* single point calculations were performed to generate electrostatic potentials (ESP) for the Restrained ESP charge fitting. All zero-point energy (ZPE) calculations were performed using the same DFT model as optimization. More information on partial charges, atom types and other force field parameters and residue topologies of the Cu²⁺-DPA are provided in the ESI.

MD simulations

First, the Nucleic Acid Builder (NAB) module in the AMBER software suite⁷² was used to create the unlabelled B-DNA models, with Cu²⁺-DPA and dSpacer positions replaced by adenine and thymine, respectively. The adenine and thymine residues at the specific sites were then replaced by the DFT-optimized structures of Cu²⁺-DPA and dSpacer in PyMOL⁷³. The Cu²⁺-DPA and dSpacer incorporated DNA were then subjected to MD simulations. The AMBER parmbsc1 force field⁶³ was used to treat the nucleic acids. For the modified nucleotide residue, we first developed force field parameters for a model compound as shown in Figure 1, using a strategy detailed previously⁷⁴. The residue topologies and the key force field parameters of Cu²⁺-DPA and dSpacer are provided in ESI. The solvent water was treated with TIP3P water model⁷⁵. The DNA duplexes were solvated in a 12 Å truncated octahedral water box. For each DNA duplex, 100 Cl⁻ ion were added to the water box so that the final Cl⁻ concentration is about 0.15 M and the counter ion Na⁺ were then added to neutralize the whole system. The energy minimization and molecular dynamics simulations were performed using the pmemd program in the AMBER16 software package⁷⁶. The solvated systems were first energy-minimized with a harmonic restraint force applied to the DNA residues except for the Cu²⁺-DPA and dSpacer. The restraint force was gradually reduced from 20, 10, 5, 1 and finally to 0 kcal/(mol Ų). The systems were then gradually heated from 50, 100, 150, 200, 250 to 298.15 K. The systems were equilibrated for 2 ns before starting the production MD runs. The time step for integration for heating, equilibration and the production run were set to 2 fs. Periodic boundary conditions along with particle mesh Ewald (PME)⁷⁷ were applied to account for long-range electrostatic interactions under NPT (P=1 atm) conditions. SHAKE⁷⁸ was used to restrain all bonds involving hydrogen and a nonbonded cutoff of 10 Å was applied. All visualizations for simulations were done using VMD⁷⁹.

Figure 1:

Cu²⁺-DPA-DNA duplex with the Cu²⁺-DPA motif (highlighted by a rectangle) and the dSpacer (highlighted by a circle). The base pair separation between the two Cu²⁺-DPA motifs is denoted by n.

Results and Discussion

In this work we systematically examined four Cu²⁺-DPA-DNA duplexes using MD simulations. Figure 1 shows a Cu²⁺-DPA-DNA duplex with two Cu²⁺-DPA motifs, one on each strand, and a dSpacer, complementary to the Cu²⁺-DPA. The base pair separations (n) between the Cu²⁺-DPA motifs were monotonically increased from 9 to 12. The distance distributions on these duplexes have been reported previously⁶².

DFT optimized structure agrees well with crystal structure

We first identified the most probable structure from three possible Cu²⁺-DPA complexes with 1, 2 or 3 water molecules, using high-level DFT-optimizations at the wB97xd/6–311++G(2d,p) level. The optimized geometries are shown in Figure 2. We observed that Cu²⁺-DPA-WAT₃ is not stable as one Cu-OH₂ distance is 3.988 Å (Figure 2A), and this water molecule is likely a solvent water. The complexation energy of adding one water to Cu²⁺-DPA to form Cu²⁺-DPA-WAT₁ (Figure 2C) is −19.59 kcal/mol and −16.99 kcal/mol after ZPE correction. On the other hand, the energy after adding another water molecule in Cu²⁺-DPA-WAT₂ (Figure 2B) is only −8.06 kcal/mol and −5.86 kcal/mol after ZPE correction. Considering the vaporization energy of water is −9.75 kcal/mol, Cu²⁺-DPA-WAT₂ is unlikely to be formed in aqueous solvent. Thus, the most probable Cu²⁺-DPA structure contains only one water molecule.

Figure 2:

Cu²⁺-DPA structures coordinated with A) three B) two and C) one water molecule.

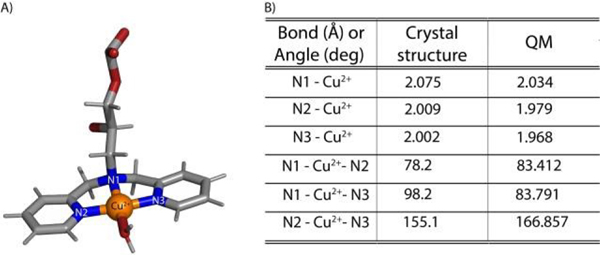
Besides water, the most probable Cu²⁺-DPA complex, as shown in Figure 3A, also has the Cu²⁺ coordinated to three nitrogen atoms of the DPA (N1, N2 and N3), similar to what the crystal structure showed⁸⁰. Previous continuous wave EPR data on Cu²⁺-DPA-DNA^61,62 have reported g_‖ and A_‖ values that were also consistent with three nitrogen coordinating to Cu²⁺ at equatorial positions. On comparing the bond lengths and bond angles between the DFT-optimized and crystal structures, we found a reasonable agreement, as shown in Figure 3B. Furthermore, the optimized geometry did not accommodate any axial water coordination. This absence of axial water coordination indicates a square planar geometry of Cu²⁺-DPA that is in accordance with the crystal structure⁸⁰.

Figure 3:

A) DFT optimized structure of Cu²⁺-DPA B) Comparison of bond angles and bond lengths with crystal structure⁸⁰ of Cu²⁺-DPA show reasonable agreement with the DFT-optimized structure.

HYSCORE indicates the presence of the fourth equatorially coordinating atom

In order to experimentally verify the equatorial water coordination to Cu²⁺-DPA and Cu²⁺-DPA placed in DNA, we performed HYSCORE experiments. Figure 4A shows the ¹H HYSCORE spectrum of Cu²⁺-DPA which displays two proton features. First, the broad ridge spanning a width of 6–9 MHz, highlighted by the rectangles in Figure 4A, is a characteristic feature of solvent coordination in the equatorial plane^81–84. Since three of the equatorial coordination sites of Cu²⁺ are occupied with DPA nitrogen atoms, it leaves space for only one solvent molecule to bind equatorially. Second, the short intense ridge around the proton Larmor frequency (~14 MHz), highlighted by the circle in Figure 4A, can be a consequence of weakly coupled protons of solvent molecules or axial coordination to water⁸². Since crystal structure of Cu²⁺-DPA shows a square planar geometry⁸⁰, the proton feature at ~14 MHz is likely due to the weakly coupled protons of solvent molecules⁸³. We then performed HYSCORE on one of the Cu²⁺-DPA-DNA duplexes (n=11). The HYSCORE spectrum of the Cu²⁺-DPA-DNA duplex, shown in Figure 4B, closely resembles that of the Cu²⁺-DPA, showing both the features of equatorial water coordination and weakly coupled solvent molecules. Furthermore, a Cu²⁺-proton distance of 2.5 Å was estimated from the HYSCORE features (details in ESI). This distance is in good agreement with the 2.4 Å Cu²⁺-proton distance in the DFT-optimized structure.

Figure 4:

¹H HYSCORE spectra of A) Cu²⁺-DPA B) Cu²⁺-DPA-DNA and C) Cu²⁺-control DNA, analysed to the same contour levels. In Cu²⁺-DPA and Cu²⁺-DPA-DNA, the proton signal results from equatorially coordinated water molecule (rectangle) and weakly coupled solvent (circle). In control DNA, the proton signal results from only weakly coupled solvent molecules.

To compare how Cu²⁺ coordination to water differs in the presence and absence of DPA inside the DNA duplex, we performed HYSCORE on a Cu²⁺-bound control DNA, lacking any DPA phosphoramidite or dSpacer. The sequence of the control DNA is the same as the Cu²⁺-DPA-DNA duplex, except the Cu²⁺-DPA and dSpacer positions were replaced by adenine and thymine, respectively. The proton signature in the HYSCORE spectrum, shown in Figure 4C, clearly lacks the features of equatorial water coordination as seen in Cu²⁺-DPA-DNA. Instead, the spectrum only shows the short intense ridge around ~14 MHz. Overall, from the HYSCORE spectra we inferred that the Cu²⁺-DPA is coordinated to a solvent molecule in the equatorial plane, as also observed in the DFT-optimized Cu²⁺-DPA structure.

MD simulations show that the Cu²⁺-Cu²⁺ distance reasonably agrees with the backbone distance

Next, we performed 2 μs MD simulations on the Cu²⁺-DPA and dSpacer incorporated into the DNA duplexes, with n varying from 9 to 12. Figure 5A shows the Cu²⁺-DPA phosphoramidite with the backbone carbon atom, C’ marked in red. The corresponding Cu²⁺-Cu²⁺ and C’-C’ distances in a Cu²⁺-DPA-DNA duplex are shown using solid black and dashed red lines, respectively. We chose C’ as the backbone atom for the Cu²⁺-DPA phosphoramidite as it is the central point to which the DPA moiety is attached. Moreover, the C’ atom best represents the C3’ or C4’ backbone atoms of an unmodified regular nucleotide⁶².

Figure 5:

A) Cu²⁺-DPA phosphoramidite with the backbone carbon atom, C’ marked in red. The Cu²⁺-Cu²⁺ distance is denoted by the black solid line and the backbone C’-C’ distance is represented by the red dashed line in a Cu²⁺-DPA-DNA duplex. The Cu²⁺-Cu²⁺ distance (black solid) is compared with the backbone distance (red dashed) for B) n=9 C) n=10 D) n=11 and E) n=12 base pair separations. F) Plot showing the Cu²⁺-Cu²⁺ and C’-C’ most probable distances from MD simulations.

Figures 5B–E show the comparison between the Cu²⁺-Cu²⁺ and C’-C’ distance distributions obtained from 2 μs trajectories for each DNA duplex. Figure 5F shows a plot of the most probable Cu²⁺-Cu²⁺ and C’-C’ distances from the MD. As can be seen, all the distances agree well within ~2 Å. The plot, therefore, highlights that an important advantage of the Cu²⁺-DPA labelling strategy is that the label can reasonably report on the DNA backbone constraints, without any additional modelling.

The agreement between the Cu²⁺ and backbone C’ distance distributions is due to a combination of three factors. First, the size of the linker is much smaller than standard DNA labels. From the MD simulations, the average length of the Cu²⁺ atom from the C’ backbone atom, ranges from 3.5 to 4.5 Å for the different DPA sites. The linker length in Cu²⁺-DPA is, therefore, considerably smaller than traditional labels, which can be a nanometer long^85,86. Second, the Cu²⁺ is arranged within the helix (cf. below). As a result, the offset due to the linker partially cancels. Finally, the Cu²⁺-Cu²⁺ distance within the DNA helix can be considered as a sum of two components: an axial distance, which increases linearly with the base pair separation and a radial distance (i.e. from backbone to the label), which oscillates with base pair separation. As the two modified sites are separated by at least 9 base pairs, the axial vector (~31 Å for n=9) is significantly longer than the radial counterpart, i.e., the Cu²⁺-Cu²⁺ distance is dominated by the axial component. Indeed, previous work has shown that such considerations are valid for n>4 ⁶². Consequently, the separation between the Cu²⁺ centers along the DNA axis is roughly the same as the separation between the DNA backbone atoms.

Cu²⁺-DPA-DNA based MD simulations capture the experimental most probable distance

Next, we compared the distance distributions obtained from MD simulations to the experimental distance distributions. The experimental data and distance distributions for 9 to 12 base pair separations have been reported previously⁶². The direct comparison of the experimental and MD distance distribution is provided in ESI. Figure 6A shows the comparison of the most probable Cu²⁺-Cu²⁺ distances from the first 1 μs (red triangles) and entire 2 μs (black circles) MD simulations and EPR data (grey squares) for the four Cu²⁺-DPA-DNA duplexes. The distances agree well within 2 Å which is within the error of the experiments⁶². A linear trend with a y-intercept of 0 was obtained with a slope of 3.5 Å, for all the results from the experiment and MD simulations. These values agree well with each other as well as with the ~3.4 Å separation between adjacent bases, as observed in a B-DNA duplex⁸⁷.

Figure 6:

Plot of A) most probable Cu²⁺-Cu²⁺ distances and B) standard deviation of distance distributions from EPR measurements (grey squares), 1 μs MD (red triangles) and 2 μs MD (black circles) against base pair separation (n). A direct comparison of the experimental and MD distance distributions is provided in ESI.

Figure 6B shows the comparison of the standard deviation of the distance distributions obtained from the experimental data (grey squares) and MD simulations (red triangles for 1 μs and black circles for 2 μs). Analysing the initial 1 μs MD trajectories shows a large discrepancy between the experiment and MD for all the duplexes. Extending the simulation time to 2 μs reduces this discrepancy for duplexes n=9, 10 and 12. However, for duplex n=11 there is no improvement with simulation time. This result may indicate that the labels in duplex n=11 have restricted mobility, and therefore limited sampling of rotamers is observed during the 2 μs simulation. This effect is analysed in further detail below. Overall, while longer simulation time may be required to capture the full distribution width, the most probable distance can be achieved with a short simulation time of 1 μs or less (details in ESI).

Orientation of Cu²⁺-DPA helps reduce the effect of linker offset

To elucidate spin label conformations that yield the most probable distance, we extracted the frames from the MD trajectories for which the Cu²⁺-Cu²⁺ distance is within ± 1 Å of the MD most probable distance. The analysis is shown in Figure 7A. Each frame was aligned with respect to the O-C-C’-O backbone atoms, marked in red in Figure 7B. Figures 7C–D show the spatial distribution of Cu²⁺ for the DPA sites corresponding to the most probable distance. As can be seen from Figure 7D, the Cu²⁺ is directed towards the axis of the DNA duplex. This orientation of the Cu²⁺ significantly contributes to the close agreement between the Cu²⁺-Cu²+ and backbone distance distributions (cf. Figure 7D).

Figure 7:

A) The frames from MD trajectories considered for obtaining the spatial distribution of Cu²⁺ are within ± 1 Å of the Cu²⁺-Cu²⁺ most probable distance and shown by the shaded region B) The frames are aligned with respect to the Cu²⁺-DPA backbone atoms marked in red. C) The distribution of the Cu²⁺ centers for the Cu²⁺-DPA site 1 (blue, circles) and site 2 (orange, rectangles) for duplexes n= 9–12. D) The top-down view of the DNA where the blue and orange spheres represent the Cu²⁺ at Cu²⁺-DPA sites 1 and 2, respectively. The grey sphere represents the backbone carbon atom, C’.

In addition, we measured the angle between the DNA backbone and the Cu²⁺ for both the sites in the duplex, as shown in Figure 8A. Figure 8B shows the value of these angles for the different duplexes. Within the standard deviation, the values agree well with each other. Figure 8C shows that the average Cu²⁺ to backbone angles for each duplex are all between 80° to 100°. For a natural base, a similar analysis shows an angle of ~73° ± 6° with respect to the backbone atom (details provided in ESI). Thus, the Cu²⁺-DPA orientation to the DNA backbone is roughly similar to that of a natural base within the standard deviation and within the caveats of structural differences between the label and the natural base. These results suggest that the most probable spin label conformation has the Cu²⁺-ions present almost perpendicular to the DNA backbone. The perpendicular orientation of the Cu²⁺-DPA leads to the effects of linker length to partially cancel out when the Cu²⁺-Cu²⁺ distance is compared to the backbone distance.

Figure 8:

A) Angles between the C4’ atom of the adjacent base to the Cu²⁺-DPA (blue sphere), the C’ backbone atom of Cu²⁺-DPA (grey sphere) and the Cu²⁺ (cyan and orange for Cu²⁺-DPA site 1 and 2, respectively) B) Table showing the values of the angles for the two Cu²⁺-DPA sites C) Plot of the angles versus base pair separation for the two Cu²⁺-DPA sites.

MD simulations show that Cu²⁺-DPA have varied mobility that depends on position

In order to examine the motion of the Cu²⁺-DPA we first measured the root mean square fluctuation (RMSF) values of each base for all the DNA duplexes. The RMSF was calculated with reference to the average structure of each duplex and the results are shown in Figure 9. As expected, the bases at the 5’ and 3’ ends showed high RMSF and thereby, high flexibility. Interestingly, the flexibility of the Cu²⁺-DPA and the dSpacer is also elevated than other bases and are comparable to the nitroxide derivative of guanine⁵⁴. These results are expected because Cu²⁺-DPA and the dSpacer lack intrastrand hydrogen bonding between them unlike regular base pairing. Importantly the difference in RMSF value between DPA and adjacent base is small for n=11. Furthermore, the RMSF values in Figure 9 are consistent with the fluctuations in θ₁ and θ₂ (cf. Figure 8B).

Figure 9:

The root mean square fluctuations (RMSF) of all the bases in the Cu²⁺-DPA-DNA duplexes with A) n=9 B) n=10 C) n=11 and D) n=12. The grey and black denote the two strands in the DNA and the red and blue denote Cu²⁺-DPA and dSpacer, respectively. As can be seen, the RMSF is high for the terminal bases, as expected. The RMSF for Cu²⁺-DPA and the abasic dSpacer positions are generally high, indicating more flexibility than the natural bases.

We analysed the spin label rotameric preferences from the MD trajectories to examine the mobility of the DPA in different sites. The Cu²⁺-DPA moiety is connected to the backbone by two rotatable bonds that are defined here by χ₁ and χ₂. These angles are shown in Figures 10A and 11A, respectively. The χ₁ dihedral angles for both the Cu²⁺-DPA sites in each duplex are shown in Figures 10B–E. In duplexes n=9, 10 and 12, at least one of Cu²⁺-DPA sites sample both ±60° and ±180°, while in n=11 neither of the labels sample the full range. Figures 11B–E show the χ₂ dihedral angles for both the Cu²⁺-DPA sites in each duplex. Overall, a large range of χ₂ values (±60°, ±120° and ±180°) are sampled between the different Cu²⁺-DPA sites of the different duplexes. These observations suggest that the sampling of χ₁ and χ₂ dihedral angles contribute towards the flexibility of the label in a duplex, and that n=11 does not fully sample all rotameric states during the course of MD simulation.

Figure 10:

A) Dihedral angle denoted as χ₁. The probability distribution of the dihedral angles for the two Cu²⁺-DPA labels in duplexes with B) n=9 C) n=10 D) n=11 and E) n=12. Both the Cu²⁺-DPA sites in duplex n=11 sample the least range of χ₁ dihedrals.

Figure 11:

A) Dihedral angle denoted as χ₂. B) Energy landscape for different orientations of Cu²⁺-DPA based on the dihedral angle, χ₂. The probability distribution of the dihedral angles for the two Cu²⁺-DPA labels in duplexes with C) n=9 D) n=10 E) n=11 F) n=12.

Moreover, as evident from Figures 10 and 11, even within the same duplex, two Cu²⁺-DPA sites can have varied mobility. Such differences in the mobility depending on the location of the Cu²⁺-DPA site is not unreasonable given that local steric interactions with the neighbouring bases have a strong influence on the degree of motions of the label.

Finally, these results suggest that a 2 μs simulation may be insufficient, in cases, to fully capture the experimental distribution due to the slow motion of the label^33,88–90. In addition, there may be contribution from other factors that lead to the discrepancy between the distribution widths in MD simulations vs the experiment. The experimental data was collected at 20 K which likely captures the conformations that exist in the glass state, while the simulation was performed at 298 K. Second, glycerol was used in the experiment to form a glass and as a cryoprotectant. It is possible that the presence of glycerol modified the solvation and dynamics of the DNA^91,92.

MD simulations provide insight into the use of DEER for distance measurements

The MD results are also helpful to understand key principles of the double electron electron resonance (DEER) measurements on Cu²⁺-DPA labelled species. The pulses used in DEER excite only a small fraction of the total EPR spectrum. Such selective excitation can lead to selection of only a small portion of all possible molecular orientations, resulting in dependence of the measured signal on the magnetic field. This is often referred to as orientational selectivity^59,93–101. Previous DEER results have shown the absence of orientational effects for Cu²⁺-DPA at both X-band and Q-band frequencies in the non-complexed state^61,62. This is intriguing because Cu²⁺-based measurements on proteins using the dHis motif^{74,93,102–104} can be orientational selective at Q-band but not at X-band.

We examined the MD data to gain insight into these observations. Figure 12 shows the fluctuations of the bond lengths for bonds involving Cu²⁺. These bond lengths were extracted from the 2 μs MD trajectory on the n=11 duplex since previous Q-band data on this sample did not exhibit orientational selectivity⁶². The bond length between Cu²⁺ to N1 ranges from 1.9 to 2.3 Å, with an average bond length of 2.1 ± 0.1 Å (average ± s.d.). On the other hand, the bond length of Cu²⁺ to N2 was 1.9 ± 0.1 Å. These mean values agree well with the crystal structure⁸⁰ (cf. Figure 3). Figure 13 shows the dihedral angles between Cu²⁺ and atoms in its immediate coordination environment. The dihedral angles, labelled as N1, N2 and N3, show values of −75° ± 23°, −20° ± 7° and 19° ± 6° (average ± s.d.) respectively and are similar for the two Cu²⁺-DPA sites. The ensemble measured by DEER is therefore expected to contain proteins trapped in these different coordination environments.

Figure 12:

Fluctuations in bond length between Cu²⁺ and two coordinating nitrogen atoms – A) bond between Cu²⁺ and the backbone N1 atom B) fluctuations in Cu²⁺-N1 bond length in the two DPA sites, sampled over 2 μs of MD for the duplex n=11 (top chart) and the probability distribution (bottom chart) C) and D) same analysis repeated for bond length between Cu²⁺ and the pyridine N2 atom. A change of ~ 25% in the bond length is observed for Cu²⁺-N1 and ~30% for Cu²⁺-N2.

Figure 13:

Dihedral angles measured between Cu²⁺ and its coordinating atoms for 2 μs of MD run on Cu²⁺-DPA-DNA duplex with n=11. The dihedral angle is denoted by the red arrow (top chart). Bottom chart shows the probability distribution of the dihedrals between the two Cu²⁺-DPA sites, Cu²⁺-DPA1 (blue) and Cu²⁺-DPA2 (orange).

Such variations in the coordination environment of Cu²⁺ have significant influence on the g-tensor of the label. Accordingly, we calculated the g-tensor values and orientations for 100 snapshots from our MD using ORCA^105,106. For these calculations, we sampled every 10 ns of the first 1 μs trajectory of duplex n=11. The distribution in g_‖ orientations shows dramatic variations with as much as a 25o change, as shown in cyan in Figure 14. Due to its 180o symmetry^93,97, the g orientations show both ‘up’ and ‘down’ orientations with respect to the plane of the Cu²⁺-DPA moiety. This is not unexpected and has been observed before^93,97. In addition to this distribution of g_‖ in the two Cu²⁺ centers, there is also additional contribution due to the fluctuations of the dihedral angles χ₁ and χ₂ (cf. Figures 10 and 11).

Figure 14:

The distribution of g_‖ directions (cyan) in the Cu²⁺-DPA system, sampled every 10 ns of the 1 μs MD run. The blue and red bonds show the Cu²⁺ coordination with nitrogen and oxygen, respectively. The cyan represents the g_‖. The g-tensor calculations were performed with ORCA^105,106.

Together these two effects have significant implications on the relative orientations of the g-tensors of the two Cu²⁺ spins in the DNA duplex. The relative angles of the two g-tensors are defined by three angles that are shown in Figure 15A. χ is the angle between the g_∥ axis and the interspin vector, r. γ is the angle between the g_∥ axis of spin A and its projection on spin B. η is the angle between the g_⊥ axis of spin A and its projection on spin B.

Figure 15:

A) The relative orientations between the two spins, A and B, are indicated by three angles, χ, γ and η. B) The echo-detected field swept spectrum of Cu²⁺-DPA-DNA duplex with n=11 at Q-band frequency. The red lines show the fields at which DEER was simulated. C) The simulated DEER time traces at each field at the Q-band frequency. The y-axis is offset for ease of visualization. The red dashed line represents the first period of the modulations for all fields. D) Background subtracted time domain data at g_‖ (11220 G, dashed) and g_⊥ (11820 G, solid) regions. The figure shows the lack of orientational selectivity effects at Q-band frequency for Cu²⁺-DPA.

The three angles, namely χ, γ, and η, were calculated via the MDTraj software¹⁰⁷ for 100 snapshots of the Cu²⁺-DPA-DNA duplex with n=11. From our analysis, we obtained an average of 103° ± 69° (average ± s.d.), 87° ± 36° and 93° ± 44° for χ, η and γ, respectively. Similar analysis of angles for the dHis-Cu²⁺ protein label have shown a standard deviation of ~10–12° for each set of angles^74,93. Thus, the Cu²⁺-DPA labels have an orientational distribution that is significantly larger compared to the dHis-Cu²⁺ label used for proteins The key distinguishing feature appears to be the smaller contribution from side-chain fluctuations in the dHis motif^74,93.

We utilized the values of χ, γ, and η angles and performed simulations to obtain individual time-domain DEER signals at various magnetic fields using the methodology reported previously¹⁰⁸. The parameters used for the simulations include the g and hyperfine tensor values for Cu²⁺-DPA (g_‖ = 2.247, g_⊥ = 2.054, A_‖ = 170 G and A_⊥ = 17 G⁶²). We also used the experimental most probable distance of 3.78 nm and a standard deviation of 0.38 nm for the distance distribution for duplex n=11. Figure 15B shows the eight different magnetic fields where we have previously reported DEER for n=11⁶² and where the simulations are carried out in this work. As can be seen from Figure 15C, the simulated DEER time traces have the same period at all fields. Furthermore, Figure 15D shows that there is no difference in the dipolar frequency at the g_⊥ (11820 G) and g_‖ (11220 G) regions, indicating the lack of any orientational selectivity effects at Q-band frequency.

Many orientations are excited even at a single magnetic field

In order to visualize how the effects of orientational selectivity is mitigated, we chose one Cu²⁺ centre as the reference and aligned its g_‖ axis to overlay 100 structures of Cu²⁺-DPA-DNA, evenly sampled from the 1 μs MD simulations. Figure 16 shows the locations of the second Cu²⁺ (orange) and the reference Cu²⁺ center is shown as a black sphere. As is evident from the figure, even at a single magnetic field corresponding to g_‖, there is a large number of molecular orientations that can exist. In general, the finite bandwidth of pump pulse in DEER leads to an excitation of an even wider range of molecular orientations at a particular magnetic field. Such occurrence is a combined consequence of fluctuations in the dihedral angles, χ₁ and χ₂ and in the coordination environment of Cu²⁺ leading to a large distribution in the g-tensor orientations.

Figure 16:

MD frames of Cu²⁺-DPA-DNA duplex (n=11) sampled every 10 ns for the first 1 μs. The black sphere in the center is the reference Cu²⁺. All frames are aligned to the g_‖ axis of the reference Cu²⁺. The second Cu²⁺ position is represented as orange spheres. The g_‖ direction, marked in the figure, is calculated from ORCA^105,106.

Conclusions

In conclusion, we have, for the first time, provided tools for modelling of Cu²⁺-DPA by developing force field parameters. The DFT-optimized structure of the label was in reasonable agreement with the crystal structure. Additionally, the most energy favourable DFT-structure had one equatorial water coordination and was consistent with HYSCORE results on the Cu²⁺-DPA-DNA duplex. We have shown that the distance between the Cu²⁺ centers from the MD simulations can directly report on the DNA backbone distances. In addition, the most probable Cu²⁺-Cu²⁺ distance obtained from the experiment and the MD agree within ~2 Å. Further analyses showed that the Cu²⁺-DPA moiety is positioned inside the DNA helix and oriented roughly perpendicular to the DNA backbone, corresponding to the most probable distance. The motions of the label are slow such that simulation longer than 2 μs may be needed, in cases, to adequately capture the experimental distance distribution. Finally, the MD results illustrated that the fluctuations of the Cu²⁺ coordination environment, together with the linker flexibility, lead to a wide distribution of the relative orientation of the two Cu²⁺ g-tensors. This distribution is large enough to dilute any orientational effects, even at Q-band frequency. Overall, the development of force field parameters for the Cu²⁺ labels will enable the use of MD simulations to better interpret EPR distance constraints in understanding the role of DNA in protein-DNA interactions.