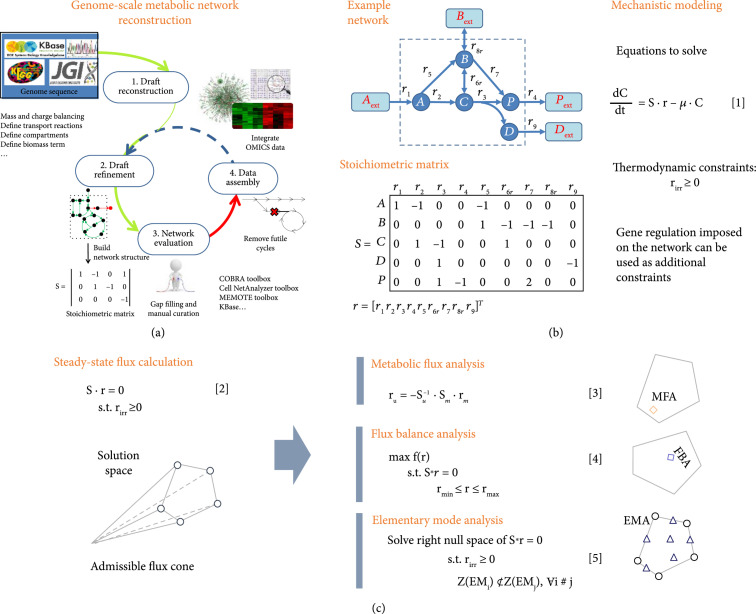
Figure 3.

Mechanistic modeling for plant biosystems design. (a) General steps in reconstructing a genome-scale metabolic network. (b) Mass balance of metabolites in a metabolic network. Equation 1 is a system of ordinary differential equations describing dynamic chemical transformation of metabolites in a metabolic network where $C$ is a metabolite concentration vector, $S$ is a stoichiometric matrix, $r$ is a reaction flux vector, and $\mu$ is the cell growth. (c) Calculation of steady-state flux distributions. Three common methods can be employed to determine metabolic flux distributions including metabolic flux analysis (MFA), flux balance analysis (FBA), and elementary mode analysis (EMA). For a typical metabolic network, a system of homogenous equations [2] is highly underdetermined, resulting in an infinite solution space. MFA determines a physiological state of a cell under a defined condition by calculating $r_u$ based on experimentally measured fluxes $r_m$ that make [2] being determined. Here, $r=\left[r_u{r}_m\right]$, and $S=\left[S_u{S}_m\right]$. FBA also determines a physiological state of a cell by implementing a cellular objective function subject to (s.t.) mass balance and flux bounds. Different from MFA and FBA, EMA unbiasedly seeks to identify all finite admissible fluxes in the solution space by imposing the thermodynamic constraints of reaction direction and pathway nondecomposability. Adapted from [30, 34, 371].