3.Problem Background: In following figure, in isosceles triangle $\Delta ABC$, $AB=AC$, $\angle BAC=120°$, make $AD\perp BC$ at point $D$, then $D$ is the midpoint of $BC$, $\angle BAD=\frac{1}{2}\angle BAC=60°$, so $\frac{BC}{AB}=\frac{2BD}{AB}=\sqrt{3}$.  Application: As in following figure, $\Delta ABC$ and $\Delta ADE$ are isosceles triangles, $\angle BAC=\angle DAE=120°,D,E,C$ points D, E and F on the same line, connecting 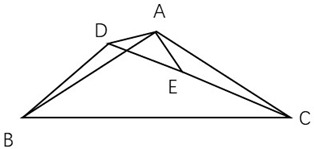$BD$.  (1) How many pairs of equal line segments are there in above figure and point out each of them.  (2) Write an equation of equivalence between the line segments CD, BD, and AD in above figure. (Proof process required)