Accounting for Nonmonotone Missing Data using Inverse Probability Weighting

Abstract

Inverse probability weighting can be used to correct for missing data. New estimators for the weights in the nonmonotone setting were introduced in 2018. These estimators are the unconstrained maximum likelihood estimator (UMLE) and the constrained Bayesian estimator (CBE), an alternative if UMLE fails to converge. In this work we describe and illustrate these estimators, and examine performance in simulation and in an applied example estimating the effect of anemia on spontaneous preterm birth in the Zambia Preterm Birth Prevention Study. We compare performance with multiple imputation (MI) and focus on the setting of an observational study where inverse probability of treatment weights are used to address confounding. In simulation, weighting was less statistically efficient at the smallest sample size and lowest exposure prevalence examined (n=1500, 15% respectively) but in other scenarios statistical performance of weighting and MI was similar. Weighting had improved computational efficiency taking, on average, 0.4 and 0.05 times the time for MI in R and SAS, respectively. UMLE was easy to implement in commonly used software and convergence failure occurred just twice in >200,000 simulated cohorts making implementation of CBE unnecessary. In conclusion, weighting is an alternative to MI for nonmonotone missingness, though MI performed as well as or better in terms of bias and statistical efficiency. Weighting’s superior computational efficiency may be preferred with large sample sizes or when using resampling algorithms. As validity of weighting and MI rely on correct specification of different models, both approaches could be implemented to check agreement of results.

Missing data plague research. Reviews of the epidemiologic and clinical literature show that missing data are often inadequately reported and that complete case analysis, where records with missing data are excluded, remains the most frequently implemented approach to handle missing data.^1–6 Complete case analyses can be statistically inefficient and are valid only under certain assumptions, generally that data are missing completely at random, or that missingness is independent of the outcome and effect modifiers.^7–10 Weighting is an alternative approach to handle missing data that is valid under different assumptions, principally that the data are missing at random.^11–13

It is generally straightforward to estimate weights to account for missing data when missing data follow a uniform pattern (i.e., for each individual, the variables with missingness are either all observed or all missing) or a monotone pattern (i.e., there is an ordering in which a variable is observed only if the previous variable is observed, such as missing data after lost to follow-up) (see illustration in Appendix A).¹² However, until recently, weighting approaches for nonmonotone missing data (i.e., when missingness is neither uniform nor monotone) have been challenging to implement.^14,15 In 2018, Sun and Tchetgen Tchetgen published two estimators for weights in the setting of nonmonotone missingness.^16,17 Unlike prior approaches, their estimators can be readily implemented in commonly used software.

In this paper, we describe and illustrate the estimators from Sun and Tchetgen Tchetgen, and examine their performance in simulation and an applied example estimating the effect of anemia on spontaneous preterm birth in the Zambia Preterm Birth Prevention Study (ZAPPS).^18,19 We compare performance with multiple imputation (MI), a commonly used alternative. We specifically examine the setting of an observational study where inverse probability of treatment weights are used to address confounding. In section 2, we introduce our motivating application. In section 3, we detail our parameter of interest, a sufficient set of identification assumptions, and weighted estimators. In section 4, we describe the weighted estimators from Sun and Tchetgen Tchetgen using a simple example to aid illustration. In section 5, we present results from a limited simulation study to compare performance with MI in finite samples. Section 6 presents results from the motivating application. Finally, in section 7, we discuss the findings and consider the choice between weighting and MI.

2. Motivating application

Our objective was to estimate the effect of maternal anemia on the risk of spontaneous preterm birth among people seeking prenatal care in Lusaka, Zambia. Some research has suggested an association between maternal anemia, particularly when diagnosed early in pregnancy, and poor pregnancy outcomes.^20–22 However, this finding has not been consistently observed.^23,24 To estimate this effect, we used data from ZAPPS,^18,19 an observational prospective cohort of 1450 people recruited at prenatal care initiation in Lusaka, Zambia between 2015 and 2017. A person was eligible if they were ≥18 years old, had a viable intrauterine single or twin pregnancy, presented to prenatal care prior to 20 weeks of gestation if HIV-seropositive or 24 weeks if HIV-seronegative, and resided within Lusaka with no plans to relocate during follow-up. Anemia was diagnosed at enrollment if the capillary hemoglobin concentration was <10.5 g/dL (HemoCue Hb 201).²⁵ Spontaneous preterm birth was defined as delivery occurring after spontaneous labor or membrane rupture prior to 37 weeks of gestation. Additional covariates collected at enrollment and used in this analysis included gestational age at enrollment, maternal age, maternal HIV serostatus, and previous pregnancy and birth history. Three people experienced a miscarriage and were excluded from the analysis, resulting in 1447 people.

Table 1 shows cohort characteristics and occurrence of the outcome, overall and stratified by anemia diagnosis. ZAPPS is typical of many prospective cohorts. Despite rigorous study procedures and active efforts to maximize study retention, some data are missing. In particular, our exposure and outcome have notable missingness; 425 people (29%) did not have a hemoglobin measurement and 239 people (17%) were lost to follow-up. Ignoring missing data, 13.5% of the cohort was anemic and 9.9% had a spontaneous preterm birth. The risk of spontaneous preterm birth was higher among anemic people (12.4%) compared to people without anemia (9.5%) or people with missing anemia status (9.7%). There was also missingness in some covariates: maternal age (n=41, 3%), maternal HIV serostatus (n=3, <1%), and prior stillbirth (n=85, 6%). Table 2 shows the 16 missing data patterns for the 5 variables with missingness. Just over half (781, 54%) of the cohort were complete cases. Among the 666 people with some missing data, 4 patterns accounted for 88%. There were 9 patterns with <1% of the cohort.

Table 1.

Cohort characteristics overall and stratified by anemia status at enrollment

	N (%)
		Anemia status
Characteristic	Overall (N=1447)	Positive (N=138)	Negative (N=884)	Unknown (N=425)
Spontaneous preterm birth	120 (9.9)	15 (12.4)	70 (9.6)	35 (9.7)
Missing	239	17	157	65
At enrollment
Gestational age (weeks)
Median (IQR)	16.1 (13.3, 18.3)	16.9 (14.7, 18.9)	15.9 (12.9, 18.1)	16.6 (13.6, 18.6)
First trimester	432 (29.9)	29 (21)	286 (32.4)	117 (27.5)
Missing	0	0	0	0
Maternal age
Median (IQR)	27 (23, 32)	27 (22, 33)	27 (23, 32)	27 (22, 31)
<20 years	111 (7.9)	11 (8.3)	59 (6.9)	41 (9.8)
20–34 years	1113 (79.2)	102 (76.7)	677 (79.2)	334 (79.9)
≥35 years	182 (12.9)	20 (15)	119 (13.9)	43 (10.3)
Missing	41	5	29	7
HIV+	349 (24.2)	58 (42)	195 (22.1)	96 (22.7)
Missing	3	0	0	3
Nulliparous	457 (31.6)	40 (29)	286 (32.4)	131 (30.8)
Missing	0	0	0	0
Prior preterm birth	410 (28.3)	40 (29)	258 (29.2)	112 (26.4)
Missing	0	0	0	0
Prior stillbirth	126 (9.3)	15 (11.6)	80 (9.6)	31 (7.8)
Missing	85	9	48	28

Abbreviations: IQR, interquartile range

Table 2.

Missing data patterns in the motivating example data from the ZAPPS cohort, n=1447

Pattern	Anemia	Spont. PTB	Maternal Age	HIV serostatus	Prior stillbirth	N	%
1	O	O	O	O	O	781	54.0
2	M	O	O	O	O	330	22.8
3	O	M	O	O	O	151	10.4
4	M	M	O	O	O	58	4.0
5	O	O	O	O	M	45	3.1
6	M	O	O	O	M	26	1.8
7	O	O	M	O	O	21	1.5
8	O	M	M	O	O	12	0.8
9	O	M	O	O	M	11	0.8
10	M	M	M	O	O	5	0.4
11	M	O	O	M	O	2	0.1
12	O	O	M	O	M	1	0.1
13	M	O	M	O	O	1	0.1
14	M	O	M	O	M	1	0.1
15	M	M	O	O	M	1	0.1
16	M	M	O	M	O	1	0.1

“O” indicates variable is observed and “M” indicates variable is missing

Variables not included here (gestational age at enrollment, maternal HIV serostatus, nulliparity, and prior preterm birth) did not have missingness

Abbreviations: Spont. PTB, spontaneous preterm birth

3. Parameter, identification, and weighted estimators

Parameter

Our parameter is the sample average causal effect of a time-fixed binary exposure on the outcome risk, quantified by the risk difference, $\theta =E\left(Y^{x=1}\right)-E\left(Y^{x=0}\right)$, where $Y^x$ is the potential outcome when exposure $X$ is set to $x$. This parameter requires identification of two sample average risks, $E\left(Y^x\right)$, one under exposure ($x=1$) and one under no exposure ($x=0$). We focus on identification of the risk in the observational setting in which there are common causes of the exposure and outcome, $Z$, that produce confounding bias such that the risk is not identified by the crude conditional risk, i.e., $E\left[Y^x\right]\ne E\left[Y\right|X=x]$, even in the absence of missing data.

No missing data

We can point-identify the risk under the assumptions of conditional exchangeability with positivity, causal consistency, and no measurement error. Conditional exchangeability means that, conditional on a set of measured confounders, the potential outcomes are independent of the observed exposure,$Y^x\coprod X|Z$, such that $E\left[Y^x|Z\right]=E\left[Y^x\right|X=x,Z]$.^26,27 Positivity means that every person has a non-zero probability of having each level of exposure across the distribution of $Z$.^26–28 Causal consistency means that the potential outcome $Y^x$ is the observed outcome $Y$ for people with observed exposure $x$.^27,29 With these conditions, $E\left(Y^x\right)$ is identified by a weighted risk where the weight is the inverse of the confounder-conditional probability of exposure (i.e., inverse probability of treatment weight, hereinafter treatment weight), formally

$$E\left[Y^x\right]=E\left[\frac{YI(X=x)}{\mathrm{Pr}\left(X=x|Z=z\right)}\right],$$

where $I\left(a\right)$ is an indicator that takes the value 1 when $a$ is true and 0 otherwise (proof³⁰ in Appendix B) and ${\mathrm{Pr}\left(X=x|Z=z\right)}^{-1}$ is the treatment weight. An estimator of this weighted risk is $\frac{1}{n}{\sum }_i\frac{Y_{i}I(X_i=x)}{\widehat{\mathrm{P}\mathrm{r}}(X_i=x|Z_i)}$ where $i$ indexes the independent and identically distributed $n$ people included in the sample. $\mathrm{Pr}\left(X_i=x|Z_i\right)$ can be estimated nonparametrically or using a parametric model, commonly a logistic regression, called a propensity score model.

With missing data

When some data are missing, the identification conditions described above are not sufficient because the weighted risk above is no longer expressed in terms of fully observed data. Let $R=1$ for complete cases. We can point-identify the risk among the complete cases by incorporating a second weight, formally

$$\begin{gathered} E\left[\frac{Y\mathrm{I}\left(X=x\right)}{\mathrm{Pr}\left(X=x|Z=Z\right)}\right]=E\left[\frac{\mathrm{Pr}\left(R=1|Z=z,X=x,Y=y\right)}{\mathrm{Pr}\left(R=1|Z=z,X=x,Y=y\right)}\frac{Y\mathrm{I}(X=x)}{\mathrm{Pr}\left(X=x|Z=Z\right)}\right] \\ =E\left[\frac{E[I(R=1)|Z=z,X=x,Y=y]Y\mathrm{I}(X=x)}{\mathrm{Pr}\left(R=1|Z=z,X=x,Y=y\right)\mathrm{Pr}\left(X=x|Z=z\right)}\right] \\ =E\left[\frac{Y\mathrm{I}(X=x)\mathrm{I}(R=1)}{\mathrm{Pr}\left(R=1|Z=z,X=x,Y=y\right)\mathrm{Pr}\left(X=x|Z=z\right)}\right]. \end{gathered}$$

The first equality is multiplication by 1, the second is the equivalence between probability and expectation of an indicator function, and the third is the law of total probability. The additional weight, ${\mathrm{Pr}\left(R=1|Z=z,X=x,Y=y\right)}^{-1}$, is the inverse of the conditional-probability of missingness, hereinafter the missingness weight. We require additional conditions to obtain $\mathrm{Pr}\left(R=1|Z=z,X=x,Y=y\right)$ because some data on $Z,X$, or $Y$ are not observed for people with $R\ne 1$. These conditions are that the data are missing at random (MAR) and there is positivity. We reserve full explanation of MAR and estimation of $\mathrm{Pr}\left(R=1|Z=z,X=x,Y=y\right)$ for section 4. In the missing data setting, positivity means that everyone has a non-zero probability of being a complete case.^16,17 Once we obtain the missingness weight, we subsequently obtain the treatment weight among the weighted complete cases (proof in Appendix C).³¹ An estimator of the weighted risk is

$$\frac{1}{n_{wt}}{\sum }_i\frac{Y_{i}I(X_i=x,R_i=1)}{\widehat{\mathrm{P}\mathrm{r}}\left(R_i=1|Z_i=z,X_i=x,Y_i=y\right)\widehat{\mathrm{P}\mathrm{r}}(X_i=x|Z_i=z)},$$

where $n_{wt}={\sum }_i\frac{I(X_i=x,R_i=1)}{\widehat{\mathrm{P}\mathrm{r}}\left(R_i=1|Z_i=z,X_i=x,Y_i=y\right)\widehat{\mathrm{P}\mathrm{r}}(X_i=x|Z_i=z)}$.

4. Sun and Tchetgen Tchetgen estimators for the missingness weight

To aide illustration, we introduce a simple example with exposure $X$, outcome $Y$ and confounder $Z$. There are nonmonotone missing data with four patterns (Table 3). Let $R$ denote the pattern to which a person belongs where $R=1$ is reserved for complete cases. For the missingness weight, we require the conditional probability of being a complete case, $P(R=1|Z=z,X=x,Y=y)$, which is the complement of the sum of the probabilities of the other patterns,

$$P\left(R=1|Z,X,Y\right)=1-P\left(R=2|Z,X,Y\right)-P\left(R=3|Z,X,Y\right)-P\left(R=4|Z,X,Y\right)$$

The MAR condition is that missingness is independent of the missing data, conditional on the observed data. For example, $Y$ is missing in pattern $R=2$. Under MAR, $I(R=2)\coprod Y|Z,X$, such that $P\left(R=2|Z,X,Y\right)=P(R=2|Z,X)$. Applying this condition to each pattern, we get

$$\mathrm{Pr}\left(R=1|Z,X,Y\right)=1-\mathrm{Pr}\left(R=2|Z,X\right)-\mathrm{Pr}\left(R=3|X\right)-\mathrm{Pr}\left(R=4|X,Y\right).$$

When missingness is not independent from the missing data, neither marginally nor conditional on observed data, then data are missing not at random (MNAR). Data are missing completely at random (MCAR) when missingness is marginally independent of the observed and missing data, a stronger condition than MAR.

Table 3.

Missing data patterns in the simple illustrative example

Pattern (R)	Z	X	Y
1	O	O	O
2	O	O	M
3	M	O	M
4	M	O	O

“O” indicates variable is observed and “M” indicates variable is missing

Sun and Tchetgen Tchetgen developed two estimators for the conditional probability of being a complete case under MAR.^16,17 Let ${\pi }_r$ be the probability for each pattern. We specify logistic models for each pattern $R>1$, formally

$$\mathrm{Pr}\left(R=2|Z,X\right)={\pi }_2({\gamma }_2)=1/(1+\mathrm{e}\mathrm{x}\mathrm{p}(-({\gamma }_{20}+{\gamma }_{21}X+{\gamma }_{22}Z)))$$

$$\mathrm{Pr}\left(R=3|X\right)={\pi }_3\left({\gamma }_3\right)=1/(1+\mathrm{e}\mathrm{x}\mathrm{p}(-({\gamma }_{30}+{\gamma }_{31}X)))$$

$$\mathrm{Pr}\left(R=4|X,Y\right)={\pi }_4\left({\gamma }_4\right)=1/(1+\mathrm{e}\mathrm{x}\mathrm{p}(-({\gamma }_{40}+{\gamma }_{41}X+{\gamma }_{42}Y))).$$

The first estimator is the unconstrained maximum likelihood estimator (UMLE). We maximize the joint log-likelihood of the models using the observed data,

$$\ln ℒ\left(\mathrm{\gamma }\right)=\sum _{i=1}^n\left\{\left[\sum _{r=2}^{4}I\left(R_i=r\right)\ln {\pi }_r\left({\gamma }_r\right)\right]+I\left(R_i=1\right)\ln \left[1-\sum _{r=2}^4{\pi }_r\left({\gamma }_r\right)\right]\right\}.$$

Each person contributes a term to the likelihood that corresponds to the pattern to which they belong. The log-likelihood can be maximized in standard software and we provide code in SAS (using the NLMIXED procedure) and R (using nlm in the Stats package)³² (available at https://github.com/rachael-k-ross/Wgt-NonmonotoneMiss). The UMLE does not naturally impose the constraint that ${\pi }_1>0$, so the log-likelihood may fail to converge if there is a fitted ${\pi }_1$ for a complete case close to zero. Therefore, Sun and Tchetgen Tchetgen also proposed the constrained Bayesian estimator (CBE).

The CBE bounds the probability of being a complete case away from zero by discarding draws from the posterior that do not meet a user-specified constraint. Let $c$ be a user-specified constraint that is a small positive number. CBE produces a posterior distribution that is proportional to the combination of the likelihood, constraint, and prior distributions $f\left(\gamma \right)$,

$$f\left(\gamma |X,Z,Y\right)\propto ℒ\left(\gamma \right)I\left(R_i=1\right)I\left({\pi }_2\left({\gamma }_2\right)+{\pi }_3\left({\gamma }_3\right)+{\pi }_4\left({\gamma }_4\right)<1-c\right)f\left(\gamma \right).$$

Sun and Tchetgen Tchetgen used independent diffuse priors for each $\gamma$ parameter, $\gamma ~N(\mathrm{0,100})$ (i.e., multivariate normal with an identity covariance matrix), $c={10}^{-8}$ and adaptive Gibbs sampling to sample from the posterior.³³ They used the median of the posterior samples to estimate $\widehat{\gamma }$. ST provided OpenBugs code for implementation.³⁴ On GitHub (https://github.com/rachael-k-ross/Wgt-NonmonotoneMiss), we provide R code using R2jags package³⁵ which calls Just Another Gibbs Sampler (JAGS).³⁶ The OpenBugs and R2jags code are opaque, so we provide code in SAS and R for a more transparent (though less efficient) manually coded Metropolis-Hastings algorithm with rejection sampling that imposes the user-specified constraint by rejecting draws that violate it.³⁷ Once $\widehat{\gamma }$ are estimated by UMLE or CBE, the missingness weight can be estimated for each complete case.

Inference

The naïve standard error estimate from the weighted analyses described above (incorporating treatment weights or missingness weights, alone or together) is not consistent and resulting Wald-type confidence intervals (CI) may have poor coverage.³⁸ Two options for estimating the standard error and obtaining appropriate CIs are 1) nonparametric bootstrap and 2) the sandwich variance estimator. The sandwich variance estimator can incorporate estimation of all parameters (including the nuisance parameters $\gamma$) or only the parameters of interest, treating the nuisance parameters as known (i.e., not estimated). This latter approach is commonly called the “robust” (Huber-White) sandwich estimator and is expected to produce conservative estimates leading to over-coverage in CIs.^39,40 In contrast, nonparametric bootstrapping will produce nominal CIs though it can be computationally intensive.^41,42 Here we use the robust sandwich estimator.

5. Simulation

We conducted a limited simulation study to assess finite-sample performance of weighting for nonmonotone missingness. The design was guided by the motivating application. We used both SAS and R.

Data generation

We simulated 5000 studies each with $n$ independent individuals, a binary exposure $X$, a binary outcome $Y$, and 3 correlated confounders $\mathit{Z}$ (one continuous and two binary). Under no exposure ($X=0$), the marginal incidence of the outcome was 10%. See Appendix D for data generation details and causal diagram. We varied $n=(1500,5000)$, marginal prevalence of exposure $p_x=(15\%,50\%)$, and the true risk difference, in percentage points, $\theta =(\mathrm{0,5})$.

After generating the full data, we induced missingness guided by our motivating example. In the primary scenario, we generated missing data with 6 patterns and 50% complete cases (Table 4). For each pattern where $R>1$, we specified a logistic model

$$\mathrm{Pr}\left(R=r|Z,X,Y\right)=1/\left(1+\exp \left(-\left({\gamma }_{r0}+{\gamma }_{r1}X+{\gamma }_{r2}Y+{\gamma }_{r3}{Z}_1+{\gamma }_{r4}{Z}_2+{\gamma }_{r5}{Z}_3\right)\right)\right)$$

to obtain individual probabilities of being in that pattern. The probability of being a complete case was the complement of the sum of the other probabilities. The observed missing data pattern, $R$, was generated from a multinomial distribution and then missing data were imposed according to the observed pattern (i.e., value of any variable missing under that pattern was set to missing). We varied the $\gamma$ coefficients to produce missing data that were MAR (coefficients for variables missing in that pattern were zero), MCAR (all coefficients were zero), and MNAR (some coefficients for missing variables were non-zero). The $\gamma$ intercepts were set by numerical approximation to achieve the desired prevalence of each pattern.⁴³ We also explored how the percent of complete cases and number of patterns affected results when data are MAR (secondary scenarios, Table 4).

Table 4.

Missing data patterns in the simulation study

						% in each pattern
Pattern (R)	X	Y	Z 1	Z 2	Z 3	Primary	Secondary scenarios
1	O	O	O	O	O	50	65	35	50	65	35
2	M	O	O	O	O	15	10	15	10	5	15
3	O	M	O	O	O	15	10	15	10	5	10
4	M	M	O	O	O	10	5	15	10	5	10
5	O	O	O	O	M	5	5	10	5	5	10
6	M	O	O	O	M	5	5	10	5	5	10
7	O	O	M	O	O				5	5	5
8	O	M	M	O	O				5	5	5

“O” indicates variable is observed and “M” indicates variable is missing

Analysis

In each simulated cohort, we implemented three approaches to address missing data. Regardless of missing data approach used, we used inverse probability of treatment weighting to address confounding and fit a weighted linear-binomial outcome model conditional on exposure ($E(Y)=\lambda +\theta X$) using generalized estimating equations with an independence covariance structure to estimate the risk difference, $\theta$, and robust standard error for Wald-type 95% CIs.

First, we conducted an analysis restricted to complete cases (i.e., conditional on $R=1$). We fit the treatment propensity score model among the complete cases and estimated the treatment weight as $\widehat{\mathrm{Pr}}{\left(X=x|Z=z,R=1\right)}^{-1}$.

Second, we implemented weighting for missingness. We implemented UMLE and, if UMLE failed to converge, we estimated $\widehat{\gamma }$ as the posterior median obtained by CBE implemented by adaptive Gibbs sampling with a single chain of 10,000 iterations with 5,000 burn-in samples discarded. We used diffuse priors $\gamma ~N(\mathrm{0,100})$ and set $c={10}^{-8}$. For each missingness model, all variables observed in that pattern were included. Models were correctly specified except in MNAR scenarios. Using $\widehat{\gamma }$, we estimated the missingness weight, $\widehat{\mathrm{Pr}}{\left(R=1|Z=z,X=x,Y=y\right)}^{-1}$. We subsequently fit the missingness-weighted treatment propensity score model among the complete cases to obtain the treatment weight, $\widehat{\mathrm{Pr}}{\left(X=x|Z=z\right)}^{-1}$. The final weight was the product of the missingness weight and treatment weight.

Third, we implemented MI by chained equations.^44,45 Using logistic regression for binary variables and linear regression for continuous variables, we imputed missing data 20 times (mice package in R⁴⁶ and MI procedure in SAS). All variables were included in each imputation model; a linear and quadratic term was included for the continuous confounder. In each imputed dataset, we fit the treatment propensity score model and estimated the treatment weight, $\widehat{\mathrm{Pr}}{\left(X=x|Z=z\right)}^{-1}$. From the treatment-weighted outcome models, the 20 estimates were combined by Rubin’s rule,⁴⁷ ($\stackrel{-}{\theta }=\frac{1}{20}\sum _{k=1}^{20}{\widehat{\theta }}_k$ where ${\widehat{\theta }}_k$ is the estimated risk difference from imputation $k$; $V(\stackrel{-}{\theta })=\frac{1}{20}\sum _{k=1}^{20}\widehat{V}({\widehat{\theta }}_k)+\left(1+\frac{1}{20}\right)\left(\frac{1}{20-1}\right)\sum _{k=1}^{20}{{(\widehat{\theta }}_k-\stackrel{-}{\theta })}^2$ where $\widehat{V}({\widehat{\theta }}_k)$ is the estimated robust variance for ${\widehat{\theta }}_k$ in imputation $k$).

Finally, we analyzed the full data without inducing missingness. While not available in practice, the full data provide a reference against which we compare the three approaches. We fit the treatment propensity score model in the full data and estimated the treatment weight as $\widehat{\mathrm{Pr}}{\left(X=x|Z=z\right)}^{-1}$.

To compare estimator performance, we estimated 1) number of times the estimator failed to produce results, 2) bias (mean of the risk difference estimates minus the true risk difference), 3) empirical standard error (standard deviation of the estimates), 4) root mean squared error (square root of the average of the squared differences between each risk difference estimate and the true risk difference), 5) average model standard error (square root of the average of the variance estimates), and 6) CI coverage (proportion of estimated 95% CIs that included the true risk difference).⁴⁸ Failures did not contribute to the estimation of the other performance measures. We also captured the run time as the average time in seconds for a single cohort (each scenario was run separately on a single 2.5GHz processor with up to 15GB of memory allocated; versions R 4.1.0 and SAS 9.4).

Results

Failure to produce results

For all approaches, failures were rare and occurred with similar frequency across the missing data approaches (Table 5). In the primary scenario, failures only occurred when exposure prevalence was 15%, sample size was 1500, and data were missing MAR (≤0.5% failures) or MNAR (≤4.0%). In the primary scenario, there were no failures at the larger sample size, 50% exposure prevalence, or when data were MCAR. In general, failures for weighting and complete analysis occurred when the weighted outcome model restricted to the complete cases did not converge due to too few exposed individuals or too few outcomes. Weighting can also fail if UMLE fails to converge and thus missingness weights are not estimate, however this UMLE non-convergence never occurred in SAS and occurred just twice in R (across 5000 cohorts in 44 scenarios). In those 2 instances, CBE successfully estimated the weights. For the remainder of the simulation results, only UMLE is presented for weighting.

Table 5.

Failures in 5000 simulated datasets when exposure prevalence was 15% and sample size was 1500 for primary missing data scenario (6 patterns, 50% complete cases)

	Risk difference 0%		Risk difference 5%
Missing data approacha	R	SAS	R	SAS
MAR
CC	12 (0.2%)	25 (0.5%)	0 (0.0%)	1 (<0.1%)
MI	18 (0.4%)	25 (0.5%)	0 (0.0%)	1 (<0.1%)
Weightingb	12 (0.2%)	25 (0.5%)	0 (0.0%)	1 (<0.1%)
MNAR
CC	165 (3.3%)	202 (4.0%)	32 (0.6%)	52 (1.0%)
MI	163 (3.3%)	168 (3.4%)	22 (0.4%)	38 (0.8%)
Weightingb	162 (3.2%)	202 (4.0%)	34 (0.7%)	52 (1.0%)

Abbreviations: MAR, missing at random; CC, complete case analysis; MI, multiple imputation; MNAR, missing not at random

^aAll approaches addressed confounding using inverse probability of treatment weights

^bUMLE used to estimate the missingness weights

Statistical performance

Results from R and SAS were approximately equivalent; we present R only. For the primary scenario (6 patterns, 50% complete cases), results are presented in Table 6 and Figure 1 (MAR), Appendix Table 1 and Appendix Figure 1 (MCAR), and Appendix Table 2 and Appendix Figure 2 (MNAR). When data were MAR, complete case analysis was notably biased and thus had poor coverage. At 50% exposure prevalence, MI and weighting performed similarly with negligible bias and nearly the same RMSE and coverage. At 15% exposure prevalence with n=1500, weighting performance declined with a small increase in bias and reduced precision and coverage. Comparably, MI had greater precision and thus lower RMSE. When data were MCAR, bias was negligible for all approaches. Weighting had the same precision as complete case analysis. Again, improved precision of MI over weighting was apparent only at 15% exposure prevalence with n=1500. When data were MNAR, all missing data approaches were biased. At 15% exposure prevalence, weighting had more bias than MI though at 50% exposure prevalence bias was similar.

Table 6.

Bias, empirical standard error, root mean squared error, average model standard error, and 95% confidence interval coverage of the risk difference (in percentage points) for primary missing data scenario (6 patterns, 50% complete cases) when data are missing at random (MAR)

	Exposure prevalence 15%					Exposure prevalence 50%
Missing data approacha	Bias	ESE	RMSE	avg. ModSE	95% CI Coverage	Bias	ESE	RMSE	avg. ModSE	95% CI Coverage
Risk difference 0
n=1500
Full	−0.1	2.2	2.2	2.2	94%	0.0	1.6	1.6	1.6	96%
CCb	−1.6	2.8	3.2	2.8	81%	−1.1	1.9	2.2	1.9	91%
MIb	0.4	4.0	4.1	4.3	94%	0.0	2.6	2.6	2.6	94%
Weightingb,c	−0.5	4.4	4.5	4.5	90%	0.0	2.7	2.7	2.7	95%
n=5000
Full	0.0	1.2	1.2	1.2	95%	0.0	0.9	0.9	0.9	95%
CC	−1.6	1.5	2.2	1.5	77%	−1.0	1.0	1.4	1.0	84%
MI	0.2	2.3	2.3	2.4	94%	0.1	1.4	1.4	1.4	95%
Weightingc	−0.2	2.4	2.4	2.5	94%	0.1	1.4	1.4	1.5	96%
Risk difference 0.05
n=1500
Full	−0.1	2.6	2.6	2.6	95%	0.0	1.7	1.7	1.8	95%
CC	−3.4	3.5	4.9	3.5	74%	−2.5	2.1	3.3	2.2	78%
MI	0.0	4.7	4.7	4.8	94%	0.0	2.8	2.8	2.8	94%
Weightingc	−0.6	5.2	5.2	5.3	91%	0.0	2.8	2.8	3.0	96%
n=5000
Full	0.0	1.4	1.4	1.4	95%	0.0	1.0	1.0	1.0	95%
CC	−3.4	1.9	3.8	1.9	55%	−2.5	1.2	2.7	1.2	45%
MI	−0.1	2.6	2.6	2.6	94%	0.1	1.5	1.5	1.5	95%
Weightingc	−0.1	2.8	2.8	2.9	95%	0.1	1.5	1.5	1.6	96%

Abbreviations: CC, complete case analysis; MI, multiple imputation; ESE, empirical standard error; RMSE, root mean squared error; avg. ModSE, average model standard error; CI, confidence interval

^aAll approaches addressed confounding using inverse probability of treatment weights Results from 5000 simulated cohorts except approaches marked with

^bat 15% prevalence (see Table 5 for number of failures)

^cUMLE used to estimate the missingness weights

Figure 1.

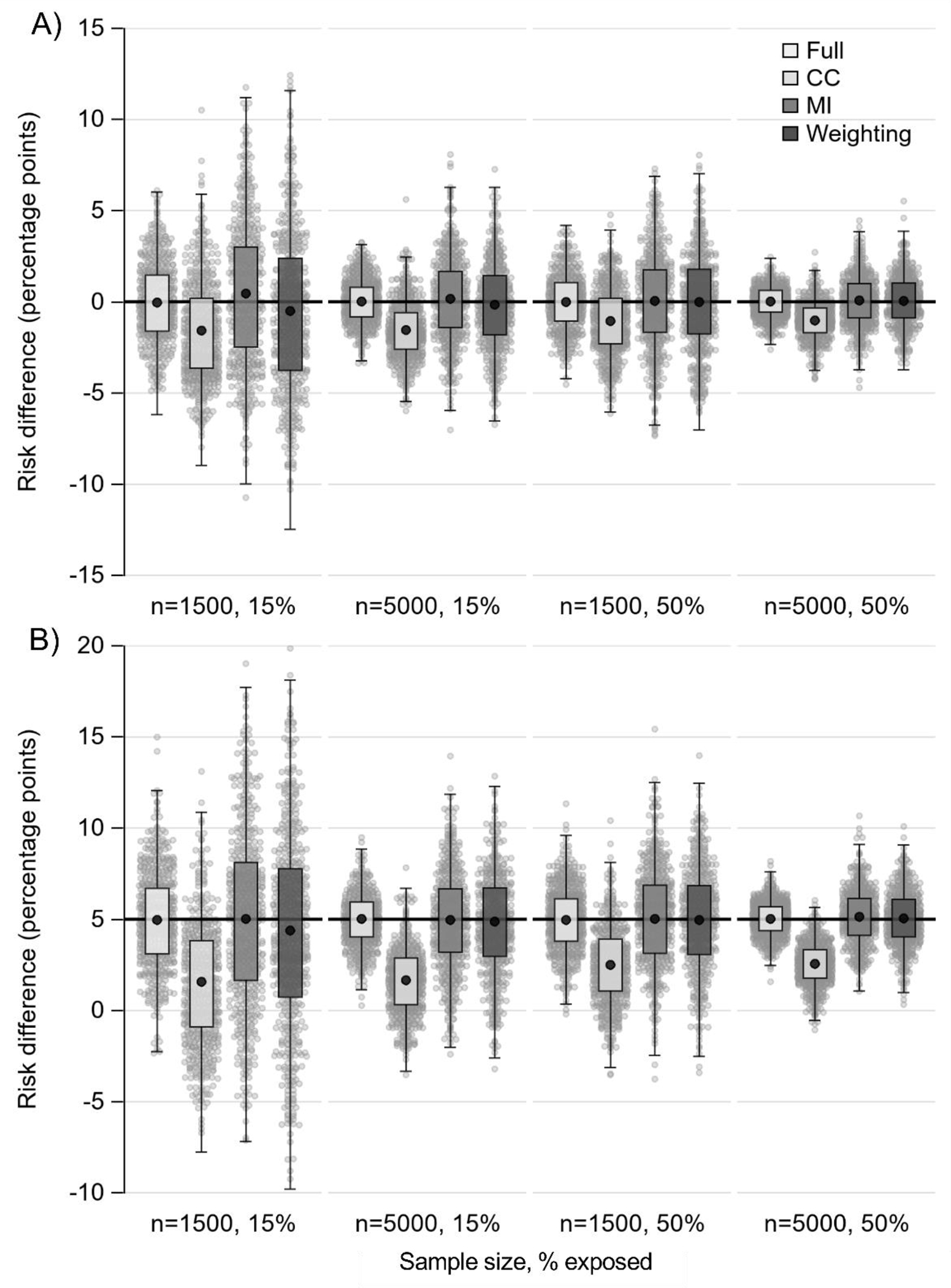
Boxplots of risk difference estimates for primary missing data scenario (6 patterns, 50% complete cases) when data are missing at random (MAR). Panel A) true risk difference is 0%; panel B) true risk difference is 5%. Horizontal black line marks true risk difference; black dot marks mean; small gray dots are a 10% random sample of estimates. Abbreviations: CC, complete case analysis; MI, multiple imputation

Results from scenarios varying percent of complete cases and number of missing data patterns are presented in Appendix Tables 3 and 4. Data were MAR with 50% exposure prevalence. Bias was negligible for MI and weighting so plots of results (Figure 2 and Appendix Figure 3) focus on RMSE and coverage. At n=1500, MI had a lower RMSE than weighting when there were 35% complete cases. A small difference persisted at 50% complete cases only when there were 8 patterns and the difference nearly disappeared at 65% complete cases. A similar pattern was present when n=5000 though the differences between MI and weighting were smaller. For both sample sizes, there was decreasing coverage for MI (dropping <95%) and increasing coverage for weighting (>95%) as the percent of complete cases declines. There were little differences in results when there were 6 or 8 patterns.

Figure 2.

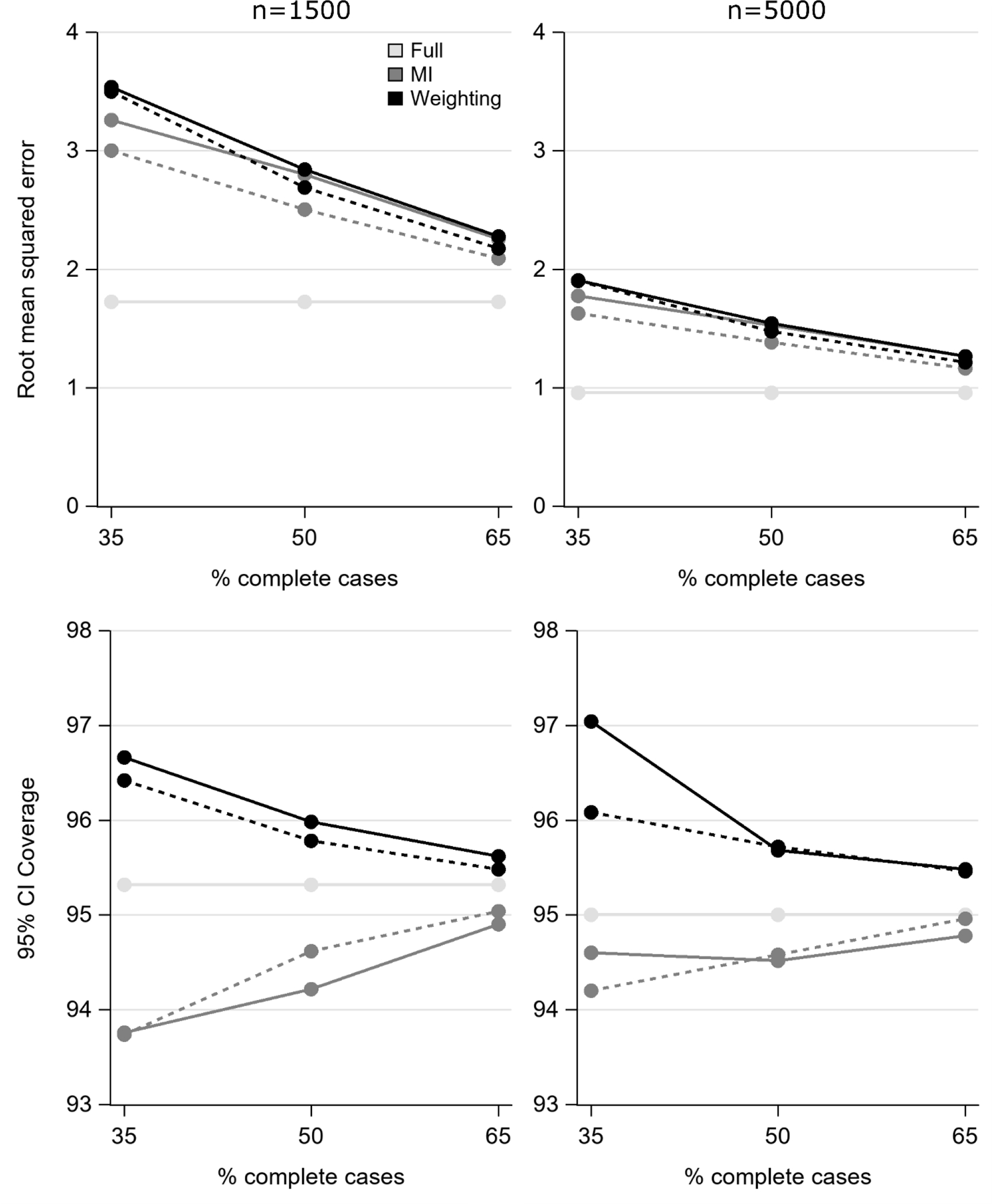
Root mean squared error and confidence interval coverage as percent complete cases and number of patterns varies when the true risk difference is 5% and data are missing at random (MAR). Solid line indicates 6 patterns and dashed line indicates 8 patterns (for Full, the two lines are exactly overlaid). Abbreviations: MI, multiple imputation; CI, confidence interval

Computational efficiency

Figure 3 plots the time in seconds for MI and weighting for all 22 scenarios by sample size (Appendix Table 5 for numeric results). On average, MI took 2.7 times as long as weighting in R (13.0 vs. 4.9 seconds) and 18.3 times as long in SAS (19.2 vs. 1.0 seconds). Weighting was faster in SAS than in R (average 1.0 vs. 4.9); MI was slower in SAS than in R (average 19.2 vs.13.0).

Figure 3.

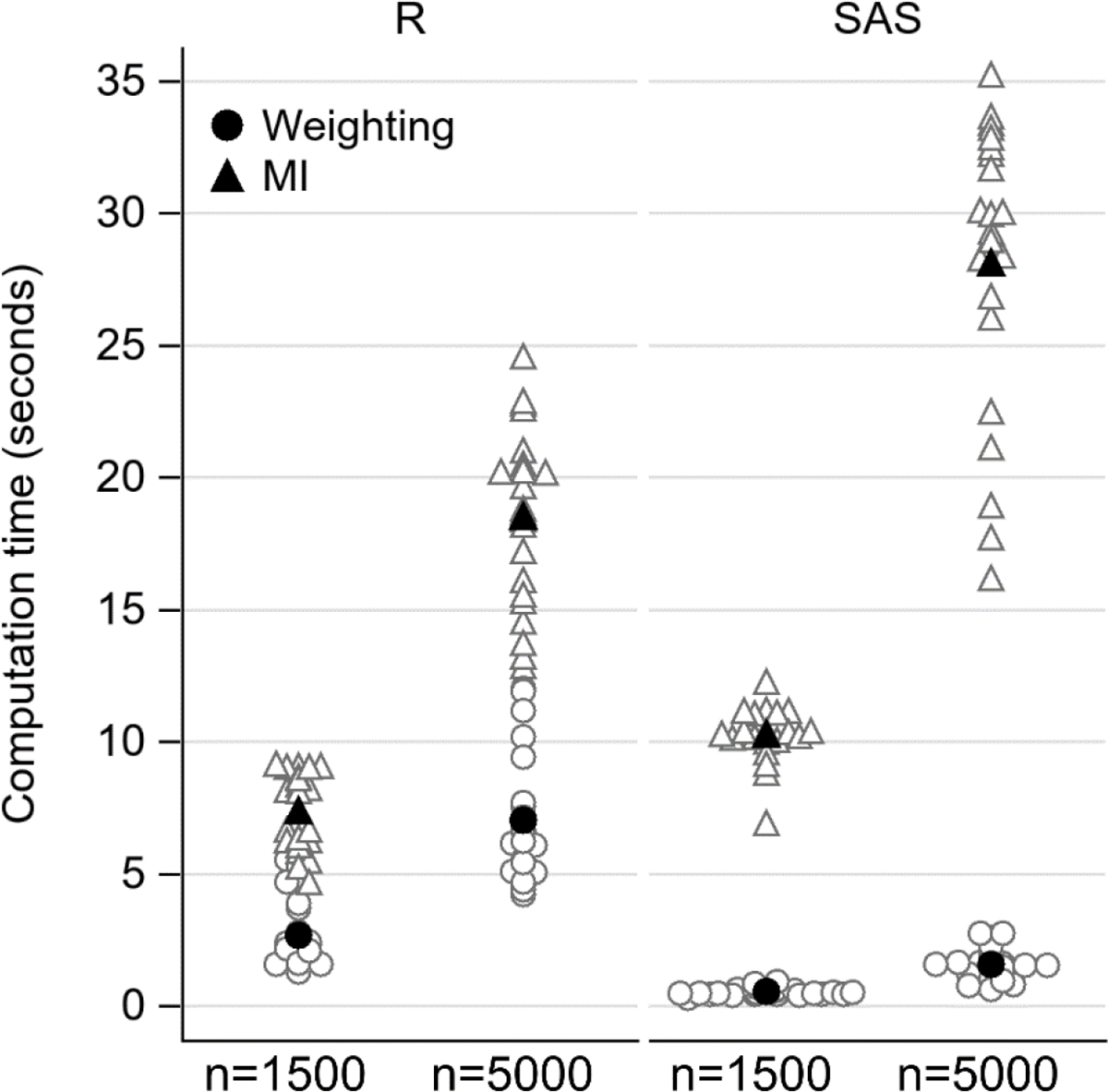
Computational time in seconds to implement MI (triangle) and weighting using UMLE (circle) from 22 scenarios by sample size and computer program. Filled in black symbol marks the mean. Abbreviations: MI, multiple imputation; UMLE, unconstrained maximum likelihood estimator

6. Application

Methods

As outlined above, we aimed to estimate the effect of maternal anemia in pregnancy on the risk of spontaneous preterm birth. We implemented three approaches to address missing data that mirror the simulation study. In all, we used treatments weights to address confounding by gestational age at enrollment, maternal age, maternal HIV serostatus, and birth history including parity, prior preterm birth, and prior stillbirth. We fit a weighted linear-binomial model to estimate the risk difference and obtained Wald-type 95% CIs using the robust standard error. Gestational age and maternal age were modeled with restricted quadratic splines with 4 knots at the 5^th, 35^th, 65^th, and 95^th percentiles.⁴⁹

First, we conducted a complete case analysis restricted to the 781 people with complete data. Second, we implemented weighting for missingness. There were a number of missing data patterns with few people so we combined rare patterns as suggested by Sun and Tchetgen Tchetgen.¹⁶ We combined patterns in two ways: 1) patterns 8 through 16 (each <1%, total 2.4%) resulting in 8 total patterns and 2) patterns 6 through 16 (each <2%, total 5.7%) resulting in 6 total patterns. All observed variables were included in the missingness models. For the combined pattern, the model included variables observed across all patterns in the set: gestational age, nulliparity, and prior preterm birth. We implemented UMLE and CBE (with diffuse priors $\gamma ~N(\mathrm{0,100})$ and $c={10}^{-8}$). We used Gelman-Rubin statistic (Rhat) to assess convergence.⁵⁰ We estimated $\widehat{\gamma }$ by the median across 3 chains of 120,000 iterations with the first half of samples discarded. Using $\widehat{\gamma }$, we estimated the missingness weights for the complete cases and then fit the missingness-weighted treatment propensity score model to estimate the treatment weights. The final weight was the product of the two weights.

Third, we implemented MI by chained equations. We implemented MI four ways varying 1) whether spline terms were created before imputation (active imputation) or after imputation (passive imputation) and 2) imputation model flexibility. The imputation models included all variables from the analysis and the exposure-outcome interaction. To increase flexibility, we included interactions between the outcome and strong outcome predictors: prior preterm birth, maternal age, and HIV serostatus. We imputed missing data 20 times. In each imputed dataset, we fit the treatment propensity score model, estimated the treatment weights and then estimated the risk difference and robust variance from the treatment-weighted linear-binomial model. The 20 estimates were combined by Rubin’s rule (as detailed above).

Results

In the complete case analysis, the estimate of the effect of anemia on spontaneous preterm birth was 2.7 percentage points (95% CI −5.7, 11.0) (Table 7). Although anemia appeared to elevate the risk of preterm birth, the confidence interval was wide and encompassed effects ranging from strongly protective to strongly causative. While addressing missingness resulted in small changes in the point estimate, the confidence intervals remained wide so that these changes were not meaningful. Across the weighting approaches, the point estimates varied from 2.1 to 2.3. There was modest improvement in statistical efficiency with weighting compared to complete case analysis (standard error: complete case 4.3, UMLE 4.0, CBE 4.1). Across the MI specifications, the point estimates varied more widely, from 1.9 to 3.0. The standard errors ranged from 3.8 to 4.1.

Table 7.

Risk difference estimates (in percentage points) and uncertainty from application examining effect of anemia on spontaneous preterm birth

Missing data approacha	RD	95% CIb	SEb
Complete case analysis	2.7	−5.7, 11.0	4.3
Weighting, UMLE, 6 patternsc	2.1	−5.8, 10.0	4.0
Weighting, UMLE, 8 patternsd	2.0	−5.9, 9.9	4.0
Weighting, CBE, 6 patternsc	2.3	−5.8, 10.3	4.1
Weighting, CBE, 8 patternsd	2.2	−5.8, 10.2	4.1
MI, transform/imputee	1.9	−5.7, 9.6	3.8
MI, transform/impute, more flexiblee,f	3.0	−5.3, 11.2	4.1
MI, impute/transformg	2.4	−5.6, 10.5	4.0
MI, impute/transform, more flexibleg,f	3.0	−5.0, 11.0	4.0

Abbreviations: RD, risk difference in percentage points; CI, confidence interval; SE, standard error; UMLE, unconstrainted maximum likelihood estimator; CBE, constrained Bayesian estimator; MI, multiple imputation

^aAll approaches addressed confounding using inverse probability of treatment weights

^bRobust standard error estimated by “robust” (Huber-White) sandwich estimator

^cCombined patterns 6 through 16 (each <2%) resulting in 6 total patterns

^dCombined patterns 8 through 16 (each <1%) resulting in 8 total patterns

^eSpline terms were created first and then missing data were imputed

^fMore flexible imputation models included interactions between outcome and strong predictors of the outcome: prior preterm birth, maternal age, and HIV serostatus

^gMissing data were imputed first and then spline terms were created

7. Discussion

In this work, we illustrated implementation of a novel weighting approach for nonmonotone missing data using data from a cohort (including code) and examined the approach’s comparative performance to the most used approach, multiple imputation. This work provides an important demonstration of the utility of this novel approach and provides tools for its uptake. Our work supports the finding of Sun and Tchetgen Tchetgen that weighting is an alternative to MI to account for nonmonotone missingness. The UMLE estimator for missingness weights is easy to implement in commonly used software and intuitive, in contrast to prior approaches for weighting for nonmonotone missingness.^14–17 We provide code in R and SAS to support uptake of this approach.

Although theoretically UMLE may fail to converge if there are complete cases with a small probability of being a complete case, this was extremely rare in our simulation study (twice in 220,000 simulated cohorts). CBE is an alternative that can be used in these settings, though implementation is more challenging. Future work could examine characteristics of the datasets in which UMLE failed in an effort to anticipate failures. Even when UMLE converges, the weighted outcome model may fail, though, this was also rare in our simulation study (≤0.5% under MAR). Weighting failed when the complete case analysis also failed as both approaches fit the outcome model restricted to the complete cases. The complete case analysis could be used to assess whether weighting is likely to succeed. In our context, failure could also occur, for weighting or imputation, if the treatment propensity score model fails to converge or cannot be estimated due to change non-positivity. Imputation may fail if the imputation models do not converge. Alternative approaches such as robust logistic regression or penalization could be used to address non-convergence of the propensity score or imputation models.⁵¹ UMLE non-convergence was previously examined in a simple simulation by Sun and Tchetgen Tchetgen in which the parameters of interest were the parameters of a logistic model and only missingness weights were used.¹⁶ They reported that UMLE failed in approximately 1% of simulation replicates. However, the authors did not say specifically whether these failures were due to UMLE non-convergence or non-convergence of the weighted outcome model. They also do not report failures of the other approaches.

Generally weighting is a semi-parametric approach; in contrast, the more widely-used MI is a fully parametric approach. The stronger parametric assumption improves precision of MI,¹² however, in our simulation, this improved efficiency was only notable at the smaller sample size with 15% exposure prevalence. This observed relationship with exposure prevalence may be because there was a lot of missingness in the exposure in our simulation (30% in primary scenario marginally). In the other scenarios, there was little practical difference in efficiency between weighting and MI. Increasing the number of imputations may improve efficiency of MI.⁵² To improve efficiency of weighting, augmented weighted estimators (also derived by Sun and Tchetgen Tchetgen) could be used.¹⁶ We chose to use the non-augmented estimators in this work because they are easier to implement and thus more likely to be used in practice.

There were two instances where performance was notably different between weighting and MI. First, when data were MNAR, both MI and weighting were biased, however MI was less biased than weighting. It is not clear whether this is a characteristic of the estimators themselves or a product of our data generating mechanism. In Sun and Tchetgen Tchetgen’s simulation, which examined different parameters of interest than examined in our simulation, there was not a consistent pattern of bias in the estimators across the parameters of interest under MNAR.¹⁶ Second, weighting was computationally faster than MI. At the small sample sizes examined here, the difference was trivial, however with large sample sizes or when estimating the variance using resampling algorithms with a moderate sample size, the difference could be meaningful. Under linear extrapolation of our results, 1000 bootstrap resamples for n=5000 is expected to take 7.8 hours using MI and 0.4 hours using weighting in SAS. In R, MI is expected to take 5.1 hours and weighting 1.9 hours.

In our empirical example, there was little change in the estimates across the approaches and results were imprecise. The application highlights that implementing weighting and MI each require a number of analytic decisions. For weighting, some missing data patterns were rare, so we combined rare patterns. The model for this combined set could only include variables that were observed across all patterns in the set and therefore induced an assumption stronger than MAR. Combining patterns may induce bias, but such bias is likely small given that the combined patterns include few observations.¹⁶ After estimation, it is good practice to examine the distribution of the weights as extreme weights can inflate the variance. Truncation of extreme weights can improve precision though potentially at the cost of bias.⁵³ Arguably, MI demands a greater number of analytic decisions.^12,54 Some of these decisions include: the iterative procedure (Markov chain Monte Carlo vs. chained equations); transforming skewed variables; passive vs. active imputation; number of iterations and imputed datasets; and specifying prior distributions.^{11,54,63,64,55–62}

Both weighting and MI require correct model specification. In MI by chained equations, we specify a model for each variable with missingness. In weighting, we specify a model for each pattern. The number of potential patterns grows exponentially with the number of variables with missingness so weighting will often require specification of more models than MI. The missingness models in weighting all have binomial dependent variables whereas the distribution of the dependent variables in the imputation models may take different distributions. Some imputation approaches assume a normal distribution and if this assumption is grossly violated, performance can be poor.⁶⁰ It may be necessary to transform variables before imputation. Alternatively, to reduce the strength of the correct model specification assumption, nonparametric approaches for imputation, e.g., predictive mean matching,⁵⁷ can be used. Although it has been argued that it is easier to correctly specify the missingness models than the imputation models,¹² accurate specification of models depends on context-specific knowledge of what variables cause missingness and the functional form of those variables with missingness itself (for missingness models) or with the unobserved data (for imputation models). Previous work suggests that imputation may still perform well when imputation models are misspecified.⁶⁵ Future work is needed to investigate performance of weighting under model misspecification. For both MI and weighting, we can include auxiliary variables to increase plausibility of the MAR assumption and potentially improve precision.^12,66 If the auxiliary variables also have missingness, then the complexity of the imputation model will increase and the number of missingness patterns/models for weighting will likely increase. Finally, an important limitation of MI is that specification of the imputation models can impose constraints on the model of interest (i.e., the analyst must ensure the imputation models are congenial with the analysis model).⁵⁷ Issues of congeniality can arise by omitting the outcome or important interactions from imputation models, or using different functional forms of variables in imputation models and analysis models. Departures from congeniality can be avoided by specifying highly flexible imputation models or modifying the standard chained equations approach.^67,68 Congeniality is not a concern with weighting where specification of the missingness models is independent of the full data and therefore does not impose restrictions on the analysis model.

Our work has limitations. Our simulation design was relatively simple compared to most data settings and we did not vary all elements of the data generating mechanism. We mimicked the patterns observed in the application where missing exposure and outcome accounted for most of the missingness and results may differ as these patterns change. Other than the MCAR and MNAR scenarios, we did not vary the strength of relationships between observed data and missingness. We generated missingness in such a way that allowed us to control whether data were MAR. It is arguably more realistic to generate missingness by variable (as opposed to pattern) however such missingness would be MNAR. Future work should examine the performance of weighting under alternative generation mechanisms. Finally, we specifically focused on estimation of marginal causal effects where confounding is addressed via inverse probability of treatment weighting. Comparative performance of weighting and MI may differ for other estimators (e.g., g-computation). A strength of our work is that our simulation employed increased complexity over the only other simulation comparing Sun and Tchetgen Tchetgen’s estimators with MI for nonmonotone missingness.¹⁶ Additionally, in contrast to that previous simulation, we focused on estimating causal effects. We also provide code for the estimators in two commonly used software programs.

Conclusion

Weighting can be used to address confounding and missing data simultaneously.³¹ When missingness is nonmonotone, Sun and Tchetgen Tchetgen’s UMLE is an easy to implement estimator for the missingness weights. Though less statistically efficient, weighting is an alternative to MI. Weighting’s superior computational efficiency may be preferred with large sample sizes or when using resampling algorithms to estimate variance. As validity of weighting and MI rely on correct specification of different models, both approaches could be implemented to check agreement of results.

Data availability statement:

The data that support the findings of this study are openly available in osf at https://osf.io/vzqdf/. Code is available on Github at https://github.com/rachael-k-ross/Wgt-NonmonotoneMiss.