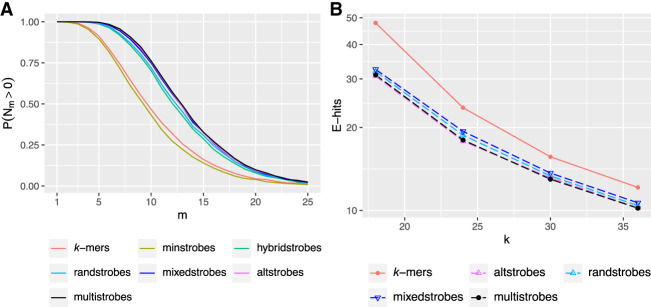
Figure 3.
Simulations showing how pseudorandomness in seed construct influences probability of w consecutive seeds producing at least one match in a region of length 2w = 128 between sequences. Panel A shows P(Nm(30, 64) > 0) for seed constructs k-mers (k = 30), minstrobes, hybridstrobes, and randstrobes with (2,15,25,50), mixedstrobes (2,15,25,50,0.8), altstrobes (2,10, 20,25,50), and multistrobes (2,5,25,25,50). Each P(Nm(30, 64) > 0) estimate is derived from 10,000 instances of pairs of strings S and T. In general, a large gap is observed between non-random constructs (k-mers, minstrobes) to constructs with pseudorandomness (hybridstrobes, randstrobes, mixedstrobes, altstrobes) for most mutation frequencies. The total sum of probabilities across m is higher for constructs with more random appearance. Panel B shows the seed uniqueness as expected number of hits (E-hits) from a seed randomly drawn from human Chromosome 21. Chromosome 21 of the human GRCh38 assembly was seeded with k-mers, randstrobes (2, k/2, 25, 50), mixedstrobes (2, k/2, 25, 50, 0.8), altstrobes (2, k/3, 2k/3, 25, 50), and multistrobes (2, 5, k − 5, 25, 50), whereby the number of extracted nucleotides (k = 30) was the same for all seeding techniques.