Beyond analytic solution: Analysis of FRAP experiments by spatial simulation of the forward problem

Abstract

Fluorescence redistribution after photobleaching is a commonly used method to understand the dynamic behavior of molecules within cells. Analytic solutions have been developed for specific, well-defined models of dynamic behavior in idealized geometries, but these solutions are inaccurate in complex geometries or when complex binding and diffusion behaviors exist. We demonstrate the use of numerical reaction-diffusion simulations using the Virtual Cell software platform to model fluorescence redistribution after photobleaching experiments. Multiple simulations employing parameter scans and varying bleaching locations and sizes can help to bracket diffusion coefficients and kinetic rate constants in complex image-based geometries. This approach is applied to problems in membrane surface diffusion as well as diffusion and binding in cytosolic volumes in complex cell geometries. In addition, we model diffusion and binding within phase-separated biomolecular condensates (liquid droplets). These are modeled as spherical low-affinity binding domains that also define a high viscosity medium for exchange of the free fluorescently labeled ligand with the external cytosol.

Significance

Fluorescence redistribution after photobleaching (FRAP) is a widely used experimental method that can reveal important parameters for reaction/diffusion events within cells. However, analytic methods to analyze FRAP experiments are limited to specific geometries and conditions. We develop a series of template mathematical models using the biologist-friendly Virtual Cell software that can be used to directly compare FRAP experiments to simulation predictions in situations that are not amenable to analytic solutions.

Introduction

Fluorescence redistribution after photobleaching (FRAP) was pioneered by Ken Jacobson and several other renowned biophysicists in a series of seminal papers in 1976 (1,2,3,4). It involves the bleaching of a fluorescent label with a brief but intense illumination in a small region of a cell; the recovery of the fluorescence is then monitored to assess the kinetics of diffusion and/or binding of the labeled molecule. With the advent of laser scanning confocal microscopes, FRAP is now routine in many laboratories, and the development of new labeling methods allows fluorescence probing of increasingly diverse events within cells. Extracting accurate biophysical parameters from such data, however, remains a daunting task. The complex interplay of reaction-diffusion events with each cell’s specific geometry, as well as distortions introduced by imaging systems, preclude the use of available image analysis methods; simple analytic approaches to determine parameter values such as on and off rates, diffusion coefficients, or velocities require assumptions that are rarely met in real experimental situations. Few software tools are available that can aid microscopists in obtaining these parameters. In part, this is because the characteristic time of the response in a reaction-diffusion system is highly dependent on the geometry of both the cell and the experimental perturbation. In addition, distortions introduced by the imaging system are not easily accounted for. However, analytic methods have been successfully developed to analyze specific experimental designs ((5,6,7,8,9,10,11,12,13,14); reviewed in (15)). Most of these methods are mathematically complex, cannot be generalized, and are difficult for cell biologists to apply. These analytic methods necessarily each apply only to a specific class of idealized cell geometries (e.g., sphere, disk, or cylinder) and contain simplifying assumptions that can significantly reduce the accuracy of the kinetic constants determined. More importantly, analytic solutions such as these use only a small subset of the information in the image, e.g., the bleached area of a FRAP experiment, but there is useful information within the entire spatiotemporal data set that can be used to refine the accuracy of the parameters or obtain additional information about the system.

Approaches for analyzing photobleaching and photoactivation experiments based on numerical solutions of reaction-diffusion in two-dimensional (2D) have been published (5,9,16,17), and in several cases have been integrated into software tools. One of the first such software offerings was Tropical (18), which used a sequential optimization method for 2D reaction-diffusion problems. PyFRAP (19) is a Python-based tool for combined image processing and analysis of FRAP in arbitrary 3D geometries, which can estimate diffusion coefficients (or effective diffusion coefficients in cases where binding kinetics are limiting). A tool called simFRAP is provided as an ImageJ plugin, but is restricted to analysis of 2D diffusion (20). A stochastic software tool, DCMS (21), has also been developed for 3D simulations and was applied to analyze diffusion based on FRAP experiments in bacterial cells.

The Virtual Cell (VCell) modeling environment is uniquely suited to simulate dynamic fluorescence imaging experiments because it can solve reaction-diffusion equations within any given geometry (22,23,24). Designed as a general modeling tool specifically for use by experimental biologists, VCell is capable of simulating any reaction-diffusion-advection system defined within the volumes and on the surfaces of arbitrarily shaped 2D or 3D geometries, including geometries obtained from experimental cellular microscopy images. VCell is used by hundreds of researchers around the world, to whom it provides a powerful tool for collaborative research and modeling in computational cell biology.

Many VCell models have been created specifically to simulate experimental fluorescence-based imaging experiments to derive the quantitative biological details of the system being studied. These include models of uncaging reactions (25,26), photobleaching (27,28,29,30), calcium indicator probes (25), translocation of a fluorescent binding protein (31), and fluorescent biosensors (32,33). VCell models are stored within a centralized database, and many of these models have been made available to the public from within VCell.

Here, we show that VCell can be used much more generally to simulate experiments using photobleaching. To validate the utility of using VCell to simulate FRAP experiments, we first applied analytical methods to VCell simulations using idealized geometries and diffusion conditions. We then created a series of VCell models that demonstrate simulation of photobleaching experiments for cytoplasmic or membrane species using various nonideal, experimentally relevant bleaching geometries and cellular geometries. These models can incorporate binding kinetics and we employed a range of rate constants and diffusion coefficients to bracket commonly observed experimental values. We also applied this approach to selected protocols that can dissect diffusion within and binding to biomolecular condensates, which we modeled as a viscous spherical domain within a cell that weakly binds a fluorescently labeled species. Previous methods (34,35) to derive diffusion coefficients within the droplet by model fitting often assume that the available fluorescent label diffuses from an effectively infinite pool (as opposed to from within the limited confines and complex geometry of a cell). They also often model only diffusion and partitioning, assuming fast binding to binding sites within the condensate. Of course, our “forward modeling” approach has no such limitation. In general, our work demonstrates that VCell can be used to solve the forward problem in any realistic 3D geometry, including reaction kinetics and with any bleaching protocol. Thus, we have created a set of public VCell models that can serve as templates for the analysis of complex photobleaching experiments.

Methods

All numerical simulations were performed using the VCell software freely available at http://vcell.org. To view models, simulation specifications, and all simulation results within VCell, download and install the client software and create user credentials to access the central database. Several BioModels were created for simulations, all available to the public from the VCell database under username “les” with the following BioModel names:

FRAP_Membrane_Rel,

FRAP_cyt,

FRAP Condensate Droplet,

FRAP_Cyt_Membrane_Binding.

Planar and spherical geometries for spatial simulations were specified analytically; the 3D experimental cellular geometry was reused from a publicly available VCell Tutorial model and was originally created from a confocal image stack of a differentiated N1E neuroblastoma cell. All BioModels include multiple simulated experiments, called Applications; multiple simulations representing different parameter choices are collected within each Application, as described in the results. The BioModel “FRAP_Membrane_Rel” includes species and bleaching reactions placed in a membrane compartment “PM.” The BioModel “FRAP_cyt” and the BioModel “FRAP Condensate Droplet” places species and bleaching and binding reactions within a volume compartment “CYT” (see Fig. 1); while the reaction diagram for both these BioModels are identical, we elected to use separate BioModels for clarity in defining parameters and initial conditions. In all situations where binding interactions are included, initial (i.e., prebleach) steady-state conditions were established based on the K_D and used as initial concentrations for binding species. Nominal parameter values and species initial conditions are shown in Table 1 with descriptions of what each represents; changes made to the default parameter values are specified in the text and figure legends. A fourth BioModel, “FRAP_Cyt_Membrane_Binding,” includes simulations where a cytosol (CYT) fluorescent molecule binds to a molecule in the plasma membrane (PM), a common occurrence in signaling pathways and is described in supporting materials.

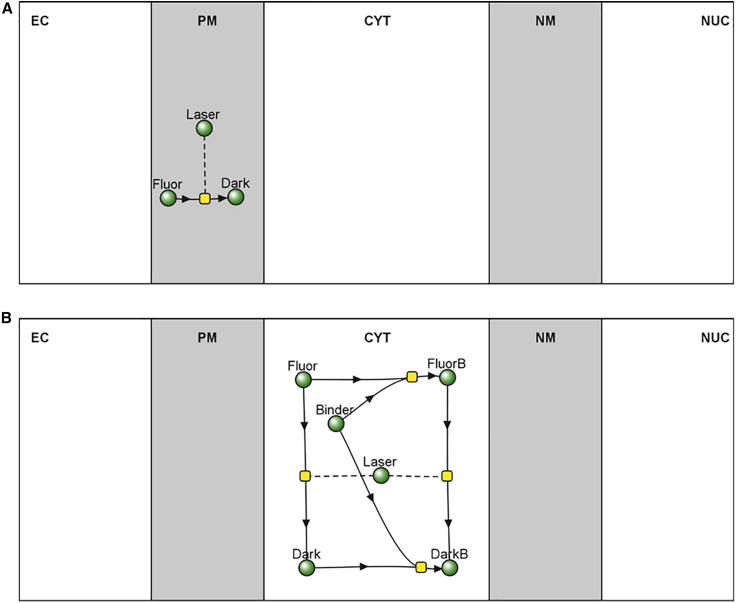
Figure 1.

Reaction diagram for VCell models. (A) FRAP_Membrane_Rel. (B) Frap_Cyt. Gray regions represent 2D surfaces (i.e., membranes) and white regions represent volumes. The green spheres represent species (i.e., variables), the yellow squares represent reactions. An arrow emanating from a species indicates that the species is consumed when the reaction rate is positive, an arrow pointing to a species indicates that species is produced when the reaction rate is positive. Dashed lines indicate the corresponding species (“Laser”) modulates the reaction rate but is neither produced nor consumed. To see this figure in color, go online.

Table 1.

Nominal parameter values and initial conditions in VCell BioModels^a

Parameter	Value	Units	Description
Biomodel FRAP_Membrane_Rel
BleachRadius	2	μm	radius of circular bleaching illumination
Duration	1	s	duration of bleaching flash
Kbleach	10	μm2 s−1 molecules−1	bleaching rate (related to laser intensity)
Kr_Bleach	0	s−1	reverse of the bleach reaction (always set to 0)
sigmaaxial	1.5	μm	axial Gaussian decay length
sigmalateral	0.5	μm	radial Gaussian decay length
Start	1	S	time before start of bleaching flash
Dark	0	molecules μm−2	surface density of bleached Fluor
Dark diffusion coefficient	0.1	μm2 s−1
Fluor	10	molecules μm−2	surface density of Fluor
Fluor diffusion coefficient	0.1	μm2 s−1
Laserb			distribution of bleaching light
Biomodel FRAP_cyt
BleachRadius	2	μm	radius of circular bleaching illumination
Duration	1	s	duration of bleaching flash
Kbleach	1	s−1μM−1	bleaching rate (related to laser intensity)
Kf_BindF	1	s−1μM−1	forward rate for binding of Fluor to Binder
Kf_BindD	1	s−1μM−1	forward rate for binding of Dark to Binder (always = Kf_BindF)
Kr_BindF	1	s−1	FluorB dissociation rate
Kr_BindD	1	s−1	DarkB dissociation rate (=Kr_BindF)
sigmaaxial	1.5	μm	axial Gaussian decay length
sigmalateral	0.5	μm	radial Gaussian decay length
Start	1	s	time before start of bleaching flash
Binder	2.702	μM	initial concentration of Binderc
Binder diffusion coefficient	0	μm−2 s−1
Dark	0	μM	initial concentration of free bleached fluor
Dark diffusion coefficient	10	μm−2 s−1
DarkB	0	μM	initial concentration of bound bleached Fluor
DarkB diffusion coefficient	0	μm−2 s−1
Laserb
Fluor	2.702	μM	initial concentration of free Fluorc
Flour diffusion coefficient	10	μm−2 s−1
FluorB	7.298	μM	initial concentration of FluorB (bound form)c
FlourB diffusion coefficient	0	μm−2 s−1
BioModel FRAP Condensate Droplet
BleachRadius	2	μm	radius of circular bleaching illumination
Duration	1	s	duration of bleaching flash
Kbleach	1	s−1μM−1	bleaching rate (related to laser intensity)
Kf_BindF	0.025	s−1μM−1	forward rate for binding of Fluor to Binder
Kf_BindD	0.025	s−1μM−1	forward rate for binding of Dark to Binder (always = Kf_BindF)
Kr_BindF	2.5	s−1	FluorB dissociation rate
Kr_BindD	2.5	s−1	DarkB dissociation rate (=Kr_BindF)
sigmaaxial	1.5	μm	axial Gaussian decay length
sigmalateral	0.5	μm	radial Gaussian decay length
Start	1	s	time before start of bleaching flash
Binder	591.4	μM	initial concentration of Binderc,d
Binder diffusion coefficient	0.1	μm−2 s−1	diffusion is set to 0 outside the confines of the droplet
Dark	0	μM	initial concentration of free bleached fluor
Dark diffusion coefficient	10	μm−2 s−1	diffusion is set to 10 outside the confines of the droplet and to 1 μm2 s−1 inside
DarkB	0	μM	concentration of bound bleached Fluord
DarkB diffusion coefficient	0.1	μm−2 s−1	diffusion is set to 0 outside the confines of the droplet
Laserb
Fluor	1.446	μM	concentration of free Fluorc
Flour diffusion coefficient	10	μm−2 s−1	diffusion is set to 10 outside the confines of the droplet and to 1 μm2 s−1 inside
FluorB	8.554	μM	concentration of FluorB (bound form)c,d
FlourB diffusion coefficient	0.1	μm−2 s−1	diffusion is set to 0 outside the confines of the droplet
Biomodel FRAP_Cyt_Membrane_Binding
BleachRadius	4	μm	radius of circular bleaching illumination
duration	1	s	duration of bleaching flash
Kbleach	1	s−1μM−1	bleaching rate (related to laser intensity)
Kf_BindF	1	s−1μM−1	forward rate for binding of Fluor to Binder
Kf_BindD	1	s−1μM−1	forward rate for binding of Dark to Binder (always = Kf_BindF)
Kr_BindF	0.1	s−1	FluorB dissociation rate
Kr_BindD	0.1	s−1	DarkB dissociation rate (=Kr_BindF)
sigmaaxial	1.5	μm	axial Gaussian decay length
sigmalateral	0.5	μm	radial Gaussian decay length
Start	1	s	time before start of bleaching flash
Binder	2.111	molecules μm−2	initial surface density of Binderc
Binder diffusion coefficient	0.1	μm−2 s−1
Dark	0	μM	initial concentration of free bleached fluor
Dark diffusion coefficient	25	μm−2 s−1
DarkB	0	μM	initial surface density of bound bleached Fluor
DarkB diffusion coefficient	0.1	μm−2 s−1
Laserb
Fluor	0.473	μM	initial concentration of free Fluorc
Flour diffusion coefficient	25	μm−2 s−1
FluorB	997.9	molecules μm−2	initial surface density of FluorB (bound form)c
FlourB diffusion coefficient	0.1	μm−2 s−1

^aThese default parameters in each BioModel are varied in the simulations to model different experimental scenarios. The actual parameter values used in the figures in this work are described in the text and figure captions.

^bThe Laser variable defines the pattern of illumination in space and is presented in each Application as a function: Laser = f(x, y, z).

^cThe prebleach concentrations are set to the steady-state values for the default K_D.

^dIn BioModel “FRAP Condensate Droplet” and the species Binder, FluorB, and DarkB are all confined to a spherical droplet by setting their initial concentrations and diffusion coefficients to be 0 outside the sphere. Shown here are their nominal diffusion coefficients and initial (prebleach) concentrations within the sphere. The K_D and initial concentrations are set to correspond to a partition coefficient of 7, corresponding to the ratio of TotalF (free plus bound fluor) within the droplet to Fluor outside the droplet.

The default Fully-Implicit (adaptive time step) Finite Volume, Regular Grid solver was used for all spatial simulations, using default Error Tolerance values. For “FRAP_cytosol” and “FRAP Condensate Droplet” simulations, which use VCell “Microscope Measurement Protocols”, the Z projection function was selected in order to sum FluorB and Fluor into a single “fluorescence” value to produce the equivalent of a maximum value projection over the z-slices. Fluorescence curves analyzing binding to a uniformly distributed immobile binding component in the CYT were generated in ImageJ by exporting the Z-projection “fluorescence” data from VCell as a .nrrd file; these data were then analyzed in ImageJ to collect average intensity within either the entire 4 μm diameter bleach region or, for the models when half the cell was bleached, in a 4 μm circle centered within the bleach region. Data were normalized as (I_t – I₀)/((I_i – I₀) fb) where I_t is intensity at time t, I₀ is the intensity immediately postbleach, I_i is the prebleach intensity and fb is the fraction of total intensity remaining after the bleach. In the Biomodel “FRAP Condensate Droplet,” FRAP curves were analyzed in VCell either by integrating the function TotalF (= Fluor + FluorB) over the 3D spherical droplet at each time point or with kymographs along the diameter of the droplet. Additional details of each simulation can be obtained either directly from the publicly available VCell models or from the VCell-generated BioModel reports in supporting material.

Results

Setting up bleaching and binding reactions in VCell

For consistency, all VCell models used in our analyses describe five cellular compartments: extracellular, PM, cytosol (CYT), nuclear membrane (NM), and nucleus (NUC). (Note that the NUC and NM compartments are only required to simulate cytosolic diffusion, which is excluded from the nuclear region; however, they are included in the membrane bleach simulations so the same experimental geometry could be applied to both types of bleaching experiments.) The basic photobleaching reaction is modeled using three species: a fluorescent molecule (Fluor), the dark form of the molecule after photobleaching (Dark), and a species (Laser) used to describe the bleaching intensity as a function of time and space. To model photobleaching of membrane components, the species are placed in the PM compartment, which is modeled as a surface. To model photobleaching of cytosolic components, the species are placed in the CYT compartment, which is modeled as a volume. A single rate expression describes the bleaching reaction that transforms Fluor into Dark using a rate law of:

$$J_{\left(Bleach\right)}=kbleach·Flour·Laser·\left(t>start\right)·\left(t<start+duration\right)$$ (Equation 1)

Where kbleach is a parameter that defines the strength of the bleaching beam, Fluor is the variable representing the concentration of the fluorescent molecule, and Laser is a variable representing the position of the bleaching beam; as a variable Laser can be defined by any arbitrary function or field and thus mapped to any arbitrary position in x, y, and z in the compartment geometry. Figs. S1 and S2 show different bleach patterns for the CYT compartment. The expression kbleach · Fluor · Laser is constrained to a specific time range by multiplying by the Boolean expressions (t > start) and (t < start + duration); Boolean expressions evaluate to 1 when true and 0 when false and thus restrict the bleaching reaction to the time between the start and end time (=start + duration) of the bleaching reaction. Start and duration are defined as parameters so they can be easily varied within simulations to match a particular experiment. Because photobleaching is, generally, irreversible, the reverse rate constant for the reaction, Kr_Bleach, is always set to 0; note that a reverse reaction could be included to model the case of dark state to light state transitions during the experiment. This simple reaction rate law is all that is needed to model a simple photobleaching experiment with only diffusion.

For models that include binding of the labeled molecule to an unlabeled binding partner, we also include a pair of identical reversible mass action reactions between a species called “Binder” and, respectively, Fluor and Dark; the products of these reactions are respectively, FluorB and DarkB. The rates of these reactions are given by:

$$J_{FlourB}=\left(Kf·Flour·Binder\right)-\left(Kr·FlourB\right)$$ (Equation 2)

and

$$J_{DarkB}=\left(Kf·Dark·Binder\right)-\left(Kr·DarkB\right)\text{.}$$ (Equation 3)

If we are to only consider diffusion, we can either set the forward and reverse rate constants, K_f and K_r, to 0, or we can set the initial concentrations of Binder, FluorB, and DarkB to 0. If we do wish to consider the effect of binding, we set the initial concentrations of the species Fluor, Binder, and FluorB to their steady-state equilibrated values, so that the bleaching event is the only trigger for the subsequent dynamics (Dark and DarkB are, of course, 0 before the bleaching event). Importantly, we also need to include a bleach reaction that converts FluorB to DarkB under the influence of Laser, using the same rate law described above. The diagram in Fig. 1 B shows the relationships of the variables (i.e., species) in this kinetic scheme. When analyzing the simulation results, we often compute the TotalF (=Fluor + FluorB), as this is the experimental observable.

VCell simulations of ideal 2D diffusion are well fit by theory

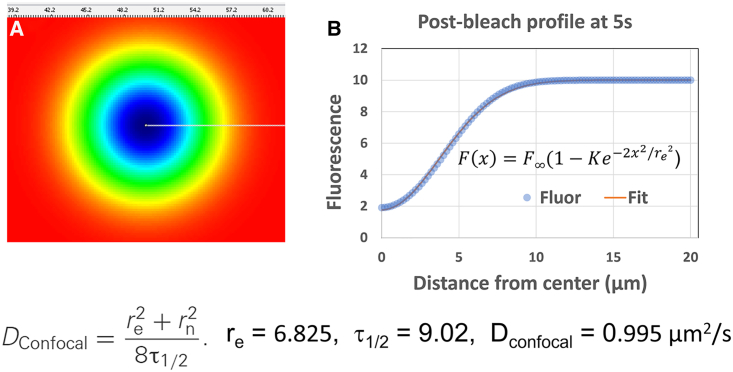
Historically, analytical theories developed for FRAP were idealized to solve for small bleaching spots in an infinitely large 2D surface. The diffusion analysis described in Kang et al. (36) was developed to more accurately analyze photobleaching experiments using a circular bleach on a scanning confocal microscope. This analytic solution uses the radius of the originally prescribed illuminated region and the Gaussian radius of the bleached region at some later time to solve for the diffusion coefficient using the equation:

$$D_{confocal}=\left(r_e^2+r_n^2\right)/{8\tau }_{1/2}\text{,}$$ (Equation 4)

where r_e is the effective radius of the bleached area determined using a Gaussian fit at some time t after bleaching, r_n is the nominal experimentally defined radius of the bleach region, and τ_1/2 is defined as the half time of recovery from time t, measuring the average fluorescence over the entire initial bleach surface area. We examined how well this analytic approach was able to recover the diffusion coefficient defined in our VCell simulations.

As an initial test we created simulations in which the fluorescent molecules were uniformly distributed in a 100 × 100 μm 2D membrane sheet (PM) with value boundary conditions to provide an infinite source of Fluor (BioModel “FRAP_Membrane_Rel,” Application: “100 μm planar membrane, value BC”). This condition closely approximates the assumption of an infinite source of fluorophore that is used to obtain the analytic solution developed by Kang et al. (36). In the simulations the bleached region is defined by placing the immobile Laser species that catalyzes the bleaching reaction within a circle of given radius centered at x = 50, y = 50. Results of simulations with a fixed value boundary condition for Fluor, with a diffusion coefficient set to 1 μm²/s and an initial bleach (r_n) of 4 μm diameter are shown in Fig. 2. We found the earliest postbleach profile that was well fit by a Gaussian profile occurred at 5 s in the simulation (3 s after termination of the Bleach) and yielded a value for r_e of 6.825 μm and τ_1/2 of 9.02 s, resulting in a calculated D of 0.995 μm²/s. Similar analyses with a bleach radius (r_n) of 1 and 3 μm yielded diffusion coefficients of 0.989 and 1.005 μm²/s, respectively. These are all gratifyingly close to the input value of 1 μm²/s. As an additional check, we also used 0 flux boundary conditions and achieved virtually identical results, indicating that the 100 × 100 μm² was sufficiently large that boundary effects were insignificant. We conclude that VCell simulations accurately reproduce diffusive behavior and that the Kang et al. (36) analysis is highly accurate in appropriate experimental settings.

Figure 2.

Simulations of FRAP within a 100 × 100 μm plane, analyzed by the methods of Kang et al. (36). A fluorescent species Fluor with D = 1 μm²/s was placed in the surface with boundary conditions clamped at a value of 10 μM. A 4 μm radius bleach area was defined in the center of the membrane plane (duration 1 s at t = 1 s). (A) Simulation snapshot at t = 5 s (3 s postbleach). (B) Postbleach profile along the line indicated in (A) at t = 5 s fit to a Gaussian to obtain r_e. τ_1/2 was determined by finding the 50% recovery time from the 5 s time point, using the mean fluorescence within the bleached 4 μm radius bleached area. To see this figure in color, go online.

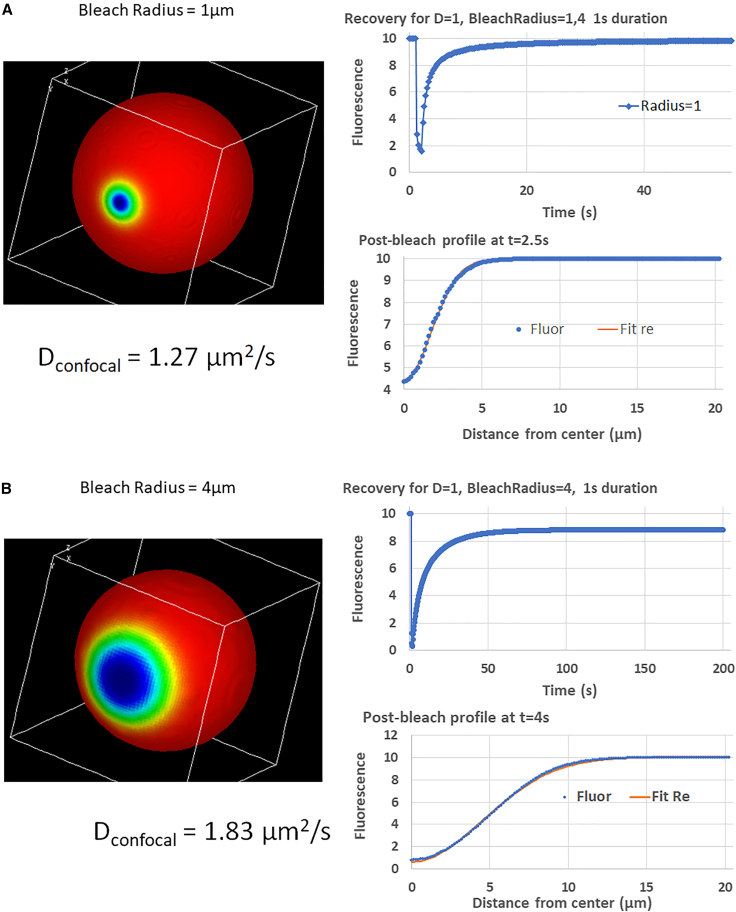
To more closely represent an idealized cell membrane, we then created simulations using a 3D spherical surface of 20 μm diameter using analytic expressions to describe the geometry; it was placed within a cubic simulation domain of 22 μm on each side. Bleach areas were defined using a Boolean expression to restrict the position of the Laser species to a circle of the chosen radius centered at x = 11, y = 11, and a Gaussian distribution in Z depending on the effective numerical aperture of the microscope optics.

$$Laser=e^{-\frac{{(z-1.0)}^2}{2.0\left({sigmaaxial}^2\right)}}\ast \left(\left({(x-11)}^2+{\left(y-11\right)}^2\right)>\left({BleachRadius}^2\right)\right)$$

The parameter sigmaaxial is used to specify the characteristic length of the Gaussian distribution in z, which is centered at the top of the spherical membrane (z = 1); the parameter BleachRadius defines the radius of a circular scan region in x and y. Simulations were then run by varying D, duration, and BleachRadius under conditions where the bleach is highly focused (sigmaaxial = 1.5 μm) or when the bleaching beam can be approximated as a column in z (sigmaaxial = 30 μm). The former might be considered equivalent to a two-photon bleaching profile, while the latter is a more conventional confocal or widefield profile and would bleach both the top and bottom surfaces of the cell. The VCell public model is “FRAP_Membrane_Rel” by user “les”; the Application within this model that simulates the spherical membrane is “Spherical_Cell_Circular_Bleach.” As the radius of the bleach region expands, one would expect that the analytic solution will diverge from the prescribed diffusion coefficient of 1 μm²/s because the condition of an infinite source of fluorescent molecule is violated. As shown in Fig 3, we find that this is indeed the case; whereas with a BleachRadius of 1 μm the calculated diffusion coefficient is 1.27 μm²/s; using a BleachRadius of 4 μm the D_Confocal is calculated to be 1.83 μm²/s. Thus, for the larger bleach area, the assumption that the surface of the sphere can be approximately taken as infinite leads to less accurate estimation of D. This is our first indication that more accurate approximations may be obtained by iteratively matching multiple simulations with varying D to the experimental data, rather than attempting to solve the problem analytically.

Figure 3.

Analysis of FRAP on a spherical membrane surface with 1 μm (A) and 4 μm (B) bleach radius. The prescribed D for the Fluor species was 1 μm²/s. Analysis of the recovery was performed as in Fig. 2, with the Gaussian fit to the postbleach profiles performed at 2.5 s (0.5 s postbleach) and 4 s (2 s postbleach) for (A) and (B), respectively. To see this figure in color, go online.

Numerical simulations of membrane FRAP experiments in cells with complex geometries

As shown above, the ideal analytical solutions of FRAP experiments becomes less accurate in situations where a significant fraction of the fluorescent molecules are bleached. We now provide an example of how the complex geometry of a real cell will further complicate the situation. Fig. 4 shows a simulated photobleaching experiment based on a 3D confocal image of a neuroblastoma cell. VCell includes tools for the import of image stacks and their segmentation to enable their use as geometries for simulations. For this work, the geometry was obtained from the VCell database of public models. Simulated bleaching of a circle in the center of cell, over the nucleus, reveals that dynamics in the bleach region are largely the same whether only one membrane is bleached (i.e., as if using a bleaching beam in TIRF optics) or when both the top and bottom membrane of the cell are bleached (e.g., using a lower NA lens to approximate a bleaching area as a column through the cell). Applying the analysis of Kang et al. (36) produces D values of 1.34 and 1.21 μm²/s for these two experimental approaches compared with the input D of 1 μm²/s. However, bleaching an equivalent area of a thin process leads to vastly slower redistribution curves in the bleach region, because diffusion of fluorescent species from the bulk of the cell is restricted by having to enter the thin region that is small compared with the bleached area (37). In such cases, the time course of redistribution can have profound effects on reaction kinetics within the process as, for example, demonstrated by Brown et al. (38) in their analysis of PIP2 diffusion in dendritic spines. In this situation, using numerical simulation to match the time course for fluorescence redistribution is the most accurate way of both assessing diffusion and determining how different geometries affect reaction kinetics.

Figure 4.

Recovery curves for membrane FRAP in three regions of an image-based geometry of a differentiating N1E neuroblastoma cell. The radius of the Laser bleaching region is 2 μm and the bleach starts at t = 1 s and ends at t = 2 s. D = 1 μm²/s. The top and bottom bleached region were analyzed as in Fig. 2. Simulations corresponding to the Top and Bottom virtual experiment can be found in BioModel “FRAP_Membrane_Rel” within the Application “CircularBleach Center Image based”; for the Process simulation, see the Application “Image-based process circle bleach". See Videos S1 and S2 for the full time course of the top and process bleached region. To see this figure in color, go online.

Using numerical simulation to analyze diffusion and reaction in a volume

As noted by Kang et al. (36), solving the inverse problem to characterize diffusion within the cytosol using analytic approaches presents additional difficulties. Compared with the high viscosity membrane environment, free diffusion is much faster in cytosol, and thus requires very fast collection of images and larger bleaching areas to allow one to capture the appropriate dynamics. To collect images rapidly, photobleaching experiments involving cytosolic components are often collected using widefield optics such that fluorescence from the entire cell is convolved in a single 2D image. However, the widefield results do not conform to a 2D diffusion model, especially in the case of complex cellular geometries. Furthermore, using a larger geometry of the bleach region also increases the error from application of analytical solutions to derive D, and large organelles such as the nucleus can distort the free space available for diffusion. Therefore, accurate numerical solutions of the forward problem can be advantageous. Using the full cellular geometry (e.g., from confocal image stacks) and a 3D representation of the bleaching intensity allows accurate numerical simulation, where parameter scans of the diffusion coefficient can be performed. The simulation data may be flattened or convolved for direct comparison with experimental images or to Z-projections of confocal stacks.

In addition, binding to immobile or slowly moving components further complicates the analysis, as described previously (7,9,12,39). Analytic solutions for assessing binding reactions using fluorescence photobleaching generally utilize different methods depending on the relative contributions of binding kinetics and diffusion time to the fluorescence redistribution (9,12,39). When binding is fast relative to diffusion time, fluorescence redistribution curves are dominated by diffusion—a diffusion-limited regime. At the other extreme, high affinity binding with slow off rates are “reaction-dominant” and yield curves that are well fit to a single exponential expression directly related to the off-rate. The real difficulty lies in cases where binding and diffusion timescales are similar. Again, solving the “forward problem” with parameter scans can be applied.

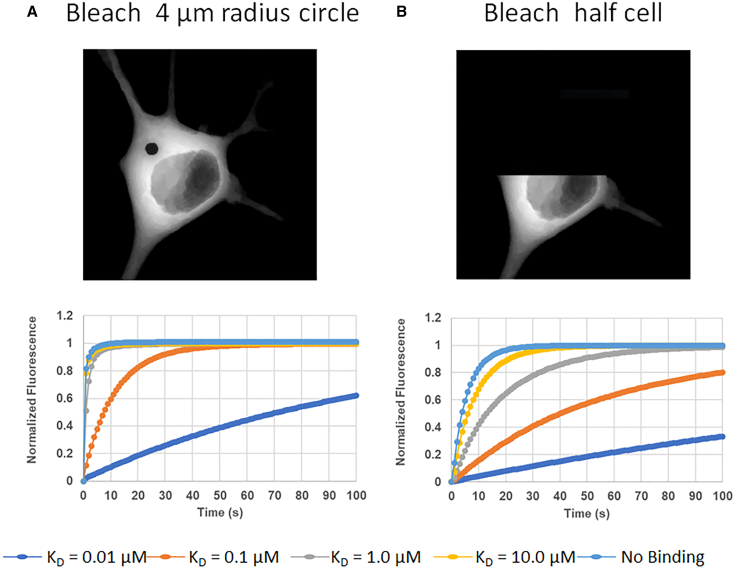
To illustrate the value of numerical simulation methods to analyze different experimental protocols and assess how parameters affect potential results, we created models for photobleaching of cytosolic components using the VCell Biomodel “FRAP_Cyt” by user “les.” These simulations utilized the same 3D cellular geometry used in the plasma membrane applications. The bleach region was specified by restricting the Laser as described for membrane bleaching; using a small “sigmaaxial” value can be used to simulate photobleaching using two-photon excitation, a larger sigmaaxial value to approximate the much longer pattern of one-photon excitation, and a very small sigmaaxial value to approximate bleaching using total internal reflection optics.

We focus here on one-photon excitation, as would be common in a widefield or confocal microscope (additional simulations with “two-photon” or “TIRF” Laser bleaching can be found in the VCell Biomodel “FRAP_Cyt”; Fig. S1 provides examples of the Laser distribution and Fluor distribution at the end of the bleach for these different configurations). The effect of different geometries and bleaching configurations on the dynamics of fluorescence intensity measured in the bleach region was assessed in both the absence and presence of binding reactions where one of the binding components is immobile (additional applications are provided in the BioModel where the binding components are slowly diffusing relative to the free fluorophore). VCell provides the functionality to perform simulations in a 3D geometry, and then flatten all of the fluorescent species into a 2D distribution of “fluorescence” by either summing through z or convolution with a point spread function. Fig. 5 shows such images of simulated fluorescence at the time point immediately postbleach for two different bleaching protocols, either a small circular region 4 μm in diameter (Fig. 5 A, top), or bleaching an entire half of the cell (Fig. 5 B, top). The corresponding time courses for recovery are shown below each of these images. In these simulations, the total concentration of both binding sites, Binder + FluorB, and fluorescent molecules, Fluor +FluorB, are 10 μM, distributed between bound and free forms as determined by the K_D; Fluor was given a diffusion coefficient of 25 μm²/s, while the binding sites (Binder) and complex (FluorB) were immobile. K_r for the binding reaction was varied in 10-fold steps from 0.01 to 10 s⁻¹ and K_f was held constant at 1 μM ⁻¹ s⁻¹; thus, the K_D values are, respectively, varied from 0.01 to 10 μM. Bleaching a 4 μm circle yields much different kinetics when K_r is slow (0.1 or 0.01 s⁻¹), but is indistinguishable from no binding when K_r is fast (1 and 10 s⁻¹) (Fig. 5 A, bottom). However, when half the cell is bleached, the time course for fluorescence redistribution is slower than with no binding even when Kr is fast (Fig. 5 B, bottom). Thus, bleaching a small circular bleach makes it difficult to identify low-affinity binding interactions; bleaching a much larger region (e.g., half the cell) reveals very different time courses even with fast off rates. This effectively illustrates how a simulated experiment can aid in the design of the most informative laboratory experiments. Other scenarios, such as when Binder and complexes are allowed to diffuse slowly, holding the K_D constant while synchronously varying K_f and K_r, or varying D, may be found in BioModel “FRAP_Cyt.” Another commonly encountered situation is that the binding component is in the plasma membrane. The BioModel “FRAP_Cyt_Membrane_Binding” explores different applications of photobleaching in this scenario, and Fig. S3 shows the expected decay of fluorescence intensity near the plasma membrane when Fluor in cytoplasm is continuously bleached (a FLIP experiment) at different binding strengths. It is thus possible to define different scenarios where the influence of binding and diffusion components on redistribution curves can be effectively isolated under the exact conditions of an experiment.

Figure 5.

Simulated photobleaching of cytosolic species with immobile binding partners and varying K_D. (A) Top: simulated fluorescence created from a Z-projection of convolved fluorescent species taken immediately after bleaching a 4 μm diameter region in the CYT. The image is from a simulation where K_D = 1 μM (Kr = 1 s⁻¹). Simulated fluorescence can be created using a convolution function to approximate the experimental distribution of fluorescence molecules predicted from a simulation. Bottom: normalized fluorescence curves from five different simulations where K_D is varied by changing Kr and measured within the entire initially bleached 4 μm diameter region. (B) Top: simulated fluorescence immediately after photobleaching the top half of the cell. Bottom: normalized fluorescence curves from five different simulations where K_D is varied by changing K_r while holding K_f constant. Average fluorescence in the same 4 μm diameter circle as in (A) is plotted. All simulations are in VCell BioModel “FRAP_Cyt.” The Applications corresponding to (A) and (B) are, respectively, “ProjectZ Convolved Image-based center circular bleach vary Kd” and “ProjectZ Convolved Image-based half bleach vary Kd.” Videos S3, S4, S5, S6, and S7 correspond to the five conditions in (A). To see this figure in color, go online.

Diffusion and binding in liquid droplets

Biomolecular condensates, also known as liquid droplets or membraneless organelles, are subcellular aggregates of weakly binding proteins and/or nucleic acids. The biology of liquid droplets has developed explosively because they are so ubiquitous and appear to organize many cellular functions (40,41,42). Their biophysical properties can be understood within the thermodynamic framework of phase separation as well as polymer physics (43,44). Experimentally, FRAP has been a valuable tool to elucidate the dynamics of liquid droplets (34,45,46). Indeed, in a classic paper (47), FRAP was critical to demonstrate that “P granules” are liquid droplets, showing that they localize to one end of a germ-line cell by dissolving and recondensing. However, the complexity of the multiple processes that govern the results of a FRAP experiment (binding, diffusion in the cytosol, diffusion within the droplet) makes interpretation difficult and can even lead to faulty conclusions (34,35). In this section, we exemplify how modeling and simulation of virtual FRAP experiments can help to dissect the key biophysical properties of liquid droplets.

We use the same simple FRAP with binding reaction scheme in the CYT as described in Fig. 1 B and applied in Fig. 5. However, instead of having the Binder evenly distributed within the CYT, we confine it to a spherical droplet of 4 μm diameter situated just outside the nucleus (Fig. 6, top, center; the Z-projection images shown in the figure appears to show the droplet within the nucleus, but it is actually well above the nucleus in the axial direction). The default or baseline model considers the binding to be low affinity (K_D = 100 μM) to a high abundance of binding sites: total = [Binder] + [FluorB] + [DarkB] = 600 μM. Before the bleach, the steady-state concentrations are: [Fluor] = 1.446 μM, [FluorB] = 8.554 μM, and [Binder] = 591.446 μM. The initial total fluorescence (TotalF) is then 10 μM in the droplet (Fluor + FluorB) and 1.446 μM external to the droplet, corresponding to a partition coefficient of 7. Other default parameters in the model give the unbound species, Fluor and Dark, diffusion coefficients of 10 μm²/s outside the droplet, but 1 μm²/s inside the confines of the droplet, corresponding to a 10-fold higher viscosity. The default diffusion coefficients for the Binder, FluorB, and DarkB, are all set equal to 0.1 μm²/s within the droplet (and 0 outside to keep them confined). This lower diffusion coefficient models the droplet as a densely interconnected, but liquid, matrix of macromolecules.

Figure 6.

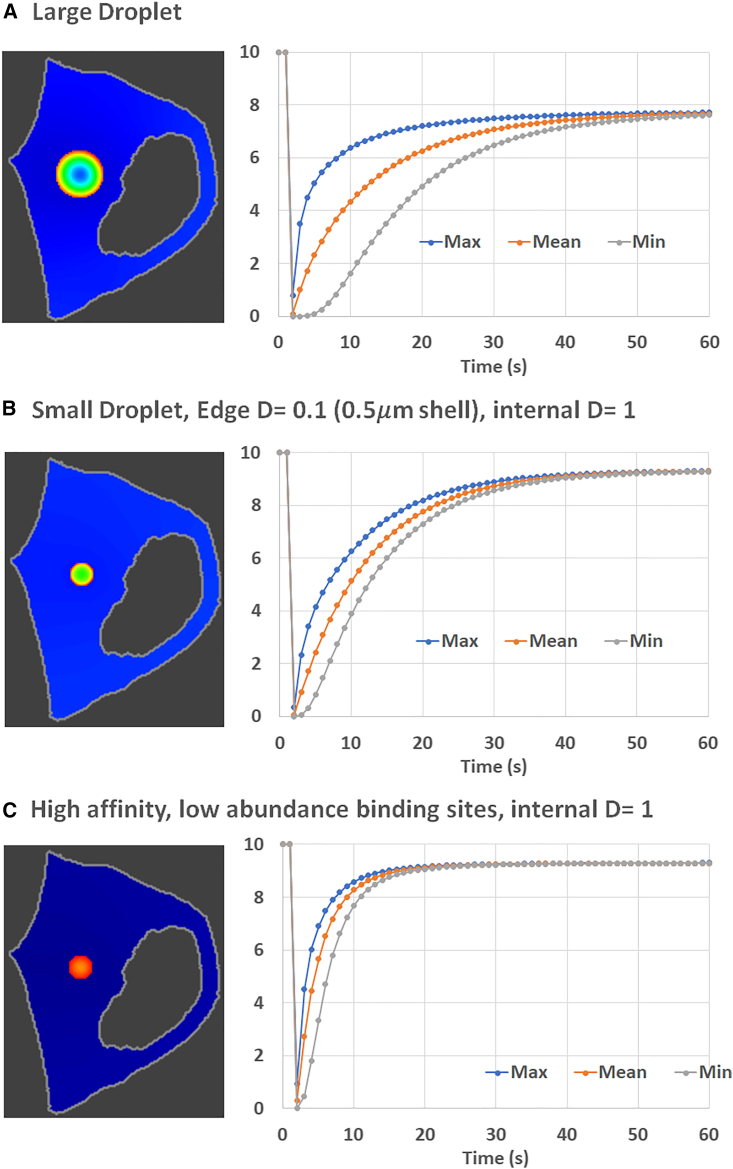
Total bleach of 4 μm diameter spherical liquid droplet with varying diffusion coefficients and off rates. Top left is a 3D surface rendering of the plasma and nuclear membranes. The top center and right images are maximum intensity projections of the total fluorescence in the simulated cell. In (A)–(D), each image shows total fluorescence (TotalF = Fluor + FluorB) in a central slice at 10 s of simulation time (8 s postbleach). Diffusion coefficient of free Fluor and Dark (parameter DropletD) within the droplet and on rate for binding to fixed binding sites within the droplet are indicated above each image. Color scale, 1.14–8.6 μM (blue to red). The corresponding complete recovery curves are shown below each image for the entire spherical droplet. Outside the droplets, Fluor and Dark have D = 10 μm²/s. For all these simulations, the diffusion coefficient of binding sites (parameter BinderD) is 0.1 μm²/s; the K_D is 100 μM with a total concentration of binding sites of 600 μM within the droplets. All simulations can be found in VCell BioModel “FRAP Condensate Droplet” in the Application “Small Liquid Droplet Edge Dif Barrier Image-based.” To see this figure in color, go online.

The simulated experiment in Fig. 6 A uses these default parameters to model a 1 s bleach duration starting at t = 1 s with the Laser positioned to encompass the entire droplet. It also uses an on rate constant, K_f, of 0.025 μM⁻¹ s⁻¹ and an off rate constant, K_r, of 2.5 s⁻¹. The image in Fig. 6 A is a slice through the center of the droplet at the 10 s time point (8 s postbleach). It indicates substantial recovery throughout the volume of the droplet even at this early time. The plots show the full recovery curves analyzed within a 3D region of interest defined to exactly encompass the 3D droplet. The separate plots for the Max, Mean, and Min, report the TotalF, respectively, at the periphery, averaged over the entire droplet, and in the center of the droplet volume. Fig. 6 A thus indicates that, for the default diffusion coefficients of 1 μm²/s for the free and 0.1 μm²/s for the matrix-bound species, diffusion is relatively fast compared with binding.

Fig. 6, B–D explore how slower diffusion and slower binding kinetics affect the virtual FRAP experiment. Fig. 6 B shows how slower diffusion of unbound species within the droplet decreases the rate of recovery and also accentuates gradients within the droplet. This is because the decreased diffusion decreases the rate of penetration of fresh Fluor from the external pool. Fig. 6 C has decreased on and off rate constants (maintaining the same K_d) compared with the baseline parameters in Fig. 6 A, revealing a strong decrease in recovery rate and no diffusive gradient. In this regime of slow kinetics, decreasing diffusion by a factor of 10 has very little effect (Fig. 6 D). Previous analyses of FRAP in liquid droplets were only focused on deriving diffusion coefficients and did not account for the potentially strong influence of unbinding kinetics; they implicitly (45) or explicitly (46) assume that association and dissociation with liquid droplet binding sites is fast on the timescale of diffusion within the droplet. Fig. 6 shows how slow kinetics can change the FRAP recovery patterns, underlining the importance of using parameter scans to bracket the observed experimental results. These simulation results and many additional examples of parameter combinations can be found in the VCell model “FRAP Condensate Droplet” in the Application “Small Liquid Droplet Edge Dif Barrier Image-based.”

Fig. 7 displays three other scenarios for comparison with the baseline model in Fig. 6 A. In Fig. 7 A, we examine the effect of fully bleaching a droplet that is twice the diameter of the one in Fig. 6 A. As would be expected for a diffusion limited regime, the recovery curves are significantly slower and the spatial gradients within the droplet are exaggerated. The simulation for Fig. 7 A can be found in the Application “Large Liquid Droplet Edge Dif Barrier Image-based” along with many other simulations on the 8 μm droplet including with other diffusion coefficients and binding kinetics. Fig. 7 B displays results for a 4 μm droplet with an additional edge diffusion barrier, as has been postulated at the interface of biomolecular condensates (46,48). This was modeled as a 10-fold lower D for the free species diffusion within a 0.5 nm shell on the periphery of the droplet. The rest of the droplet had the same D (1 μm²/s) as in Fig. 6 A. Thus, Fig. 7 B shows that even a thin shell with a high diffusion barrier can significantly slow the recovery. Finally, Fig. 7 C asks whether decreasing the K_D and reducing the binding site abundance can affect the FRAP recovery rate. We increased the affinity by using a K_D of 0.224 μM and decreased the total concentration of binding sites to 10 μM. This allowed us to preserve the same partition coefficient, 7, as in the baseline model. We also preserved the off rate constant of 2.5 s⁻¹ (on rate constant was therefore 10.42 μM⁻¹ s⁻¹). Fig. 7 C reveals that the recovery curves in this high-affinity/low-abundance scenario are identical to the recovery curves in Fig. 6 A. This confirms that, even in this complex model, the key parameters for FRAP dynamics are the off rate and the diffusion coefficient.

Figure 7.

(A) Diffusion becomes limiting in a large 8 μm diameter droplet; D = 1 μm²/s. (B) Diffusion also slows recovery for a 4 μm droplet with an additional peripheral diffusion barrier of 0.1 μm²/s within a 0.5 μm shell. (C) The recovery does not depend on the affinity or abundance of binding sites, for a given K_r. For all three figures, the diffusion within the droplet of unbound species (DropletD) is 1 μm²/s, K_r = 2.5 s⁻¹, and the partition coefficient is 7. K_D = 100 μM for (A) and (B) with total concentration of binding sites in the droplet of 600 μM; for (C) K_D = 0.24 μM and the concentration of binding sites is 10 μM. Color scales, 0.49–6.4 μM in (A and B, blue to red) and 1.14–8.6 μM in (C) (as in Fig. 6). Other parameters are the same as Fig. 6. Simulations can be found in VCell BioModel “FRAP Condensate Droplet”; for (A), see the Application “Large Liquid Droplet Edge Dif Barrier Image-based.” Simulation for (B) can be found in the Application “Small Liquid Droplet Edge Dif Barrier Image-based”; simulation for (C) can be found in the Application “Liquid Droplet Low Kd, low [binder] Edge Dif Barrier Image-based.” Videos S8, S9 and S10 show the time courses for (A–C), respectively. To see this figure in color, go online.

Diffusion of all the constituents within the droplet is a key hallmark of its liquid nature. An established experiment to probe for diffusion within the droplet has been to photobleach half of it (35,46,47). The fastest and most accurate measurement technique is to acquire confocal line scans through the middle of the droplet to build a kymograph. However, as explored in Fig. 8, the recovery is governed by both diffusion from the unbleached half and the kinetics of exchange with the free fluorescent species. Because experiments of this type usually are done on large condensates, we model these experiments using an 8 μm diameter droplet (Fig. 8 A). We compared simulations where the bound species have the default slow diffusion coefficient (parameter BinderD) of 0.1 μm²/s to simulations where BinderD was set to 0. The latter models a gel rather than a liquid droplet (46). In all cases, the unbound species (Dark and Fluor) are given the default diffusion coefficients of 1 μm²/s within the droplet and 10 μm²/s outside the droplet. Fig. 8, B and C compare the liquid to the gel condensate matrix with on and off rate constants set to the baseline values of 0.025 μM⁻¹ s⁻¹ and 2.5 s⁻¹, respectively. While setting BinderD to 0 (Fig. 8 C) does produce a kymograph with overall slower recovery, there is no obvious qualitative difference compared with the kymograph from simulations using the baseline parameters (Fig. 8 B). This is because the relatively fast kinetics of binding coupled to the diffusion of the free species within the droplet allows the droplet to quickly equilibrate with the external Fluor. Thus, for the common case where binding kinetics within the condensate are fast, the half bleach experiment may not readily distinguish between a liquid and gel state of the condensate matrix. In contrast, there is a qualitative difference between the liquid and gel condensate TotalF (=Fluor + FluorB) kymographs when the binding kinetics are slow (Fig. 8, D and E). This is because, for the gel simulation (Fig. 8 E), where the binding sites have 0 diffusion, the slow off rate preserves the sharp postbleach boundary between the levels of FluorB (the bound fluorescent species) in the two halves of the droplet, even as the level of Fluor (the unbound fluorescent species) is equilibrated between the external pool and droplet. (Importantly, in all these figures we only display the simulation results for TotalF because that is equivalent to the experimental observable; however, all the individual species can be just as readily be visualized in the VCell simulation results and are helpful to understand the model behavior.) This analysis shows again that both binding kinetics and diffusion of all diffusible species need to be considered in interpreting FRAP experiments. All these simulation results, together with 20 others representing other parameter combinations, are available in the Application “Large Liquid Droplet Image-based half bleach” within VCell BioModel “FRAP Condensate Droplet”; also included among these are simulations where a 10-fold lower diffusion coefficient within a 0.5 μm peripheral shell models an interfacial diffusion barrier (cf. Fig. 7 B); such a barrier has been invoked to explain experimental half-droplet bleaching results (46).

Figure 8.

Analysis of half bleach simulations of gel versus liquid condensates for an 8 μm diameter droplet. (A) Projection image of a 3D simulation immediately postbleach. The yellow line along the diameter indicates the position of the kymographs in (B–E). All the kymographs are from the central slice through the 3D simulation. (B) BinderD = 0.1 μm²/s, DropletD = 1 μm²/s, K_f = 0.025 μM⁻¹ s⁻¹. (C) BinderD = 0, DropletD = 1 μm²/s, K_f = 0.025 μM⁻¹ s⁻¹. (D) BinderD = 0.1 μm²/s, DropletD = 1 μm²/s, K_f = 0.00025 μM⁻¹ s⁻¹. (E) BinderD = 0, DropletD = 1 μm²/s, K_f = 0.00025 μM⁻¹ s⁻¹. Simulations can be found in VCell BioModel “FRAP Condensate Droplet” in the Application “Large Liquid Droplet Image-based half bleach.” Videos S11 and S12 correspond to center slices for the conditions in 8 B and 8 E. To see this figure in color, go online.

Discussion

In this work, we show that numerical solutions to partial differential equations can help guide the analysis of the reaction-diffusion dynamics revealed by FRAP experiments. We were motivated to create these mathematical models because analytical solutions or numerical parameter estimation algorithms for derivation of diffusion coefficients apply only to idealized cell and bleached region geometries. If binding kinetics are also involved, there must additionally be a good separation between the timescales of diffusion and reaction rates. On the other hand, numerical solutions of partial differential equations can be obtained using experimentally derived cell geometries and bleaching parameters that match the FRAP experiment. They can also include models of any binding reaction kinetics involving the fluorescently labeled molecule. Determining the values of the diffusion and kinetic constants can then be accomplished by running parameter scans and comparing the simulation results to the experiments. Our results were presented for a wide range of parameter values; in practice, these can be iteratively narrowed to find the parameter set to best match the experimental results. The different simulations can also be used to determine the range of parameter values that can reliably bracket the experiment, given the experimental signal/noise and temporal and spatial resolution. Importantly, the models can simulate the outcomes of various potential experimental protocols, allowing the investigator to design the optimal experiment to probe the biological question being addressed. Of course, if the experiments cannot be made to fit the simulations, the hypotheses underlying the model may be incorrect. Forcing the reevaluation of hypotheses could actually produce new insights into the underlying biophysical mechanisms—arguably the most valuable possible outcome of a modeling project.

We examined membrane diffusion, diffusion in a volume, and diffusion coupled to binding. We first (Fig. 2) used a simple model of 2D diffusion in a plane to show that analysis of the simulation results with a well-established fitting method (36) can precisely recover the value of D that was input into the model, even when using different sized bleaching areas. However, when using more realistic finite geometries, the fitting method tends to somewhat overestimate D (Figs. 3 and 4), while it is not at all applicable to determining diffusion on a thin process (Fig. 4). Turning to diffusion with binding (Fig. 5), we showed how modeling can help to design the most effective FRAP experimental protocol to best differentiate diffusional rates from off rates when the Kd is also unknown.

For the case of liquid droplets (Figs. 6, 7, and 8), the additional process of diffusion of the condensate matrix must be dissected from intradroplet diffusion of the free fluorophore; we show how this can be accomplished by the use of two protocols: FRAP of the entire droplet (Figs. 6 and 7), and the analysis of kymographs from line scans across a half-bleached droplet (Fig. 8). Importantly, binding kinetics can have a profound effect on the patterns derived from these experiments, with a clear distinction between gel and liquid condensates only possible when binding is slow (Fig. 8). On the other hand, determining diffusion characteristics within liquid droplets can be complicated when off rates are slow (Fig. 6), but can be bracketed by comparing experimental results with the parameter scan simulations. We also show how comparing FRAP in small (Fig. 6 A) with large (Fig. 7 A) droplets can help to uncover the relative contributions of internal diffusion versus binding to the probe dynamics. Finally, a simulation (Fig. 7 C) where an external shell is given a 10-fold lower diffusion coefficient than the bulk of the liquid droplet shows how this can significantly increase the gradient of recovery from the exterior to the interior. So, once again, solution of the forward problem via appropriate models can offer a direct path toward understanding the biophysics of biomolecular condensates without requiring previous assumptions; indeed such assumptions have been shown to be unjustified (34,35).

The results described in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and in the supporting material are a very small fraction of all the simulation experiments that are openly available in the VCell models associated with this paper. For example, the “FRAP Condensate Droplet” BioModel contains an Application that simulates a FLIP experiment to explore the kinetics of Fluor dissociation from the droplet (see also Fig. S3). Many other simulation experiments exploring various cellular and bleaching geometries can be found in the VCell public BioModels: “FRAP_Cyt,” “FRAP_Membrane_Rel,” “FRAP Condensate Droplet,” and “FRAP_Cyt_Membrane_Binding.” Furthermore, all these simulation experiments are investigated through many individual simulations that extensively sample the parameter space. Overall, there are approximately 700 simulations results in these 4 BioModels.

While these various FRAP protocols and parameter scans are certainly extensive, they are not at all exhaustive. Still, we hope that these models can serve as a guide to simulating any kind of photobleaching experiment. Furthermore, there are issues associated with fluorescence microscopy that could be readily added to more accurately simulate an experiment. It would be straightforward, for example, to add a constant slow bleach process to these models to simulate “bleach while monitoring,” or to add a process to account for relief from self-quenching occurring during the bleach. For example, we recently published an analysis of photobleaching a membrane probe in Bacillus subtilis spores that required both bleaching during monitoring and unquenching reactions (49). In this case, appropriate control experiments were used to fit parameters for the bleaching during monitoring and unquenching reactions. There are also other features of VCell that may be exploited to produce realistic models of FRAP experiments. For example, the distribution of binding sites may be nonuniform; or, in the case of liquid droplets, there may be multiple droplets with variable size and shape throughout the cell. Images of these can be used in a VCell feature called “Field Data” to define the spatially heterogeneous distribution of initial concentrations and their diffusion coefficients. “Field Data” can also be used to create laser distributions for bleaching in the case where unusual optical conditions during bleaching preclude developing an appropriate expression to define the bleaching reaction. Fig. 5 used ImageJ to help analyze simulation results; VCell has some integration with ImageJ to help both automated incorporation of experimental data into models and more advanced analysis of simulation results. Finally, it is important to emphasize that the modeling techniques described here for FRAP may readily be applied to other photochemistry-based microscope experiments, including photoactivation of fluorescence (50), uncaging of signaling molecules (26), photoablation of labeled proteins (51), and optogenetic activation of signaling proteins (52).

Author contributions

Both L.M.L. and A.E.C. conceived the research, built the models, performed simulations, and wrote and edited the manuscript.

Editor: Anne Kenworthy.

Supporting material

Data S5. Complete XML code for the VCell BioModel "FRAP Condensate Droplet" used in this work

These models are accessible together will all the simulations in the VCell database.

Data S6. Complete XML code for the VCell BioModel "FRAP_Cyt" used in this work

These models are accessible together will all the simulations in the VCell database.

Data S7. Complete XML code for the VCell BioModel "FRAP_Membrane_Rel" used in this work

These models are accessible together will all the simulations in the VCell database

Data S8. Complete XML code for the VCell BioModel "FRAP_Cyt_Membrane_Binding" used in this work

These models are accessible together will all the simulations in the VCell database