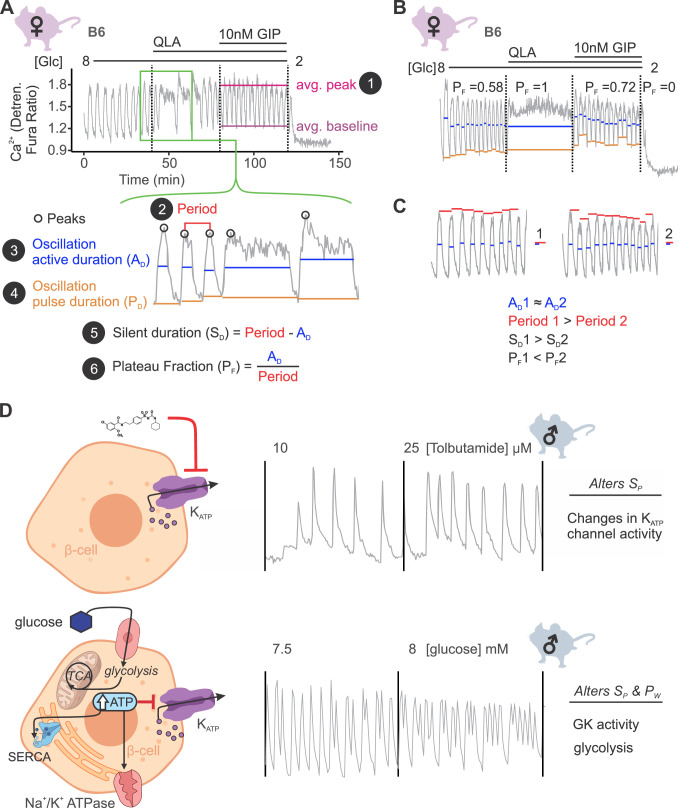
Figure 2. Ca²⁺ wave breakdown reveals mechanisms underlying Ca²⁺ responses.

(A) An example B6 female Ca²⁺ wave, showing that the islet oscillations can change in their average peak (1) and average baseline in response to different nutrients. Additionally, shifts in wave shape (green box) can be broken down into changes in time between peaks (period, 2), the time in the active phase (active duration, A_D, 3), and the length of the oscillation (pulse duration, P_D, 4). From these, the time inactive between oscillations (silent duration, S_D, 5), and the relative time in the active phase, or plateau fraction (P_F, 6), can be calculated. Each parameter can be changed by different underlying mechanisms. (B) For islets that plateaued, as in the example islet in 8G/QLA, they were assigned a plateau fraction of one and a period of zero. For islets that ceased to oscillate, such as the example islet in 2 mM glucose, they were assigned a plateau fraction of zero and a period of the time of measurement (40 min). (C) For trace 1 (left), which has a longer period (red bars) than trace 2 (right), but the same active duration (blue bars), the silent duration is greater and consequently the P_F is shorter, in contrast to the trace in (A) where the P_F increases between 8G and 8G/QLA are largely due to increases in A_D. (D) Changes in specific Ca²⁺ wave parameters can reflect different mechanisms in β-cells. For example, changing K_ATP activity pharmacologically (upper panels) predominantly increases P_F by altering S_D, whereas increasing glucose concentrations by elevating glucose or activating GK cause significant alterations in both A_D and S_D to increase P_F. Abbreviations: ‘[Glc]’ = ‘concentration of glucose in mM’; ‘GK’ = ‘glucokinase’.

Figure 2—figure supplement 1. Example of spectral density breakdown for Ca²⁺ traces.

(A) For the trace segment shown, the wave can be broken down into individual periodic waves (e.g. sine waves) of discrete amplitudes that, when added together, reproduce the trace. The frequency of each of these waves and its relative contribution to the overall trace signal is shown in (B), with frequency on the x axis and the spectral density, or the strength of each component signal, on the y axis. This was computed using scripts in R. The strongest two frequencies, denoted 1st and 2nd, respectively, are indicated. Related to Figure 2.