Abstract
The Bergman cyclization of (Z)-hexa-3-ene-1,5-diyne to form the aromatic diradical p-benzyne has garnered attention as a potential antitumor agent due to its relatively low cyclization barrier and the stability of the resulting diradical. Here, we present a theoretical investigation of several ionic extensions of the fundamental Bergman cyclization: electrocyclizations of the penta-1,4-diyne anion, hepta-1,6-diyne cation, and octa-1,7-diyne dication, leveraging the spin-flip formulation of the equation-of-motion coupled cluster theory with single and double substitutions (EOM-SF-CCSD). Though the penta-1,4-diyne anion exhibits a large cyclization barrier of +66 kcal mol–1, cyclization of both the hepta-1,6-diyne cation and octa-1,7-diyne dication along a previously unreported triplet pathway requires relatively low energy. We also identified the presence of significant aromaticity in the triplet diradical products of these two cationic cyclizations.
Introduction
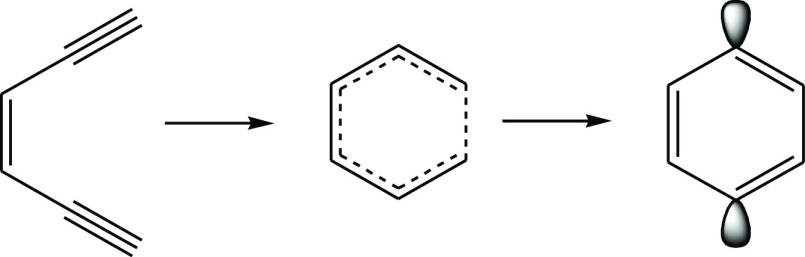
Bergman cyclization of (Z)-hexa-3-ene-1,5-diyne has been studied as a model for generating diradical p-benzyne-containing antitumor therapeutics.1−4 The DNA degradation activity is expected to occur upon excitation of the ground state diradical singlet to the decoupled triplet, which abstracts hydrogen atoms inducing cell death.5 This reaction has been well studied experimentally6−11 and computationally12−35 (Scheme 1). It is not surprising that the activation barrier (28.2 kcal mol–1) for this rearrangement is relatively small, as it is an interrupted, stepwise, symmetry-allowed [2 + 2] electrocyclization reaction.17,36−40 More remarkable is that its thermodynamic cost is only 8.5 kcal mol–1; the low endothermicity is the result of aromatization and the inherent thermodynamic instability of multiple bonds.41 The latter is exemplified by the strainless reaction of three ethylenes to form cyclohexane, which has been shown both experimentally and theoretically to be exothermic by nearly 70 kcal mol–1. Similarly, the reaction of four acetylenes to form cyclooctatetraene is exothermic by 146 kcal mol–1.42
Scheme 1. Bergman Cyclization of (Z)-Hexa-3-ene-1,5-diyne Forming Cyclic Diradical p-Benzyne.
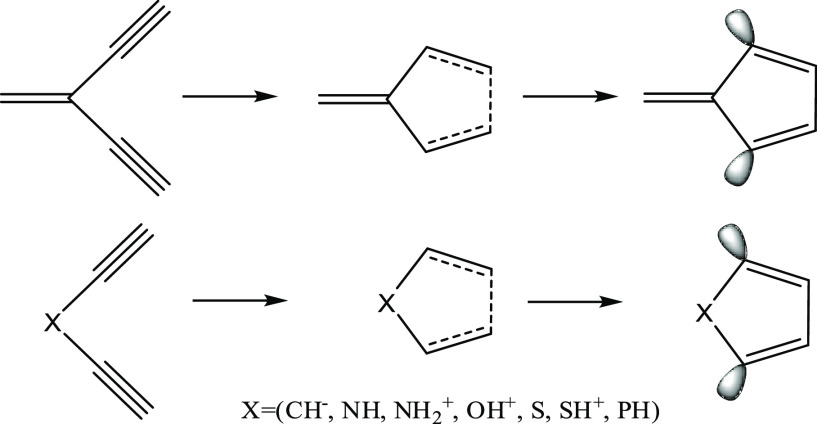
Kawatkar and Schreiner43 have shown that the aromatic driving force could be harnessed for the 1,5-cyclization of 3-substituted 1,4-pentadiynes. Because the radical orbitals are coplanar with the ring and are therefore unavailable for conjugation in the π system, the two “extra” electrons in this case are provided by a double bond at the 3-position or from a 3-substituent that contains lone pairs in conjugation with the π system (Scheme 2). Both the heteroatom and substituent effects were investigated in their study, which found that the ideal substituent X should be σ-withdrawing and π-donating, and the lowest cyclization barrier (for X=OH+) was computed to be +34.9 kcal mol–1 at the BLYP/6-31G* level of theory. Clearly, in order to experimentally harness the aromatic driving force for these cyclizations, enediynes must be designed with lower cyclization barriers and more favorable energies of reaction.
Scheme 2. Extensions of the Bergman Cyclization to Functionalized 1,4-Pentadiynes by Kawatkar and Schreiner43 .
Reproduced from ref (43). Copyright 2002 American Chemical Society.
Aromaticity as a driving force was explored by Wu and co-workers. The gain of aromaticity and electronic complementarity has been shown to drive base pair selectivity.44 The same group has also shown that changes in aromaticity can affect hydrogen-bonding of π-conjugated heterocycles45 and influence the properties of annulated rings46 and other species.47,48
Bergman cyclizations of ionic species have not been fully explored either experimentally or computationally. Alabugin and co-workers have explored 1,5- and 1,6-cyclization in radical anions12 and harnessed aromaticity in driving cyclization in five-centered, six-electron anionic 5-endo species.40 Experimentally, the same group has reported an elegant and well-reasoned approach to Bergman cyclization of anionic enediynes by electron or hole injection.49
For the canonical Bergman cyclization, it has been suggested that bringing together the two acetylenic carbons to induce the formation of a new C–C bond contributes to a lowering of the activation energy.2 For cyclization to proceed, it has been proposed that the distance between terminal acetylenic carbons must fall within a “critical range” of approximately 2.9–3.4 Å, but no predictive relationship between this distance, the -yne orientation, and the activation energy has been demonstrated.50−52
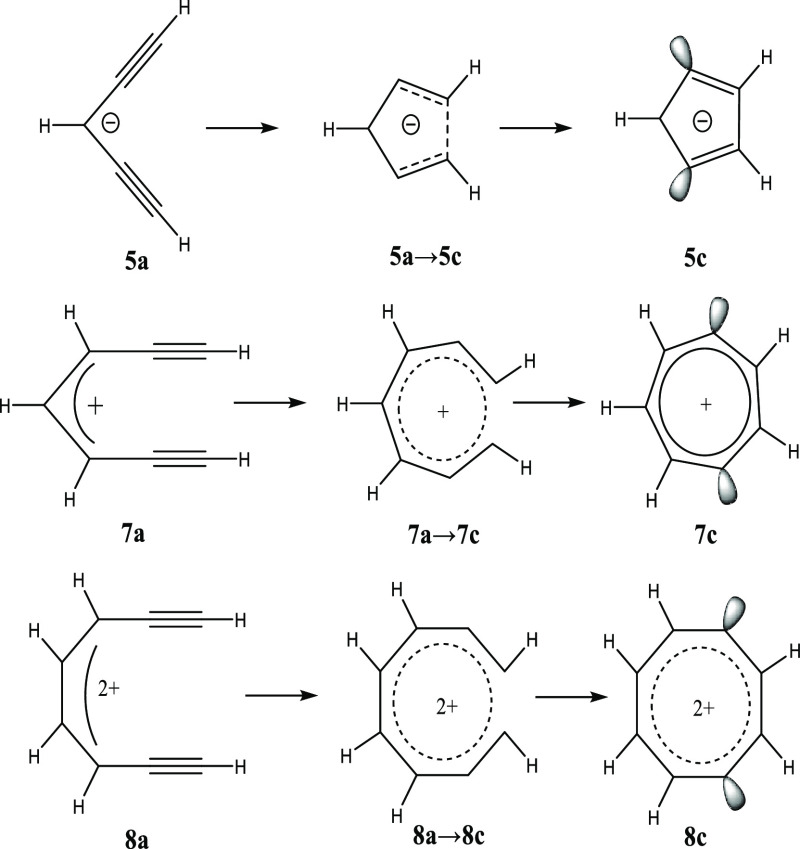
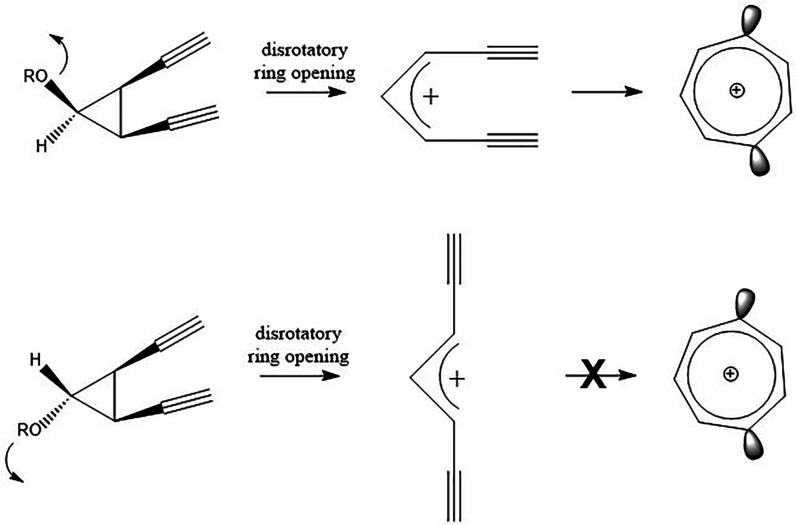
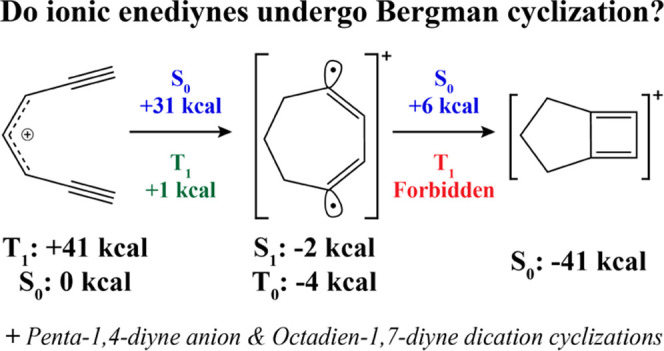
In this work, we explore the aromatic driving force for ionic extensions of the Bergman cyclization (Scheme 3) and investigate the electronic structures and energetics of cyclization specifically for penta-1,4-diyn-3-ide (Scheme 3, top), (Z)-hepta-4-en-1,6-diyn-3-ylium (Scheme 3, middle), and octa-3,5-dien-1,7-diyne-4,5-diylium (Scheme 3, bottom). In the following, we will abbreviate these IUPAC names to 5a → penta-1,4-diyne anion; 7a → hepta-1,6-diyne cation, and 8a → octa-1,7-diyne dication. To the best of our knowledge, no theoretical studies of the cationic Bergman-type cyclization have been reported previously, and these results yield interesting insights into the bonding of aromatic diradicals. Furthermore, the cyclization of the hepta-1,6-diyne cation is of particular interest for possible drug design because (in principle) it could be selectively obtained from the disrotatory ring-opening of a cyclopropyl precursor containing a stereospecifically placed leaving group, as shown in Scheme 4.
Scheme 3. Ionic Variations on the Bergman Cyclization.
Scheme 4. Generation of the Hepta-1,6-diyne Cation (7a) via the Disrotatory Ring Opening of a Cyclopropyl Precursor.
Results and Discussion
We performed geometry optimizations of all reactants, transition states, and products in the cyclizations shown in Scheme 3 using the spin-flip (SF) formulation of equation-of-motion coupled cluster theory with single and double substitutions (EOM-SF-CCSD)53−62 along with the correlation-consistent polarized-valence double-ζ (cc-pVDZ) basis set. The SF approach allows for an accurate characterization of multiconfigurational systems by optimizing the single-reference triplet state and then performing spin flip transitions to determine the energy and orbital occupations of the resulting singlet states (see Section S1A in the Supporting Information for additional details). By fully characterizing the energetic profile of each Bergman-type cyclization presented in Scheme 3, we determined that the cyclization of the penta-1,4-diyne anion (Scheme 3, top) has a significant cyclization barrier of +66 kcal mol–1, which is thermally inaccessible under physiological conditions. We will therefore restrict our discussion to the cyclizations of the hepta-1,6-diyne cation and octa-1,7-diyne dication (Scheme 3, middle and bottom, respectively); for a full analysis of the cyclization of the penta-1,4-diyne anion, refer to Section SIIA in the Supporting Information.
Cyclization of the Hepta-1,6-diyne Cation
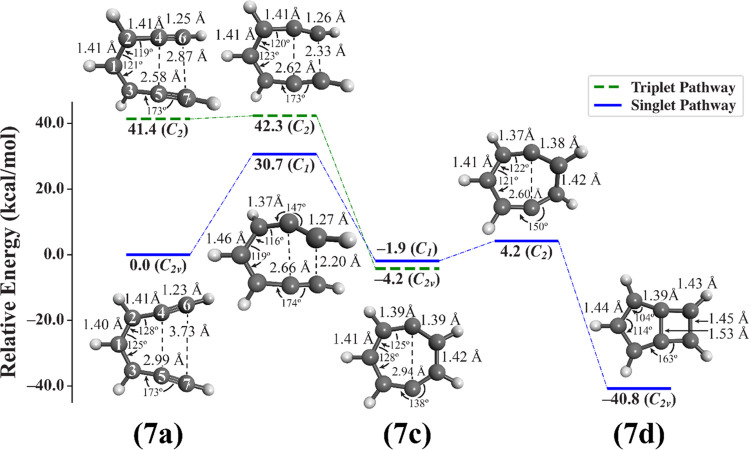
The reaction energy profile for the singlet cyclization of the hepta-1,6-diyne cation (blue solid lines) is shown in Figure 1 (atom numbering was overlaid upon the inset structure for 7a). The reactant 7a adopts a planar, C2v-symmetric structure in the X1A1 state, with slightly bent triple bonds (∠357 = ∠246 ≈ 173°). The equivalence of C1–C2 and C1–C3 bond lengths at ∼1.40 Å suggests that the positive charge of 7a is well distributed among the central carbons C3–C1–C2. The geometry of 7a, along with its C2v symmetry, can be understood by examining the molecular orbitals (MOs) for this species, which are visualized in Figure S15a–c in the Supporting Information. The unrestricted highest-occupied molecular orbital (HOMO), lowest-unoccupied molecular orbital (LUMO), and LUMO + 1 in both α and β manifolds for the X1A1 state of the hepta-1,6-diyne cation (Figure S4b) resemble the idealized π molecular orbitals for the allyl system almost perfectly (Figure S4a), even though these orbitals are canonical (i.e., delocalized). Furthermore, the 2b2 orbital—resembling the idealized, totally bonding π1 orbital in the allyl system—is doubly occupied in this electronic state of 7a, leading to both the C3–C1–C2 bond length equalization and this species’ planarity.
Figure 1.
Reaction energy profile for singlet (solid blue lines) and triplet (dashed green lines) cyclization pathways of the hepta-1,6-diyne cation (Scheme 3, middle). Energies of all species were computed relative to the singlet reactant 7a at the (SF-EOM)CCSD/cc-pVDZ level of theory, and geometries (structures inset) were optimized at these same levels of theory (for 7c, the singlet geometry is shown). For convenience, we also provide geometric parameters for interatomic distances R(1,2) = R(1,3), R(2,4) = R(3,5), R(4,6) = R(5,7), R(4,5), and R(6,7) (Å) and bond angles ∠213, ∠421 = ∠135, and ∠357 = ∠246 (deg) for each optimized geometry; atom numbers are superimposed on the inset structure 7a.
The distance between terminal acetylenic carbons C6···C7 of 7a is ∼3.7 Å, larger than the critical range of approximately 2.9–3.4 Å previously hypothesized to be necessary for cyclization to occur in the 6-membered Bergman cyclization.29,51,52 Even so, the cyclization barrier along the singlet pathway is only +30.7 kcal mol–1, closely resembling the cyclization barrier of +30.4 kcal mol–1 computed by Luxon et al. for the canonical Bergman cyclization.27 These are relatively low barriers, considering that cyclization proceeds via a complicated, multiconfigurational, multistate singlet pathway. (For more details, see discussion in Section SIA in the Supporting Information for electronic configurations and states formed by symmetry-adapted linear combinations thereof in two-level systems representative of the diradicals examined here.)
Along the singlet pathway shown in Figure 1, the transition state (7a → 7c) adopts a twisted, nonsymmetric (C1) structure, where the forming C6···C7 bond length is 2.2 Å. The formation of this bond generates 7c, a two-configurational, closed-shell singlet diradical with a planar, C1 structure which is nearly of C2v symmetry. Attempts to optimize the C2v7c structure were unsuccessful due to numerical instabilities present in the parallel version of the Q-Chem coupled cluster code, which can appear during geometry optimizations of structures with high symmetry.63 Regardless of the slightly nonsymmetric structure of the diradical product, this cyclization exhibits a total reaction energy of −1.9 kcal mol–1, compared to +5.8 kcal mol–1 computed by Luxon et al. at this level of theory for the canonical Bergman cyclization (value computed from those given in Table S3 in the Supporting Information of ref (27)). This increased stability of 7c versus p-benzyne is likely due to decreased ring strain in this 7-membered cyclic diradical versus the 6-membered p-benzyne.
In addition to the singlet pathway to form 7c, we have also identified a low-lying triplet pathway (Figure 1, dashed green bars with corresponding structures inset) which, once initiated from the 1 3B state of triplet 7a in C2 symmetry, proceeds through a transition state of the same symmetry to form a planar, C2v structure of 7c in the 3B2 state. Along this triplet surface, we optimized and frequency-confirmed all geometries using conventional coupled cluster theory with single and double substitutions (CCSD) where we access the high-spin triplet state directly rather than utilizing spin-flip excitations. For consistency with the EOM-SF-CCSD/cc-pVDZ treatment of species along the singlet pathway, these computations also utilized the same cc-pVDZ basis set and an unrestricted reference determinant.
Unlike the singlet ground state of reactant 7a, the triplet state adopts a twisted, C2-symmetric structure. The triple bonds in this structure deviate from linearity by 7° to a bond angle of ∠357 = ∠246 ≈ 173°; however, unlike for the singlet structure, the triple bonds orient out of the plane to increase the dihedral angle between the acetylenic termini to D(6,2,3,7) = 31°, from the 25° for dihedral angle D(4,2,3,5). As with the X1A1 state of 7a examined above, the geometric features of this twisted structure arise from the molecular orbitals occupied by this lowest-energy triplet state (1 3B), visualized in Figure S4c in the Supporting Information. This triplet state of 7a also exhibits three unrestricted molecular orbitals in both α and β manifolds resembling the idealized π system of the allyl cation; however, it singly occupies each of the 11b and 13a orbitals, which resemble the idealized totally bonding (π1) and nonbonding (π2) molecular orbitals of allene, respectively. By transferring an electron out of the totally π bonding 11b orbital into the π-nonbonding 13a orbital, the barrier to out-of-plane rotation is significantly reduced as compared to the X1A1 state of 7a, thereby allowing for this lowest-energy triplet to adopt a twisted conformation that reduces the overall Coulombic repulsion between alkyne moieties. Furthermore, this twisting allows the alkynyl π systems to rotationally decouple from the π system of the central allyl cation moiety, thereby permitting the nonlinearity of the triple bonds to orient themselves in such a way as to increase the distance between -yne termini such that D(6,2,3,7) > D(4,2,3,5). Even with this exaggerated twist, however, the central bond angle ∠213 of 121° in the 1 3B state of 7a leads to a C6···C7 distance of only 2.87 Å, nearly a full Ångström closer than that in the singlet state.
Thanks to the decreased distance between the acetylenic termini in the triplet structure of 7a, only minor geometric deformation is necessary to assume the structure of transition state 7a → 7c along the triplet pathway. Together with the ease of out-of-plane rotation facilitated by occupying the π-nonbonding molecular orbital of the central allyl cation moiety and reduced in-plane Coulombic repulsion between the alkyne termini, the triplet pathway has a low cyclization barrier of only +1 kcal mol–1. The structure for the triplet state of 7c, while able to be optimized within C2v symmetry, is geometrically similar to the singlet state with deviations of less than ±0.001 Å in C···C bond lengths and less than 0.2° in bond angles. The similarity in the molecular geometry of these states leads to a very small adiabatic singlet–triplet energy gap of +2.3 kcal mol–1, with the triplet being the ground state of 7c at this geometry (X3B2). This stands in contrast to p-benzyne, whose ground state is a two-configurational, closed-shell singlet (TCS).27 We have verified the X3B2 ground state of 7c by characterizing the energetic ordering of these states for 7c at both singlet-optimized C1 and triplet-optimized C2v geometries, provided in Table S1 in the Supporting Information, and determined that the X3B2 ground state of 7c is insensitive to both symmetry considerations and minor geometric perturbations. A triplet ground state for 7c may be due to a reduced through-bond coupling strength between radical centers in 7c versus p-benzyne, as there is only one intervening, ideally oriented 1,4 σ bonding pathway38,39 connecting the radical centers of 7c compared to two such connections in p-benzyne (for further details including the σ and σ* contributions to the overall wave function, see Section SIIC in the Supporting Information). Compared to the singlet state of 7a, the formation of the triplet state of 7c is only modestly exothermic, with a total cyclization energy of −4.2 kcal mol–1; however, this cyclization is extremely favorable on the triplet surface, with a total reaction energy of −45.6 kcal mol–1.
Interestingly, we have also determined that if 7c is generated in the singlet state, a bond may form between the radical centers to form bicyclic species 7d, as visualized in Figure 1. This symmetry-allowed intramolecular ring closure proceeds via a slightly twisted C2-symmetry transition state 7c → 7d whose minor geometric deformation affords another small activation barrier of +6.1 kcal mol–1. The resulting bicyclic product, 7d, adopts a planar, C2v structure, but without the bond length equalization present in the singlet and triplet structures of 7c. Even with the apparent loss of aromaticity, however, 7d is stabilized relative to 7c by a significant −38.9 kcal mol–1, displaying the dominant thermodynamic advantage of forming σ bonds. Due to this significant thermodynamic stability and low barrier to ring closure, we hypothesize that if diradical 7c were to be generated in its singlet state, it will be quickly and completely deactivated from being pharmacologically useful for H atom abstraction via the formation of 7d.
The thermodynamic favorability of the formation of 7c along the triplet pathway raises two questions: From where does this extraordinary stability originate? and Can this process be leveraged for pharmacological applications? Inspired by the generation of 7a in the singlet state from a cyclopropyl precursor via a disrotatory ring opening, we propose that the triplet pathway for the formation of 7c could be accessed via the conrotatory ring opening visualized in Scheme 5, which may be instantiated photochemically or via triplet sensitization.64−66 If 7a could be generated in its triplet state, then the formation of diradical 7c should proceed both quickly and completely, thanks to the combination of minimal barrier height and the high thermodynamic stability of 7c. This diradical should be relatively long-lived not only due to its thermodynamic stability but also because the ring closure of the triplet state of 7c to form 7d is spin-forbidden. Triplet 7c may also be accessed via an intersystem crossing from the singlet state. In the planar conformation of 7c, the spin–orbit (SO) coupling should be zero, according to El-Sayed’s rule.67 However, under real conditions, the molecule flexes and bends such that the SO coupling may be intermittently enabled due to mixing between σ- and π-electrons (as in 7c in Scheme 5).68 Although the barrier height separating singlet 7c from 7d is only +6.1 kcal mol–1, it may nevertheless lend 7c a sufficiently long lifetime to be able to undergo intersystem crossing. Taken together, these observations lead us to believe that the formation of triplet 7c may be experimentally relevant and worth further investigation (see ref (69) for a recent mini-review of photosensitizer agents and their action).
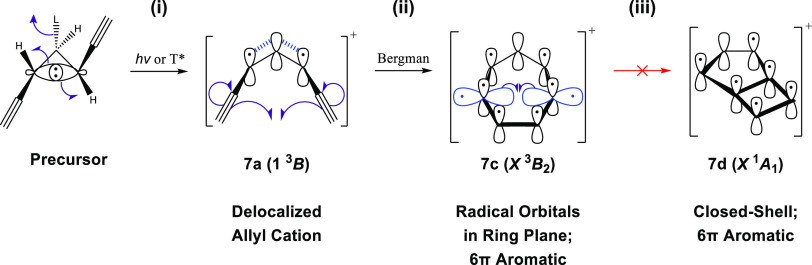
Scheme 5. Proposed Orbital Mechanism for the Stepwise Cyclization of 7c along the Triplet Pathway.
(i) Departure of a leaving group (L) and either photochemical excitation (hν) or triplet sensitization (T*) of a cyclopropyl precursor leads to conrotatory ring opening to form reactant 7a in its 1 3B state; (ii) Bergman-like interrupted [2 + 2] cycloaddition of the alkyne termini of 7a forms the cyclic diradical 7c in its X3B2 state; (iii) further intramolecular radical elimination to form bicyclic 7d in its X3A1 state is spin-forbidden.
To understand why 7c is so thermodynamically favorable, we have investigated the aromatic driving force for these cyclizations by performing isotropic NICS computations for singlet and triplet states of 7c as well as for 7d. These values are provided in Table 1, together with NICS analysis of benzene, p-benzyne, and both boat and chair conformers of cyclohexane for comparison. Based on the values for benzene and cyclohexane conformers, NICS values less than or equal to −8.0 indicate aromaticity, while those greater than or equal to −3.0 indicate nonaromaticity.
Table 1. NICS(−1, 0, +1) Indices for Cyclic Species 7c and 7d, as well as for p-Benzyne, Boat and Chair Cyclohexane, and Benzene.
| NICS index | boatb | chairb | benzeneb | p-benzynea | 7c (singlet)a | 7c (triplet)c | 7d (cyclopentyl)a | 7d (cyclobutyl)a |
|---|---|---|---|---|---|---|---|---|
| +1 | –1.7 | –2.0 | –10.2 | –19.0 | –10.9 | –11.1 | –9.8 | –11.6 |
| 0 | –2.4 | –2.0 | –8.2 | –28.6 | –11.5 | –10.8 | –5.5 | –1.2 |
| –1 | –3.1 | –2.0 | –10.2 | –19.0 | –10.9 | –11.1 | –9.8 | –11.6 |
BS-UB3LYP/6-311++G**.
B3LYP/6-311++G**.
UB3LYP/6-311++G**.
Using these qualitative ranges, both the singlet and triplet electronic states of 7c are aromatic, consistent with the bond-length equalization in these species noted earlier. Surprisingly, however, both cyclopentyl and cyclobutyl ring moieties of 7d appear to be aromatic despite the relative lack of bond-length equalization characteristic of typical aromatic species. The presence of aromaticity in the cyclobutyl moiety of 7d is doubly surprising because cyclobutadiene—the monocyclic analogue to the four-membered ring moiety of 7d—is known to be anti-aromatic! To investigate this further, we have computed isotropic deshielding values along an xy-scan connecting the two ring moieties’ geometric centers, raised 1 Å above the molecular plane (visualized in Figure S5 in the Supporting Information). These deshielding values (provided in Table S5 in the Supporting Information) demonstrate aromaticity along the entire scan, confirming that not only is the cyclobutyl moiety of 7d aromatic but also the entire molecule is aromatic.
Where, then, does this aromaticity originate? And how does it evade not only the seeming lack of bond-length equalization but also what appears to be an antiaromatic ring in the cyclobutadiene moiety? Fortunately, some good old-fashioned electron pushing is sufficient to explain this behavior. Provided in Scheme 5 is an orbital-based exposition of the cyclization profiled in Figure 1, beginning with the formation of 7a from its cyclopropyl precursor. After the departure of the leaving group from the precursor and conrotatory ring opening, there exist three unhybridized atomic 2pz orbitals on carbons C1, C2, and C3, over which two electrons are distributed leading to a delocalized cation (7a). Next, the diradical species 7c is formed by the interrupted [2 + 2] action of the Bergman cyclization, creating a π-network across the entire ring with 6 electrons occupying the seven contributing 2pz orbitals. Therefore, 7c conforms to the 4n + 2 rule, which conventionally defines aromaticity, so it should be no surprise that this species is so stable. Fortunately, the same picture also justifies the aromaticity observed in 7d. Key to this is the realization that the radical electrons localized on carbons C4 & C5 occupy orbitals that are perpendicular to the π system, within the plane of the ring. Thus, the formation of the new C4–C5 bond in 7d occurs without disturbing the out-of-plane 6π electrons that form the aromatic system. The source of the aromaticity in 7d is therefore the delocalization of these π electrons around the perimeter of the bicyclic system rather than any interaction between anti/aromaticity present in the individual ring moieties of this species. From a structural point of view, 7d can be thought of as a tropylium cation with a σ bond bisecting the seven-membered ring. The bridgehead σ bond (1.53 Å) is long because of the Mills–Nixon effect,70 which causes the four-membered ring in 7d to resemble a dimethylene cyclobutene more so than a cyclobutadiene.
Cyclization of the Octa-1,7-diyne Dication
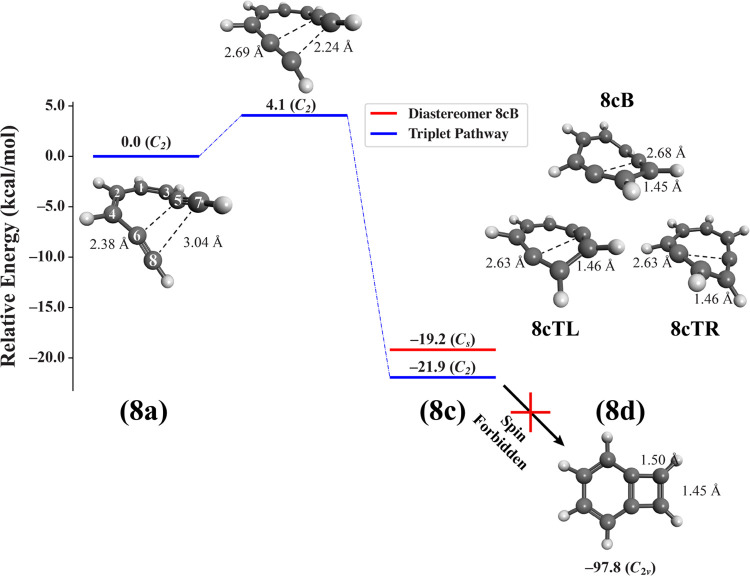
Unlike for the cyclization of the hepta-1,6-diyne cation explored above, all attempts to optimize the hypothetical singlet diradical product 8c proposed in Scheme 3 formed a closed bicyclic species 8d, analogous to that of 7d, which was stabilized relative to the singlet state of 8a by −73.6 kcal mol–1 (Table S4) This is not surprising given the enhanced conformational flexibility of the 8-membered ring and the tremendous thermochemical driving force associated with the formation of the new C5···C6 σ bond. Unfortunately, we were unable to identify transition state 8a → 8d, which would define this concerted pathway on the singlet surface. However, we did profile this cyclization using the frozen-string approach71 at the UCCSD/cc-pVDZ level of theory on the lowest singlet surface, which provides an approximate upper bound on the activation barrier of this pathway of +41.8 kcal mol–1. While the sizable exothermicity of the double cyclization process would cause any 8a present in the singlet state to thermodynamically convert to the pharmacologically inactive bicyclic species 8d, the approximate +41.8 kcal mol–1 barrier to this process is sufficiently high that we expect that the direct thermal conversion of 8a–d would be slow.
We also identified a triplet cyclization pathway, visualized in Figure 2 (blue lines). Much like the triplet pathway of the hepta-1,6-diyne cation cyclization, the triplet state of reactant 8a adopts a twisted, C2-symmetric structure, with acetylenic termini separated by ∼3.0 Å, a significantly smaller terminal distance than in the singlet geometry, where C7···C8 is separated by ∼4.7 Å. This C7···C8 distance decreases to ∼2.2 Å in the C2-symmetric transition state, with a barrier of only 4.1 kcal mol–1, before forming the diradical triplet 8c.
Figure 2.
Reaction energy profile for the triplet pathway (solid blue lines) of the cyclization of the octa-1,7-diyne dication (Scheme 3, bottom). Energies of all species were computed relative to adiabatic triplet reactant 8a at the UCCSD/cc-pVDZ level of theory, and geometries (structures inset) were optimized at these same levels of theory. For convenience, we provide geometric parameters for interatomic distances R(5,6) and R(7,8) (Å) for all species; atom numbering is superimposed over the inset structure for species 8a.
Unlike 7c, which adopted a single planar, C2v structure on the triplet surface, we have confirmed the presence of three distinct conformations of the triplet product 8c (structures inset in Figure 2): two inherently chiral, twisted conformations of C2 symmetry which we denote “twist-right” (8cTR) and “twist-left” (8cTL), as well as a boat-like conformer 8cB of Cs symmetry. The geometric variety of 8c is understandable given the increased conformational flexibility of the expanded 8-membered ring, and the inherent chirality of this molecule is due to the presence of two pseudoallene moieties surrounding each radical center within the ring. Indeed, 8cTL and 8cTR are nearly enantiomers of one another (geometric parameters agreeing to within ±0.1 Å), while 8cB is a near-diastereomer of these. As expected, 8cTL and 8cTR are isoenergetic to within 0.1 kcal mol–1, while 8cB is the least stable stereoisomer by nearly 3 kcal mol–1 (Figure 2, red line). It should be noted that the structures inset in Figure 2 demonstrate the formation of 8cTL; however, the isoenergetic pathway forming 8cTR simply proceeds through structures for 8a and 8a → 8c, which are of inverted symmetry from those shown in Figure 2.
The activation barrier for the 8a → 8c cyclization of +4.1 kcal mol–1 is notably smaller than the +35.6 kcal mol–1 barrier on the triplet surface of the conventional Bergman cyclization27 and only slightly larger than the +1 kcal mol–1 barrier to the formation of 7c on the triplet surface discussed above. A slightly higher cyclization barrier for the eight-membered system, relative to the seven-membered system, is likely due to Hammond’s postulate, supported by the fact that the C7···C8 distance in 8a must shorten by only 0.8 Å in order to assume the transition state structure 8a → 8c, compared with the equivalent C6···C7 distance in 7a needing to shorten by a mere 0.54 Å to assume the transition state structure of 7a → 7c. Interestingly, only transition states leading from left- and right-twisted conformations of 8a to the formation of 8cTL and 8cTR could be identified, whereas 8cB seems to not be able to form directly. Furthermore, no bona fide transition states could be identified for either 8cTL → 8cB or 8cB → 8cTR conformational transformations, making 8cB seemingly inaccessible from the other minima on the triplet surface, despite its energy being only +2.7 kcal mol–1 higher than that of its twisted diastereomers.
Regardless of which twisted conformer of 8c is formed, their stability relative to the reactant 8a, together with the fact that a subsequent ring-closure process to form 8d is spin-forbidden, leads to the conclusion that these are long-lived triplet diradicals. This stability could be due to the presence of aromaticity, as there are six π electrons to delocalize around the ring: two occupying the π orbitals of the butadiene dication moiety and another four left behind in the -ene units that remain after the Bergman cyclization. Unfortunately, the highly nonplanar and nonsymmetric nature of these species makes direct application of NICS to quantify the aromaticity in these systems unintuitive, as the locations for the probes used in NICS computations are typically defined relative to the ring plane, equidistant from all ring atoms. We have therefore generalized these conditions for placing NICS probes for symmetric, planar molecules to the nonsymmetric and nonplanar case, as discussed in Section SIC in the Supporting Information, and performed NICS computations to assess the presence of any aromaticity in the 8c triplet conformers, along with singlet 8d, in an identical manner to the computations described above for 7c and 7d. Presented in Table 2, NICS analysis indicates that both 8cTL and 8cTR are essentially aromatic, as all NICS indices for these twisted conformers hover around the qualitative cutoff value of −8.0 identified from the NICS indices of benzene presented in Table 1. On the other hand, the NICS indices for 8cB much more closely resemble those for the boat conformer of cyclohexane (for both 8cB and boat-cyclohexane, the +1 index is the one “riding” in the boat, whereas −1 is “below” the boat). This indicates that 8cB is essentially nonaromatic, in agreement with the finding that this is the least stabilized conformer of 8c. The closed-shell bicyclic species 8d is also aromatic, and an analogous xy-scan above the plane of the molecule reveals that, much like 7d, the aromaticity of 8d arises from delocalization around the perimeter of the ring rather than any aromaticity localized to an individual cyclic moiety. This global aromaticity is, therefore, the cause of the extraordinary stability of 8d.
Table 2. NICS(−1, 0, +1) Indices for Singlet 8d and Each Conformer of Triplet 8c.
| NICS index | 8cTLa | 8cBa | 8cTRa | 8d (cyclohexyl)b | 8d (cyclobutyl)b |
|---|---|---|---|---|---|
| +1 | –7.6 | –2.3 | –7.6 | –7.9 | –11.6 |
| 0 | –8.3 | –2.7 | –8.3 | –8.3 | +3.0 |
| –1 | –7.6 | –3.9 | –7.6 | –7.9 | –11.6 |
UB3LYP/6-311++G**.
B3LYP/6-311++G**.
Similar to the formation of triplet 7c, the aromatic stabilization of the twisted conformations of 8c together with the low reaction barrier on the triplet surface makes this cyclization of possible interest for experimental study. While significant molecular design work would be needed to build the 8a moiety into a biologically relevant scaffold in a synthetically accessible fashion, the vertical singlet–triplet gap for 8a in its singlet geometry of +47.2 kcal mol–1 (Table S4), or 2.0 eV, suggests that it may be useful for photodynamic therapies. This singlet–triplet gap corresponds to an excitation wavelength of ∼606 nm. While a direct S0 → T1 transition is spin-forbidden, the nonplanarity of 8a may allow for sufficient σ/π orbital mixing to produce spin–orbit coupling that could facilitate excitation to the triplet state. The penetration depth of visible light incident upon human skin increases with wavelength to a maximum of approximately 3.5 mm at λ = 1090 nm in the near-IR,72 before decreasing again for longer wavelengths due to the IR absorption of water73 (for a thorough review of light interactions with human tissue, see ref (74)). While not maximally penetrating, the 606 nm light required to vertically excite 8a from its X1A state to the 1 3B state falls within the so-called “therapeutic window” (see, e.g., Figure 3.6 in ref (74)), and indeed has been shown to penetrate up to approximately 1.5 mm of skin and 3 mm of mucosal tissue,72 making the triplet surface of 8a—and therefore the cyclization forming long-lived triplet diradicals 8c—of potential experimental interest.
Comparing the Energetics for All Cyclization Reactions
Provided in Table 3 are barriers and reaction energies of all cyclization reactions discussed here together with the same data for the canonical Bergman cyclization of (Z)-hexa-3-ene-1,5-diyne. We find that the barriers to cyclization for these enediynes on their singlet surfaces decrease consistently with the size of the ring produced by the cyclization. The experimentally determined barrier height for the canonical Bergman cyclization of (Z)-hexa-3-ene-1,5-diyne of +28.8 kcal mol–1 slightly bucks this trend; however, the electronic barrier height of +34.3 kcal mol–1 computed by Luxon et al.27 at the same level of theory used in this work is consistent with the trend demonstrated here for our ionic cyclizations.
Table 3. Relative Energies for Barrier Heights and Total Reaction Energies for the Bergman-like Cyclizations Examined in This Studya.
| elementary step | pathway | ΔE‡ (kcal mol–1) | ΔrE (kcal mol–1) |
|---|---|---|---|
| Penta-1,4-diyne Anion | |||
| 5a → 5c | OSS (Cs) | +108.6 | +106.5 |
| CSS (C2v) | +65.6 | +32.9 | |
| CSS (C1) | +21.8 | ||
| (Z)-Hexa-3-ene-1,5-diyne | |||
| theoryc | CSSb | +34.3 | +12.6 |
| tripletc | +32.9 | –35.9 | |
| experimentd,e,f | +28.2d | +8.5d or +13e | |
| Hepta-1,6-diyne Cation | |||
| 7a → 7c | singlet | +30.7 | –1.9 |
| triplet | +0.96 | –46.6 | |
| 7c → 7d | singlet | +6.1 | –38.9 |
| 7a → 7d (stepwise) | singlet | +30.7 | –40.8 |
| Octa-1,7-diyne Dication | |||
| 8a → 8cTL | triplet | +4.1 | –21.9 |
| 8a → 8d | singlet | +41.8f | –73.9 |
All barriers and reaction energies are adiabatic on their surfaces and were computed at the (SF-)UCCSD/cc-pVDZ level of theory for singlet and triplet pathways, respectively. Also included for comparison are theoretical and experimental estimates for the cyclization barrier and reaction energy of the canonical Bergman cyclization of (Z)-hexa-3-ene-1,5-diyne.
Relative energies constructed from absolute electronic energies computed at the SF-CCSD/cc-pVDZ level of theory with an unrestricted reference wave function, taken from Table S3 and in the Supporting Information of ref (22).
Relative energies constructed from absolute electronic energies computed at the CCSD/cc-pVDZ level of theory with an unrestricted reference wave function, taken from Table S7 and in the Supporting Information of ref (22).
Value taken from Figure 4 in ref (5).
Value taken from eq 10a in ref (75).
Approximate upper bound to this cyclization barrier estimated along a frozen-string reaction pathway71 constructed along the lowest singlet surface and computed at the CCSD/cc-pDVZ level of theory using a restricted reference wave function.
In the larger systems (7- and 8-membered), the diradicals undergo a highly exothermic radical recombination to form a new σ bond. That recombination is hindered if the ring is small (i.e., p-benzyne); however, if the ring is larger, the recombination is easier, as 7d and 8d demonstrate.
Interestingly, the cyclization energies on the triplet surface for both the hepta-1,6-diyne cation and octa-1,7-diyne dication are both smaller than on their respective singlet surfaces—with the cyclization barrier of the hepta-1,6-diyne cation nearly nonexistent at only +1 kcal mol–1 due primarily to the fact that smaller geometric distortions are needed for each of the triplet reactants of these cyclizations to assume their transition state geometry than for their singlet counterparts.
A similar trend is observed for reaction energies on the singlet surface: with increasing ring size, the cyclization becomes progressively more thermodynamically favorable. Indeed, even though the cyclization energies for the penta-1,4-diyne anion and (Z)-hexa-3-end-1,5-diyne are endothermic, the singlet cyclization of the hepta-1,6-diyne cation is exothermic by −1.9 kcal mol–1. Unfortunately, the singlet cyclizations of both hepta-1,6-diyne cation and octa-1,7-diyne dication both lead to the formation of closed-shell bicyclic species, which, thanks to their global aromaticity, are so thermodynamically stable that we expect any formation of cyclic diradical products along these singlet pathways would be inactivated. On the other hand, the triplet cyclization pathways are both exothermic by −46.6 and −21.9 kcal mol–1 for the hepta-1,6-diyne cation and octa-1,7-diyne dication, respectively, thanks to the aromaticity present in their cyclic diradical products. Additionally, these triplet diradicals are spin-forbidden from further cyclizing to form the inactive bicyclic species, which we hypothesize will make these species long-lived and, therefore, potentially attractive for further study.
Conclusions
We have characterized the energetics and aromatic driving force for Bergman-type cyclizations of ionic enediyne precursors, namely, the penta-1,4-diyne anion, the hepta-1,6-diyne cation, and the octa-1,7-diyne dication using high-level quantum chemical computations. While the 5-membered anionic system does indeed form a cyclized diradical, the energetic barrier to cyclization on the singlet surface is significantly large. We also see the formation of a diradical for the 7-membered cationic system, with a barrier to cyclization (∼31 kcal mol–1) comparable to the canonical 6-membered enediyne. We were unable to identify a diradical Bergman cyclization product for the octa-1,7-diyne dication on the singlet surface. On the triplet surfaces, both the hepta-1,6-diyne cation and octa-1,7-diyne dication enjoy small cyclization barriers of only +0.96 and +4.1 kcal mol–1, and exothermic reaction energies of −46.6 and −21.9 kcal mol–1, respectively. The exothermicity exhibited by these cationic Bergman cyclizations on the triplet surface is due to the presence of significant aromaticity, which we have quantified computationally via NICS analysis and justified with orbital arguments. Although we identified a pathway that would quench the diradicals of these 7- and 8-membered cyclizations on the singlet surface, the transformation of diradical to bicyclic σ bond formation is spin-forbidden when the diradicals are generated in their triplet states, making them both long-lived and thermodynamically stable.
Methods
We performed geometry optimizations of all reactants, transition states, and products using Q-Chem 5.4.1. We utilized the spin-flip formulation of equation-of-motion coupled cluster theory with single and double substitutions (EOM-SF-CCSD)53−62 together with the correlation-consistent polarized-valence double-ζ (cc-pVDZ) basis set. Each optimized geometry was verified as a true minimum (for reactants and products) or first-order saddle point (for transition states) on the potential energy surface at this same level of theory via frequency analysis. All spin-flip computations leveraged an unrestricted, high-spin reference determinant; a thorough discussion of the theoretical background and practical advice for performing spin-flip coupled cluster computations is provided in Section SIA in the Supporting Information (see Associated Content for further details). While spin contamination can be an issue for unrestricted wave functions, and even more so for excited states based on unrestricted references, we have only observed minor spin contamination in our computations (see, e.g., ⟨S2⟩ values provided in Tables S2–S4 in the Supporting Information).
In addition to quantitatively characterizing the energetics of these cyclization processes, we also examined the aromaticity in the diradical products as a possible thermodynamic driving force for these reactions. Though taught in every introductory organic chemistry classroom, aromaticity is, itself, not easy to define.76 One metric we have chosen to use is NICS,77 which in its simplest formulation associates aromaticity with the negative value of the isotropic magnetic shielding computed at a point in space—either within or nearby a ring moiety in the molecule of interest—using a “probe atom” (i.e., an atom with no basis functions or nuclear charge). In its original incarnation, the NICS probe was placed at a central point within the ring, equidistant from all ring atoms,77 an approach now denoted NICS(0). Further probes may be placed 1 Å above and below the plane of the ring, similarly equidistant from all ring atoms, which are denoted NICS(+1) and NICS(−1), respectively. Taken together, these so-called “isotropic” NICS computations are simple, which has led to their popularity as an index of aromaticity, despite some well-known limitations.78,79
Due to their reduction of a molecule’s overall aromaticity to a single value computed for a particular point in space, these isotropic NICS indices are very sensitive to the choice of probe location. Unlike conventional aromatic molecules, which are both highly symmetric and perfectly planar, several of the cyclic species examined here are neither planar nor symmetric; therefore, there exist no unique points equidistant to all ring atoms, and the notions of “above” or below the ring are also ill-defined. To address this complication, we place the NICS(0) probe at the ring’s non-mass-weighted geometric centroid, and NICS(±1) probes 1 Å in either direction from that centroid along the ring’s principal moment of inertia, thereby uniquely defining reproducible probe locations (see Section SIB and Figure S2 in the Supporting Information for further details).
We have computed isotropic NICS values for all cyclic species in this work using the Gaussian16 program80 at the unrestricted, broken-symmetry BS-UB3LYP/6-311++G** level of theory, using the molecular geometries optimized at the EOM-SF-CCSD/cc-pVDZ level of theory using Q-Chem. This symmetry-breaking approach is necessary to describe the electron density of diradical singlets with reasonable accuracy, by mixing the highest-occupied and lowest-unoccupied Kohn–Sham orbitals.81,82
Acknowledgments
This work was supported by awards from the National Science Foundation (C.A.P.: CHE-1800014, CHE-0211577, CHE-0116435, and CHE-0521063) and the Department of Energy (Grant DE-SC0001093). C.A.P. acknowledges the Donors of the American Chemical Society Petroleum Research Fund and the Thomas F. and Kate Miller Jeffress Memorial Trust for partial support of this work. C.A.P. also acknowledges support from the Camille and Henry Dreyfus Foundation through receipt of a Henry Dreyfus Teacher-Scholar Award. E.B.W. and A.L. acknowledge support from the Arnold and Mabel Beckman Foundation through receipt of Beckman Scholar awards. E.B.W. also acknowledges the Howard Hughes Medical Institute through receipt of an HHMI Undergraduate Summer Fellowship. M.Z. acknowledges the Merck/AAAS Undergraduate Summer Research Program and the Pratchett Foundation for summer fellowships. S.W. and S.A.M.-G. acknowledge summer support from the University of Richmond Integrated and Inclusive Science program, and the School of Arts & Sciences Undergraduate Research Committee. S.A.M.-G. also acknowledges summer support from the Puryear-Topham-Pierce-Gupton endowment from the Department of Chemistry at the University of Richmond. The authors thank Dr. Edward Sherer and Professor Judy Wu for useful discussions, and Dr. Evgeny Epifanovsky, Dr. Kuan-Yu Liu, and Dr. Shannon Houck for technical assistance. They thank George Flanagin for computational support. Computational resources were provided, in part, by the MERCURY supercomputer consortium under NSF grants CHE-0116435 and CHE-0521063.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.3c06691.
Zipped archive of molecular geometries for all stationary-point structures identified herein, each in plain-text XYZ format; additional theoretical background for diradical systems and the spin-flip approach; development of a general approach for placing NICS probes for nonsymmetric and nonplanar molecules; and additional tables, figures, and analysis (PDF)
Author Present Address
⊥ Wuhan Institute of Physics and Mathematics, Innovation Academic for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan, Hubei 430071, China
Author Present Address
# Department of Chemistry and Biochemistry, Ohio State University, Columbus, Ohio 43210, United States.
Author Present Address
∇ Eli Lilly and Company, Indianapolis, Indiana 46285, United States.
Author Present Address
○ Two Six Technologies, Arlington, Virginia 22203, United States.
Author Present Address
◆ Illumina, San Diego, California 92122, United States.
Author Present Address
¶ Fashion Institute of Technology, New York, New York 10001, United States.
Author Contributions
All authors have given approval to the final version of the manuscript.
The authors declare no competing financial interest.
Supplementary Material
References
- Nicolaou K. C.; Smith A. L. Molecular design, chemical synthesis, and biological action of enediynes. Acc. Chem. Res. 1992, 25 (11), 497–503. 10.1021/ar00023a003. [DOI] [Google Scholar]
- Nicolaou K. C.; Smith A. L.; Yue E. W. Chemistry and Biology of natural and designed enediynes. Proc. Natl. Acad. Sci. U.S.A. 1993, 90, 5881–5888. 10.1073/pnas.90.13.5881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borgers D. B.; Doyle T. E.. Enediyne Antibiotics as Antitumor Agents; Marcel Dekker: New York, 1995. [Google Scholar]
- Maeda H.; Edo K.; Ishida N.. Neocarzinostatin: The Past, Present and Future of an Anticancer Drug; Springer: New York, 1997. [Google Scholar]
- Roth W. R.; Hopf H.; Horn C. 1,3,5-Cyclohexatrien-1,4-diyl und 2,4-Cyclohexadien-1,4-diyl. Chem. Ber. 1994, 127 (9), 1765–1779. 10.1002/cber.19941270929. [DOI] [Google Scholar]
- Bergman R. G. Reactive 1,4-Dehydroaromatics. Acc. Chem. Res. 1973, 6, 25–31. 10.1021/ar50061a004. [DOI] [Google Scholar]
- Jones R. R.; Bergman R. G. p-Benzyne. Generation as an Intermediate in a Thermal Isomerization Reaction and Trapping Evidence for the 1,4-Benzenediyl Structure. J. Am. Chem. Soc. 1972, 94, 660–661. 10.1021/ja00757a071. [DOI] [Google Scholar]
- Wenthold P. G.; Hu J.; Squires R. R. o-, m-, and p-Benzyne Negative Ions in the Gas Phase: Synthesis, Authentication, and Thermochemistry. J. Am. Chem. Soc. 1996, 118 (47), 11865–11871. 10.1021/ja960663+. [DOI] [Google Scholar]
- Wenthold P. G.; Squires R. R. Biradical thermochemistry from collision-induced dissociation threshold energy measurements. Absolute heats of formation of ortho-, meta- and para-benzyne. J. Am. Chem. Soc. 1994, 116, 6401–6412. 10.1021/ja00093a047. [DOI] [PubMed] [Google Scholar]
- Wenthold P. G.; Squires R. R.; Lineberger W. C. Ultraviolet photoelectron spectroscopy of the o-, m-, and p-benzyne negative ions. Electron affinities and singlet-triplet splittings for o-, m-, and p-benzyne. J. Am. Chem. Soc. 1998, 120, 5279–5290. 10.1021/ja9803355. [DOI] [Google Scholar]
- McMahon R. J.; Halter R. J.; Fimmen R. L.; Wilson R. J.; Peebles S. A.; Kuczkowski R. L.; Stanton J. F. Equilibrium Structure of cis-Hex-3-ene-1,5-diyne and Relevance to the Bergman Cyclization. J. Am. Chem. Soc. 2000, 122 (5), 939–949. 10.1021/ja9934908. [DOI] [Google Scholar]
- Alabugin I. V.; Manoharan M. Radical-Anionic Cyclizations of Enediynes: Remarkable Effects of Benzannelation and Remote Substituents on Cyclorearomatization Reactions. J. Am. Chem. Soc. 2003, 125 (15), 4495–4509. 10.1021/ja029664u. [DOI] [PubMed] [Google Scholar]
- Chen W.-C.; Chang N.-y.; Yu C.-h. Density Functional Study of Bergman Cyclization of Enediynes. J. Phys. Chem. A 1998, 102, 2584–2593. 10.1021/jp973261c. [DOI] [Google Scholar]
- Clark A. E.; Davidson E. R. p-Benzyne Derivatives That Have Exceptionally Small Singlet-Triplet Gaps and Even a Triplet Ground State. J. Org. Chem. 2003, 68, 3387–3396. 10.1021/jo026824b. [DOI] [PubMed] [Google Scholar]
- Cramer C. J. Bergman, Aza-Bergman, and Protonated Aza-Bergman Cylizations and Intermediate 2,5-Arynes: Chemistry and Challenges to Computation. J. Am. Chem. Soc. 1998, 120, 6261–6269. 10.1021/ja9806579. [DOI] [Google Scholar]
- Crawford T. D.; Kraka E.; Stanton J. F.; Cremer D. Problematic p-benzyne: Orbitals instabilities, biradical character, and broken symmetry. J. Chem. Phys. 2001, 114, 10638–10650. 10.1063/1.1373433. [DOI] [Google Scholar]
- Galbraith J. M.; Schreiner P. R.; Harris N.; Wei W.; Wittkopp A.; Shaik S. A Valence Bond Study of the Bergman Cyclization: Geometric Features, Resonance Energy, and Nucleus-Independent Chemical Shift (NICS) Values. Chem. - Eur. J. 2000, 6 (8), 1446–1454. 10.1002/(SICI)1521-3765(20000417)6:83.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
- Gräfenstein J.; Hjerpe A. M.; Kraka E.; Cremer D. An Accurate Description of the Bergman Reaction Using Restricted and Unrestricted DFT: Stability Test, Spin Density, and On -Top Pair Density. J. Phys. Chem. A 2000, 104, 1748–1761. 10.1021/jp993122q. [DOI] [Google Scholar]
- Koga N.; Morokuma K. Comparison of biradical formation between enediyne and enyne-allene. Ab initio CASSCF and MRSDCI study. J. Am. Chem. Soc. 1991, 113 (6), 1907–1911. 10.1021/ja00006a006. [DOI] [Google Scholar]
- Kraka E.; Cremer D. Ortho-, meta-, and para-benzyne. A comparative CCSD(T) investigation. Chem. Phys. Lett. 1993, 216, 333–340. 10.1016/0009-2614(93)90105-A. [DOI] [Google Scholar]
- Kraka E.; Cremer D. CCSD(T) Investigation of the Bergman Cyclization of Enediyne. Relative Stability of o-, m-, and p-Didehydrobenzene. J. Am. Chem. Soc. 1994, 116, 4929–4936. 10.1021/ja00090a043. [DOI] [Google Scholar]
- Kraka E.; Cremer D. The para-Didehydropyridine, para-Didehydropyridinium, and Related Biradicals- A Contribution to the Chemistry of Enediyne Antitumor Drugs. J. Comput. Chem. 2001, 22 (2), 216–229. . [DOI] [Google Scholar]
- Lindh R.; Bernhardsson A.; Schutz M. Benzyne Thermochemistry: A benchmark ab initio study. J. Phys. Chem. A 1999, 103, 9913. 10.1021/jp991919b. [DOI] [Google Scholar]
- Lindh R.; Lee T. J.; Bernhardsson A.; Persson B. J.; Karlstrom G. Extended ab Initio and Theoretical Thermodynamics Studies of the Bergman Reaction and the Energy Splitting of the Singlet o-, m-, and p-Benzynes. J. Am. Chem. Soc. 1995, 117, 7186–7194. 10.1021/ja00132a019. [DOI] [Google Scholar]
- Lindh R.; Persson B. J. Ab Initio Study of the Bergman Reaction: the Autoaromatization of Hex-3-ene-1,5-diyne. J. Am. Chem. Soc. 1994, 116, 4963–4969. 10.1021/ja00090a047. [DOI] [Google Scholar]
- Lindh R.; Schutz M. Singlet Benzyne Thermochemistry: a CASPT2 study of the enthalpies of formation. Chem. Phys. Lett. 1996, 258, 409–415. 10.1016/0009-2614(96)00653-7. [DOI] [Google Scholar]
- Luxon A. R.; Orms N.; Kanters R.; Krylov A. I.; Parish C. A. An ab Initio Exploration of the Bergman Cyclization. J. Phys. Chem. A 2018, 122 (1), 420–430. 10.1021/acs.jpca.7b10576. [DOI] [PubMed] [Google Scholar]
- Navarro-Vazquez A.; Prall M.; Schreiner P. R. Cope Reaction Families: To be or not to be a diradical. Org. Lett. 2004, 6, 2981–2984. 10.1021/ol0488340. [DOI] [PubMed] [Google Scholar]
- Prall M.; Krüger A.; Schreiner P. R.; Hopf H. The Cyclization of Parent and Cyclic Hexa 1, 3 dien 5 ynes—A Combined Theoretical and Experimental Study. Chem. - Eur. J. 2001, 7 (20), 4386–4394. 10.1002/1521-3765(20011015)7:203.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- Schreiner P. R.; Navarro-Vazquez A.; Prall M. Computational Studies on the cyclizations of enediynes, enyne-allenes and related polyunsaturated systems. Acc. Chem. Res. 2005, 38, 29–37. 10.1021/ar020270h. [DOI] [PubMed] [Google Scholar]
- Stahl F.; Moran D.; von Schleyer R. P.; Prall M.; Schreiner P. R. Aromaticity of the Bergman, Myers-Saito, Schmittel, and directly related cyclizations of enediynes. J. Org. Chem. 2002, 67 (5), 1453–1461. 10.1021/jo015728s. [DOI] [PubMed] [Google Scholar]
- Wang E. B.; Parish C. A.; Lischka H. An extended multireference study of the electronic states of para-benzyne. J. Chem. Phys. 2008, 129, 044306 10.1063/1.2955744. [DOI] [PubMed] [Google Scholar]
- Wierschke S. G.; Nash J. J.; Squires R. R. A Multiconfigurational SCF and Correlation-Consistent CI Study of the Structures, Stabilities, and Singlet-Triplet Splittings of o-, m-, and p-Benzyne. J. Am. Chem. Soc. 1993, 115, 11958–11967. 10.1021/ja00078a038. [DOI] [Google Scholar]
- Dong H.; Chen B.-Z.; Huang M.-B.; Lindh R. The bergman cyclizations of the enediyne and its N-substituted analogs using multiconfigurational second-order perturbation theory. J. Comput. Chem. 2012, 33 (5), 537–549. 10.1002/jcc.22889. [DOI] [PubMed] [Google Scholar]
- Clark A. E.; Davidson E. R.; Zaleski J. M. UDFT and MCSCF Descriptions of the Photochemical Bergman Cyclization of Enediynes. J. Am. Chem. Soc. 2001, 123 (11), 2650–2657. 10.1021/ja0039987. [DOI] [PubMed] [Google Scholar]
- Alabugin I. V.; Manoharan M. Reactant destabilization in the Bergman cyclization and rational design of light-and pH-activated enediynes. J. Phys. Chem. A 2003, 107 (18), 3363–3371. 10.1021/jp026754c. [DOI] [Google Scholar]
- Brzostowska E. M.; Hoffmann R.; Parish C. Tuning the Bergman Cyclization by Introduction of Metal Fragments at Various Positions of the Enediyne. MetallaBergman Cyclizations. J. Am. Chem. Soc. 2007, 129, 4401–4409. 10.1021/ja068884v. [DOI] [PubMed] [Google Scholar]
- Hoffmann R. Interaction of Orbitals through space and through bonds. Acc. Chem. Res. 1971, 4, 1–9. 10.1021/ar50037a001. [DOI] [Google Scholar]
- Hoffmann R.; Imamura A.; Hehre W. Benzynes, dehydroconjugated molecules, and the interaction of orbitals separated by a number of intervening sigma bonds. J. Am. Chem. Soc. 1968, 90, 1499–1509. 10.1021/ja01008a018. [DOI] [Google Scholar]
- Gilmore K.; Manoharan M.; Wu J. I. C.; Schleyer P. v. R.; Alabugin I. V. Aromatic Transition States in Nonpericyclic Reactions: Anionic 5-Endo Cyclizations Are Aborted Sigmatropic Shifts. J. Am. Chem. Soc. 2012, 134 (25), 10584–10594. 10.1021/ja303341b. [DOI] [PubMed] [Google Scholar]
- Ploshnik E.; Danovich D.; Hiberty P. C.; Shaik S. The Nature of the Idealized Triple Bonds Between Principal Elements and the σ Origins of Trans-Bent Geometries—A Valence Bond Study. J. Chem. Theory Comput. 2011, 7 (4), 955–968. 10.1021/ct100741b. [DOI] [PubMed] [Google Scholar]
- Burgess D. R., Jr.Thermochemical Data. In NIST Chemistry WebBook, NIST Standard Reference Database; Linstrom P. J.; Mallard W. G., Eds.; National Institutes of Standards and Technology: Gaithersburg, MD, 2022. [Google Scholar]
- Kawatkar S. P.; Schreiner P. R. Cycloaromatization of 1,4-Pentadiynes: A Viable Possibility?. Org. Lett. 2002, 4 (21), 3643–3646. 10.1021/ol0266424. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Wu C.-H.; Wu J. I. C. Why do A·T and G·C self-sort? Hückel aromaticity as a driving force for electronic complementarity in base pairing. Org. Biomol. Chem. 2019, 17 (7), 1881–1885. 10.1039/C8OB01669K. [DOI] [PubMed] [Google Scholar]
- Kakeshpour T.; Wu J. I.; Jackson J. E. AMHB: (Anti)aromaticity-Modulated Hydrogen Bonding. J. Am. Chem. Soc. 2016, 138 (10), 3427–3432. 10.1021/jacs.5b12703. [DOI] [PubMed] [Google Scholar]
- Berionni G.; Wu J. I. C.; Schleyer P. v. R. Aromaticity Evaluations of Planar [6]Radialenes. Org. Lett. 2014, 16 (23), 6116–6119. 10.1021/ol5029699. [DOI] [PubMed] [Google Scholar]
- Wu J. I.; Karas L. J.. Antiaromaticity: A Brief History, Concepts and Applications. In Aromaticity Modern Computational Methods and Applications; Fernandez I., Ed.; Elsevier, 2021; Chapter 10. [Google Scholar]
- Barker J. E.; Price T. W.; Karas L. J.; Kishi R.; MacMillan S. N.; Zakharov L. N.; Gómez-García C. J.; Wu J. I.; Nakano M.; Haley M. M. A Tale of Two Isomers: Enhanced Antiaromaticity/Diradical Character versus Deleterious Ring-Opening of Benzofuran-fused s-Indacenes and Dicyclopenta[b,g]naphthalenes. Angew. Chem., Int. Ed. 2021, 60 (41), 22385–22392. 10.1002/anie.202107855. [DOI] [PubMed] [Google Scholar]
- Peterson P. W.; Shevchenko N.; Breiner B.; Manoharan M.; Lufti F.; Delaune J.; Kingsley M.; Kovnir K.; Alabugin I. V. Orbital Crossings Activated through Electron Injection: Opening Communication between Orthogonal Orbitals in Anionic C1–C5 Cyclizations of Enediynes. J. Am. Chem. Soc. 2016, 138 (48), 15617–15628. 10.1021/jacs.6b08540. [DOI] [PubMed] [Google Scholar]
- Prall M.; Kruger A.; Schreiner P. R.; Hopf H. The cyclization of parent and cyclic hexa-1,3-dien-5-ynes—A combined theoretical and experimental study. Chem. - Eur. J. 2001, 7, 4386–4394. 10.1002/1521-3765(20011015)7:203.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- Schreiner P. R. Monocyclic Enediynes: Relationships between Ring Sizes, Alkyne Carbon Distances, Cyclization barriers, and Hydrogen Abstraction Reactions. Singlet - Triplet Separations of Methyl - Substituted p - benzynes. J. Am. Chem. Soc. 1998, 120, 4184–4190. 10.1021/ja973591a. [DOI] [Google Scholar]
- Snyder J. P. Monocyclic Enediyne Collapse to 1,4-Diyl Biradicals: A Pathway under Strain Control. J. Am. Chem. Soc. 1990, 112, 5367–5369. 10.1021/ja00169a064. [DOI] [Google Scholar]
- Bernard Y. A.; Shao Y.; Krylov A. I. General formulation of spin-flip time-dependent density functional theory using non-collinear kernels: Theory, implementation, and benchmarks. J. Chem. Phys. 2012, 136 (20), 204103 10.1063/1.4714499. [DOI] [PubMed] [Google Scholar]
- Krylov A. I. Size-consistent wave functions for bond-breaking: the equation-of-motion spin-flip model. Chem. Phys. Lett. 2001, 338 (4–6), 375–384. 10.1016/S0009-2614(01)00287-1. [DOI] [Google Scholar]
- Krylov A. I. Spin-flip configuration interaction: an electronic structure model that is both variational and size-consistent. Chem. Phys. Lett. 2001, 350 (5–6), 522–530. 10.1016/S0009-2614(01)01316-1. [DOI] [Google Scholar]
- Krylov A. I. Spin-Flip Equation-of-Motion Coupled-Cluster Electronic Structure Method for a Description of Excited States, Bond Breaking, Diradicals, and Triradicals. Acc. Chem. Res. 2006, 39 (2), 83–91. 10.1021/ar0402006. [DOI] [PubMed] [Google Scholar]
- Krylov A. I.; Sherrill C. D. Perturbative corrections to the equation-of-motion spin–flip self-consistent field model: Application to bond-breaking and equilibrium properties of diradicals. J. Chem. Phys. 2002, 116 (8), 3194–3203. 10.1063/1.1445116. [DOI] [Google Scholar]
- Levchenko S. V.; Krylov A. I. Equation-of-motion spin-flip coupled-cluster model with single and double substitutions: Theory and application to cyclobutadiene. J. Chem. Phys. 2004, 120 (1), 175–185. 10.1063/1.1630018. [DOI] [PubMed] [Google Scholar]
- Sears J. S.; Sherrill C. D.; Krylov A. I. A spin-complete version of the spin-flip approach to bond breaking: What is the impact of obtaining spin eigenfunctions?. J. Chem. Phys. 2003, 118 (20), 9084–9094. 10.1063/1.1568735. [DOI] [Google Scholar]
- Shao Y.; Head-Gordon M.; Krylov A. I. The spin–flip approach within time-dependent density functional theory: Theory and applications to diradicals. J. Chem. Phys. 2003, 118 (11), 4807–4818. 10.1063/1.1545679. [DOI] [Google Scholar]
- Slipchenko L. V.; Krylov A. I. Singlet-triplet gaps in diradicals by the spin-flip approach: A benchmark study. J. Chem. Phys. 2002, 117 (10), 4694–4708. 10.1063/1.1498819. [DOI] [Google Scholar]
- Slipchenko L. V.; Krylov A. I. Spin-conserving and spin-flipping equation-of-motion coupled-cluster method with triple excitations. J. Chem. Phys. 2005, 123 (8), 084107 10.1063/1.2006091. [DOI] [PubMed] [Google Scholar]
- Report of a Numerical Instability in the Parallel Version of the CC Code; Personal Communication Q-ChemSupport, 2022.
- Jiang Y.; Wang C.; Rogers C. R.; Kodaimati M. S.; Weiss E. A. Regio- and diastereoselective intermolecular [2 + 2] cycloadditions photocatalysed by quantum dots. Nat. Chem. 2019, 11 (11), 1034–1040. 10.1038/s41557-019-0344-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Y.; Weiss E. A. Colloidal Quantum Dots as Photocatalysts for Triplet Excited State Reactions of Organic Molecules. J. Am. Chem. Soc. 2020, 142 (36), 15219–15229. 10.1021/jacs.0c07421. [DOI] [PubMed] [Google Scholar]
- Prier C. K.; Rankic D. A.; MacMillan D. W. C. Visible Light Photoredox Catalysis with Transition Metal Complexes: Applications in Organic Synthesis. Chem. Rev. 2013, 113 (7), 5322–5363. 10.1021/cr300503r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El-Sayed M. A. Triplet state. Its radiative and nonradiative properties. Acc. Chem. Res. 1968, 1 (1), 8–16. 10.1021/ar50001a002. [DOI] [Google Scholar]
- Marian C. M. Spin–orbit coupling and intersystem crossing in molecules. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2 (2), 187–203. 10.1002/wcms.83. [DOI] [Google Scholar]
- Ortiz-Rodríguez L. A.; Crespo-Hernández C. E. Thionated organic compounds as emerging heavy-atom-free photodynamic therapy agents. Chem. Sci. 2020, 11 (41), 11113–11123. 10.1039/D0SC04747C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mills W. H.; Nixon I. G. CCCXXXII—Stereochemical influences on aromatic substitution. Substitution derivatives of 5-hydroxyhydrindene. J. Chem. Soc. 1930, 2510–2524. 10.1039/JR9300002510. [DOI] [Google Scholar]
- Maeda S.; Ohno K.; Morokuma K. An Automated and Systematic Transition Structure Explorer in Large Flexible Molecular Systems Based on Combined Global Reaction Route Mapping and Microiteration Methods. J. Chem. Theory Comput. 2009, 5 (10), 2734–2743. 10.1021/ct9003383. [DOI] [PubMed] [Google Scholar]
- Bashkatov A. N.; Genina E. A.; Kochubey V. I.; Tuchin V. V. Optical properties of human skin, subcutaneous and mucous tissues in the wavelength range from 400 to 2000 nm. J. Phys. D: Appl. Phys. 2005, 38 (15), 2543. 10.1088/0022-3727/38/15/004. [DOI] [Google Scholar]
- Wu S.; Butt H.-J. Near-Infrared-Sensitive Materials Based on Upconverting Nanoparticles. Adv. Mater. 2016, 28 (6), 1208–1226. 10.1002/adma.201502843. [DOI] [PubMed] [Google Scholar]
- Jelinkova H.Lasers for Medical Applications; Jelinkova H., Ed.; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Wenthold P. G.; Squires R. R. Biradical Thermochemistry from Collision-Induced Dissociation Threshold Energy Measurements. Absolute Heats of Formation of ortho-, meta-, and para-Benzyne. J. Am. Chem. Soc. 1994, 116 (14), 6401–6412. 10.1021/ja00093a047. [DOI] [PubMed] [Google Scholar]
- Hoffmann R. The Many Guises of Aromaticity. Am. Sci. 2015, 103 (1), 18. 10.1511/2015.112.18. [DOI] [Google Scholar]
- Schleyer P. v. R.; Maerker C.; Dransfeld A.; Jiao H.; van Eikema Hommes N. J. R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118 (26), 6317–6318. 10.1021/ja960582d. [DOI] [PubMed] [Google Scholar]
- Chen Z.; Wannere C. S.; Corminboeuf C.; Puchta R.; Schleyer P. v. R. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105 (10), 3842–3888. 10.1021/cr030088+. [DOI] [PubMed] [Google Scholar]
- Gershoni-Poranne R.; Stanger A.. NICS—Nucleus Independent Chemical Shift. In Aromaticity: Modern Computational Methods and Applications, 1st ed.; Fernandez I., Ed.; Elsevier: Cambridge, 2021. [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M. J.; Heyd J. J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Keith T. A.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.; et al. Gaussian 16, revision C.01; Gaussian Inc.: Wallingford, CT, 2016.
- Prall M.; Wittkopp A.; Schreiner P. R. Can Fulvenes Form from Enediynes? A Systematic High-Level Computational Study on Parent and Benzannelated Enediyne and Enyne–Allene Cyclizations. J. Phys. Chem. A 2001, 105 (40), 9265–9274. 10.1021/jp0028002. [DOI] [Google Scholar]
- Schreiner P. R.; Prall M. Myers–Saito versus C2–C6 (“Schmittel”) Cyclizations of Parent and Monocyclic Enyne–Allenes: Challenges to Chemistry and Computation. J. Am. Chem. Soc. 1999, 121 (37), 8615–8627. 10.1021/ja991282+. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.