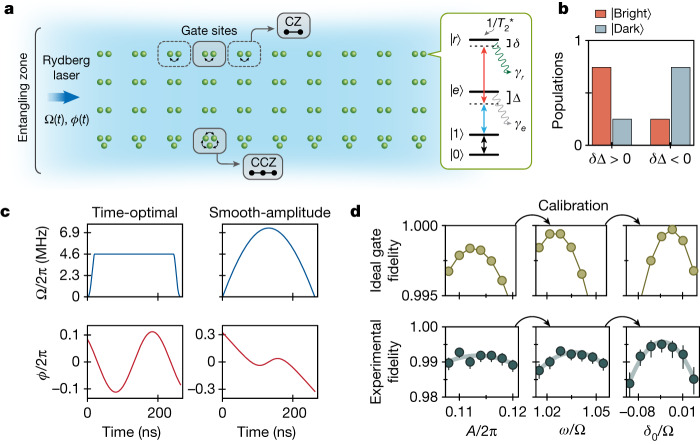
Fig. 1. Parallel implementation of high-fidelity entangling gates on a neutral-atom quantum computer.

a, Entangling gates are implemented by arranging atoms into designated gate sites in which they interact by means of Rydberg-blockade interactions when pulsing global Rydberg lasers. Two-qubit or three-qubit gates are performed by modulating the Rabi frequency Ω(t) and phase ϕ(t) profiles of the laser driving the first leg of the two-photon Rydberg excitation. Inset, atoms in the qubit state |1⟩ are excited to the Rydberg state |r⟩ through an intermediate excited state |e⟩, whereas atoms in |0⟩ are not excited. The main gate error sources include Rydberg-state decay γ_r, intermediate-state scattering γ_e and Rydberg dephasing $T_2^{*}$. b, Numerical comparison of average bright and dark state populations during the Rydberg gate. Choosing opposite intermediate-state (Δ) and two-photon (δ) detuning signs at the beginning of the gate maximizes population in the dark state, which minimizes the intermediate-state scattering error. c, Entangling gates are implemented with a single Rydberg laser pulse with smooth phase modulation ϕ(t), whose slope corresponds to a two-photon detuning δ(t). Several global parameters characterize the gate, allowing for a family of possible gate implementations, including a parameterized version of the time-optimal CZ gate⁸ and a smooth-amplitude CZ gate. d, Example gate calibration sequence. Tuning individual parameters of the parameterized time-optimal gate phase profile ϕ(t) = Acos(ωt − φ) + δ₀t allows for fast and simple global calibration (see Extended Data Fig. 5 for further experimental data). Error bars represent 68% confidence intervals.