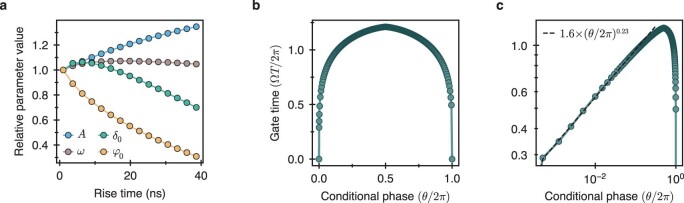
Extended Data Fig. 4. Robust and versatile two-qubit gates.

a, Robustness to experimental offsets. For some systematic experimental offsets, such as finite rise time of the 420-nm Rydberg laser pulse, an exact CZ gate can still be found. The relative values of gate parameters for the time-optimal gate are plotted as a function of pulse rise time. For no rise time, the parameter values used here are: A/2π = 0.0988, ω/Ω = 1.3629, φ₀ = −2.6082 and δ₀/Ω = −0.0187. b, Duration of a controlled-phase gate CPHASE(θ). The CZ gate (θ = π) is the longest in this gate family. Because faster gates are expected to have higher fidelity, an average CPHASE gate should perform even better than the CZ gate reported in this work, which is an exciting perspective for near-term digital simulation. c, Plotting on a log–log plot, we see that, for small angles θ, the gate time decreases with an approximate power law ΩT(θ)/2π = 1.6 × (θ/2π)^0.23. This suggests that applying very small phases can be costly and should be taken into account when designing digital simulation schemes. Although these small-angle gates are time-optimal when applying a single, fixed-amplitude pulse, different approaches could perform better. Exploring other exact and approximate gate schemes, such as Rydberg dressing and a detuned 2π pulse, in the small-angle regime is an interesting direction for future work.