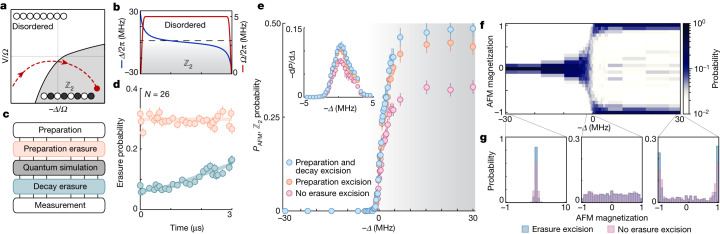
Fig. 3. Erasure conversion in quantum simulation.

a,b, We perform (b) quasi-adiabatic sweeps with N = 26 spins in the effective ground-state manifold of (a) an attractive Rydberg Hamiltonian (Methods), starting from the initially disordered phase and ending in the ${\mathbb{Z}}_2$ ordered phase. c, We perform two erasure images, one preceding the quantum simulation (to detect preparation errors) and one following (to partially detect Rydberg decay errors). d, The probability for detecting a preparation error (orange markers) remains constant while the probability for detecting a decay error (green markers) grows in agreement with the Rydberg lifetime and detection infidelities (solid lines; Methods). e, The total probability, P_AFM, for forming either of the AFM ${\mathbb{Z}}_2$ states is improved by performing erasure excision on all errors (blue markers), compared with only on preparation errors (orange markers) or performing no excision (pink markers). The sensitivity of P_AFM with respect to a change in Δ also increases with erasure excision (inset). f, The probability distribution for measuring a given AFM magnetization is initially peaked at 0 in the disordered phase, before bifurcating when entering the ${\mathbb{Z}}_2$ phase, consistent with spontaneous symmetry breaking. g, Deep in either phase, erasure excision leads to a sharpening of the probability distribution (left and right). Around the phase transition, we observe a close-to-flat distribution (middle). Error bars represent the standard error of the mean.