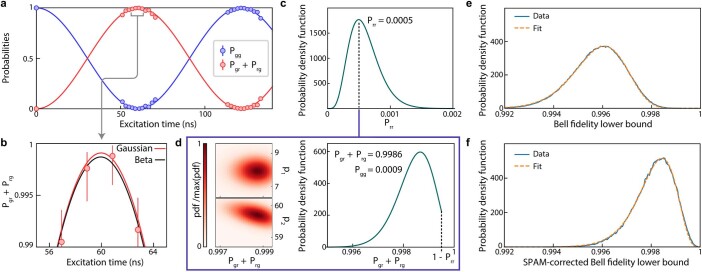
Extended Data Fig. 5. Bell state fidelity measurement from blockaded Rabi oscillations.

a, Probabilities of measuring both atoms in the ground state P_gg (blue markers) and a single atom in the ground state P_gr + P_rg (red markers) in the blockaded regime as a function of excitation time. Solid lines are guides to the eye. b, Zoom over the π time, where we prepare the Bell state $∣{\mathrm{\Psi }}^{+}⟩$ (see main text). We use a quadratic fit function of the form $f\left(x\right)=p_0+p_1{\left(x-p_2\right)}^2$ to extract the population values at π and 2π times. We show the fit results (i) assuming the experimental data have a Gaussian uncertainty (red line), and (ii) using their true Beta distribution (black line). c,d, Fitting method used to obtain the probability distributions of P_rr, P_gg, and P_gr + P_rg at π and 2π times. We first experimentally obtain the Beta distribution of the probability P_rr to observe both atoms in the Rydberg state. We then perform a joint fit on P_gr + P_rg and P_gg with the same p₁ and p₂ fit coefficients for both. We fix the value of P_rr, and condition the joint fit such that the sum of all probabilities is always equals to one. We repeat this process for various values of P_rr. The results shown here are for P_rr = 0.0005, which is the mode of the obtained Beta distribution for P_rr. The fitting method uses the true, experimentally measured Beta distribution of each data point. We obtain corresponding probability density functions for each P_rr. We perform this method independently for both π and 2π times. e, Resulting Bell state fidelity lower bound using the probability density functions of P_rr and P_gr + P_rg. We start by randomly drawing from the P_rr distribution, then assign the corresponding probability density function of P_gr + P_rg, and draw a value from it. The asymmetry between P_gr and P_rg is obtained by averaging over each experimental data point, and is assumed to be Gaussian. We repeat this process 1 million times for both π and 2π times. We obtain the corresponding probability density function (blue line), which we fit using a Beta distribution (orange dashed line). f, SPAM-corrected Bell state fidelity lower bound distribution, obtained by correcting the probabilities after randomly drawing them from their respective probability density functions.