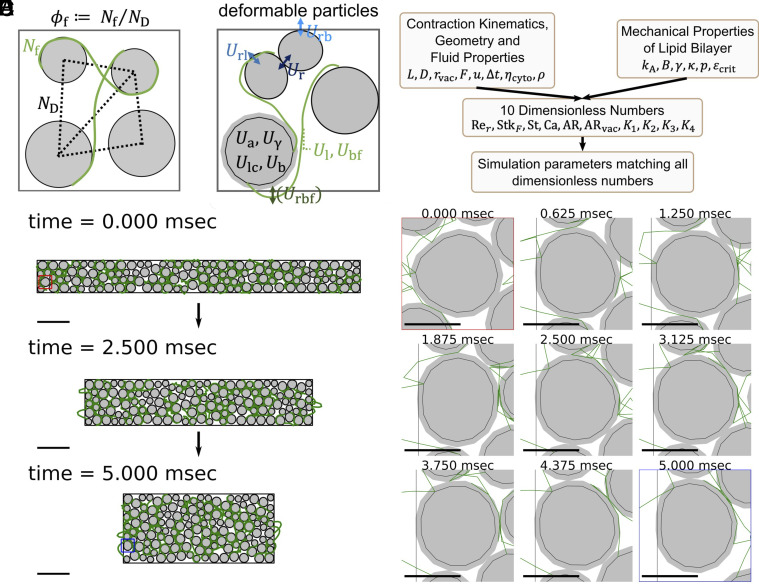
Fig. 3.

A 2D vertex-based entangled soft particle model allows us to study the effect of topological constraints on the mechanical properties of packed vacuoles in response to large shape changes. (A) We define filament fraction (${\varphi }_{\mathrm{f}}$) as the ratio between the number of strings ($N_{\text{f}}$) and the number of edges in the Delaunay diagram ($N_{\text{D}}$), which we use to describe the degree of topological constraints in the system. The volume fraction ($\varphi$) is defined as the ratio between the total area of particles and the area enclosed by the boundary. See SI Appendix, Section A.7.2. (B) We consider 10 energy terms in the model following the recommendation from Boromand et al. (33) with appropriate extensions to include the entangled strings. The system evolves according to an overdamped molecular dynamic scheme. See SI Appendix, Fig. S3. (C) We curated 10 dimensionless numbers from the known contraction kinematics, geometry, fluid properties, and mechanical properties of lipid bilayer membranes, and all simulation parameters are determined to match all 10 dimensionless numbers. The process ensures dynamic similarity and allows us to convert simulation results back to actual physical units and compare them with experiments. (D) Three snapshots of a simulated contraction process. The system displayed here has $\varphi =0.79$ and ${\varphi }_{\mathrm{f}}=0.268$. We report this particular simulation as it is the one which matches the experimental observation the best (Fig. 4). A constant boundary force is applied to deform the system during the contraction phase, with $\varphi$ kept constant. The red box marks one particle before contraction, while the blue box marks the same particle after contraction. The image sequence of the shape changes under this load for the sample particle is shown in (E) at a 625 $\mathrm{\mu }$s, or 0.625 ms time interval. Scale bar = 100 $\mathrm{\mu }$m in (D), while scale bar = 20 $\mathrm{\mu }$m in (E). Also see Movies S6 and S7.