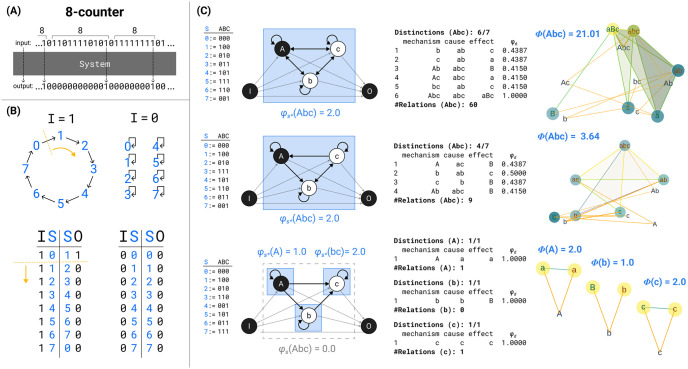
Fig 8. Functionally equivalent networks with different Φ-structures.
(A) The input–output function realized by three different systems (shown in (C)): a count of eight instances of input I = 1 leads to output O = 1. (B) The global state-transition diagram is also the same for the three systems: if I = 0, the systems will remain in their current global state, labeled as 0–7; if I = 1, the systems will move one state forward, cycling through their global states, and activate the output if S = 0. (C) Three systems constituted of three binary units but differing in how the units are connected and interact. As a consequence, the one-to-one mapping between the 3-bit binary states and the global state labels differ. However, all three systems initially transition from 000 to 100 to 010. Analyzed in state 100, the first system (top) turns out to be a single complex that specifies a Φ-structure with six distinctions and many relations, yielding a high value of Φ. The second system (middle) is also a complex, with the same φs value, but it specifies a Φ-structure with fewer distinctions and relations, yielding a lower value of Φ. Finally, the third system (bottom) is reducible (φs = 0) and splits into three smaller complexes (entities) with minimal Φ-structures and low Φ.