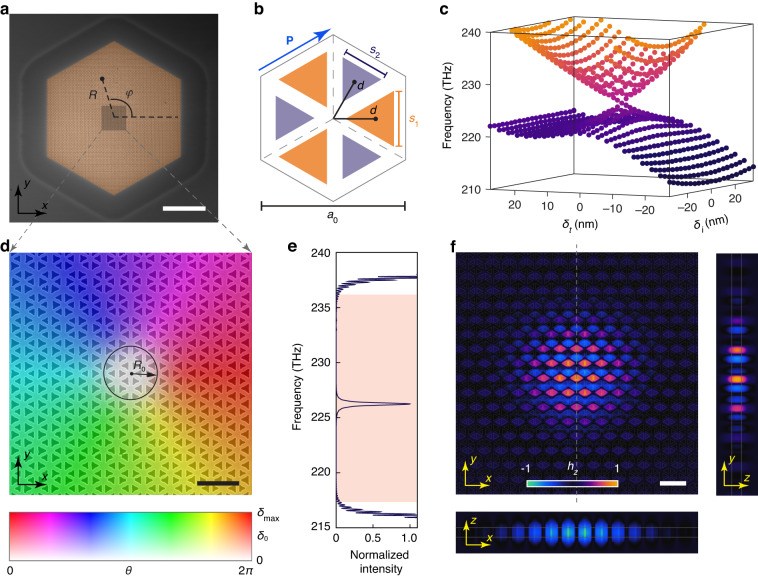
Fig. 2. Design and fabrication of the Dirac-vortex laser cavity.

a Scanning electron microscope image of the fabricated Dirac-vortex topological photonic crystal laser. R and φ are respectively the radial and angular coordinates of the real space. Scale bar, 10 µm. b Illustration of the detailed structure in a unit cell. The lattice constant of the hexagonal photonic crystal is a₀ = 641 nm. Each unit cell contains six triangular holes that can be classified into two groups (colored in purple and orange). The side lengths of the two groups of triangular holes are governed by parameters (s₁, s₂) = ($s_0+{\delta }_i$, $s_0-{\delta }_i$) with s₀ = 220 nm. The relative distance from the centers of these triangular holes to the center of the unit cell is d = a₀/3 − δ_t. Here, ${\delta }_i$ breaks the C₂ inversion symmetry and δ_t breaks the T_P translational symmetry along the vector P (marked by the blue arrow). c Simulated eigenfrequencies of the bulk states at the Γ point of the first Brillouin zone with different values of δ_i and δ_t. d Scanning electron microscope image of the photonic crystal structure near the vortex center. It is color-coded by the spatially varying parameters δ₀(R) = δ_max·[tanh(R/R₀)]⁴ and θ(φ) = φ, where R₀ defines the size of the region with a near-zero value of δ₀(R). Scale bar, 1 µm. e Simulated normalized intensity spectrum of the Dirac-vortex cavity. A topological Majorana bound state exists in the bulk bandgap (pink region). f Simulated modal profiles (h_z component) of the Majorana bound state. Scale bar, 1 µm