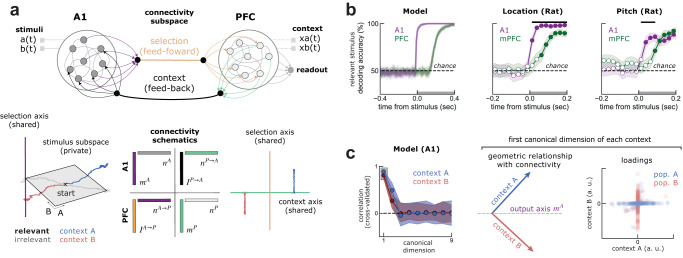
Fig. 5. Engineered multi-area model replicates A1 and PFC dynamics and produces predictions for across-area interactions.
a The interaction between A1 and PFC was set to occur through low-rank connectivity in opposite directions (feedforward in orange and feedback in gray). In contrast to the trained network, context is delivered transiently to PFC (dashed), stored in persistent activity and fed back to A1 (context, gray). In turn, stimuli are delivered to A1 and are not communicated to PFC, thus remaining in a “private subspace” of A1 (bottom left). The relevant stimulus, which is selected within A1 by integrating the stimuli and context, is communicated to PFC along the selection axis (selection, orange). Solid black circles represent the two variables that are shared across areas. On the bottom, connectivity schematics illustrates the geometric relationship between within- and across-area connectivity vectors, with similar colors illustrating strong overlap. b Relevant stimuli are encoded earlier in A1 than in PFC, as seen in the data for location (middle) and pitch (left). Full circles mark 25 ms bin with decoding significantly above chance (p < 0.05, one-sided bootstrap test; not corrected for multiple comparisons). Black bar marks time bins where A1 decoding is significantly above PFC decoding. Error-bars are SEM. c Estimation of the communication subspaces using canonical correlation analyses separately for each context (Communication subspace estimation in Methods). On the left, cross-validated correlation along different canonical dimensions is significant for two dimensions (bootstrapped mean and error bars are 95% C.I.). Highlighted in gray is the first canonical dimension of each context, used in the remaining panels. In the middle, we show that the first canonical dimensions of context A and B (left) are orthogonal, i.e. that A1 and PFC communicate through orthogonal subspaces in opposite contexts (red and blue, Methods), despite fixed connectivity. However, we show that these orthogonal subspaces are aligned along the output axis (mA, purple). On the right, we show that these orthogonal subspaces are supported by different populations. Neurons of population A have mostly null coefficients on the communication subspace during context B; conversely for neurons in population B.