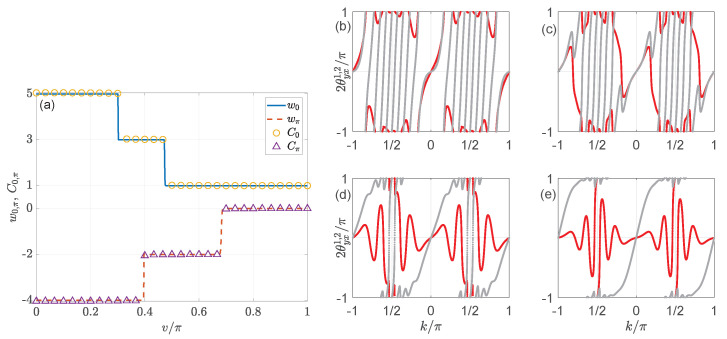
Figure 4.

Dynamical characterization of non-Hermitian Floquet topological phases [258]: (a) Winding numbers ($w_0$, $w_{\pi }$) and MCDs ($C_0$, $C_{\pi }$) versus the imaginary part of hopping amplitudes $J_1=u_1+iv$ and $J_2=u_2+iv$, with $(u_1,u_2)=(4.5\pi ,0.5\pi )$. The results for ($C_0$,$C_{\pi }$) are averaged over 50 driving periods. (b–e) Winding angles ${\theta }_{yx}^1$ (red dots) and ${\theta }_{yx}^2$ (gray dots) of the time-averaged spin textures versus the quasimomentum k, with $(u_1,u_2)=(4.5\pi ,0.5\pi )$. The imaginary parts of hopping amplitudes are $v_1=v_2=v$ with $v=0.2\pi$ for (b), $v=0.35\pi$ for (c), $v=0.6\pi$ for (d), and $v=0.9\pi$ for (e). The DWNs $({\nu }_1,{\nu }_2)$, derived from the winding angles around the first BZ are $(1,9)$ for (b), $(-1,7)$ for (c), $(-1,3)$ for (d) and $(1,1)$ for (e), yielding $(\frac{{\nu }_1+{\nu }_2}{2},\frac{{\nu }_1-{\nu }_2}{2})=(5,-4),(3,-4),(1,-2),(1,0)$ for (b–e), consistent with the $(w_0,w_{\pi })$ in (a) at the corresponding system parameters.