Prediction of brain age using structural magnetic resonance imaging: A comparison of accuracy and test–retest reliability of publicly available software packages

Abstract

Brain age prediction algorithms using structural magnetic resonance imaging (MRI) aim to assess the biological age of the human brain. The difference between a person's chronological age and the estimated brain age is thought to reflect deviations from a normal aging trajectory, indicating a slower or accelerated biological aging process. Several pre‐trained software packages for predicting brain age are publicly available. In this study, we perform a comparison of such packages with respect to (1) predictive accuracy, (2) test–retest reliability, and (3) the ability to track age progression over time. We evaluated the six brain age prediction packages: brainageR, DeepBrainNet, brainage, ENIGMA, pyment, and mccqrnn. The accuracy and test–retest reliability were assessed on MRI data from 372 healthy people aged between 18.4 and 86.2 years (mean 38.7 ± 17.5 years). All packages showed significant correlations between predicted brain age and chronological age (r = 0.66–0.97, p < 0.001), with pyment displaying the strongest correlation. The mean absolute error was between 3.56 (pyment) and 9.54 years (ENIGMA). brainageR, pyment, and mccqrnn were superior in terms of reliability (ICC values between 0.94–0.98), as well as predicting age progression over a longer time span. Of the six packages, pyment and brainageR consistently showed the highest accuracy and test–retest reliability.

Six software packages to predict brain age from structural MRI scans were evaluated. The brainageR and pyment packages showed the highest accuracy and reliability.

1. INTRODUCTION

Old age is the single strongest predictor for some of the most prevalent neurodegenerative disorders, such as Alzheimer's and Parkinson's disease (Hou et al., 2019; Niccoli & Partridge, 2012). By accurately assessing morphological changes in the aging brain, we can potentially identify relevant pathophysiological processes, monitor disease progression, and assess the effect of neuroprotective interventions (Higgins‐Chen et al., 2021).

1.1. Brain age prediction

Patterns of region‐specific changes in brain anatomy throughout the lifespan have been well‐described with in vivo magnetic resonance imaging (MRI; Bethlehem et al., 2022). Combined with the increasing availability of large MRI datasets, this has allowed for modeling the aging brain using machine learning techniques. Such models summarize different features of the aging brain into one single measure: the predicted age, or “brain age” (Franke et al., 2010), from T1‐weighted MR images. This estimate can then be used to calculate the predicted age deviation (PAD) for an individual:

$$\mathit{PA}{D}_i={\mathrm{Â}}_i-A_i$$ (1)

with  being the predicted age and A the chronological age. The PAD describes the divergence from the expected aging trajectory of a brain (Cole et al., 2017; Franke et al., 2010). A positive PAD indicates that a brain is biologically older than what would be expected from its chronological age, which in turn could translate into an increased risk of negative age‐related health outcomes. Over the past decade, several different MRI‐based brain age prediction models have shown that a high PAD is predictive of developing neurodegenerative disorders, cognitive decline, and overall mortality (Bashyam et al., 2020; Cole et al., 2018; Franke & Gaser, 2019; Han et al., 2021; Kaufmann et al., 2019).

1.2. Related reviews

The field of brain age estimation based on MRI is fast developing, and research groups are publicly sharing pre‐trained age prediction models that can be applied to new data without requiring any further training. These models range from classical regression, for example, ridge regression (Han et al., 2021) or Gaussian process regression (Cole et al., 2017), to gradient tree boosting (Kaufmann et al., 2019), and more complex deep learning estimators (Bashyam et al., 2020; Hahn et al., 2022; Jonsson et al., 2019; Leonardsen et al., 2022; Peng et al., 2021; Popescu et al., 2021). So far, a variety of studies compared different ML algorithms (More et al., 2023; Tanveer et al., 2023; Valizadeh et al., 2017) and different input features (i.e., region or voxel‐based; Baecker et al., 2021; Beheshti et al., 2022) to establish guidelines and best practices for the development of new brain age estimation models. However, an increasing number of publicly shared models trained on a large amount of data for immediate use on unseen data are published as well. To establish the usefulness of applying these models in, for example, clinical studies, a comprehensive review and analysis on independent, unseen data is necessary. Though some initial work has been done toward this aim (Bacas et al., 2023; Jirsaraie, Kaufmann, et al., 2023), no comprehensive comparison between the growing number of publicly shared, pre‐trained models has yet been published.

1.3. Objectives

Building on these previous results, we performed an extended literature search aiming to find all publicly available brain age prediction packages intended to be applied “off‐the‐shelf” on newly collected MRI data. Following this, we set out to perform a comprehensive comparison of these packages with regard to their accuracy, test–retest reliability, and ability to predict progressed age over a longer period of time. Such a comparison can provide an informative guide for future research that aims to implement brain age prediction software in clinical studies, for example, to monitor the progression of age‐related disease or to test the effect of interventions.

2. METHODS

2.1. Inclusion criteria

Software packages aiming to estimate the brain age from T1‐weighted MR images were included according to a set of criteria: (1) the package had to be publicly available; (2) the package had to include pre‐trained weights, allowing for direct application to an independent dataset; and (3) the required pipeline for any necessary preprocessing steps of MR images had to be publically available. The following packages were identified and evaluated: brainageR (Cole, 2019; Cole et al., 2017), DeepBrainNet (Bashyam et al., 2020), brainage (Kaufmann et al., 2019), ENIGMA (Han et al., 2021), pyment (Leonardsen et al., 2022), and mccqrnn (Hahn et al., 2022). A comparison of these packages is presented in Table 1, providing an overview of the applied machine learning algorithm, input features, demographics of the training data, and reported accuracy. A more detailed explanation of the literature search is given in the Supporting Information S1, where excluded packages are also listed. The package release and/or version used for the implemented packages in this study are listed in Table S1. Only software packages published prior to February 2023 were included.

TABLE 1.

Comparison of implemented software packages for brain age prediction.

Package	Algorithm	Features	Subjects	Age range, min–max (years)	Age distribution, mean (std) (years)	Reported accuracy
brainageR	GPR	Voxel based (segmented)	N = 3377	18–92	40.6 (21.4)	MAE = 4.9 years, r = .947
brainage	GTB	Region based	N = 35,474	3–89	–	r = .92/.93 (male/female)
DeepBrainNet	2D CNN	Voxel based (T1)	N = 11,729	3–95	–	MAE = 4.12 years
ENIGMA	RR	Region based	N = 2188	18–75	43.32 (15.42)/38.97 (15.68) (male/female)	MAE = 6.5/6.84 years, r = .854/.85 years (male/female)
pyment	SFCN	Voxel based (T1)	N = 53,542	3–95	–	MAE = 3.9 years, r = .975
mccqrnn	MCCQRNN	Voxel based (segmented)	N = 10,691	20–72	51.79 (11.37)	MAE = 2.94 years

Note: Algorithm: CNN, Convolutional Neural Network; GPR, Gaussian Process Regression; GTB, Gradient Tree Boosting; MCCQRNN, Monte Carlo dropout Composite Quantile Regression Neural Network; RR, Ridge Regression; SFCN, Simple Fully Convolutional Neural Network. Reported accuracy: MAE, Mean Absolute Error; r, Pearson's r between chronological and predicted age.

2.1.1. brainageR

The brainageR (https://github.com/james-cole/brainageR) software package is based on Gaussian process regression, which is a non‐parametric Bayesian regression approach. Briefly, the package takes raw T1‐weighted MR scans as input, utilizes SPM12 (https://www.fil.ion.ucl.ac.uk/spm/software/spm12/) for segmentation into gray matter, white matter, and CSF probability maps, and calculates spatially normalized parameters. Subsequently, these normalized probability maps are concatenated into one vector, and a principal component analysis is applied. The first 435 components are then used for predicting brain age with a Gaussian progress regression model. The brainageR package is implemented in R (https://www.r-project.org) and provides shell scripts for streamlined preprocessing and age prediction. The package was trained on 3377 healthy subjects with a mean age of 40.6 ± 21.4 years (mean ± standard deviation). The age of subjects was relatively evenly distributed between 18 and 92 years.

2.1.2. DeepBrainNet

The DeepBrainNet (https://github.com/vishnubashyam/DeepBrainNet) package uses a two‐dimensional convolutional network architecture built on top of a model trained on ImageNet, an all‐purpose image database used to pre‐train large deep learning models (Deng et al., 2009). The preprocessing is fully automated and implemented in the ANTs library (https://antsx.github.io/ANTsPyNet/docs/build/html/utilities.html). The preprocessing consists of n4 bias correction, skull‐stripping, and an affine registration to MNI space. Both the package and its implementation into the ANTs library are implemented in Python (https://www.python.org). We were not able to retrieve information on the age distribution of the training dataset.

2.1.3. brainage

The brainage (https://github.com/tobias-kaufmann/brainage) package is implemented in R and utilizes gradient tree boosting for age estimation. It uses measures of cortical thickness, area, and volume features for 180 regions of interest (ROIs) defined by the Glaser atlas (Glasser et al., 2016). FreeSurfer (Fischl, 2012) is used to parcellate these specified cortical regions. Additionally, standard summary statistics from the FreeSurfer recon‐all pipeline are used, resulting in a total of 1118 input features (i.e., 360 cortical thickness, 360 cortical area, 360 cortical volume, and 38 cerebellar–subcortical and cortical summary statistics). The training data (N = 35,474) approximately followed a bimodal age distribution, with a cluster in the range of ~3–35 years and the majority of subjects being in the older cluster in the range of ~ 45–80 years.

2.1.4. ENIGMA

The package provided by the ENIGMA group applies ridge regression to predict brain age based on FreeSurfer outputs, that is, subcortical volumes and cortical thickness, volume, and surface areas. The derived measures are averaged across hemispheres, resulting in a total of 77 features. The ENIGMA package provides separate models for males and females. It is available as a web application (https://photon-ai.com/enigma_brainage). The training data (N = 2188) approximately followed a bimodal age distribution with a majority of subjects in the younger cluster in the range of ~18–35 years and an older cluster in the range of ~35–75 years.

2.1.5. pyment

The pyment package (https://github.com/estenhl/pyment-public) is based on the “Simply Fully Convolutional Network” (Peng et al., 2021), which is a 3D convolutional neural network. The model predicts brain age based on skull‐stripped, MNI152 registered images. FreeSurfer is used for skull stripping, and FSL (Jenkinson et al., 2012) is used for reorientation and linear registration to MNI space. Pyment can be used at a command line interface, docker, or application programming interface. The training data (N = 53,542) approximately followed a bimodal age distribution, with a cluster in the range of ~3–35 years and the majority of subjects being in the older cluster in the range of ~ 45–80 years.

2.1.6. mccqrnn

The package mccqrnn (https://github.com/wwu-mmll/mccqrnn_docker) implements a Monte Carlo dropout composite quantile regression neural network that adjusts for uncertainty introduced by noise in the data and the model itself. The preprocessing uses the default segmentation pipelines from the SPM12 toolbox CAT12 (https://neuro-jena.github.io/cat/). The package takes the voxels of the gray‐matter segmentation as input. These are vectorized, standardized, and then used as input to the mccqrnn model. The model is implemented in Python and was trained, validated, and distributed via the PHOTON‐AI (https://photon-ai.com/) software. The package can be used via Docker or as a script. The package was trained on 10,691 subjects with a mean age of 51.79 ± 11.37 years. No additional information about the age distribution was available.

2.2. Neuroimaging datasets

2.2.1. Subjects and study design

In total, we used data from 372 healthy volunteers, of which a subset had participated in more than one MR examination (see Table 2 and Tables S2.1 and S2.2). All subject data were retrieved from the CIMBI database (Knudsen et al., 2016). All participants were “healthy controls” as defined by study‐specific criteria. Generally, a history or present state of neurological or psychiatric disorder was an exclusion criterion. All subjects also completed a psychical and neurological examination and a biochemical blood screening.

TABLE 2.

Description of included datasets.

Dataset	Subjects	Scans	Sex a M/F	Age a , Mean (SD) (years)	Age a , Min/max (years)	Elapsed time b , mean (SD) (years)	Elapsed time b , min/max (years)
CS	372	372	175/197	38.7 (17.5)	18.4/86.2	–	–
TrT	117	234	66/51	28.3 (9.5)	18.9/73.2	0.31 (0.24)	0.0/0.99
LT	47	105	34/13	32.3 (15.3)	19.9/79.7	2.11 (1.13)	1.01/6.83
Total	372	620	175/197	38.7 (17.5)	18.4/86.2	1.12 (1.37)	0.0/6.83

Abbreviation: CS, cross‐sectional; LT, longitudinal; TrT, test–retest.

^a Statistics for baseline scans.

^b Between baseline and follow‐up scans.

To compare (1) the accuracy, (2) test–retest reliability, and (3) the ability to track age progression over time for the brain age estimation packages, three datasets were derived from CIMBI: (1) 372 subjects between 18 and 86 years with at least one magnetization‐prepared rapid gradient‐echo high‐resolution (MPRAGE) T1‐weighted structural scan were identified. The first acquired, that is, baseline, T1‐weighted scans were used for a cross‐sectional analysis to evaluate the accuracy of the methods; (2) 117 subjects with a follow‐up scan within 1 year of the respective baseline were selected for a test–retest analysis to quantify the reliability of the methods; (3) 47 subjects with one or more follow‐up scans more than 1 year after their baseline scan were included for longitudinal analysis to compare age progression in chronological and biological age (Table 2).

A 1‐year time frame was selected as the cut‐off for the test–retest analysis in order to strike a balance between including an adequate number of scans and reducing the confound of actual brain aging over time. Given the rapid brain development experienced by individuals in their late teens and early adulthood (Mills et al., 2021), we also applied the same test–retest analysis to a subset of subjects with shorter intervals between scans, specifically fewer than 31 days, 14 days, and 1 day. Demographic information of these subsets is summarized in Table S3.1.

We also performed a sensitivity analysis restricted to subjects between 20 and 72 years, that is, including only data that lie within the age range of the original training data used for all packages (see Table 1). Demographic information for this subset is summarized in Table S4.2. Results from this sensitivity analysis are presented in Table S4.1.

2.2.2. MRI acquisition

T1‐weighted MRI scans were acquired on seven different scanners using standard parameters. Further information on MRI acquisition can be found in Knudsen et al. (2016). More information on the scanners and sequences used can be found in Tables S2.1 and S2.2.

2.2.3. Quality control

All scans passed a set of quality control measures. First, the tool MRIQC (Esteban et al., 2017) was used to provide summary reports for each raw T1 image. These reports provide quality measures, such as Dietrich's signal‐to‐noise ratio (Dietrich et al., 2007), and the entropy focus criterion as an indicator for blurring and motion (Atkinson et al., 1997). Such quality measures were compared for all scans using boxplots. If a scan was consistently outside 1.5 times the interquartile range, it was flagged as an outlier. Flagged outliers were manually inspected and discarded if the underlying data, or processing of data, was found to be corrupted. A similar procedure was performed for the FreeSurfer reconstruction, using QATools (https://surfer.nmr.mgh.harvard.edu/fswiki/QATools) and the ENIGMA protocol (https://enigma.ini.usc.edu/protocols/imaging-protocols/) for quality control. The quality control led to the exclusion of two MR images during the first stage (raw) and seven MR images during the second stage (FreeSurfer).

2.3. Statistical analysis

2.3.1. Age‐prediction accuracy

A cross‐sectional analysis was performed on the 372 baseline scans, using the mean absolute error (MAE),

$$\mathit{MAE}=\frac{1}{N}{\sum }_i^N\mid {\mathrm{Â}}_i-A_i\mid =\frac{1}{N}{\sum }_i^N\left|\mathit{PA}{D}_i\right|$$ (2)

as a measure of accuracy. The MAE reflects the average absolute difference between predicted age ${Â}_i$and chronological age $A_i$. For healthy controls, the MAE should, in theory, be close to zero since a healthy brain on a “normal” aging trajectory should reflect the chronological age of the individual.

Pearson's r was calculated to assess the correlation between predicted and chronological age, and between predicted age and PAD. If the evaluated brain age model predicts chronological age perfectly, then we would observe a Pearson's r = 1, whereas, in an unbiased model, Pearson's r for chronological age and PAD should be 0.

2.3.2. Test–retest reliability

Test–retest reliability was evaluated using the intraclass correlation coefficient (ICC) (Equation 3), specifically the ICC (1,1) (Weir, 2005), and the mean absolute difference (MAD) (Equation 4).

The ICC can be interpreted as the proportion of variance between subjects that is due to the true signal to the total signal (true + error) and can be seen as a metrics' ability to differentiate between subjects. A high ICC value (i.e., close to 1) means that the outcome measure can reliably rank subjects' brain age (or PAD) estimates, a prerequisite for doing correlation analyses. A low ICC (close to 0) means that the ranking is unreliable, and a correlational analysis using such an outcome would likely be uninformative. Specifically, ICC (1,1) is defined as follows:

$$\mathit{ICC}\left(1,1\right)=\frac{M{S}_B-M{S}_w}{M{S}_B+\left(k-1\right)·M{S}_W}$$ (3)

with $M{S}_B$ and $M{S}_W$ be the between and within subjects mean sum of squared variances, and $k$ the number of observations per subject. The ICC was calculated both for brain age predictions and the PAD values. Following recommendations from Portney and Watkins (2009), the reliability will be considered to be poor when ICC <0.5, moderate for 0.5–0.75, good for 0.75–0.9, and excellent for ICC values >0.9.

The MAD can be seen as an estimate of the error between baseline and follow‐up scan and should be close to zero, assuming there is no measurement error or change in age‐related biology. It is calculated as the absolute difference between two following brain age estimations:

$$\mathit{MAD}=\frac{1}{N}{\sum }_i^N\mid {\mathrm{Â}}_{2,i}-{\mathrm{Â}}_{1,i}\mid$$ (4)

To adjust for progressed chronological age between measurements, we introduce the age‐adjusted MAD

$$\mathit{\text{Adjusted}}\mathit{MAD}=\frac{1}{N}{\sum }_i^N\mid {\widehat{P}}_i-P_i\mid$$ (5)

as the MAD between progressed brain age (Equation 6) and progressed chronological age (Equation 7):

$${\widehat{P}}_i={\mathrm{Â}}_{2,i}-{\mathrm{Â}}_{1,i}$$ (6)

$$P_i=A_{2,i}-A_{1,i}$$ (7)

The subscripts 1 and 2 indicate baseline and follow‐up scan, respectively. Here, perfect reliability is indicated by a MAD and adjusted MAD = 0.

2.3.3. Tracking age progression over time

To assess the ability of different packages to track chronological age progression, we compared the adjusted MAD (Equation 5) for baseline and follow‐up scans that were acquired more than 1 year apart. If multiple follow‐up scans were available, the last follow‐up scan was used. Evaluating the adjusted MAD over a longer period allows us to investigate if progressed brain age (Equation 6) corresponds to actual progressed chronological age (Equation 7). A longitudinal adjusted MAD close to zero would therefore indicate that the respective package is able to accurately track chronological age over time.

To further assess the association between predicted age and chronological age, we used a linear mixed effects model, with predicted progressed biological age as the dependent variable, progressed chronological age as the independent variable, and subjects as a random effect (to account for the subset of subjects with more than two scans). A slope estimate close to 1 indicates that the progressed predicted age follows the actual progressed chronological age without any bias.

3. RESULTS

3.1. Age‐prediction accuracy

The results from the cross‐sectional analysis based on 372 baseline scans of healthy controls are summarized in Table 3 and Figure 1. The packages showed MAE values between 3.56 years (pyment) to 9.54 years (ENIGMA).

TABLE 3.

Results of cross‐sectional, test–retest, and longitudinal analysis.

	Cross‐sectional			Test–retest (<1 year)				Longitudinal (>1 year)
	MAE (years)	r	r, PAD	MAD (years)	Adj MAD (years)	ICC (95% CI)	ICC PAD (95% CI)	Adj MAD (years)	Beta (95% CI)
brainageR	4.04	0.96**	−0.13*	1.27	1.2	0.98 (0.98–0.99)	0.94 (0.92–0.96)	1.82	1.17 (0.68–1.67)
DeepBrainNet	6.13	0.89**	−0.43**	4.25	4.24	0.57 (0.44–0.68)	0.25 (0.08–0.41)	4.93	1.93 (0.8–3.05)
brainage	6.39	0.89**	−0.59**	2.32	2.35	0.94 (0.91–0.96)	0.91 (0.87–0.94)	2.88	0.65 (−0.47 to 1.77)
ENIGMA	9.54	0.66**	−0.59**	6.05	6.0	0.65 (0.53–0.74)	0.69 (0.58–0.77)	6.49	1.47 (−1.12 to 4.07)
pyment	3.56	0.97**	−0.31**	1.18	1.17	0.98 (0.98–0.99)	0.94 (0.91–0.96)	1.7	0.84 (0.44–1.24)
mccqrnn	4.46	0.95**	−0.46**	1.76	1.73	0.97 (0.96–0.98)	0.92 (0.89–0.94)	1.98	1.14 (0.60–1.67)

Note: Adj, adjusted; Beta, slope of linear mixed effects model fitted to assess the relation between progressed predicted age and progressed chronological age; r, Pearson's correlation coefficient, associated p‐value.

^* p < .01;

^** p < .005.

FIGURE 1.

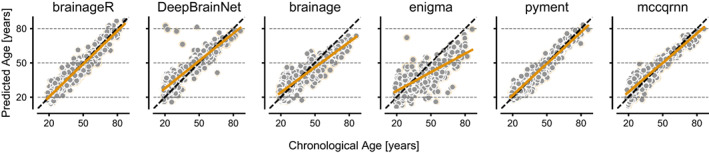
Predicted age versus chronological age of brainageR, DeepBrainNet, brainage, ENIGMA, pyment, and mccqrnn for age‐prediction on the cross‐sectional dataset based on 372 scans. The identity line is in dashed black, and the model regression line is in orange.

The correlation between age and predicted age ranged from r = .66 to r = .97 for the packages, with the strongest association shown for pyment and the weakest for ENIGMA. Packages also showed a large range for correlations between age and PAD, r = −.13 (brainageR) to r = −.59 (ENIGMA and DeepBrainNet; Table 3).

3.2. Test–retest reliability

Test–retest results based on 117 baseline/follow‐up scan pairs with less than a year elapsed between examinations are presented in Table 3. The MAD indicated that pyment (MAD = 1.18) produced the lowest deviation in estimated brain age between the two scans, while ENIGMA showed the highest deviation (MAD = 9.54). The adjusted MAD was slightly lower, but very close to the unadjusted MAD, indicating that little to no age‐related effects could be detected within the test–retest dataset.

The ICC showed excellent reliability for pyment, brainageR, and mccqrnn brain age predictions and PAD values, whereas DeepBrainNet and ENIGMA showed poor to moderate reliability (Table 3). For DeepBrainNet, the poor reliability was likely driven by some extreme PAD values, which can be identified in Figure 1. The ICC for PAD values followed a similar rank order as the ICC for brain age, but with consistently lower estimates (Table 3).

The sensitivity analysis on subsets with a shorter time between baseline and follow‐up scans showed similar results to the test–retest analysis using the 1‐year cutoff (Table 4). However, results from DeepBrainNet improved notably with a shorter test–retest interval, likely caused by the exclusion of subjects with outlying brain age prediction (visible in Figure 1).

TABLE 4.

Sensitivity test–retest analyses with shorter between‐scan intervals.

Method	MAD [years]				ICC (95% CI)
	<1 day	<14 days	<31 days	<365 days	<1 day	<14 days	<31 days	<365 days
brainageR	0.78	0.94	1.16	1.27	~1 (0.99–1.0)	0.99 (0.98–1.0)	0.99 (0.98–0.99)	0.98 (0.98–0.99)
DeepBrainNet	0.6	1.24	1.72	4.25	~1 (1.0–1.0)	0.98 (0.95–0.99)	0.97 (0.94–0.98)	0.57 (0.43–0.68)
brainage	1.68	2.05	1.93	2.32	0.98 (0.9–1.0)	0.95 (0.86–0.98)	0.96 (0.93–0.98)	0.94 (0.92–0.96)
ENIGMA	6.58	5.26	7.0	6.05	0.46 (−0.26 to 0 .86)	0.46 (−0.03 to 0 .78)	0.36 (0.05–0.61)	0.65 (0.53–0.74)
pyment	1.04	0.95	1.01	1.18	~1 (0.98–1.0)	0.99 (0.98–1.0)	0.99 (0.99–1.0)	0.98 (0.98–0.99)
mccqrnn	2.08	1.78	1.67	1.76	0.99 (0.93–1.0)	0.98 (0.96–0.99)	0.98 (0.97–0.99)	0.97 (0.96–0.98)

Note: MAD and ICC values are shown for the predicted brain age.

Abbreviations: ICC, intraclass correlation coefficient; MAD, mean absolute difference.

3.3. Tracking age progression over time

The ability of the different packages to predict age progression over time was assessed on 47 subjects using their baseline and last follow‐up scans (>1 year apart). The deviation between predicted brain age progression and chronological age progression over a longer period reflects the ability of the package to accurately model the structural changes of the brain over time. The results for each method are visualized in Figure 2a and summarized in Table 3. The adjusted MAD indicates that pyment, brainageR, and mccqrnn most closely tracked age progression. The full association between progressed predicted age and progressed chronological age is depicted in Figure 2b. This analysis included any additional MR scans that subjects had participated in between their baseline and latest follow‐up scan, resulting in a total of 105 scans. The slope of the fitted linear mixed effects model indicated a relationship close to 1 between predicted age progression and chronological age progression for mccqrnn, brainageR, and pyment (Table 3).

FIGURE 2.

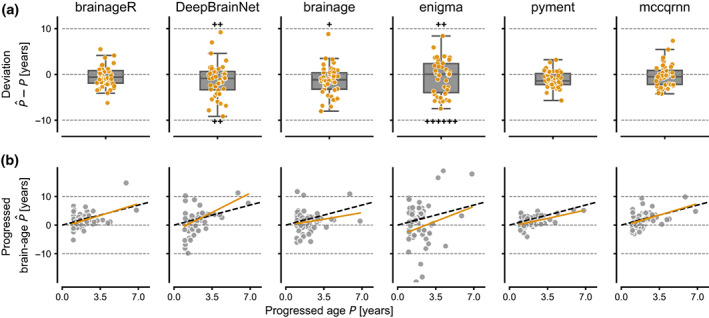
(a) Deviation between progressed brain age and the progressed chronological age for subjects with more than 1 year between MR scans. The boxplot represents the median and quartiles of the data, and the whiskers 1.5× the interquartile range. For visualization purposes, some outliers are not shown, but are instead represented by the plus‐sign to indicate their quantity and respective direction. (b) Association between chronological progressed age and progressed predicted age. The dashed black line represents the identity line, and the yellow line the fitted regression line from the LME.

4. DISCUSSION

The aim of this study was to compare the accuracy and reliability of publicly available software packages for brain age prediction. We identified and applied six software packages on three datasets retrieved from the CIMBI database (Table 2; Knudsen et al., 2016), data that were not used for training any of the evaluated algorithms. Out of the six software packages, pyment and brainageR showed superior performance in accuracy, test–retest reliability, and ability to predict progressed age over a longer period of time.

The observed high correlation with age and test–retest reliability results were in line with previous comparisons on other datasets (Bacas et al., 2023; Jirsaraie, Kaufmann, et al., 2023). For brainage, brainageR, and pyment, we were able to approximately reproduce the originally reported accuracies in terms of MAE and correlation between predicted age and chronological age (Cole et al., 2017; Kaufmann et al., 2019; Leonardsen et al., 2022). However, for the packages DeepBrainNet, Enigma, and mccqrnn, we found a larger deviation from previously reported outcomes (Bashyam et al., 2020; Hahn et al., 2022; Han et al., 2021).

The three CIMBI datasets used in this study came from several different 1.5T and 3T MR scanners and were acquired using different MPRAGE sequences (see Table S2). This heterogeneity could potentially be one reason for the discrepancy between previously reported values to those observed in this study. However, such heterogeneity can be viewed as a robustness check of the evaluated packages, as it represents real and common hardware/software heterogeneity of many existing MR datasets. As such, the results presented here have relevant construct validity with regard to the robustness of packages when confronted with such differences in data collection.

It is important to acknowledge that packages trained on an age distribution similar to the distribution of our independent test dataset could gain an advantage in our comparison. We did, however, not observe any clear pattern between age distribution in the training datasets, and the performance of our external validation set. For example, despite performing relatively poorly in our assessment, the ENIGMA package showed a similar focus on younger subjects in their training data and had a mean that was comparable to our validation dataset. Conversely, pyment, one of the top‐performing packages, had a training sample with a particular concentration in the older population, which differed from our sample. We also performed a sensitivity analysis on a subset of subjects with a more restricted age range (20–72 years old). This was done in order to assess if packages trained on such a restricted range (i.e., mccqrnn and ENIGMA) would display a better performance when training and validation data were more closely aligned. The results were however similar to the main analysis, and the rank‐order performance of the packages was preserved (Table S4.1).

The test–retest ICC values for pyment, mccqrnn, and brainageR were above 0.9 for predicted age and PAD estimates, indicating that these packages are excellent in differentiating between subjects. The ICC estimates for PAD were similar to those calculated on brain age, but consistently lower. This is to be expected, since the ICC depends on the error between scans, but also the between‐subject variance. Hence, the decreased reliability for PAD values were likely due to the differences in value ranges (e.g., for pyment, the predicted biological age range is 16.5–68.9 years, compared to −12.0 to 10.6 years for PAD values).

A high ICC has implications for future studies of association to, for example, clinical outcomes, since a reliable ranking of subjects (based on their predicted age or PAD) is a prerequisite for doing correlational analyses. The lower ICC value shown for DeepBrainNet PAD estimates suggests that a meaningful ranking of subjects is difficult to achieve with this package. Hence, an observed correlation between PAD values from this package and, for example, a clinical outcome would likely be attenuated compared to a true, underlying association. In addition, the better‐performing packages, brainageR and pyment, were able to reliably predict age progression over a longer time (>1 year). This is a pre‐requisite for the ability to detect an effect of slowed brain aging, for example, when running a clinical trial to evaluate a putative neuroprotective drug.

It is important to note that high accuracy in predicting chronological age (i.e., MAE close to zero) does not in itself mean that the outcomes have high validity. The point of a brain age prediction is to reflect the biological state of the brain, meaning that a high deviation from chronological age can contain important information about an accelerated, or slowed, biological aging process. In a healthy population like the one used in this study, it is reasonable to assume that the MAE should be low, but a package that shows a perfect correlation to chronological age (i.e., r = 1) is unlikely to reflect information on the biological state of the brain. In line with this, it has been suggested that more loosely fitting models might be better in distinguishing pathological brains from healthy ones (Bashyam et al., 2020). There is also growing evidence in the field suggesting that higher accuracy does not necessarily translate into improved utility in clinical settings (Jirsaraie, Gorelik, et al., 2023). To further assess the construct validity of the models, future studies should compare their ability to predict, for example, negative health outcomes.

Consistent with what has previously been reported for the six software packages (Bashyam et al., 2020; Cole et al., 2017; Hahn et al., 2022; Han et al., 2021; Kaufmann et al., 2019; Leonardsen et al., 2022), we found a negative correlation between PAD and chronological age (Table 3). Such an association is a well‐known phenomenon in MR brain age prediction software packages, and is hypothesized to be caused by regression to the mean age of the training population (Butler et al., 2021). This effect was stronger in ENIGMA, mccqrnn, and brainage, compared with pyment and brainageR. A dependency of the PAD on chronological age is a potential confounder when using brain age prediction. In order to negate such effect, it has been recommended to control for chronological age when using PAD estimates to, for example, differentiate between patient groups or predict clinical outcomes (Butler et al., 2021).

Our study is not without limitations. First, the MR images used for the test–retest and longitudinal analysis were mainly collected from a sample of younger subjects. Hence, our data are less suited to draw firm conclusions on the relative performance of packages' ability to reliably predict brain age in an older population. Second, the cutoff at 1 year to divide between test–retest and the longitudinal subset was arbitrarily chosen as a compromise between including a large enough N for both analyses, but avoiding any strong biological effects of aging in the test–retest analysis. A set of sensitivity analyses only including scans acquired within a shorter time frame (<1 month, <2 week as well as <1 day) showed similar results to the full test–retest dataset for all packages, except DeepBrainNet that displayed improved performance (see Table S3).

In this study, all weights for the applied packages come from pre‐training on different datasets, and no re‐training was performed. Hence, no conclusion about the usability of specific machine learning algorithms is possible based on the results presented here. It was, however, not our intention to compare the advantages and disadvantages of different algorithms, but to evaluate the performance of already available packages to be used as “off the shelves” products on a new MRI dataset for brain age prediction.

5. CONCLUSION

We applied six different publicly available age prediction software packages (DeepBrainNet, brainage, brainageR, ENIGMA, pyment, and mccqrnn) to three brain MRI datasets and compared their accuracy in predicting chronological age, test–retest reliability, and ability to predict age progression over time. The packages pyment, brainageR, and mccqrnn showed the overall best performance, suggesting that they could be useful for monitoring age‐related brain biology in, for example, clinical studies. Future studies comparing the performance of these packages in predicting age‐related clinical outcomes should be done to shed further light on their clinical utility.

CONFLICT OF INTEREST STATEMENT

The authors declare no conflicts of interest.

Supporting information

DATA S1: Supporting Information.

DATA S2: Supporting Information.

Dörfel, R. P. , Arenas‐Gomez, J. M. , Fisher, P. M. , Ganz, M. , Knudsen, G. M. , Svensson, J. E. , & Plavén‐Sigray, P. (2023). Prediction of brain age using structural magnetic resonance imaging: A comparison of accuracy and test–retest reliability of publicly available software packages. Human Brain Mapping, 44(17), 6139–6148. 10.1002/hbm.26502

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available on request from the CIMBI database (http://www.cimbi.dk/db) and an appropriate data sharing agreement. The data are not publicly available due to privacy or ethical regulatory restrictions.