Significance
Although NMR and MRI are indispensable measurement techniques in modern science and medicine, they have a major problem: low sensitivity. Among the many techniques available, dynamic nuclear polarization using photoexcited triplet state (triplet-DNP) can improve the sensitivity of magnetic resonance under mild conditions, but it requires strict angular adjustment of single crystals to obtain practical sensitivity, which is too demanding. Here, we demonstrate the highest polarization in triplet-DNP of unoriented samples by a chemical approach of molecular design of polarizing agents. This study opens a different path to inexpensive and versatile high-sensitivity NMR and MRI by DNP of a wide variety of biological materials under mild conditions.
Keywords: dynamic nuclear polarization, photo-excited triplet, NMR, MRI, quantum chemical calculation
Abstract
Triplet dynamic nuclear polarization (triplet-DNP) is a technique that can obtain high nuclear polarization under moderate conditions. However, in order to obtain practically useful polarization, large single crystals doped with a polarizing agent must be strictly oriented with respect to the magnetic field to sharpen the electron spin resonance (ESR) spectra, which is a fatal problem that prevents its application to truly useful biomolecular targets. Instead of this conventional physical approach of controlling crystal orientation, here, we propose a chemical approach, i.e., molecular design of polarizing agents; pentacene molecules, the most typical triplet-DNP polarizing agent, are modified so as to make the triplet electron distribution wider and more isotropic without loss of the triplet polarization. The thiophene-modified pentacene exhibits a sharper and stronger ESR spectrum than the parent pentacene, and state-of-the-art quantum chemical calculations revealed that the direction of the spin polarization is altered by the modification with thiophene moieties and the size of D and E parameters are reduced from parent pentacene due to the partial delocalization of spin densities on the thiophene moieties. The triplet-DNP with the new polarizing agent successfully exceeds the previous highest 1H polarization of glassy materials by a factor of 5. This demonstrates the feasibility of a polarizing agent that can surpass pentacene, the best polarizing agent for more than 30 y since triplet-DNP was first reported, in the unoriented state. This work provides a pathway toward practically useful high nuclear polarization of various biomolecules by triplet-DNP.
NMR and MRI are powerful analytical techniques that provide useful information in the chemical and clinical fields, but poor polarization of nuclear spins limits their sensitivity and hinders their versatility. Dynamic nuclear polarization (DNP) is a groundbreaking technology that boosts the sensitivity of NMR and MRI by transferring the polarization of electron spins to nuclear spins (1–7). However, sufficiently high electron spin polarization in thermal equilibrium requires harsh conditions, such as high-field (~ 7 T) and cryogenic temperatures (~1 K), preventing a wide range of practical applications (8–12).
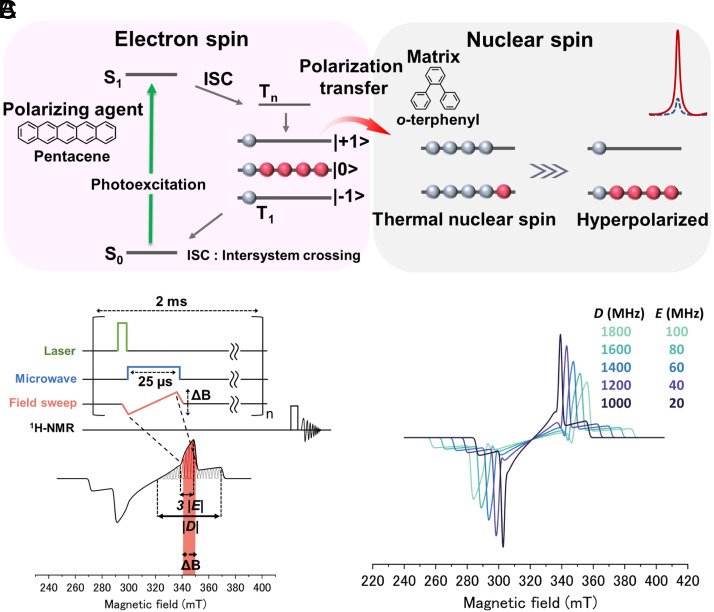
DNP using photoexcited triplet electrons (triplet-DNP) can achieve nuclear hyperpolarization even at room temperature since high electron spin polarization between triplet sublevels is achieved regardless of temperature by the spin-selective intersystem crossing (ISC) (Fig. 1A) (13–20). The polarization of triplet electron spins can be efficiently transferred to nuclear spins by integrated solid effect (ISE) sequence with microwave irradiation and magnetic field sweep (Fig. 1B). Spin polarization of triplet electron spins is transferred to nuclear spins in the ISE sequence by matching the Larmor frequency of electron spins in the rotating frame with that of nuclear spins in the laboratory frame. Since the electron spin resonance (ESR) linewidth of the triplet is broadened over 100 mT at X-band by hyperfine coupling and dipolar interactions between triplet electrons, only a limited part of spin packets simultaneously satisfies the resonance condition for polarization transfer. By sweeping the magnetic field during microwave irradiation, spin packets in the sweep range can be used for polarization transfer. However, the magnetic field sweep width is technically limited to about 10 mT since the field sweep must be slow enough to maintain the adiabatic condition within the lifetime of triplet polarization.
Fig. 1.
(A) Scheme of triplet-DNP. After photoexcitation of polarizing agents, spin-selective ISC produces spin-polarized triplet electrons. Triplet electron spin polarization is transferred to nuclear spin by the ISE. (B) ISE sequence. The pulsed laser excitation is followed by microwave irradiation and magnetic field sweep. (C) ESR simulation with various D and E values while other parameters are fixed (g = 2, B = 8.98 GHz, px = 0.4, py = 0.2, pz = 0.2).
In previous studies of triplet-DNP, the strategy has been to suppress the ESR linewidth broadening due to dipole interactions by strictly controlling the orientation of the single crystal doped with the polarizing agent relative to the magnetic field (16, 17, 21, 22). This strategy has enabled most of the electron spin packets to be utilized for polarization transfer, and nuclear spin polarization of several tens of percent has been achieved. However, this strategy is technically demanding because it requires growing large single crystals on the order of centimeters, and the orientation of the single crystals must be very strictly controlled. Furthermore, the matrix single crystals have been limited to aromatic compounds that can be doped with polarizing agents, which is a serious problem for application to important nonaromatic MRI probes such as pyruvate. Although the transfer of nuclear spin polarization to various molecules by dissolving hyperpolarized naphthalene single crystals at high concentrations has been reported, its medical applications are not easy because it has been limited to DNP in organic solvents (23). Considering these difficult challenges faced by the physical strategy of controlling crystal orientation, breakthroughs are needed to extend the application of triplet-DNP to a variety of biomolecules.
Here, we propose a solution to the essential problem of triplet-DNP by a chemical approach of molecular design of polarizing agents instead of a physical approach of orientation control. In order to achieve triplet-DNP of various biomolecules, it is necessary to achieve high nuclear polarization in randomly oriented samples, free from the constraints of single crystals. The key parameters are the zero-field splitting (ZFS) parameters D and E, which represent the energy gaps between triplet sublevels in the absence of magnetic field and determine the linewidth of the ESR spectrum of the triplet state (Fig. 1B) (24–26). Simulations with different values of D and E while keeping other parameters fixed show that the ESR spectrum becomes sharper as D and E become smaller in the examined range and that there are more spin packets within 10 mT, the magnetic field sweep width of the ISE sequence (Fig. 1C and SI Appendix, Fig. S4). D and E values are described as follows,
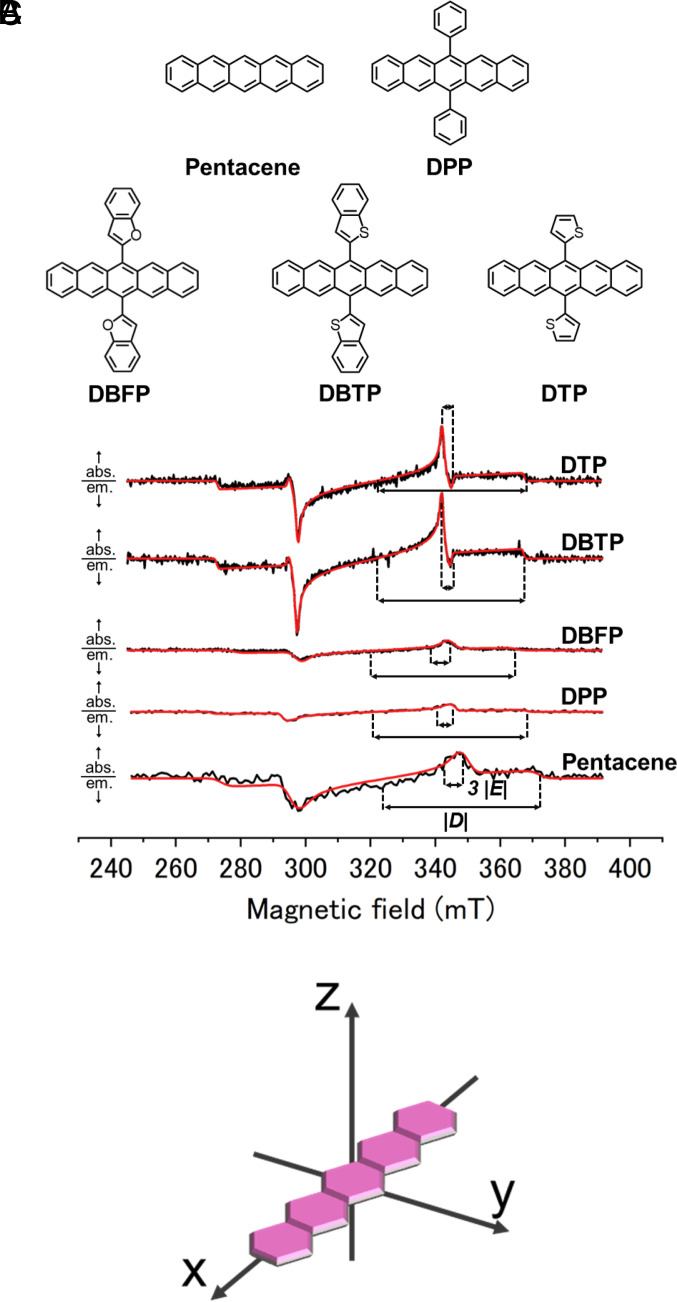
where r is the average distance between electron spins, x, y, z are dipole axes, ge is the g-factor, µB is the Bohr magneton, h is plank constant, and 0 is Magnetic permeability in vacuum. From the above equations, the D and E values are related to the average distance between spins and the rhombicity of the ZFS tensor, respectively. This implies that the molecular design with smaller D and E should make the triplet electron distribution more isotropic and symmetric, respectively. As a proof of concept, based on pentacene, the most typical polarizing agent of triplet-DNP, we designed unique polarizing agents by modifying pentacene with 5-membered rings, 6,13-di(benzofuran-2-yl)pentacene (DBFP), 6,13-bis(benzo[b]thiophen-2-yl)pentacene (DBTP), and 6,13-di(thiophen-2-yl)pentacene (DTP) (Fig. 2A). The relatively less sterically hindered furan and thiophene ring is not orthogonal to pentacene and expected to extend the conjugation, contributing to an extended and more symmetric triplet electron distribution. These polarizing agents actually exhibit a sharper and stronger ESR signal than pentacene, as well as a higher polarization ratio. The state-of-the-art quantum chemical calculations were performed to predict the ZFS parameters and the ISC rate. The calculations of the D tensor based on molecular structures allow us to predict the direction of the principal axis, i.e., the sign of the D and E parameters. It was confirmed that the modifications to parent pentacene enhance broadening the triplet electron distribution, providing theoretical support for the rationality of the present design guidelines, i.e., reducing the size of D and E values. Interestingly, the spin selectivity during the ISC, which is found to be governed by the vibronic effects, was proved to be altered by the modification with thiophene moieties. Triplet-DNP with novel polarizing agents exceeded the 1H polarization obtained so far in amorphous matrices by a factor of 5, demonstrating that they rationally outperform pentacene, which has been the best performance to date.
Fig. 2.
(A) Chemical structures of polarizing agents, pentacene, 6,13-diphenylpentacene (DPP), 6,13-di(benzofuran-2-yl)pentacene (DBFP), 6,13-bis(benzo[b]thiophen-2-yl)pentacene (DBTP) and 6,13-di(thiophen-2-yl)pentacene (DTP). (B) Time-resolve ESR spectra of pentacene, DPP, DBFP, DBTP, and DTP doped in β-estradiol at room temperature. Microwave frequencies for each spectral measurement are 8.988, 8.959, 8.983, 8.960 and 8.963 GHz, respectively. Results simulated with EasySpin toolbox in Mathlab are shown as red lines. (C) Principal axes of ZFS interaction of pentacene triplet electrons.
Results and Discussion
Time-Resolved ESR Measurements.
The polarizing agents DBFP, DBTP, and DTP were synthesized following the reported method (27), and their purity was confirmed by NMR and elemental analysis (see SI Appendix for details). For time-resolved ESR measurements, the polarizing agents were dispersed in β-estradiol glass. β-estradiol forms a colorless glass that is stable at room temperature, making it a convenient matrix for ESR measurements (28). Parent pentacene and phenyl-modified pentacene, 6,13-diphenylpentacene (DPP) were used in addition to DBFP, DBTP, and DTP for comparison (Fig. 2A).
Each polarizing agent was mixed with β-estradiol at a concentration of 0.01 mol% and dispersed in β-estradiol by heating to 453 K, which is above the melting point of β-estradiol, followed by rapid cooling with liquid nitrogen. The molecularly dispersed state of polarizing agents in β-estradiol was confirmed by absorption and fluorescence spectra. The peak positions and shapes of the absorption spectra of each polarizing agent in the β-estradiol glass were similar to those in the chloroform solution and were completely different from those of the neat solid, which had a large redshift and broadening (SI Appendix, Fig. S1). When the absorption spectra were measured by changing the concentration of DBTP in the β-estradiol glass, the spectral shape changed above 0.1 mol%, while it was maintained below 0.01 mol% (SI Appendix, Fig. S2). Pentacene and its derivatives do not emit fluorescence due to efficient singlet fission when aggregated (29), but the fluorescence spectra in the β-estradiol glass of each polarizing agent were similar to those in chloroform (SI Appendix, Fig. S3). From these results, we confirmed that each polarizing agent was dispersed in β-estradiol glass without aggregation at the concentration of 0.01 mol%.
Under pulsed laser irradiation at 527 nm, ESR spectra and signal decays of each polarizing agents in β-estradiol glass were measured at X-band (0.24 to 0.40 T) and room temperature (Fig. 2B and SI Appendix, Fig. S5). Laser intensity was set to 1.46 mJ/pulse for pentacene, DBFP, DBTP, and DTP and 2.19 mJ/pulse for DPP. ESR spectra were simulated by EasySpin toolbox in Matlab (30) and obtained parameters were summarized in Table 1. The principal axes of ZFS interactions were the same as pentacene and all signs of D and E values were assumed to be D > 0 and E < 0 (Fig. 2C) (31, 32). Compared to pentacene, DBTP and DTP exhibited much stronger and sharper ESR spectra, which is reflected in their smaller values of |D| and |E|. On the other hand, DPP showed similar ESR spectral shape and intensity and similar values of |D| and |E| as pentacene. The |D| value of DBFP was sufficiently smaller than that of DBTP, although there were some errors in the fitting parameters since the ESR intensity of DBFP was not clear enough (SI Appendix, Fig. S5). The reason for these differences in ZFS parameters will be discussed later based on theoretical calculations. The ESR intensity of DBFP was smaller than that of DBTP. This may be due to the lower ISC efficiency of DBFP in addition to the smaller population difference (Table 1 and SI Appendix, Table S1). Interestingly, pentacene, DPP, and DBFP were polarized along the x-axis, whereas DBTP and DTP were y-polarized, indicating a clear substituent effect. Decays of the ESR signal showed that both DBTP and DTP exhibited spin-lattice relaxation times T1e comparable to that of pentacene and long enough to apply the ISE sequence (SI Appendix, Fig. S6 and Table S2).
Table 1.
|D| and |E| values and relative population ratio of px, py, pz of each polarizing agent in the zero-field spin state
| |D| (MHz)* | |E| (MHz)* | px | py | pz | |
|---|---|---|---|---|---|
| Pentacene | 1,360.1 | 47.2 | 0.56 | 0.31 | 0.13 |
| DPP | 1,368.3 | 39.9 | 0.54 | 0.34 | 0.12 |
| DBFP | 1,190.9 | 45.1 | 0.60 | 0.26 | 0.14 |
| DBTP | 1,330.0 | 26.9 | 0.20 | 0.80 | 0.00 |
| DTP | 1,311.5 | 29.2 | 0.20 | 0.78 | 0.02 |
*Sign of D and E value are assumed to be D > 0 and E < 0.
Calculations of Spin-Selective ISC Rates.
To elucidate a detailed mechanism of the spin polarization experimentally observed for the pentacene derivatives, we performed quantum chemical calculations. It was assumed that the spin polarization is caused by a spin-selective ISC between the lowest singlet excited state (S1) and an energetically close triplet state (Tn) of the molecules. To characterize the final state of the ISC, energy levels of the low-lying triplet states of an unmodified pentacene molecule were calculated using the time-dependent density functional theory (TD-DFT) at the LC-BLYP/def2-TZVP level (33, 34). The range-separation parameter of the functional was set to 0.15. The 0-0 energy differences from S1 state were predicted as −1.33, −0.19, 0.77 eV for T1 (13B2u), T2 (13B1g), and T3 (13B3u) states of the pentacene, and therefore, the T2 state that is characterized by the highest occupied molecular orbital (HOMO) ➔ lowest unoccupied molecular orbital (LUMO)+1 and HOMO-1 ➔ LUMO singly excited state is likely to be the final state of the spin-selective ISC. The energy differences between the initial (S1) and final (T2) at each minimum were predicted to be −193, −85.1, and 3.96 meV for pentacene, DBTP, and DBFP molecules, respectively. The prediction that the energy level of T2 state is about the same or higher than that of S1 state for the DBFP molecule is consistent with the observation in our experiments that the fluorescence quantum yield of DBFP is higher than that of the other molecules, i.e., the ISC transition is not efficient in DBFP.
The ISC transition rate from the S1 to T2 spin sublevels , , and states are expressed approximately:
| [1] |
applying the Fermi’s Golden rule (FGR) where and indicate vibronic states associated, respectively, with and states, and are their energy levels, and is the spin-orbit coupling (SOC) operator. Since the potential energy surfaces of the spin sublevels are virtually degenerate, i.e., the energy differences are negligible in the prediction of the rates, the difference in the ISC rate for = should be caused solely by the difference in the magnitude of the SOC matrix elements (SOCMEs) . Because the SOCMEs of the planar coupling, caused by molecular vibrations that break the planar symmetry are dominant (35, 36), and the SOCMEs should be corrected by adding the first-order vibronic SOC term as:
| [2] |
where and denote the vibrational states in the initial ( ) and final ( ) electronic states. Hereafter, we denote the derivative at the reference structure (q = 0) as . There are many ways to evaluate Eq. 1. In this study, the time-dependent formulation (37–41) implemented in ORCA5 (42, 43) was used (41, 44), where the ISC rates are evaluated by the Fourier transform of the time-correlation function. The approximations adopted in the method, e.g., the potential surfaces are modeled by simple harmonic oscillators, can be insufficient to make quantitative predictions for the ISC rates but should be sufficient to predict the size relation between the spin sublevels. The calculated ISC rates in the pentacene, DBFP, and DBTP molecules are shown in Table 2. The most efficient ISC transitions were predicted for in the pentacene and DBFP molecules and for in the DBTP molecule. It is consistent with the spin polarization in T1 state observed in our ESR experiments.
Table 2.
Predicted ISC rates between S1 and T2 sublevels based on the Fermi Golden rule
| ns−1 | |||
|---|---|---|---|
| Pentacene |
(0.61) |
(0.38) |
(0.00) |
| DBFP |
(0.97) |
(0.02) |
(0.01) |
| DBTP |
(0.00) |
(0.89) |
(0.10) |
Relative rate ratios are shown in parentheses.
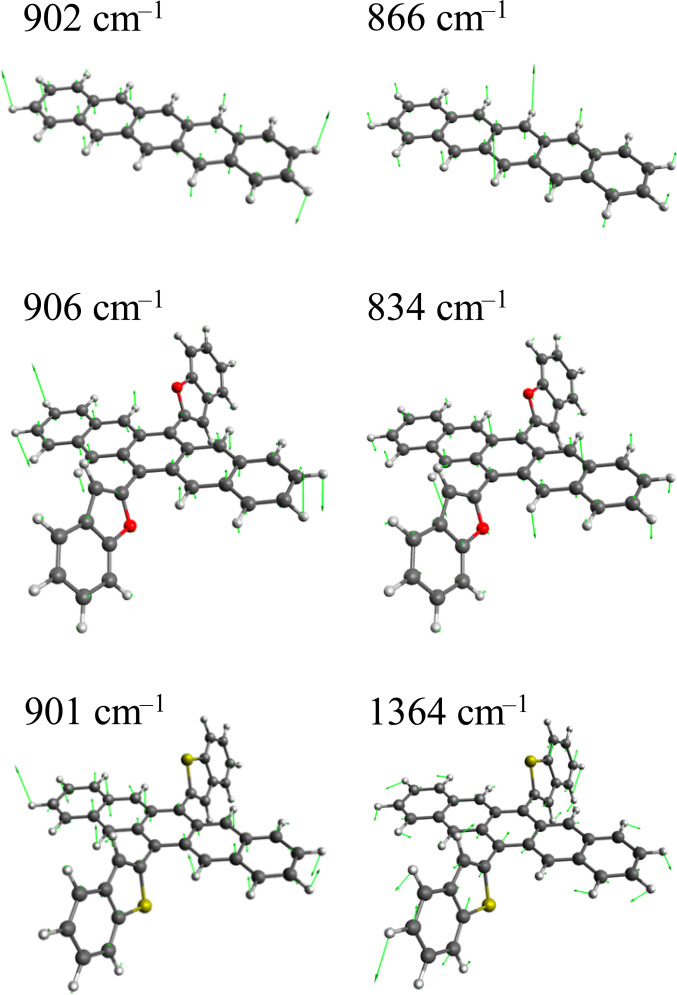
To analyse what vibrational modes contribute to enhancing the vibronic SOC, the first-order derivative of SOCME along each mode was calculated by finite difference techniques. The largest derivative of the SOCME of each sublevel is summarized in Table 3 and the associated normal modes are shown in Fig. 3. For the pentacene molecule, it was found that the out-of-plane modes consisting of C–H and C–C bending contribute to increasing the SOCME of the and components. Those out-of-plane distortions should mix the carbon π orbitals with σ bonding orbitals, i.e., the transition between carbon 2pz and 2py or 2px orbitals are involved in the ISC, and thus the SOCME of the and should be enhanced. None of the modes contribute to increasing that of the components. It implies that transitions between carbon 2px and 2py orbitals are negligible in the ISC even with the out-of-plane distortions. Similar observation was made for the DBFP molecule.
Table 3.
Derivatives of the SOCME along normal modes
| /cm−1 | /i cm−1 | /i cm−1 | /i cm−1 |
|---|---|---|---|
| Pentacene | |||
| 902 | 0.358 | 0.002 | 0.000 |
| 866 | 0.000 | 0.249 | 0.000 |
| 1,508 | 0.000 | 0.002 | 0.007 |
| DBFP | |||
| 906 | 0.249 | 0.004 | 0.005 |
| 834 | 0.009 | 0.127 | 0.002 |
| 1,579 | 0.042 | 0.003 | 0.029 |
| DBTP | |||
| 901 | 0.175 | 0.000 | 0.000 |
| 1,364* | 0.002 | 0.281 | 0.169 |
*The mode ( = 1,364 cm–1) provide the largest derivative for both Y and Z.
Normal modes that give the large derivatives are selected for each sublevel , , and .
Fig. 3.
Normalized displacement vector of the modes shown in Table 3. The modes along which the derivatives of the SOCME are less than 0.1, i.e., not significant, are omitted.
For the DBTP molecule, the largest derivatives were found along the modes involving displacements in the benzothiophene substituents, and those modes contribute only to and components. The derivative values along those modes are much larger than that along out-of-plane distortions of the pentacene backbone, which increase the SOCME of the and components. For the DBFP molecule, by contrast, the increase in the SOCME caused by the modes involving displacements of the benzofuran substituents is less than those by the out-of-plane modes of the pentacene backbone, and it results in that the transition to the component is the most efficient.
The discrepancy between the experimental and theoretical predictions of the order of and transition rates for the DBTP molecule, i.e., the transition rate to the was largely overestimated in the FGR calculations, should be attributed to the approximations adopted in the calculations. It is quite possible that the modes that significantly increase the SOCME of the are coupled with the rotation of the benzothiophene substituents and cannot be described by the harmonic oscillator model nor the first-order vibronic SOC model Eq. 2. In fact, the time-dependent method for the ISC rate could not converge in the case of DTP, which has similar structure to DBTP. In contrast, those approximations should work well for the pentacene molecule because all the modes that contribute to enhancing the ISC are out-of-plane modes and the transition should occur in the vicinity of the minimum along the modes for S1 and T2 states. In fact, the ratio is in good agreement with the experiment.
Calculations of ZFS Parameters.
To investigate the trends of D and E values observed in the experiments, nonrelativistic reference wavefunctions for the T1 state were obtained from the complete active space self-consistent field (CASSCF) calculations (45). Because the D and E values are parameters adopted in the phenomenological model Hamiltonian, there are many ways to define those values from the ab initio quantum chemical calculations. In the case of triplet states, it is straightforward to determine the D and E parameters such that energy gaps of the spin Hamiltonian reproduce the ab initio calculations. Because the contributions of the SOC term to the ZFS are negligible as compared with that of the spin-spin coupling (SSC) term for aromatic hydrocarbons, only the latter was considered in the calculations. The active space consisting of all the π orbitals of the pentacene backbones, i.e., as much as CAS(22e, 22o), were adopted in the CASSCF calculations. It exceeds the capability of the computer available for the foreseeable future, and the DMRG-CASSCF theory (46–48) implemented in the BLOCK2 program (49) was used with a sufficient bond dimension (m = 1,024) to circumvent the limitation. The D-tensor was calculated as the matrix elements of the SSC between the nonrelativistic triplet states with the different spin projections (50, 51), and the D and E parameters and the orientation of the principal magnetic axis were obtained by the diagonalization. The SSC two-electron integrals were evaluated by using the resolution of the identity (RI) approximation (32); the two- and three-center integrals were evaluated with Libcint and PySCF (52–54) package by using the translational invariance of the two-electron field gradient integrals.
Table 4 shows the calculated D and E parameters for the pentacene derivatives. One of the advantages of predicting the D-tensor by ab initio calculations is that the direction of the principal axes in the molecular axis system, i.e., sign of the D and E parameters, can also be directly determined. The signs were predicted to be D > 0 and E < 0, i.e., the energy ordering is > > . The signs of the parameters were identical to those reported by the previous experimental study for pentacene molecules in a p-terphenyl host crystal (55), while those have not been reported for the other molecules as far as we know. The signs predicted are necessary to reproduce the experimental ESR spectra which exhibit an EAE/AEA (E: emission, A: absorption) pattern for DBTP and DTP, and EEA/EAA pattern for Pentacene, DPP, and DBFP (Fig. 2B). The DBFP, DBTP, DTP, DPP, and pentacene molecules have larger D parameters in that order, which is in agreement with the experiments except for DPP of which |D| is larger by 8.2 MHz than pentacene in the experiment. It was found that the DBFP, which exhibits the smallest D value, has the smallest dihedral angle between the pentacene backbone and the substituents planes, and the spin density is more delocalized on the substituents than the DPP, DTP, and DBTP (SI Appendix, Fig. S16). Although the DPP, DTP, and DBTP have similar size of the dihedral angle, D value of the DTP and DBTP are clearly smaller than that of the DPP, which could reflect the effect of the M-shell electrons of sulfur atoms. Note that the electron SSC is a two-body interaction and it is not necessary explained solely by the one-electron property, spin density. In fact, it was reported that the mean-field approximation to the SSC causes a nonnegligible error for ZFS parameters (56).
Table 4.
Calculated D and E parameters obtained by the DMRG-CASSCF theory and dihedral angles between the pentacene backbones and the planar moieties
| D (MHz)* | E (MHz)* | Dihedral angle | |
|---|---|---|---|
| Pentacene | 1,171.4 | −44.5 | – |
| DPP | 1,143.1 | −28.7 | 69° |
| DBFP | 1,101.3 | −17.8 | 52° |
| DBTP | 1,129.0 | −21.1 | 71° |
| DTP | 1,125.2 | −19.9 | 69° |
*The signs D > 0 and E < 0 indicate that the energy ordering of the spin sublevels is > > where the molecular in-plane long and short axes and the out-of-plane axis correspond to the X, Y, Z principal axes.
As observed in the experiments, the |E| values for the pentacene derivatives were predicted to be very small as less than 50 MHz, though the size relationship between the molecules was not identical between the experiments and ab initio calculation. The energy gap between and sublevels is so small that there remains the possibility that the accuracy of the prediction is not fully converged within that range, e.g., the size of the active space and bond dimension, etc. Furthermore, the fitting made for experimental spectrum can involve errors when the signal is not enough clear.
The theoretical analysis indicates that molecular vibrations that break the planar symmetry and cause a mixing of carbon σ bonding orbitals with π orbitals determine the spin-selectivity in the ISC of the pentacene molecule. The spin-selectivity is largely changed by the substituent modifications; the substituent effect is so large that the direction of the polarization has altered between pentacene (long-axis) and DBTP (short-axis) molecules, though it seems that we should go beyond the harmonic oscillator model or the first-order vibronic SOC model for predicting the rate quantitatively for DBTP molecule. The ZFS parameters D and E are also changed by the modification with substituents. Because the spin-selectivity in the ISC and the ZFS parameters are determined by the SOC and SSC terms, respectively, those properties are expected to be controlled separately by substituent modifications.
Triplet-DNP Experiments.
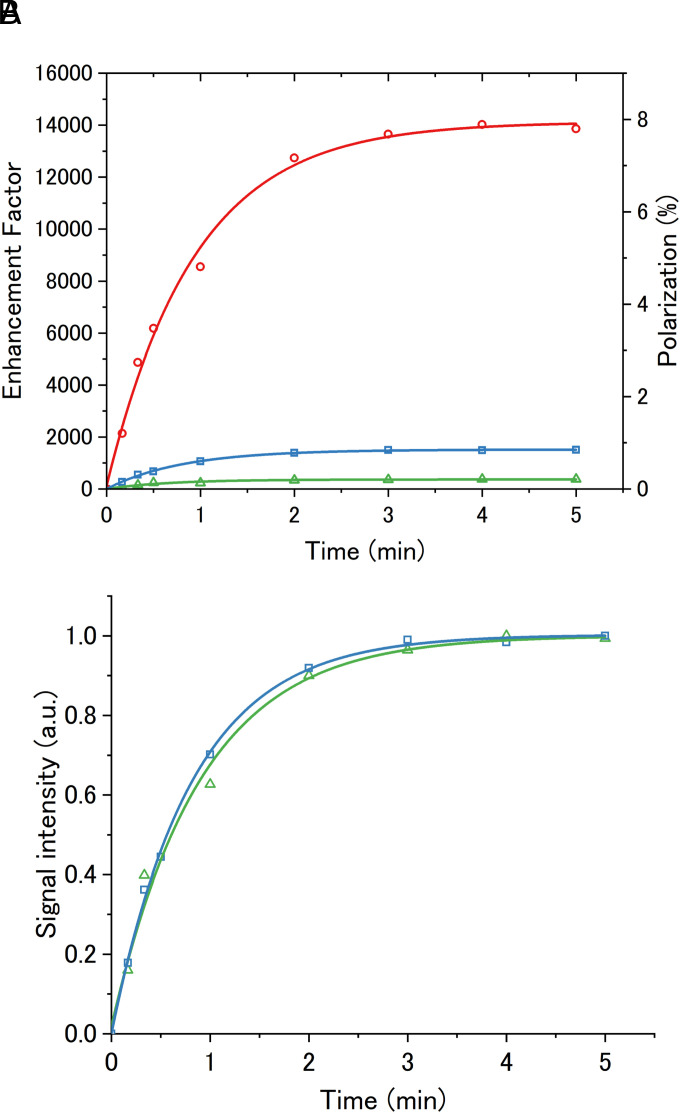
To evaluate the potential of the new polarizing agent, the 1H NMR signal intensity after triplet-DNP was compared between DTP and pentacene. Since β-estradiol has a short 1H spin-lattice relaxation time T1 of only a few seconds, o-terphenyl (OTP) was employed instead. OTP has been used as a model glass matrix for triplet-DNP because of its long T1 of about 60 s (SI Appendix, Fig. S9). The polarizing agents, DTP or pentacene, were doped in OTP using the same procedure except that the heating temperature was changed to 333 K. Triplet-DNP experiments were performed with OTP in the glassy state by ISE sequence under a magnetic field of 0.66 T for pentacene and 0.65 T for DTP at 120 K. After photoexcitation by irradiation of 527 nm pulsed laser, polarization was transferred from electron spins to nuclear spins by microwave irradiation (17.6 GHz) under magnetic field sweep (10 mT). After repeating this ISE sequence at a frequency of 500 Hz for a certain time, the sample was shuttled into an NMR coil within 1 s and 1H NMR spectra were measured. (see SI Appendix for details). The 1H polarization and enhancement factor was calculated by comparing the 1H NMR signal intensity of ethanol at 296 K and hyperpolarized signal after triplet-DNP at 120 K (SI Appendix, Fig. S10). Fig. 4A shows the buildup curves of 1H spin polarization by varying the time of triplet-DNP. Experimental parameters such as concentration of the polarizing agent and the magnetic field were optimized based on the intensity of the enhanced NMR signal (SI Appendix, Figs. S11 and S12). 1H polarization and enhancement factor of OTP after 5 min of triplet-DNP reached 0.85% and 1,540 times, respectively, with DTP, which was about four times larger than that with pentacene (0.21% and 370 times). The enhancement factor obtained by triplet-DNP also depends on other parameters of the polarizing agent, such as electron spin-lattice relaxation time T1e, triplet lifetime τT, fluorescence lifetime τFL, and triplet quantum yield ΦT but these parameters did not show significant differences for the examined polarizing agents (SI Appendix, Figs. S6–S8 and Tables S1 and S2). On the other hand, the buildup time constant Tb of DTP is was estimated to be 0.82 min when the buildup is fitted using the equation, A[1−exp(−t/Tb)], which is smaller than the Tb of pentacene (0.90 min) (Fig. 4B). This indicates that DTP shows the stronger and sharper ESR than pentacene and can generate more spin packets within the magnetic field sweep range. As a result, the accumulation rate of spin polarization increases, and the unique polarizing agent DTP gave significantly larger 1H polarization than the best-performing pentacene of the past. This was achieved by the rational molecular design of polarizing agents that simultaneously achieves spin–spin interaction control to reduce |D| and |E| values by making the triplet distribution more isotropic and symmetric, and SOC control with high sublevel selectivity in ISC.
Fig. 4.
(A) Build up curve of 1H signal intensity of OTP doped with pentacene (green line) and DTP (blue line), and partially deuterated OTP (OTP:[D14]OTP = 10:90 wt%) doped with DTP (red line). (B) Normalized build up curve of 1H signal intensity of OTP doped with pentacene (green line) and DTP (blue line).
Final polarization can be improved by reducing the density of 1H spins to increase the spin-lattice relaxation time T1 since the accumulation of polarization by triplet-DNP competes with the spin-lattice relaxation. By changing the glass matrix from OTP to a mixture of OTP and fully deuterated [D14]OTP (OTP:[D14]OTP: = 10:90 wt%), the 1H T1 value was elongated from 1 min to 3 min at 0.65 T and 120 K (SI Appendix, Fig. S9). Remarkably, this elongated T1 resulted in the further increase of 1H polarization and enhancement factor to 7.8% and 14,000 times, respectively (Fig. 4A), which is 5 times higher than the previous highest polarization of 1.5% in amorphous system by triplet-DNP (57).
Conclusions
In summary, we have proposed a rational design guideline for polarizing agent as a chemical approach to overcome the intrinsic problem of conventional triplet-DNP, which requires the use of big single crystals with strictly controlled orientation in order to obtain high polarization enhancement. Based on pentacene, the most representative polarizing agent of triplet-DNP, we have succeeded in reducing the ZFS parameters |D| and |E| while maintaining the high polarization of triplet by extending the conjugation through introducing the thiophene ring. This means that it is possible to simultaneously control the spin-spin interaction of the triplet that determines |D| and |E| and the SOC related to spin polarization. Theoretical calculations support for the rationality of the present design guidelines, i.e., by extending the π conjugation to make the distribution of spin density more isotropic and symmetric, the size of |D| and |E| values are reduced and the electron spin polarization is increased at the same time. The power of this chemical approach was demonstrated by exceeding by a factor of 5 the highest 1H polarization ever achieved by triplet-DNP in amorphous system. This indicates that a polarizing agent that exceeds the performance of pentacene, which has been considered the best over the last 30 y since triplet-DNP was first proposed, is feasible. We believe that further molecular design improvements based on the current discovery and development of equipment that allows a wider range of magnetic field sweeps, such as CHIRP pulses (58), and optimized excitation wavelength will lead to the practical application of triplet-DNP, achieving nuclear polarization of more than 10% for a wide variety of biomolecules under moderate conditions independent of molecular orientation.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
This work was partly supported by the JST-FOREST Program (JPMJFR201Y), JSPS KAKENHI (JP20H02713, JP22K19051, JP22J21293, and JP19H02675), The Murata Science Foundation, Research Foundation for Opto-Science and Technology, Kyushu University Platform of Inter-/Transdisciplinary Energy Research (Q-PIT) through its “Module-Research Program,” the RIKEN-Kyushu University of Science and Technology Hub Collaborative Research Program, and the RIKEN Cluster for Science, Technology and Innovation Hub (RCSTI).
Author contributions
Y.K. and N.Y. designed research; K.S., T.H., and K.M. performed research; K.T. and T.U. contributed new reagents/analytic tools; K.S. and K.M. analyzed data; and K.S., T.H., K.M., Y.K., and N.Y. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
Preprint Server: ChemRxiv, DOI: 10.26434/chemrxiv-2023-r18p7.
This article is a PNAS Direct Submission.
Contributor Information
Yuki Kurashige, Email: kura@kuchem.kyoto-u.ac.jp.
Nobuhiro Yanai, Email: yanai@mail.cstm.kyushu-u.ac.jp.
Data, Materials, and Software Availability
All study data are included in the article and/or SI Appendix.
Supporting Information
References
- 1.Carver T. R., Slichter C. P., Polarization of nuclear spins in metals. Phys. Rev. 92, 212–213 (1953). [Google Scholar]
- 2.Overhauser A. W., Polarization of nuclei in metals. Phys. Rev. 92, 411–415 (1953). [Google Scholar]
- 3.Hall D. A., et al. , Polarization-enhanced NMR spectroscopy of biomolecules in frozen solution. Science 276, 930–932 (1997). [DOI] [PubMed] [Google Scholar]
- 4.Franck J. M., Pavlova A., Scott J. A., Han S., Quantitative overhauser effect dynamic nuclear polarization for the analysis of local water dynamics. Prog. Nucl. Magn. Reson. Spectrosc. 74, 33–56 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ajoy A., et al. , Orientation-independent room temperature optical 13 C hyperpolarization in powdered diamond. Sci. Adv. 4, eaar5492 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dai D., et al. , Room-temperature dynamic nuclear polarization enhanced NMR spectroscopy of small biological molecules in water. Nat. Commun. 12, 6880 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Armstrong B. D., Han S., Overhauser dynamic nuclear polarization to study local water dynamics. J. Am. Chem. Soc. 131, 4641–4647 (2009). [DOI] [PubMed] [Google Scholar]
- 8.Ardenkjær-Larsen J. H., et al. , Increase in signal-to-noise ratio of > 10,000 times in liquid-state NMR. Proc. Natl. Acad. Sci. U.S.A. 100, 10158–10163 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jannin S., Dumez J.-N., Giraudeau P., Kurzbach D., Application and methodology of dissolution dynamic nuclear polarization in physical, chemical and biological contexts. J. Magn. Reson. 305, 41–50 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nelson S. J., et al. , Metabolic imaging of patients with prostate cancer using hyperpolarized [1- 13 C]pyruvate. Sci. Transl. Med. 5, 198ra108 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Golman K., in 't Zandt R., Thaning M., Real-time metabolic imaging. Proc. Natl. Acad. Sci. U.S.A. 103, 11270–11275 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen H. Y., Wilson C. B., Tycko R., Enhanced spatial resolution in magnetic resonance imaging by dynamic nuclear polarization at 5 K. Proc. Natl. Acad. Sci. U.S.A. 119, e2201644119 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Henstra A., Dirksen P., Wenckebach W., Th, Enhanced dynamic nuclear polarization by the integrated solid effect. Phys. Lett. A. 134, 134–136 (1988). [Google Scholar]
- 14.Henstra A., Lin T.-S., Schmidt J., Wenckebach W., Th, high dynamic nuclear polarization at room temperature. Chem. Phys. Lett. 165, 6–10 (1990). [Google Scholar]
- 15.Henstra A., Wenckebach W. T., Dynamic nuclear polarisation via the integrated solid effect I: Theory. Mol. Phys. 112, 1761–1772 (2014). [Google Scholar]
- 16.Iinuma M., et al. , Proton polarization with p-terphenyl crystal by integrated solid effect on photoexcited triplet state. J. Magn. Reson. 175, 235–241 (2005). [DOI] [PubMed] [Google Scholar]
- 17.Tateishi K., et al. , Room temperature hyperpolarization of nuclear spins in bulk. Proc. Natl. Acad. Sci. U.S.A. 111, 7527–7530 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nishimura K., et al. , Materials chemistry of triplet dynamic nuclear polarization. Chem. Commun. 56, 7217–7232 (2020). [DOI] [PubMed] [Google Scholar]
- 19.Takeda K., Triplet State Dynamic Nuclear Polarization (VDM Verlag, 2009). [Google Scholar]
- 20.Matsumoto N., et al. , Proton hyperpolarization relay from nanocrystals to liquid water. J. Am. Chem. Soc. 144, 18023–18029 (2022). [DOI] [PubMed] [Google Scholar]
- 21.Takeda K., Takegoshi K., Terao T., Dynamic nuclear polarization by electron spins in the photoexcited triplet state: II. High polarization of the residual protons in deuterated naphthalene. J. Phys. Soc. Jpn. 73, 2319–2322 (2004). [Google Scholar]
- 22.Negoro M., et al. , Dissolution dynamic nuclear polarization at room temperature using photoexcited triplet electrons. J. Phys. Chem. A. 122, 4294–4297 (2018). [DOI] [PubMed] [Google Scholar]
- 23.Eichhorn T. R., et al. , Hyperpolarized solution-state NMR spectroscopy with optically polarized crystals. J. Am. Chem. Soc. 144, 2511–2519 (2022). [DOI] [PubMed] [Google Scholar]
- 24.Yang T.-C., Sloop D. J., Weissman S. I., Lin T.-S., Zero-field magnetic resonance of the photo-excited triplet state of pentacene at room temperature. J. Chem. Phys. 113, 11194–11201 (2000). [Google Scholar]
- 25.Richert S., Tait C. E., Timmel C. R., Delocalisation of photoexcited triplet states probed by transient EPR and hyperfine spectroscopy. J. Magn. Reson. 280, 103–116 (2017). [DOI] [PubMed] [Google Scholar]
- 26.Hintze C., Steiner U. E., Drescher M., Photoexcited triplet state kinetics studied by electron paramagnetic resonance spectroscopy. ChemPhysChem 18, 6–16 (2017). [DOI] [PubMed] [Google Scholar]
- 27.Vets N., Smet M., Dehaen W., Reduction versus rearrangement of 6,13-Dihydro-6,13-Diarylpentacene-6,13-Diols affording 6,13- and 13,13’-substituted pentacene derivatives. ChemInform 36, 217–222 (2005). [Google Scholar]
- 28.Yamauchi A., et al. , Design guidelines to elongate spin-lattice relaxation times of porphyrins with large triplet electron polarization. J. Phys. Chem. A. 125, 4334–4340 (2021). [DOI] [PubMed] [Google Scholar]
- 29.Yost S. R., et al. , A transferable model for singlet-fission kinetics. Nat. Chem. 6, 492–497 (2014). [DOI] [PubMed] [Google Scholar]
- 30.Stoll S., Schweiger A., EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 178, 42–55 (2006). [DOI] [PubMed] [Google Scholar]
- 31.Loboda O., et al. , Ab initio calculations of zero-field splitting parameters in linear polyacenes. Chem. Phys. 286, 127–137 (2003). [Google Scholar]
- 32.Ganyushin D., Gilka N., Taylor P. R., Marian C. M., Neese F., The resolution of the identity approximation for calculations of spin-spin contribution to zero-field splitting parameters. J. Chem. Phys. 132, 144111 (2010). [DOI] [PubMed] [Google Scholar]
- 33.Tawada Y., Tsuneda T., Yanagisawa S., Yanai T., Hirao K., A long-range-corrected time-dependent density functional theory. J. Chem. Phys. 120, 8425–8433 (2004). [DOI] [PubMed] [Google Scholar]
- 34.Weigend F., Ahlrichs R., Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to RN: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 7, 3297 (2005). [DOI] [PubMed] [Google Scholar]
- 35.Henry B. R., Siebrand W., Spin-orbit coupling in aromatic hydrocarbons. Analysis of nonradiative transitions between singlet and triplet states in benzene and naphthalene. J. Chem. Phys. 54, 1072–1085 (1971). [Google Scholar]
- 36.Tatchen J., Gilka N., Marian C. M., Intersystem crossing driven by vibronic spin–orbit coupling: A case study on psoralen. Phys. Chem. Chem. Phys. 9, 5209 (2007). [DOI] [PubMed] [Google Scholar]
- 37.Borrelli R., Capobianco A., Peluso A., Generating function approach to the calculation of spectral band shapes of free-base chlorin including duschinsky and herzberg-teller effects. J. Phys. Chem. A 116, 9934–9940 (2012). [DOI] [PubMed] [Google Scholar]
- 38.Peng Q., Yi Y., Shuai Z., Shao J., Toward quantitative prediction of molecular fluorescence quantum efficiency: Role of Duschinsky rotation. J. Am. Chem. Soc. 129, 9333–9339 (2007). [DOI] [PubMed] [Google Scholar]
- 39.Niu Y., Peng Q., Deng C., Gao X., Shuai Z., Theory of excited state decays and optical spectra: Application to polyatomic molecules. J. Phys. Chem. A. 114, 7817–7831 (2010). [DOI] [PubMed] [Google Scholar]
- 40.Etinski M., Rai-Constapel V., Marian C. M., Time-dependent approach to spin-vibronic coupling: Implementation and assessment. J. Chem. Phys. 140, 114104 (2014). [DOI] [PubMed] [Google Scholar]
- 41.de Souza B., Neese F., Izsák R., On the theoretical prediction of fluorescence rates from first principles using the path integral approach. J. Chem. Phys. 148, 034104 (2018). [DOI] [PubMed] [Google Scholar]
- 42.Neese F., The ORCA program system. WIREs Comput. Mol. Sci. 2, 73–78 (2012). [Google Scholar]
- 43.Neese F., Wennmohs F., Becker U., Riplinger C., The ORCA quantum chemistry program package. J. Chem. Phys. 152, 224108 (2020). [DOI] [PubMed] [Google Scholar]
- 44.de Souza B., Farias G., Neese F., Izsák R., Predicting phosphorescence rates of light organic molecules using time-dependent density functional theory and the path integral approach to dynamics. J. Chem. Theory Comput. 15, 1896–1904 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Helgaker T., Jorgensen P., Olsen J., Molecular Electronic-Structure Theory (John Wiley & Sons, 2013). [Google Scholar]
- 46.Ghosh D., Hachmann J., Yanai T., Chan G. K.-L., Orbital optimization in the density matrix renormalization group, with applications to polyenes and β-Carotene. J. Chem. Phys. 128, 144117 (2008). [DOI] [PubMed] [Google Scholar]
- 47.Zgid D., Nooijen M., The density matrix renormalization group self-consistent field method: Orbital optimization with the density matrix renormalization group method in the active space. J. Chem. Phys. 128, 144116 (2008). [DOI] [PubMed] [Google Scholar]
- 48.Yanai T., Kurashige Y., Ghosh D., Chan G. K.-L., Accelerating convergence in iterative solution for large-scale complete active space self-consistent-field calculations. Int. J. Quantum Chem. 109, 2178–2190 (2009). [Google Scholar]
- 49.Zhai H., Chan G. K.-L., Low communication high performance ab initio density matrix renormalization group algorithms. J. Chem. Phys. 154, 224116 (2021). [DOI] [PubMed] [Google Scholar]
- 50.Harriman J. E., Theoretical Foundations of Electron Spin Resonance, Physical Chemistry, a Series of Monographs, vol. 37, (Academic Press, 1987). [Google Scholar]
- 51.Vahtras O., Loboda O., Minaev B., Ågren H., Ruud K., Ab initio calculations of zero-field splitting parameters. Chem. Phys. 279, 133–142 (2002). [Google Scholar]
- 52.Sun Q., et al. , The Python-based simulations of chemistry Framework (PySCF). WIREs Comput. Mol. Sci. 8, e1340 (2018). [Google Scholar]
- 53.Sun Q., et al. , Recent developments in the PySCF program package. J. Chem. Phys. 153, 024109 (2020). [DOI] [PubMed] [Google Scholar]
- 54.Sun Q., Libcint, An efficient general integral library for gaussian basis functions. J. Comput. Chem. 36, 1664–1671 (2015). [DOI] [PubMed] [Google Scholar]
- 55.Sloop D. J., Yu H., Lin T., Weissman S. I., Electron spin echoes of a photoexcited triplet: Pentacene in p-terphenyl crystals. J. Chem. Phys. 75, 3746–3757 (1981). [Google Scholar]
- 56.Sinnecker S., Neese F., Spin- spin contributions to the zero-field splitting tensor in organic triplets, carbenes and biradicals A density functional and Ab initio study. J. Phys. Chem. A. 110, 12267–12275 (2006). [DOI] [PubMed] [Google Scholar]
- 57.Tateish K., Negoro M., Kagawa A., Kitagawa M., Dynamic nuclear polarization with photoexcited triplet electrons in a glassy matrix. Angew. Chem. Int. Ed. 52, 13307–13310 (2013). [DOI] [PubMed] [Google Scholar]
- 58.Doll A., Jeschke G., Wideband frequency-swept excitation in pulsed EPR spectroscopy. J. Magn. Reson. 280, 46–62 (2017). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
All study data are included in the article and/or SI Appendix.