DNA language models are powerful predictors of genome-wide variant effects

Significance

Genetic variants across the genome contribute to complex human diseases and agricultural traits, but interpreting them can be challenging. We propose a genome-wide variant effect prediction approach based on unsupervised DNA language models, achieving state-of-the-art performance in Arabidopsis thaliana, a model organism for plant biology and a source of insight into human diseases. Our model, trained solely on DNA sequences, can be applied to any species with a reference genome, even in the absence of expensive functional genomics data. As the artificial intelligence field progresses, our approach can incorporate future advancements, offering a powerful and scalable tool to decipher the vast biological sequence diversity observed in nature.

Abstract

The expanding catalog of genome-wide association studies (GWAS) provides biological insights across a variety of species, but identifying the causal variants behind these associations remains a significant challenge. Experimental validation is both labor-intensive and costly, highlighting the need for accurate, scalable computational methods to predict the effects of genetic variants across the entire genome. Inspired by recent progress in natural language processing, unsupervised pretraining on large protein sequence databases has proven successful in extracting complex information related to proteins. These models showcase their ability to learn variant effects in coding regions using an unsupervised approach. Expanding on this idea, we here introduce the Genomic Pre-trained Network (GPN), a model designed to learn genome-wide variant effects through unsupervised pretraining on genomic DNA sequences. Our model also successfully learns gene structure and DNA motifs without any supervision. To demonstrate its utility, we train GPN on unaligned reference genomes of Arabidopsis thaliana and seven related species within the Brassicales order and evaluate its ability to predict the functional impact of genetic variants in A. thaliana by utilizing allele frequencies from the 1001 Genomes Project and a comprehensive database of GWAS. Notably, GPN outperforms predictors based on popular conservation scores such as phyloP and phastCons. Our predictions for A. thaliana can be visualized as sequence logos in the UCSC Genome Browser (https://genome.ucsc.edu/s/gbenegas/gpn-arabidopsis). We provide code (https://github.com/songlab-cal/gpn) to train GPN for any given species using its DNA sequence alone, enabling unsupervised prediction of variant effects across the entire genome.

The emergence of genome-wide association studies (GWAS) has significantly enhanced our ability to examine the genetic basis of complex traits and diseases in both humans and plants. In humans, GWAS have played a crucial role in identifying genetic variants associated with a range of traits, including schizophrenia and obesity (1). Similarly, in plants, GWAS have shed light on the genetic factors influencing traits such as drought tolerance, disease resistance, and yield (2). A central challenge in GWAS is pinpointing causal variants for a trait, as linkage disequilibrium (LD) can lead to spurious associations (3). This process, known as fine-mapping, serves as a foundation for constructing accurate, portable polygenic risk scores, and understanding the underlying biological mechanisms. Although experimental validation of causal variants is the gold standard, it is not scalable. Instead, a scalable fine-mapping strategy involves utilizing computational variant effect predictors (4), which vary from conservation scores to deep learning models trained on functional genomics data. Accurate variant effect prediction is also vital for diagnosing rare diseases and interpreting rare variants that lie beyond the scope of traditional GWAS (5).

Recently, state-of-the-art performance in predicting the effects of missense (coding) variants has been achieved by training unsupervised models on extensive protein sequence databases (6) or their corresponding multiple sequence alignments (7). These large language models can predict missense variant effects in an unsupervised manner, without the need for additional training on labeled data. This progress has been driven by advancements in natural language processing, where significant strides have been made by pretraining language models on vast text corpora. Pretrained models such as BERT can be fine-tuned for downstream tasks such as sentiment analysis (8). More recently, language models like GPT-4 have demonstrated impressive leaps in test performance across various disciplines, from law to computer science (9).

A widely used approach to interpreting noncoding variant effects involves training a supervised model to predict functional genomics data—such as chromatin accessibility, transcription factor binding, or gene expression—and then evaluating variants based on how they disrupt these predictions. This approach was first introduced by DeepSEA (10), which utilized 919 functional genomics tracks, and has since been refined by Enformer (11) with 6,956 tracks and Sei (12) with 21,907 tracks. However, this approach’s success depends on the availability of high-quality functional genomics data from a diverse array of cell types, which can be prohibitively expensive to generate for most species. Certain models focus on specific classes of noncoding variants. For instance, classifiers trained solely on sequence data can predict the impact of intron variants on splicing patterns (13, 14). To evaluate the effects of regulatory variants, Lee et al. (15) developed a support vector machine that distinguishes putative regulatory sequences from random genomic sequences. More recently, a deep learning model capable of predicting Hi-C signal from sequence data demonstrated its potential to predict the impact of regulatory variants on DNA folding within the nucleus (16). Additionally, a deep learning model (17) was successfully trained to predict DNA methylation levels of CpG sites from sequence data, enabling the prediction of noncoding variant effects on DNA methylation.

However, variant type-specific models may not be well suited for detecting trait-associated rare variants, fine-mapping, or calculating polygenic scores, as these tasks are facilitated by the comparison of genome-wide variants all together. For instance, a model that is exclusively designed for either missense or regulatory variants would not be able to prioritize between a de novo missense variant and a de novo promoter variant observed in an individual with a rare disease. An important class of genome-wide scores are conservation scores such as phyloP (18) and phastCons (19), which are computed from genome-wide alignment of multiple species. Since these do not require functional genomics data, they have been widely applied to many systems, including nonmodel organisms (20). In humans, CADD is another important genome-wide variant effect predictor that combines conservation and functional genomics annotations and is trained to distinguish between an inferred set of putative benign and putative pathogenic variants (21, 22).

In this paper, we introduce the GPN, a multispecies DNA language model trained using self-supervision. While existing DNA language models (23–29) have not yet demonstrated the ability to make accurate variant effect predictions based on self-supervision alone, GPN presents a unified approach capable of accurate unsupervised prediction of genome-wide variant effects. We demonstrate its utility by achieving state-of-the-art performance in Arabidopsis thaliana, a model organism for plant biology closely related to many agriculturally important species, as well as a source of insight into human diseases (30). Moreover, GPN outperforms genome-wide conservation scores such as phyloP and phastCons, which rely on whole-genome alignments of 18 closely related species (20). GPN’s internal representation of DNA sequences can distinguish genomic regions like introns, untranslated regions, and coding sequences. Additionally, the confidence of GPN’s predictions can help reveal regulatory grammar, such as transcription factor binding motifs. Our results lay the foundation for developing state-of-the-art genome-wide variant effect predictors for any species using genomic sequence alone, which can be readily integrated into GWAS fine-mapping and polygenic risk scores.

Results

Training a Multispecies DNA Language Model.

We used unaligned reference genomes from A. thaliana and seven related species within the Brassicales order to pretrain a language model based on a convolutional neural network (SI Appendix, Table S1). This model was designed to predict masked nucleotides conditioned on their local genomic context (Fig. 1 and Materials and Methods). During the training process, we encountered challenges with repetitive elements, which can be functionally significant but are heavily overrepresented in the genomes (31). We found that reducing the weight of prediction loss for repetitive regions led to lower test perplexity in nonrepetitive regions, which are often of greater interest (SI Appendix, Table S2). Compared to full down-weighting, moderate down-weighting results in a similar improvement in perplexity for nonrepetitive regions without sacrificing genome-wide perplexity as much. Consequently, we focus on this model throughout the remainder of the paper unless otherwise specified.

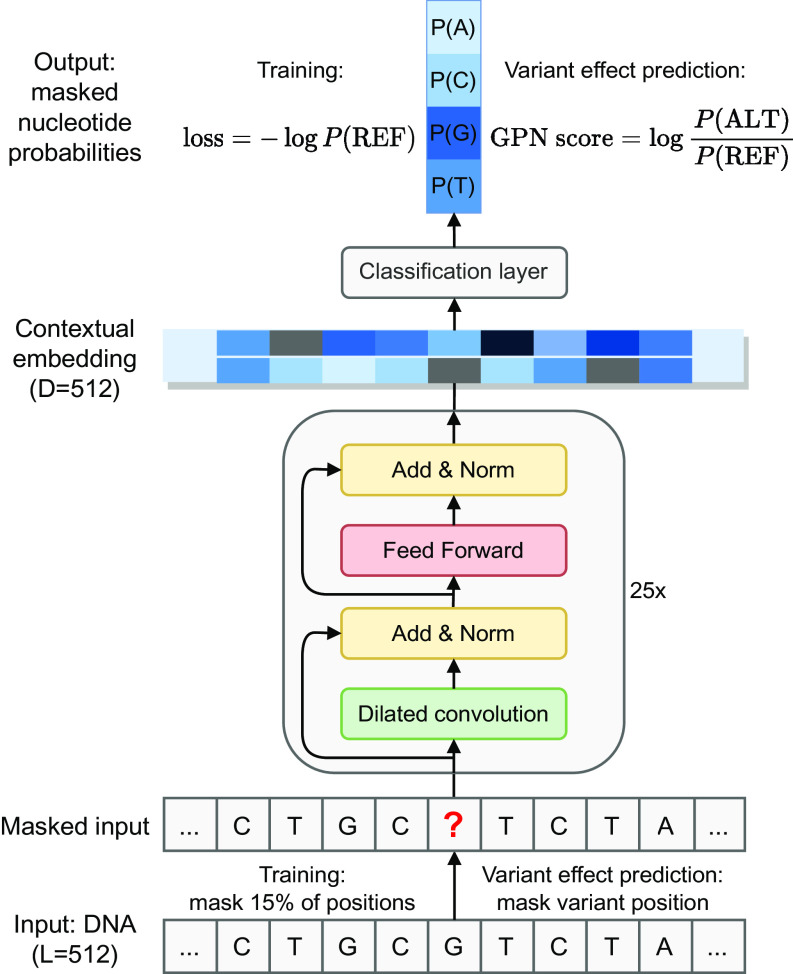
Fig. 1.

Overview of GPN. The input is a 512-bp DNA sequence where certain positions have been masked, and the goal is to predict the nucleotides at the masked positions. During training, 15% of the positions are masked. During variant effect prediction, only the variant position is masked. The sequence is processed through a convolutional neural network resulting in a high-dimensional contextual embedding of each position. Then, a final layer outputs four nucleotide probabilities at each masked position. The model is trained on the reference sequence with the cross-entropy loss. The GPN variant effect prediction score is defined as the log-likelihood ratio between the alternate and reference allele. L: window length in base pairs. D: embedding dimension. REF: reference allele. ALT: alternate allele.

Unsupervised Clustering of Genomic Regions.

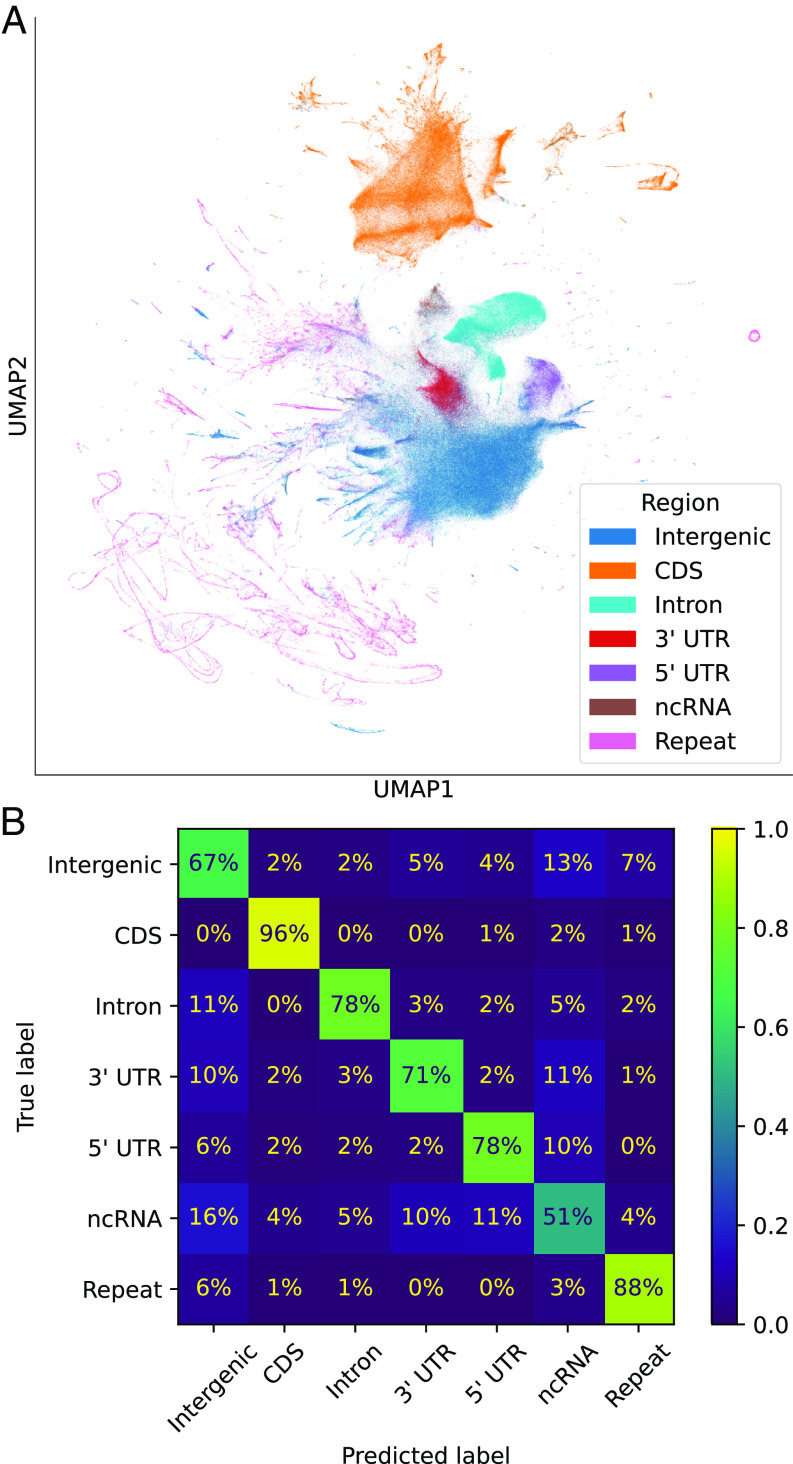
To understand how well the model has learned the structure of the genome, we averaged GPN’s contextual embeddings (512 dimensions) of nucleotides over 100 base pair (bp) windows from the reference genome and visualized them using UMAP (32) (Fig. 2A). Notably, GPN, trained without any supervision, has learned to distinguish genomic regions such as intergenic, introns, coding sequences (CDS), untranslated regions (UTR), and noncoding RNA (ncRNA). To quantify GPN’s ability to distinguish genomic regions, we trained a logistic regression classifier using the averaged embeddings as features, achieving the highest accuracy on CDS (96%) and the lowest on ncRNA (51%), the least frequent class. As summarized in Fig. 2B, the highest confusion was observed between intergenic regions and ncRNAs; this may be partly explained by errors in ncRNA annotation, which is especially challenging given their low expression levels and poor conservation (33). This level of classification accuracy cannot be achieved merely through $k$-mer frequencies ($k=3$: 8% to 70%; $k=6$: 15% to 67%; see SI Appendix, Fig. S1). We also note that, to some extent, GPN embeddings can distinguish different repeat families (SI Appendix, Fig. S2).

Fig. 2.

Unsupervised clustering of genomic windows. (A) UMAP visualization of GPN embeddings averaged over nonoverlapping 100-bp windows along the genome, annotated with gene region. (B) Confusion matrix for classification of gene regions using a logistic regression model trained on averaged embeddings. Each chromosome was predicted from a model trained on the remaining chromosomes.

DNA Motifs Revealed by High-Confidence Model Predictions.

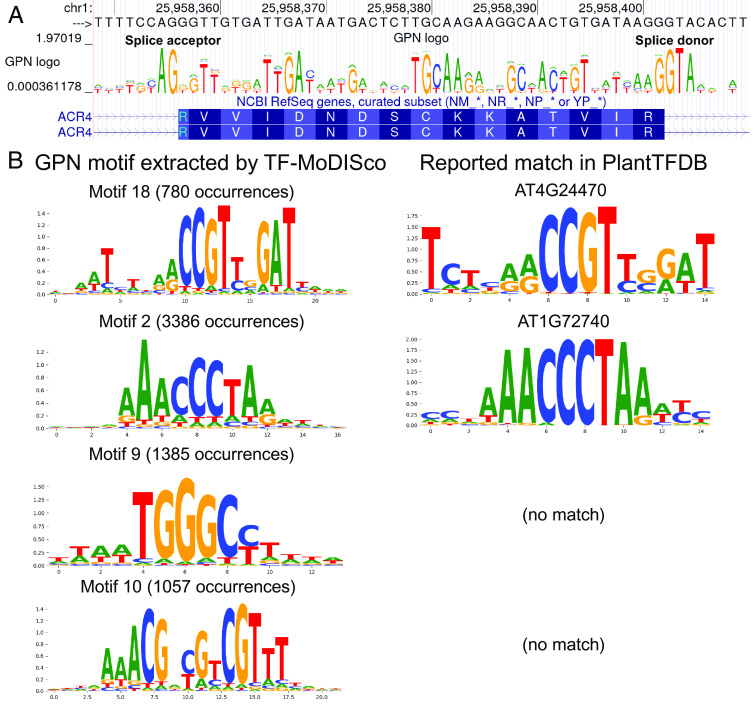
To further understand GPN, we individually masked each position in the genome and obtained the model output distribution over nucleotides, given its context. To facilitate utilizing these predicted distributions, we created sequence logos that can be visualized in the UCSC Genome Browser (34, 35) (https://genome.ucsc.edu/s/gbenegas/gpn-arabidopsis), where the height of each letter is proportional to its probability, and the overall height is given by the information content, measured in bits (36) (see Fig. 3A for an example). The model’s prediction confidence correlates with the expected functionality of the sites. For example, exonic positions are predicted with higher confidence than the surrounding introns, except for the canonical splice acceptor and donor dinucleotide motifs. Similarly, within codons, the third nucleotide position (CDS3), which usually does not affect amino acid identity, is generally predicted with lower confidence than the first two positions (CDS1, CDS2). Start and stop codon motifs are also generally well predicted (examples in SI Appendix, Fig. S3). Across a 1-Mb region in the test chromosome (containing 264 genes and 471 transcripts), model perplexities in splice donors (median $=1.02$), splice acceptors (median $=$ 1.03), start codons (median $=1.08$), CDS2 (median $=2.24$), CDS1 (median $=2.44$), CDS3 (median $=2.79$), and stop codons (median $=2.8$) are significantly smaller than those in intergenic and intronic regions (median $=3.24$, all Mann–Whitney $P$-values $<{10}^{-17}$, SI Appendix, Fig. S4). Perplexity in CDS2 is significantly smaller than that in CDS1, which in turn is significantly smaller than that in CDS3 (all Mann–Whitney $P$-values $<{10}^{-300}$), consistent with their different expected levels of constraint (18).

Fig. 3.

Sequence logos derived from model predictions. Each position in the genome was independently masked and the model distribution over the four nucleotides was computed. (A) Sequence logo visualized in the UCSC Genome Browser (https://genome.ucsc.edu/s/gbenegas/gpn-arabidopsis). The height of each letter is proportional to its probability, while the overall height at each position is equal to 2 minus the entropy of the distribution. (B) Example GPN motifs in promoter regions, extracted by TF-MoDISco, with significant matches in PlantTFDB.

We hypothesized that scanning promoters for small regions of high-confidence GPN predictions could help identify transcription factor binding sites. To achieve this, we adapted TF-MoDISco (37), a tool for de novo identification of transcription factor binding sites using supervised models. This tool clusters high-scoring regions into motifs and compares them to databases of known motifs. Applying the adapted TF-MoDISco to GPN scores in promoter regions, we identified approximately a hundred and sixty motifs (SI Appendix, Fig. S5), with four examples shown in Fig. 3B, the first two having a significant match in PlantTFDB (20) [with $q$-value $<0.05$ in Tomtom (38)]. Some of the identified motifs are well-documented in the literature but do not have a significant match in this database, such as the third motif (39) in Fig. 3B. Some motifs could represent promoter elements not identified previously, like the fourth motif, which is palindromic with symmetrical entropies, suggesting that it could potentially form RNA or DNA alternative secondary structure (40).

Unsupervised Variant Effect Prediction.

GPN can be employed to calculate a pathogenicity or functionality score for any single-nucleotide polymorphism (SNP) in the genome using the log-likelihood ratio between the alternate and reference allele (GPN score, Fig. 1). Visually, this involves comparing the heights of the letters in the logo plot (Fig. 3A).

In silico mutagenesis.

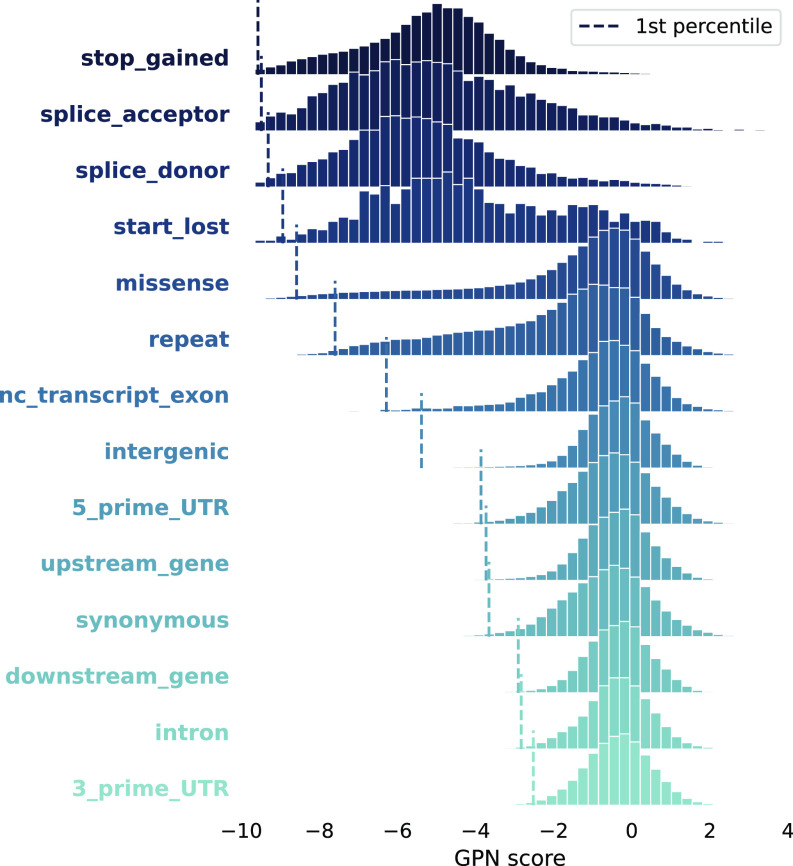
We first computed GPN scores for in silico mutagenesis of SNPs within a 1-Mb region and aggregated the results across variant types (Fig. 4). The ranking of variant types based on the lowest percentile of GPN scores is generally consistent with established notions of deleteriousness (41)^*. For example, the four lowest scored variant types are splice donor, splice acceptor, stop gained, and start lost variants, which significantly disrupt the open reading frame. As expected, missense variants are predicted to have a bigger impact than synonymous variants. However, we observed that some variants within repetitive elements were assigned rather low GPN scores, ranking close to missense variants. Furthermore, the proportion of low GPN scores for repeat variants depends on the training loss weight on repeats (SI Appendix, Fig. S6A). More precisely, in models with 0.0 and 0.1 down-weighting, respectively, 8% and 9% of repeat variants are ranked before the first decile of missense variants. These represent a substantial decrease compared to the 27% observed in the model without any down-weighting (SI Appendix, Fig. S6B, Fisher’s exact test $P<{10}^{-300}$).

Fig. 4.

Variant effect prediction: in silico mutagenesis. Distribution of GPN scores computed for all possible single-nucleotide polymorphisms (SNPs) in a 1-Mb region, across categories, sorted by first percentile (dashed vertical lines).

Benchmarking using allele frequencies in 1001 genomes.

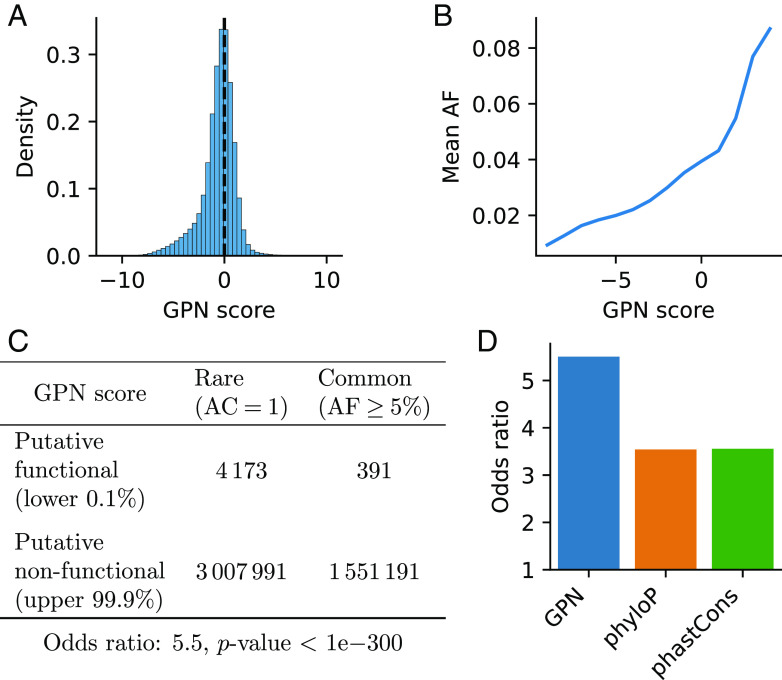
Following our in silico mutagenesis experiments, we analyzed over 10 million SNPs from naturally occurring accessions of the 1001 Genomes Project (42). While most variants have a neutral GPN score, there is a heavy tail of putative functional variants with negative GPN scores (Fig. 5A). Notably, variants with lower GPN scores are, on average, less frequent in the population, suggesting they could be under purifying selection (Fig. 5B, full distribution in SI Appendix, Fig. S7). To evaluate the capability of identifying putative functional variants, we assessed the enrichment of rare versus common variants in the tail of genome-wide score distributions. Putative functional SNPs, defined as the lowest 0.1% of GPN scores, exhibit a 5.5-fold enrichment in rare variants (Fig. 5C); see SI Appendix, Fig. S8 for different allele frequency thresholds. GPN outperforms other genome-wide variant effect predictors for Arabidopsis, specifically phyloP and phastCons, which are conservation scores derived from a broader set of 18 Brassicales species (Fig. 5D). In fact, GPN scores are only weakly correlated with phyloP ($r=0.22,P<{10}^{-300}$) and phastCons ($r=0.13,P<{10}^{-300}$). We also considered the alternative abs(phyloP) (the absolute value of phyloP), but it did not achieve a significant enrichment. A notable advantage of GPN is that it is able to score variants that could not be scored by phyloP and phastCons due to unsuccessful whole-genome alignment (14.2% of all variants). GPN performs comparably to phyloP and phastCons when using less stringent thresholds for defining putative functional SNPs (SI Appendix, Fig. S9), indicating its particular strength in detecting deleterious variants at the extreme tail. GPN also achieves significant odds ratios when computed only within particular variant classes, but its performance relative to phyloP and phastCons varies (SI Appendix, Fig. S9). On a separate note, a slightly higher odds ratio is achieved by the GPN model trained with an intermediate loss weight on repeats (SI Appendix, Fig. S6C). The model trained on only a single species performs substantially worse (SI Appendix, Fig. S10A).

Fig. 5.

Variant effect prediction: rare vs. common. The GPN score was computed for over 10 million variants in the 1001 Genomes. (A) Distribution of GPN scores. (B) Mean allele frequency for different GPN score bins ($[-9.5,-8.5),[-8.5,-7.5),\dots ,[3.5,4.5)$). (C) Contingency table and odds ratio showing enrichment of putative functional GPN scores in rare (AC $=1$) vs. common (AF $\ge 5\%$) variants. AC: allele count. AF: allele frequency. (D) Comparison of odds ratios as in (C) obtained with different models. abs(phyloP) is excluded as it did not achieve a significant enrichment.

Enrichment of GWAS hits in regions with low GPN scores.

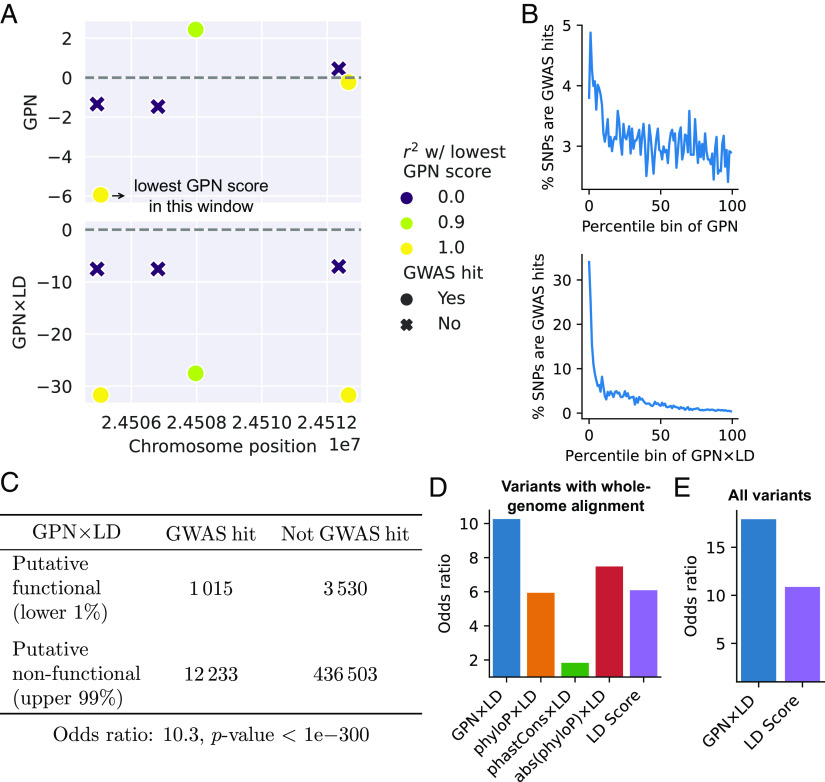
In our pursuit to further evaluate the efficacy of GPN, we examined the AraGWAS Catalog (43), a comprehensive database of GWAS in A. thaliana. We hypothesized that GWAS hits may be enriched in regions with low GPN scores. An advantage of GPN is that it can give substantially different scores to variants in strong linkage disequilibrium (LD) with each other, if their surrounding contexts are different, e.g., Fig. 6A, Top). In contrast, the standard GWAS would give similar scores to such variants; in particular, neutral variants in strong LD with a functional variant would also be associated with a trait. To account for this difference, we devised a score, GPN $\times$ LD, which weighs GPN scores by LD (Materials and Methods). With this approach, GPN $\times$ LD effectively distinguishes GWAS hits from nonhits in this example locus (Fig. 6 A, Bottom). More generally, across the genome and all traits, the tail of GPN $\times$ LD scores is greatly enriched in GWAS hits, much more so than the tail of raw GPN scores (Fig. 6B). In particular, by analyzing odds ratios (Fig. 6C), we found that SNPs with the lower 1% of GPN $\times$ LD scores are 10.3-fold enriched in GWAS hits compared to the upper 99% of GPN $\times$ LD scores, while less than 7.5-fold enrichment was observed for other methods (Fig. 6D); see SI Appendix, Fig. S11 for different thresholds. Using the Bonferroni correction instead of the permutation-based significance threshold recommended by AraGWAS (44) yields lower odds ratios for all methods, but GPN $\times$ LD still achieves the highest enrichment (SI Appendix, Fig. S12). Interestingly, the GPN model trained with an intermediate loss weight on repeats achieves the best performance (SI Appendix, Fig. S6D). The model trained on only a single species performs worse (SI Appendix, Fig. S10B). Furthermore, GPN $\times$ LD achieves much higher odds ratios when considering the full variant set, including regions that do not align to other Brassicales (Fig. 6E); failed alignment could be partly due to genomic rearrangements that may be potentially associated with local adaptation in A. thaliana (45).

Fig. 6.

Variant effect prediction: GWAS. GPN scores were analyzed for around half a million variants tested in AraGWAS. (A) Example window with six variants tested for association with maximum temperature in January. GPN$\times$LD successfully separates GWAS hits and nonhits. (B) Percentage of GWAS hits (for any trait) in each percentile bin of GPN and GPN $\times$ LD scores. (C) Contingency table and odds ratio showing enrichment of GWAS hits (for any trait) in putative functional (associated) GPN $\times$ LD scores. (D) Comparison of odds ratios obtained with different models ($n=453,281$ variants with whole-genome alignment). (E) Odds ratios with the full variant set ($n=510,462$).

Discussion

Here, we present an unsupervised genome-wide variant effect predictor based on pretraining of DNA language models. We demonstrate that GPN outperforms other genome-wide variant effect predictors in A. thaliana, a model species for plant biology. Since GPN is trained only on DNA sequence, it can be readily applied to understudied nonmodel organisms even in the absence of extensive functional genomics data, while still providing state-of-the-art unsupervised variant effect prediction genome-wide.

We can think of GPN as a generalized conservation score. Similar to phyloP and phastCons, GPN is genome-wide, can be trained on genomic sequence alone, and is cell-type and mechanism agnostic (46). The key distinction is that while phyloP and phastCons only consider nucleotide frequencies at a specific site, GPN can learn from joint nucleotide distributions across all similar contexts appearing in the genome. Furthermore, GPN does not rely on whole-genome alignments, which can often have a lower quality in noncoding regions.

The capability of GPN to score genome-wide variants on a unified scale renders it ideal for integration into rare disease diagnosis, fine-mapping, and polygenic risk scores, including burden tests. The separation of genomic regions based on GPN embeddings suggests that it could be further fine-tuned for de novo genome annotation. Combining GPN predictions with TF-MoDISco offers a promising strategy for identifying functional motifs. Although in this study we focused on transcription factor binding sites, we believe that GPN predictions around splice junctions could also facilitate the identification of splicing factor binding sites.

Repetitive elements, which are inherent components of eukaryotic genomes, pose several challenges that have been underexplored in DNA language modeling studies. First, these elements are significantly overrepresented (31). The lower perplexity in nonrepetitive regions upon down-weighting repeats can be attributed to the model allocating fewer parameters exclusively to repetitive elements. Second, repetitive elements display reduced sequence variation compared to other regions, in particular younger repeats with little time to accumulate mutations (47). We believe that these factors together may cause differences in model likelihoods in these regions to be less clearly associated with differences in fitness. Our proposed down-weighting of repeats only partially mitigates these issues, and we encourage further investigation by the scientific community. Potential research directions include examining the effects of down-weighting repeats based on their respective families or inferred age.

While the current implementation of GPN achieves state-of-the-art variant effect prediction for A. thaliana, there is room for improving its training scheme. Mounting evidence suggests that larger models and more extensive training data can enhance performance (48). Our current proof-of-concept model is considerably smaller—by 200 times—than the largest published protein language model (49). One strategy to improve GPN, inspired by protein modeling, involves explicitly incorporating multiple sequence alignments (50, 51). However, this enhancement will be bottle-necked by the quality of alignment in noncoding genome regions. Other promising avenues for DNA language modeling include incorporating DNA-specific inductive biases, such as reverse-complement equivariance (52), as opposed to our current method of averaging model outputs for both strands during testing. Additionally, integrating long-range information using recent advances in state space models (53) may further boost performance. In conclusion, DNA language models represent a powerful framework for genome-wide variant effect prediction, and we believe that exploring the above avenues to further improve GPN would be worthwhile.

Materials and Methods

Pretraining.

We obtained a list of Brassicales reference genome assemblies from NCBI Genome (https://www.ncbi.nlm.nih.gov/data-hub/genome/) ((54)), filtered for RefSeq-annotated and kept only one per genus, resulting in a total of 8 reference genomes (SI Appendix, Table S1). We held out A. thaliana chromosomes 4 and 5 for validation and testing, respectively. For each genome, we subsampled genomic windows of size 512 bp, with a step of 256 bp and augmented with the reverse complement. However, we did not draw genomic windows uniformly from the whole genome, but emphasized certain regions. In particular, we took the union of exons (with a small intronic flank), promoters (1,000 bp upstream of transcription start sites) as well as an equivalent amount of random windows from the whole genome. We think this decision may improve performance, but leave experimentation for further studies. Additionally, we subset the number of windows from each genome to the number of windows from Arabidopsis, given its unusually small genome.

We set up a masked language modeling task (8), in which 15% of the tokens in a nucleotide sequence were masked and had to be predicted from their context. In contrast to most DNA language models that tokenize sequences into overlapping $k$-mers (24, 26, 28) or use byte-pair encoding (23), we used bare nucleotides as tokens. While a thorough benchmark of different tokenization strategies is lacking, using single-nucleotide tokens makes interpretation easier, in particular for unsupervised variant effect prediction.

While language model pretraining successes were first showcased by transformer architectures, convolutional models have shown similarly good performance in natural language (55) and protein modeling (56). In our initial experiments, we noticed that convolutional models converged faster than transformer models. The locality of convolutions may be a good inductive bias for modeling DNA sequences at this scale. The linear complexity of convolution also simplifies inference or fine-tuning on longer sequences such as entire chromosomes, which in the case of transformers might require chunking (with some overlap) and aggregating the results.

We implemented GPN, a convolutional neural network, using the Hugging Face library (57). The masked DNA sequence was one-hot encoded and then consecutively processed by 25 convolutional blocks. Each convolutional block consisted of a dilated convolutional layer followed by a feed-forward layer, with intermediate residual connections and layer normalization (Fig. 1). Throughout the layers, the embedding dimension (number of convolutional filters) was kept fixed at 512. The dilation was increased exponentially up to a certain value and then cycled. A list of hyperparameters is displayed in SI Appendix, Table S3. We trained three models varying only in the loss weight on repetitive elements (marked lowercase in the FASTA file). We trained each model for 150,000 steps, taking approximately 4 d with 4 NVIDIA A100 80 GB GPUs. Perplexity is defined as the exponentiation of the cross-entropy loss, which is equivalent to 1 over the probability given to the correct nucleotide. Test perplexity is displayed in SI Appendix, Table S2. We also trained a separate model on the single genome of A. thaliana, with a repeat weight of 0.1 and the same hyperparameters except for only 12,000 steps with decaying learning rate, as we noticed it would soon start overfitting. This model obtained a higher test perplexity of 3.13 (3.17 on nonrepeat regions).

Analysis of Model Embeddings.

Model embeddings were averaged over nonoverlapping 100-bp windows. Embeddings from the forward and reverse strand were averaged, and then standardized. UMAP was run with default parameters. The gene annotation was downloaded from EnsemblPlants. The annotation of repetitive elements was downloaded from http://ucsc.gao-lab.org/cgi-bin/hgTables?hgsid=167291_E9nY5UIAQRUOAR01xJAsum4vDukw. We considered intergenic regions with 100% overlap with repeats as a separate “Repeat” class. Windows with ambiguous annotation (e.g., 50% CDS and 50% intron) were excluded from the analysis. Genomic region classification was performed with logistic regression as implemented by scikit-learn (58), using class weight inversely proportional to frequency and L2 regularization strength chosen via cross-validation. Windows in each chromosome were predicted by a model trained on the remaining chromosomes.

Motif Analysis.

Each position in the genome was independently masked and the model distribution over nucleotides was extracted. The distribution was averaged between the results from the forward and reverse strands. The held-out model perplexity was computed for splice acceptors, splice donors, start codons, stop codons, CDS, and intergenic and intronic positions in the 1-Mb region Chr5:3,500,000-4,500,000, after excluding repeats.

An adaptation of TF-MoDISco was run with model predictions in regions 1,000 bp upstream and downstream of transcription start sites (all chromosomes), after filtering repeats and coding exons. The exact score fed into TF-MoDISco was the nucleotide probability minus 0.25, so it would be roughly centered at 0. Since TF-MoDISco expects genomic windows of equal length, we concatenated our variable-length windows into one large window, interspersed with 20 undefined “N” nucleotides.

Variant Effect Prediction.

We scored variants by masking the position and calculating the log-likelihood ratio between the alternate and reference allele. Scores computed from the forward and reverse strands were averaged. We calculated the odds ratio and $P$-value with Fisher’s exact test. When comparing to phyloP and phastCons, we excluded variants where these scores are undefined (due to the lack of whole-genome alignment).

All possible SNPs in the region Chr5:3,500,000-4,500,000 were generated and their consequences annotated with Ensembl Variant Effect Predictor (41) web interface https://plants.ensembl.org/Arabidopsis_thaliana/Tools/VEP, with the upstream/downstream argument set to 500, used to call variants as upstream/downstream instead of intergenic. We compared scores for variant types with at least 1,000 variants, and we excluded variants with different consequences in different transcripts.

The 1001 Genomes genotype matrix was downloaded from https://aragwas.1001genomes.org/api/genotypes/download ((59)) and combined with metadata from https://1001genomes.org/data/GMI-MPI/releases/v3.1/1001genomes_snp-short-indel_only_ACGTN.vcf.gz. This genotype matrix is binary, since all the accessions are homozygous, as Arabidopsis is predominantly selfing. For variants with alternate allele frequency greater than 50%, we flipped the sign of GPN scores (equivalent to taking the log-likelihood ratio between the minor and the major allele) and did all analyses in terms of minor allele frequency. Variant consequences produced by Ensembl Variant Effect Predictor were downloaded from Ensembl Plants. Conservation scores were downloaded from http://plantregmap.gao-lab.org/download.php#alignment-conservation ((60)). For conservation scores phyloP and phastCons, we simply flipped the sign to obtain a variant score, i.e., variants at conserved sites should be considered more pathogenic. We additionally scored variants using (minus) the absolute value of phyloP, referred to as abs(phyloP), which means prioritizing putative accelerated regions over putative neutral ones. We defined rare variants as those with allele count equal to 1 (to be precise, it is two alleles in the same homozygous accession), and common variants as those with allele frequency above 5%. Model scores were defined as pathogenic or benign based on a quantile threshold that we varied from 0.1% to 10%.

GWAS summary statistics for all 462 phenotypes were downloaded through the AraGWAS API, with the default threshold of minimum allele count of 6 (i.e., at least 6 homozygous accessions having the allele). The summary statistics include information on whether an association is significant according to a permutation-based approach recommended (44) as well as a Bonferroni threshold. The LD matrix of squared Pearson correlations ($r^2$) was calculated within a radius of 100 kb around each variant, using sgkit (https://pystatgen.github.io/sgkit/). We define a weighted sum of GPN scores according to LD ($i$ and $j$ index SNPs):

$$\text{GPN}\times {\text{LD}}_i=-{\displaystyle \sum _j}|{\text{GPN}}_j|·r_{\mathit{ij}}^2.$$

This is known as a stratified LD Score (61) and can also be interpreted as the multiplication between the LD matrix and the vector of GPN scores. The reason why we used unsigned LD and model scores is that we focused on assessing whether a variant would have a significant association with differences in a trait, regardless of the direction of the association. Since the association $P$-value is invariant to recoding of reference and alternate alleles, we took the absolute value of GPN scores. We arbitrarily added a negative sign in front to be consistent with more negative implying more likely functional. We similarly defined phyloP $\times$ LD (first shifting the scores to reside entirely on the negative side of the number line), abs(phyloP) $\times$ LD and phastCons $\times$ LD. We considered the baseline LD Score (62), the unweighted sum of LD with a given variant:

$$\text{LD}{\text{Score}}_i={\displaystyle -\sum _j}{r}_{\mathit{ij}}^2.$$

Use of AI Software.

ChatGPT was used to improve the wording of some paragraphs, but not to generate new content.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Code to reproduce all results, including instructions to load the pretrained model, is available at https://github.com/songlab-cal/gpn (63). All other data are included in the manuscript and/or SI Appendix. Previously published data were used for this work (https://www.ncbi.nlm.nih.gov/data-hub/genome/ (54), https://aragwas.1001genomes.org/api/genotypes/download (59), and http://plantregmap.gao-lab.org/download.php#alignment-conservation (60)).