A polygenic explanation for Haldane’s rule in butterflies

Significance

In 1922, J.B.S. Haldane observed higher frequencies of defects in animal hybrids of the heterogametic sex (XY-males or ZW-females). He proposed it as a general rule, later verified across diverse animals. However, genomic analyses of Haldane’s rule rarely include female heterogametic taxa such as butterflies. We map female-biased hybrid defects in butterflies to identify genes underlying Haldane’s rule. Surprisingly, most defects map to numerous sex chromosome factors of small individual effects. Yet, their combined effects become significant and can explain Haldane’s rule. We also demonstrate how numerous small-effect factors on a single chromosome can appear as spurious large-effect loci. This mapping artifact persists even for large samples and dense markers and may cause underreporting of polygenicity from genetic crosses.

Abstract

Two robust rules have been discovered about animal hybrids: Heterogametic hybrids are more unfit (Haldane’s rule), and sex chromosomes are disproportionately involved in hybrid incompatibility (the large-X/Z effect). The exact mechanisms causing these rules in female heterogametic taxa such as butterflies are unknown but are suggested by theory to involve dominance on the sex chromosome. We investigate hybrid incompatibilities adhering to both rules in Papilio and Heliconius butterflies and show that dominance theory cannot explain our data. Instead, many defects coincide with unbalanced multilocus introgression between the Z chromosome and all autosomes. Our polygenic explanation predicts both rules because the imbalance is likely greater in heterogametic females, and the proportion of introgressed ancestry is more variable on the Z chromosome. We also show that mapping traits polygenic on a single chromosome in backcrosses can generate spurious large-effect QTLs. This mirage is caused by statistical linkage among polygenes that inflates estimated effect sizes. By controlling for statistical linkage, most incompatibility QTLs in our hybrid crosses are consistent with a polygenic basis. Since the two genera are very distantly related, polygenic hybrid incompatibilities are likely common in butterflies.

Speciation is a complex process, yet it obeys empirical rules across taxa with sexual reproduction (1). Haldane’s rule states that among hybrids between different species, the heterogametic sex (the sex with XY or ZW sex chromosomes) tends to have lower fitness (2, 3). A second rule is the large-X/Z effect, which states that the sex chromosome is disproportionately involved in hybrid incompatibility (1, 4). Haldane’s rule is entirely phenomenological, but it holds across many phylogenetically diverse organisms (5–7). Whether adherence to Haldane’s rule emerges from a common set of genetic mechanisms is an open question (8). The large-X/Z effect also appears robust, but without mapped incompatibility factors, the evidence is often indirect and hard to interpret (9–13).

Several mechanisms can explain Haldane’s rule. First, dominance theory posits that the single X/Z chromosome in the heterogametic sex might expose recessive genes that are deleterious in a hybrid genetic background, thus facilitating incompatibility (4, 14). Second, the evolution of sex chromosomes may be faster than autosomes; thus, Haldane’s rule can be produced via multiple processes involving hemizygous haploid selection (15), sex-specific selection (16), and sex chromosome conflict (17, 18). Accelerated sex chromosome evolution also provides a natural explanation for the large-X/Z effect. Empirical evidence for these mechanisms comes from mostly male heterogametic taxa, such as mammals and Drosophila (19, 20), but how general these explanations for the two rules are is unknown. It has also been suggested that spermatogenesis is particularly prone to disruption, which can explain the higher incidence of sterility in XY males (21), but this is not applicable to Haldane’s rule in ZW females (7).

In Lepidoptera (butterflies and moths), the female is the heterogametic sex (with ZW sex chromosomes), and hybrid females are more prone to defects than males (2, 22). To date, little is known about the genetic basis of Haldane’s rule in Lepidoptera, except for a few studies using sparse genetic markers (23–25) and a recent whole-genome Quantitative Trait Locus (QTL) study in Heliconius (26). Nonetheless, these studies demonstrate that hybrid female sterility maps to the Z chromosome, consistent with a large-Z effect. Here, we study hybrid incompatibility between two closely related butterflies, Papilio bianor and Papilio dehaanii (Fig. 1A). Their interspecific crosses produce fertile males but completely sterile females (27, 28). Hybrids also develop abnormal body size, as observed in other Papilio hybrids (29). To test for the genetic basis of the two rules in this system, we conduct QTL studies of body size (pupal weight) and female reproduction (ovary dysgenesis) in backcross hybrids. We then compare Papilio with Heliconius (26) to test whether these genera share a similar genomic basis for the two rules.

Fig. 1.

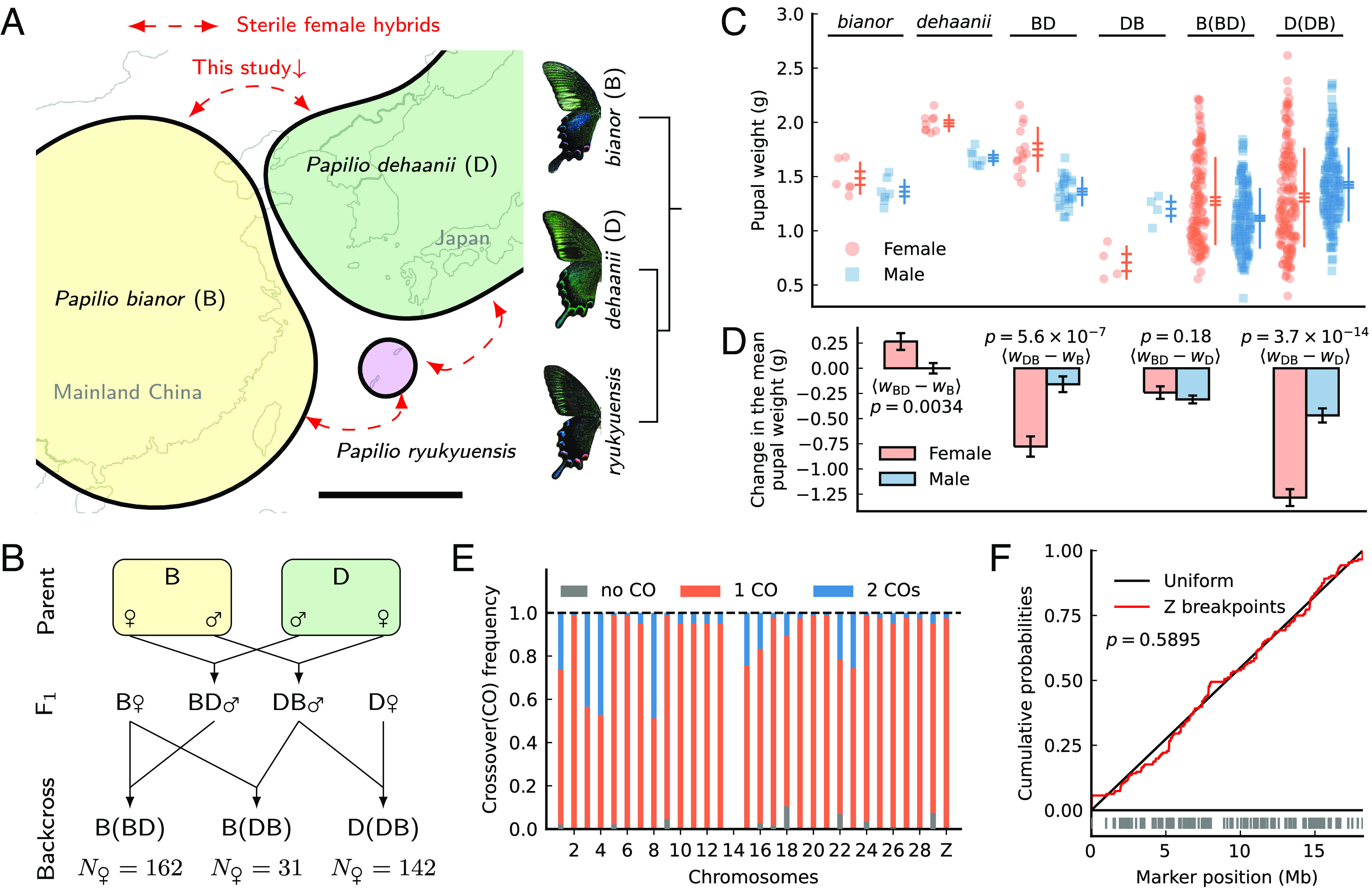
The study design, variation in pupal weight, and patterns of meiotic crossover in Papilio. (A) Geographic distribution and species relationships in the P. bianor complex (Scale bar; 1,000 km). (B) Crossing design. (C) Pupal weight variation among parents, F₁s, and backcrosses. Horizontal bars represent the mean ± SE. Vertical lines represent the mean ± SD. (D) Changes in mean pupal weight between F₁s and parents in each sex. Error bars are standard errors of the mean changes. The significance of male vs. female differences is shown as P-values of Z-tests. (E) The crossover frequency in F₁ males per chromosome pair per meiosis. Chr14 is excluded due to assembly problems. (F) Recombination breakpoints on the Z chromosome are uniformly distributed (the P-value is from a Kolmogorov–Smirnov test). Vertical bars are inferred breakpoints.

Results

Haldane’s Rule between P. bianor and P. dehaanii.

To investigate hybrid phenotypes, we performed reciprocal F₁ crosses and backcrosses between the two species (Fig. 1B). We follow the order (female×male) in notation. For instance, “B(BD)” is equivalent to “bianor×(bianor×dehaanii)”, where “B” and “D” stand for bianor and dehaanii, respectively.

Pupal weight (W) is treated as a proxy for adult body size. F₁ females with a dehaanii mother (“DB”) are significantly smaller than females of either parental species, but in the reciprocal cross with a bianor mother (“BD”), they span the range of parental females (Fig. 1C). For F₁ males, deviation in pupal weight from parental males is less extreme than that of F₁ females (Fig. 1D). We interpret female-biased abnormal size as a defect conforming to Haldane’s rule.

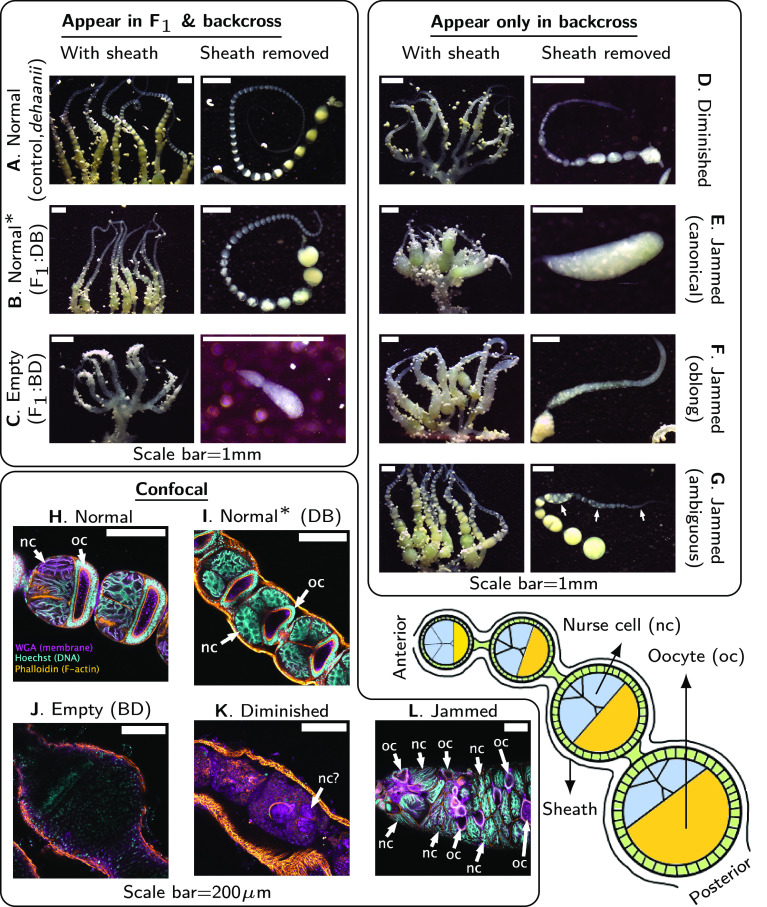
Focusing on hybrid female sterility, we dissected ovaries across the pedigree and determined major ovary phenotypes (Fig. 2). To our surprise, while F₁ females with a bianor mother (“BD”) have almost empty ovaries (Fig. 2 C and J), F₁ females in the reciprocal cross (“DB”) develop and lay superficially normal eggs (Fig. 2 B and I). However, eggs laid by mated females never hatch. We score ovary phenotype rather than female fertility per se: Ovaries with regularly spaced and spherical follicles are subsequently all classified as “Normal.” Since deformed ovaries lead to sterility and can be readily scored, this is a sufficient and efficient approach to detect sterility factors.

Fig. 2.

Ovary morphology supports a categorical classification of phenotypic defects in Papilio. Monochrome confocal images for each channel are in SI Appendix, Figs. S1 and S2 (WGA stains membranes in magenta; Hoechst stains DNA in cyan; Phalloidin stains F-actin in orange). A schematic diagram of butterfly ovarioles is shown at the bottom right. Scale bars for stereoscope images are approximate (Materials and Methods, Phenotyping Ovaries). Sheath is removed in panels H and L. (A) Phenotype Normal in a pure individual. (B) Phenotype Normal in F₁ females of the cross DB. (C) Phenotype Empty in F₁ females of the cross BD with little tissue inside sheath. (D) Phenotype Diminished with a substantial amount of interior tissue without discernible follicle structures. (E–G) Phenotype Jammed. Follicle cells fuse into tubes with many nurse cells and oocytes. Subtype canonical: Each ovariole collapses into a single tube of oocytes and nurse cells. Subtype oblong: Tubes are elongated. Subtype ambiguous: Tubes and isolated follicles coexist. (H–L) The same phenotypes imaged using confocal microscopy. Sheath is removed in panels H and L.

Since ovary and female size phenotypes differ significantly between reciprocal crosses, hybrid incompatibility in this system likely involves asymmetrically inherited genetic elements (“Darwin’s Corollary”) (30). For this reason, we separate backcross types according to maternal origin in QTL analysis.

Single Meiotic Crossovers on the Z Chromosome in F₁ Males.

To infer haplotypes and crossover patterns, we carried out whole-genome low-coverage ($\sim$1×) sequencing in backcrosses, while F₁s and parents were sequenced to higher depths (>5× and >30×, respectively). Prior to crossover analysis, we used linkage information from all families to correct assembly errors in the reference genome of P. bianor (31), except for chromosome 14, where errors remained unresolved (SI Appendix, Fig. S4). As assembly errors can affect inference of recombination breakpoints, we do not report crossover patterns on chromosome 14.

We inferred the crossover pattern in F₁ males by counting the estimated recombination breakpoints across all backcross offspring (female meiosis in Lepidoptera lacks crossovers). Most F₁ males had at least one crossover per chromosome pair per meiosis, but the degree of crossover interference varied among chromosomes (Fig. 1E). Double crossovers were frequent on some chromosomes but very rare on most. Importantly, the Z chromosome in the Papilio crosses had almost no double crossovers, and its recombination breakpoints were approximately uniformly distributed (Fig. 1F). Therefore, recombination on the Z chromosome in Papilio F₁ males can be modeled by single crossovers uniformly distributed along the chromosome. In Heliconius F₁ males, crossover on the Z chromosome is single but spatially nonuniform (26). We apply the single crossover model to the study of incompatibilities.

Polygenic Basis of Abnormal Pupal Weight on the Z Chromosome in Papilio.

Pupal weight in offspring of B(BD) and D(DB) backcrosses has a broad distribution exceeding the parental range (Fig. 1C). Single-marker QTL scans suggest that the Z chromosome alone controls pupal weight variation in females (Fig. 3A), consistent with a large-Z effect. These scans reveal a major QTL near the center of the Z chromosome in both backcrosses, explaining over 50% of the phenotypic variance (SI Appendix, Fig. S8). Nonetheless, we reason below that this major QTL is likely a statistical artifact caused by multiple factors scattered across the Z chromosome.

Fig. 3.

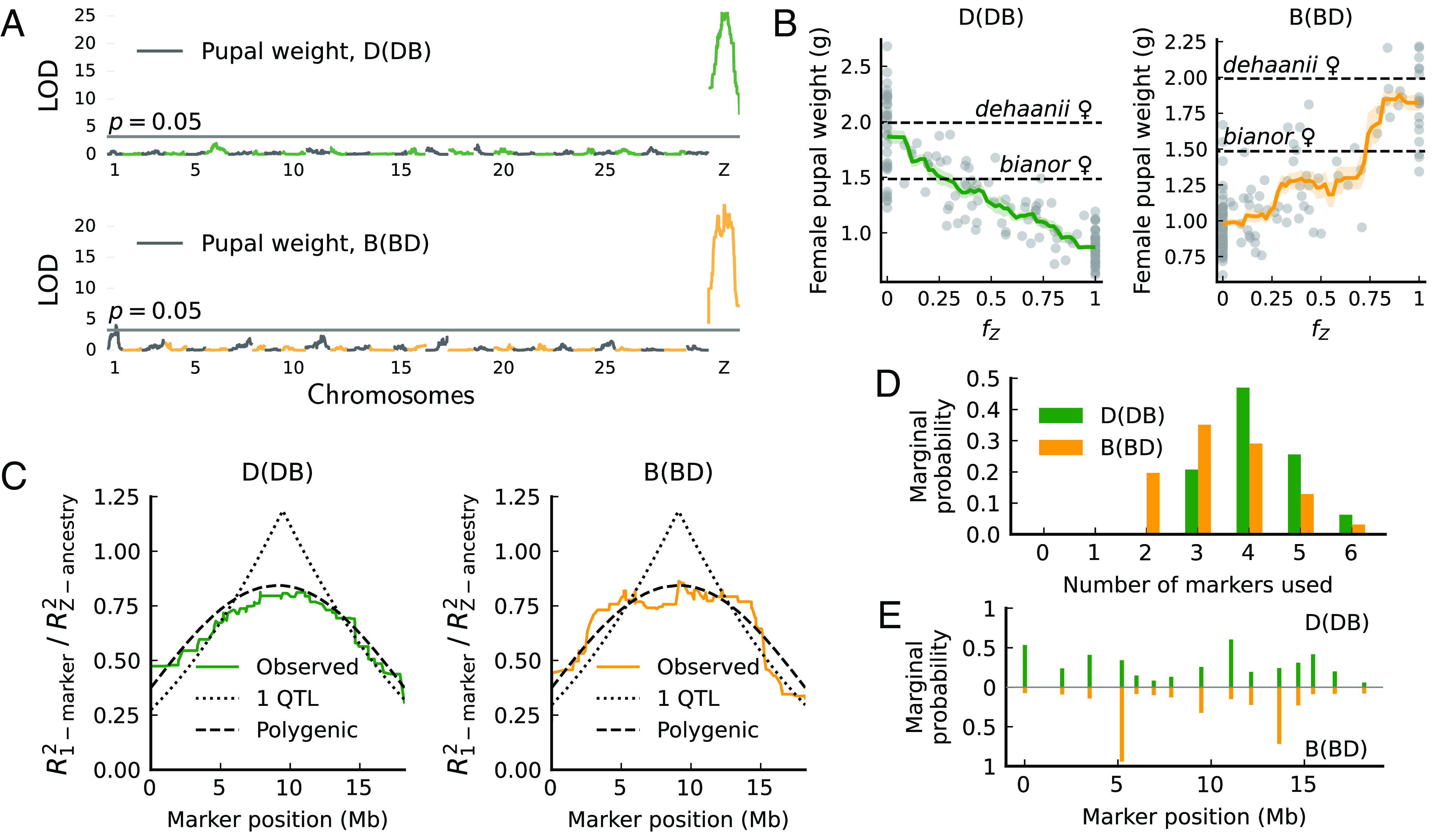
Pupal weight variation in female hybrids maps to many additive Z-linked effects in Papilio. (A) One-dimensional QTL scan shows that variation in pupal weight is mainly explained by the Z chromosome. LOD scores peak at the Z chromosome center. Alternating colors represent different chromosomes. (B) Introgressed ancestry fraction on the Z chromosome ($f_Z$) is highly informative of pupal weight (adjusted by brood). (C) Genotype–phenotype regression does not support any 1-QTL architecture for pupal weight. The distribution of regression power is measured by $R_{\text{1-marker}}^2/R_{\text{Z-ancestry}}^2$ (the ratio between $R^2$ using a single marker versus a polygenic model of Z chromosome ancestry). The polygenic model provides a better fit for the observed curves. (D and E) Bayesian QTL model selection (33) based on 15 sparsely spaced markers favors the simultaneous inclusion of multiple markers ($\ge$3) in predicting pupal weight. Markers more favored by models have higher marginal probabilities of being selected. Marginal probabilities equal the partial sum of the posterior probabilities of QTL models.

The following evidence supports Z-linked polygenic architecture. First, pupal weight changes almost monotonically with the fraction of introgressed ancestry on the Z chromosome (Fig. 3B; from here on, the introgressed Z-chromosome ancestry fraction is denoted as $f_Z$ and the introgressed autosomal ancestry fraction as $f_A$). This shows that $f_Z$ is informative in predicting pupal weight. Second, genetic variance of pupal weight is much smaller than that expected for a single QTL of major effect but is more in line with a linear polygenic model in which weight varies linearly with $f_Z$ (Table 1). Thus, multiple additive factors may be involved. Third, we compare features of genotype–phenotype associations between these two extreme genetic architectures: a single-QTL model versus a linear polygenic model. Given the polygenic model, the strength of association ($R^2$) will always be larger for models using $f_Z$ (i.e., $R_{\text{1-marker}}^2/R_{\text{Z-ancestry}}^2<1$ for all markers). Conversely, given the single-QTL model, markers tightly linked to the QTL will surpass $f_Z$ in association strength (i.e., $R_{\text{1-marker}}^2/R_{\text{Z-ancestry}}^2>1$ for some markers). Using the approximate crossover model, we derive $R_{\text{1-marker}}^2/R_{\text{Z-ancestry}}^2$ on the Z chromosome analytically under each architecture (SI Appendix, section 2), and the observed patterns closely resemble polygenic predictions (Fig. 3C). Fourth, Bayesian QTL model selection (32) also favors multiple additive markers in predicting pupal weight (Fig. 3D). Posterior probabilities for markers being selected are more evenly distributed in D(DB) females (Fig. 3E, Top), congruent with a near-linear relationship between pupal weight and $f_Z$ (Fig. 3B, Left). For B(BD) females, this relationship is less smooth (Fig. 3B, Right), and a two-QTL model is a slightly better fit to the observed $R_{1-\mathrm{marker}}^2/R_{\mathrm{Z}-\mathrm{ancestry}}^2$ curve than the linear polygenic model (SI Appendix, Fig. S9). In either case, the apparent large-effect QTL at the chromosome center is a statistical mirage caused by more than one additive factor scattered on the Z chromosome.

Table 1.

Genetic variance of pupal weight (V_g, unit: g²)

Backcross direction	D(DB)	B(BD)
Expected Vg for a single QTL	0.250	0.168
Expected Vg for a linear polygenic model	0.166	0.112
Observed Vg	0.136	0.0977

The polygenic model offers an intuitive explanation for the apparent center QTL: For single and spatially uniform crossovers, ancestries of central markers have the highest correlation with $f_Z$ (SI Appendix, Theorem 2). If phenotype varies linearly with $f_Z$, central markers also provide the richest phenotypic information, generating the apparent QTL. Thus, our evidence is highly consistent with a polygenic architecture of abnormal pupal weight, rendering the introgressed Z-chromosome ancestry fraction informative in predicting phenotypes.

Polygenic Basis of Ovary Dysgenesis on the Z Chromosome.

Ovary dysgenesis leads to hybrid female sterility. Previously, this sterility in Heliconius butterflies was mapped to a pair of epistatic QTLs near each end of the Z chromosome in the backcross from H. pardalinus sergestus to H. p. butleri (Fig. 4A, Left) (26). That study also suggested a weak single-locus QTL at the Z chromosome center (Fig. 4B, Top). In Papilio D(DB) females, we also identified a pair of epistatic QTLs on the Z chromosome for phenotype “Normal” (Fig. 4A, Right), but no single-locus QTL on the Z chromosome (Fig. 4B, Bottom).

Fig. 4.

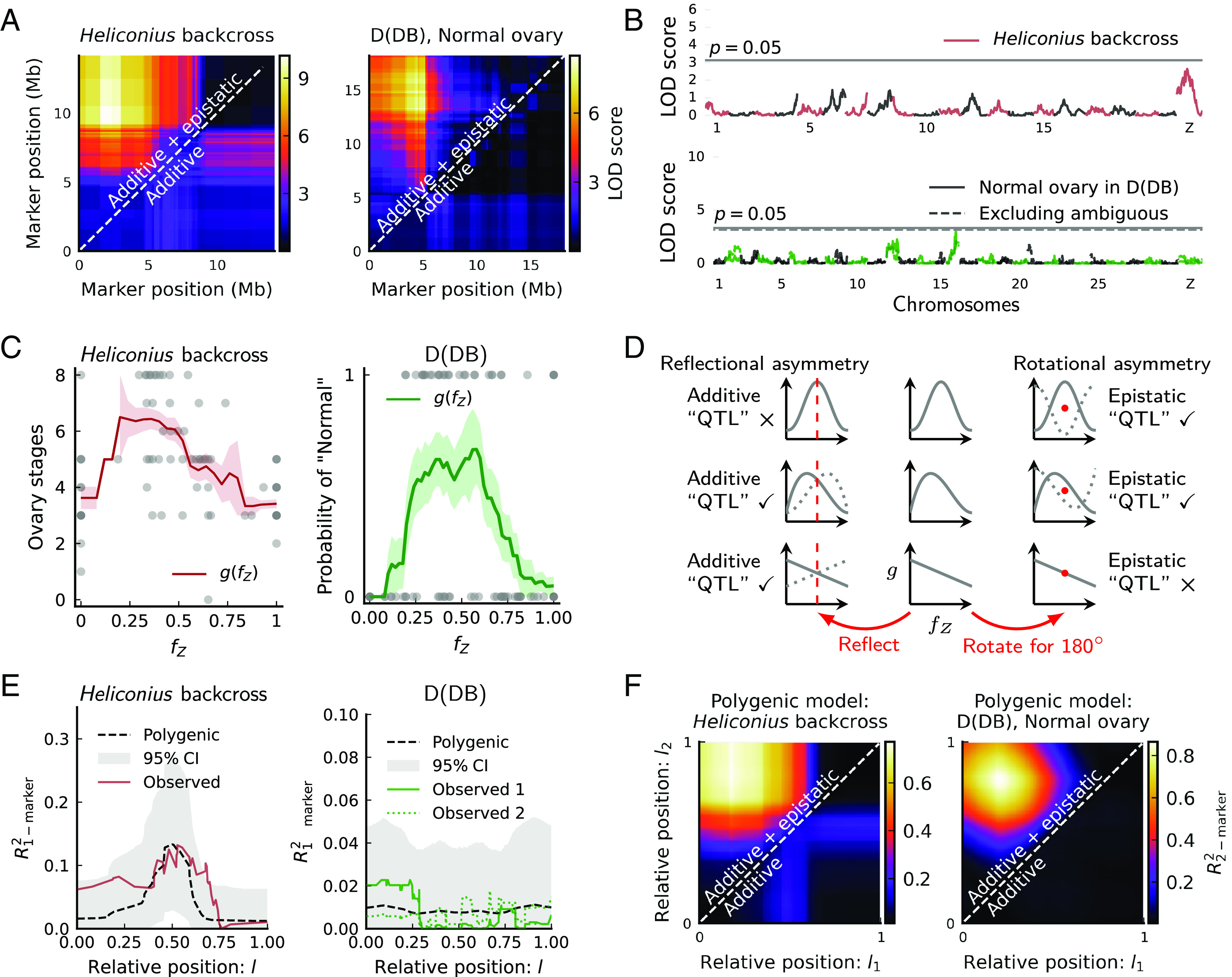
The polygenic basis of ovary dysgenesis in Heliconius backcrosses and Papilio-D(DB) females. (A) Two-marker scans identify epistasis between the Z chromosome ends. (B) One-marker scans identify a weak additive QTL on the Z chromosome in Heliconius. No significant additive QTL on the Z chromosome in D(DB) females. (C) Introgressed ancestry fraction on the Z chromosome ($f_Z$) is informative of ovary phenotype. Higher scores in Heliconius are more “normal.” The moving average of phenotype scores (window size$=$0.2) represents $g(f_Z)$. Shaded areas are means $\pm$ SEs. Dots in D(DB) represent one round of phenotype assignment. (D) For traits fully polygenic on a chromosome, QTL analysis in backcrosses via marker-phenotype regression reveals only the asymmetry in $g(f_Z)$. The middle column shows three representative polygenic models. The dotted curves on the left are produced by reflecting each model with respect to its center line. The dotted curves on the right are produced by rotating each model with respect to its center point for 180${}^{°}$. Asymmetry ensues when the dotted curve does not overlap fully with the original model, which produces additive and/or epistatic QTLs depending on asymmetry types. (E) Polygenic models predict the results of one-marker scans. Dashed curves and shaded areas represent the means and 95% CIs of $R_{\text{1-marker}}^2$, across 10,000 simulated backcross broods matching sample sizes ($N_{\text{Heliconius}}$ = 86, $N_{\text{D(DB)}}=$142). For D(DB), observed 1 classifies ambiguous individuals as “Normal,” while observed 2 classifies them as the opposite. (F) Polygenic models yield apparent epistasis in two-marker scans—compare Fig. 4A. Heatmaps show the means of $R_{\text{2-marker}}^2$ across 100 simulated backcross broods matching sample sizes.

We argue, however, that the architecture may again be polygenic on the Z chromosome for both cases and that the apparent QTLs on the Z chromosome are likely statistical artifacts. This is indicated first by the fact that $f_Z$ predicts ovary phenotypes: Backcross females in Heliconius and Papilio (“D(DB)”) develop more normal ovaries when the Z chromosome has intermediate levels of $f_Z$, while extreme levels of $f_Z$ coincide with abundant defects (Fig. 4C and SI Appendix, Figs. S11 and S13). To reconcile polygenicity with apparent QTLs, we assume a general polygenic model in which the expected phenotype is a continuous function $g$ of $f_Z$. In practice, $g$ is the moving average of phenotypic scores with respect to $f_Z$ (Fig. 4C). Again, if phenotypes depend only on introgressed ancestry fraction, a significant QTL does not necessarily imply a major effect of the identified locus in development. Rather, we show that these QTLs can arise indirectly from the asymmetry in polygenic models (Fig. 4D and SI Appendix, section 3). Specifically, conditioning on a polygenic model $g(f_Z)$, and for an arbitrary positioning of single crossovers in backcrosses, we prove that

1. Additive single QTLs are caused by the reflectional asymmetry in $g(f_Z)$ with respect to its center (Fig. 4D, Left. See SI Appendix, Theorems 6–8 and Fig. S12)

2. Epistatic QTL pairs are caused by the rotational asymmetry in $g(f_Z)$ with respect to its center (Fig. 4D right. See SI Appendix, Theorems 9 and 10, and Fig. S14)

With these relations, a polygenic architecture on the Z chromosome can be tested by comparing predicted vs. observed QTLs. For both cases of ovary dysgenesis, $g$ has a unimodal form (Fig. 4C). This form is strong in rotational asymmetry but weak in reflectional asymmetry (e.g., the first two rows in Fig. 4D). Consequently, it predicts apparent strongly epistatic QTLs but no or only weak additive QTL, as observed (Fig. 4E and F). In contrast, the $g$ for pupal weight is largely linear, which is reflectionally asymmetric but rotationally symmetric (e.g., the last row in Fig. 4D). This shape correctly predicts a major additive QTL at the chromosome center (Fig. 3C) and no epistatic QTLs (SI Appendix, Fig. S10). Thus, the polygenic architecture recovers the strength of marker-phenotype association across the Z chromosome and can explain the presence of both additive and epistatic apparent QTLs. This reasoning therefore is congruent with the hypothesis that Z-linked hybrid sterility effects are polygenic and corroborates the polygenicity of Z-linked weight effects.

Modulation of Incompatibilities by Autosomal Backgrounds.

Epistasis between chromosomes is a common mechanism for hybrid incompatibility (33–35). We show below that Z-linked incompatibilities in our systems also have autosomal components. For pupal weight, if Z-linked weight effects were independent of genetic background, F₁ females between a P. dehaanii mother and a P. bianor father should be of a similar size to normal P. bianor. Instead, they are much smaller than either parental female (Fig. 1C), suggesting epistasis between the P. bianor Z chromosome and the F₁ genomic background. Likewise, pupal weight decreases beyond the parental range in both backcrosses, which are of opposite maternal backgrounds, when the Z chromosome comes entirely from P. bianor (Fig. 3B). This evidence corroborates that Z-linked weight effects likely result from epistasis between the P. bianor Z chromosome and hybrid autosomes—perhaps autosomal regions inherited from P. dehaanii. On the other hand, the P. dehaanii Z chromosome does not seem to interact with a hybrid autosomal background. This is consistent with mostly normal pupal weights in BD females, D(DB) females with $f_Z=0$, and B(BD) females with $f_Z=1$. Similarly, ovaries are defective in Heliconius as well as Papilio D(DB) backcrosses even when the Z chromosome comes entirely from the maternal species (Fig. 4C), consistent with a significant role of autosomal introgression in ovary defects. When autosome-only introgression causes defects, normal phenotypes are very rare (e.g., individuals with $f_Z=0$ in Figs. 3B, Right and 4C). Therefore, multiple autosomal incompatibility factors are likely present to sustain a high frequency of defects. These results suggest that autosomal components of incompatibility are also somewhat polygenic and may depend on the introgressed autosomal ancestry fraction. Nonetheless, there are many autosomes in both butterflies (29 in Papilio and 20 in Heliconius). The autosomal effect is thus difficult to detect among backcrosses because variation of $f_A$ is much smaller than that of $f_Z$.

Exceptions to Polygenic Architecture.

The polygenic architecture we have found, however, does not apply to all incompatibilities in Papilio. In females with a P. bianor mother, introgression of a small region ($\sim$1 Mb) on the Z chromosome from P. dehaanii is sufficient to cause the ovary defect “Empty” (SI Appendix, Fig. S15A and Table S1). This phenotype obliterates nearly all follicle tissues (Fig. 2 C and J), effectively overriding all milder defects. In this maternal background, a small region on chromosome 8 also modulates the development of the “Normal” ovary phenotype (SI Appendix, Fig. S15B and Table S1). These results suggest that ovary dysgenesis in Papilio hybrids with a P. bianor mother is predominantly affected by narrow genomic regions of large effect, in contrast to the polygenic architecture in the opposite maternal background.

Discussion

Dominance Theory is Insufficient.

Dominance theory requires sex-linked incompatibility factors to be mostly recessive so that the homogametic sex is sheltered by dominance (7, 14). This theory is applicable to Lepidoptera but does not explain our observation. First, dominance theory implies that many Z-linked polygenes should be simultaneously recessive, which is untested in Lepidoptera. Second, an intermediate level of introgression on the Z chromosome ameliorates ovary defects in backcross females (Fig. 4C). This is unexpected under dominance theory because intermediate levels of introgression would still expose recessive Z-linked factors in females to cause defects. Third, backcross males in Papilio have only heterozygous introgression, so their large variation in pupal weight disproves universally recessive Z-linked factors (Fig. 1C). Faster-Z theory also has little support: The $dN/dS$ ratio is similar between the Z chromosome and autosomes in Heliconius (26), and sequence divergence in Papilio is even larger on the autosomes than the Z chromosome (SI Appendix, Fig. S16).

A Polygenic Explanation for Two Rules of Speciation.

Polygenic incompatibilities are, however, reminiscent of mechanisms based on asymmetric inheritance (30). Recall that $f_Z$ and $f_A$ are the introgressed ancestry fractions on the Z chromosome and on all autosomes, respectively. Since Z-linked polygenic effects arise from epistasis with autosomes, a balancing process appears to exist between ancestry on autosomes and on the Z chromosome: Phenotypes degrade when $f_Z$ and $f_A$ deviate from optimal balance. In Heliconius backcrosses, this balance appears to be $f_Z=f_A$ ($f_Z\sim 0.25,f_A\sim 0.25$), which correctly predicts that F₁ ovaries are defective ($f_Z=1,f_A=0.5$) (26). This optimal balance may take other forms for different traits. For instance, in Papilio, most “Normal” ovaries in D(DB) females coincide with $f_Z=2f_A$ ($f_Z\sim 0.5,f_A\sim 0.25$), which also predicts correctly that DB females ($f_Z=1,f_A=0.5$) have “Normal” ovaries. For pupal weight, the balance ensues when there is minimal coexistence between the P. bianor Z chromosome and the P. dehaanii autosomes. Our balance explanation is ancestry-based and naturally requires a polygenic genetic basis.

Now, explaining the two rules of speciation becomes explaining the likelihood of imbalance in each sex and its genetic underpinning. The key insights are

1. $f_Z$ is more skewed from $f_A$ in F₁ females than in F₁ males;

2. $f_Z$ is much more variable than $f_A$ in backcrosses;

3. The Z chromosome is shorter than all autosomes combined;

4. $f_A$ is reduced in backcrosses compared to that in F₁ hybrids.

Thus, 1) implies that F₁ females are likely more unbalanced than F₁ males, generating Haldane’s rule in certain balance conditions (e.g., abnormal pupal weight for DB females); 2) implies that variation of imbalance among backcrosses is largely attributable to the Z chromosome, generating a large-Z effect in backcross mapping; 3) implies that an introgressed element of a fixed physical length can change $f_Z$ (if on the Z chromosome) more than $f_A$ (if on an autosome)—This predicts a large-Z effect in introgression lines; and 4) implies that the optimal $f_Z$ may differ between F₁ and backcrosses.

Our explanation resembles earlier theories of Haldane’s rule based on sex-autosome imbalance^* (2, 34, 36), does not require dominance, and is in principle just as applicable to male heterogametic taxa ($f_X$ vs. $f_A$). However, in light of multiple causes of Haldane’s rule in other taxa (8), it is likely that our mechanism explains some but not all Lepidopteran hybrid incompatibilities. After all, some hybrid defects are clearly caused by narrow regions on the Z chromosome in our crosses.

Molecular Mechanisms of Polygenicity.

The molecular nature of polygenicity is unresolved. In our case, it is tempting to consider epigenetic mechanisms between autosomes and the Z chromosome. For instance, genetic variance of pupal weight in backcross males is much smaller than that in females (SI Appendix, Table S2). This is consistent, for instance, with dosage compensation in Lepidoptera in which both Z chromosomes in males are partially suppressed (37), which will dampen the effects of introgressed factors.

Spurious QTLs of Highly Polygenic Traits.

We find that QTL analysis of highly polygenic traits can produce spurious major effect loci using crosses with long ancestry tracts even with large sample sizes and dense markers. Here, “ghost” QTLs likely result from the cumulative influence of polygenes linked to focal markers, and the peaks in association strength do not result from a major single locus effect in development. This problem has been well recognized in QTL theories despite a lack of universal solutions (38–41). Still, empirical analyses rarely consider this complexity because common software assumes only one or two QTLs per chromosome (42, 43). The remedy we adopt here is to model explicitly the generating process of ancestry tracts (e.g., a crossover model) and to integrate information across all markers in picking the best-fitting architecture.^†, ^‡

Polygenic traits are common in humans (44), and between-species traits such as hybrid incompatibilities can be more complex due to greater genomic divergence. However, the current analysis is limited by our backcross design, which forces ancestry tracts to be highly autocorrelated. In some cases, this limitation reduces the power to distinguish polygenicity from alternative architectures. For instance, pupal weight in B(BD) females can be explained either by a polygenic model with two jumps, or by two QTLs flanking the chromosome center. It is also possible that our relatively small sample sizes restricted the resolution of mapping. A more powerful test for polygenicity needs to generate random introgression on the Z chromosome with more configurations than available in this study. For Lepidoptera, species with more rapid reproduction and higher fecundity than our study systems are perhaps more suitable for this approach.

Polygenic Incompatibility Resembles Global Epistasis.

Hybrid incompatibility is usually perceived as negative epistasis between species-specific mutations (33, 35). While our phenomenological explanation invokes epistasis, the interaction may effectively be between ancestry fractions on different chromosomes. This is similar to “global epistasis,” where the phenotypic effect of a genetic change is somewhat independent of specific loci underlying the change (45). Global epistasis can emerge as transformations of additive components (e.g., the function $g$ on $f_Z$) and has been found previously in incompatibility. For instance, hybrid male sterility in Drosophila develops when the total introgressed ancestry surpasses a threshold, but it is insensitive to precise introgressed regions (46–48).

Conclusion

When we embarked on these studies of butterfly hybrid incompatibilities, we hoped to locate key genes causing defects. Surprisingly, it seems clear instead that sterility and other incompatibilities are often polygenic and that this polygenicity can provide simple explanations for some hitherto mysterious rules of hybrid incompatibility.

Materials and Methods

Breeding.

Lineages of P. dehaanii were purchased directly from a butterfly farm in Qingdao (Shandong Province, China), exclusively sourced from a small local population. Lineages of P. bianor were collected in the field from Ningbo (Zhejiang Province, China) for breeding in 2020 and 2021. A few individuals were also collected in the field from Kunming (Yunnan Province, China) for breeding in 2019. All crosses were done by hand-pairing. Eggs were collected by putting females in small cages with host plants under fluorescent light. The following host plants were used throughout the project: Tetradium daniellii, Zanthoxylum bungeanum, Z. ailanthoides, Z. beecheyanum, Z. simulans, Choisya ternata, and Phellodendron amurense. Larvae and pupae were kept in greenhouse conditions (approximately 20 ${}^{°}$C–35 ${}^{°}$C), with a combination of natural and greenhouse lights to maintain at least 10 h of illumination per day. Adults for dissection were immediately put into a 5 ${}^{°}$C room after eclosion to reduce activity. Otherwise, they were fed with sugar water once a day, and females were subsequently kept in the dark, while males were in an illuminated growth chamber to facilitate hand-pairing.

Phenotyping Ovaries.

Ovaries were dissected from females within five days of eclosion in 1× PBS solution. Ovariole sheath was manually removed, and most images were taken using the internal camera of a Leica EZ4 HD stereo microscope (pictures of a few specimens were taken by a cellphone through the eyepiece of a Zeiss Stemi 2000 stereo microscope). Due to a limitation of the stereoscope, many stereoscope images were not scaled exactly at the time of image acquisition. The approximate scales of these images were determined by comparing magnification levels against images with predetermined scales. This level of inaccuracy does not affect phenotypic scores because only qualitative differences (i.e., ovariole shapes and the presence/absence of certain structures) were used to classify phenotypes. Since ovary phenotypes are categorical, we established all major categories by defining the most obvious and the most frequent phenotypes across all dissected ovaries. These categories were confirmed later by confocal imaging that they have significant qualitative differences (Fig. 2). Phenotype Jammed is variable in terms of the fraction and the position of Jammed follicles. We lumped variable forms of Jammed into a single category in QTL analyses to reduce human bias in separating different kinds of Jammed.

A small number of ovaries have ambiguous phenotypes for one of the following reasons: 1) Different ovarioles develop different phenotypes; 2) some part of the ovary is lost in dissection; and 3) extremely rare phenotypes resembling none of the existing categories. These ambiguous individuals, mostly from D(DB) females, were assigned multiple categories. When such uncertainty affects analyses, two methods were used: 1) For simultaneous analysis of more than two ovary phenotypes, randomly select a phenotype from previously assigned categories on ambiguous individuals, perform analyses, and repeat the same procedure many times; 2) for QTL mapping in software r/qtl or r/qtl2 with binary categorical traits, map QTLs with ambiguous individuals scored as 0 (and 1) in the first (and the second) attempt.

Staining and Confocal Imaging of Ovaries.

Dissected ovaries were fixed in 4% Paraformaldehyde solution in 1× PBS for 20 min at room temperature. The ovaries were washed for 15 min each in 0.1% PBTx (1× PBS, 0.1% Triton-X 100), 1% PBTx, 2% PBTx, 0.01% Saponin (Sigma Aldrich 47036) in 1× PBS and Blocking solution (1X PBS, 0.3% Triton-X 100, 0.5% Normal Goat Serum). The ovaries were then stained for 12 h using the following reagents at 1:500 dilution in blocking solution: Hoechst 33342 (10 mg/mL, Thermo Fisher H3570), Wheat Germ Agglutinin-647 (WGA, Thermo Fisher W32466), and Rhodamine Phalloidin (Thermo Fisher R415). Stained ovaries were washed four times for 15 min each in 0.1% PBTx followed by a final 1× PBS wash. After the washes, ovaries were mounted in equal volumes of 1× PBS and Vectashield mountant (Vector labs H1900) on a slide.

The ovary samples were imaged by acquiring Z-section images on a Zeiss LSM 880 laser scanning confocal microscope at Harvard Center for Biological Imaging. The microscope was equipped with an Argon laser and a He/Ne 633-nm laser. Zeiss Plan-Apochromat 10×/0.45 M27 or 20×/0.8 M27 objective lenses were used for imaging. All images were 1024 × 1024 pixels in size and were acquired using PMT detectors. Images were acquired at excitation/emission wavelengths of 405/450 nm for Hoechst 33342, 561/610 nm for Rhodamine Phalloidin, and 633/696 nm for WGA.

DNA Extraction and Sequencing.

Samples from the cross were preserved in either pure ethanol or RNAlater at $-$20 ${}^{°}$C prior to DNA extraction. For extraction, we used E.Z.N.A Tissue DNA kits (Omega Bio-tek, Inc.). Whole-genome library preparation was performed using Illumina DNA 1/4 reaction kits at Harvard University Bauer Core, barcoded, and subsequently sequenced altogether on a single lane of Illumina NovaSeq S4. Autosomal coverage varies among individuals: backcrosses—1×, F₁s-5×, parents—30× to 60×. Raw reads were trimmed with Cutadapt-3.4 (49) to remove adapters (CTGTCTCTTATACACATCT), and subsequently mapped to the reference genome of P. bianor using the BWA-0.7.17 MEM algorithm. Duplicate reads were marked using Picard-2.25.7 (50). We used BCFtools-1.9 (51) to pile up reads with very light quality filtering and called variants with associated genotype likelihoods. VCF files produced by the variants caller were used for linkage analysis.

Linkage Analysis.

For quality control, we first calculated kinship coefficients among individuals using NgsRelate-2 (52) and corrected the pedigree position of a few individuals (SI Appendix, Fig. S3). Lep-MAP-3 was used for all subsequent linkage analysis (53). First, VCF files and the pedigree were combined in module ParentCall2, and we imputed haplotype structure along the reference genome with module OrderMarkers2. We also generated de novo marker orders using the same module. Comparing de novo marker orders against the order in the original reference genome revealed some intra-chromosome assembly problems. We corrected these problems below.

Linkage-based Reference Genome Correction.

For a precorrection reference genome (31), we plotted the de novo marker order against the genomic order. We found some reference assembly errors that affect the order and orientation among PacBio scaffolds on chromosomes. Using inferred haplotypes in the “grandparental” phase (i.e., the parents from the cross. This terminology “grandparental phase” is used in Lep-MAP-3), we calculated the correlation of ancestry between each pair of markers, which should be a decreasing function of marker distance on each chromosome due to recombination. This information enabled us to correct large-scale errors, and an intermediate reference genome was generated. To correct smaller errors, we inferred de novo marker order by Lep-MAP-3 on the intermediate genome and compared it against the intermediate genome. This extra step corrected the position/orientation of several smaller scaffolds. We were able to correct all errors identified in this way except for those on chromosome 14, where an apparent orientation problem appears to occur within a PacBio scaffold, and we were unable to determine its breakpoint. (This may be due to a different population used here compared to the reference population). The de novo marker order inferred from this final genome is mostly collinear to the genomic order (SI Appendix, Fig. S4), confirming that most visible errors in concatenating scaffolds have been eliminated. Finally, haplotypes in the grandparent phase were reinferred using the corrected reference genome for all subsequent analyses.

Inferring Crossover Frequency.

To infer crossover frequency, we counted the number of recombination breakpoints in each paternal haplotype among all backcross individuals (For all paternal haplotypes, see SI Appendix, Figs. S5–S7). No chromosome has more than two breakpoints except for chromosome 14 (likely due to the aforementioned reference error). We excluded chromosome 14 from this crossover analysis. Let $n_0$, $n_1$, and $n_2$ be the number of haplotypes having 0, 1, or 2 recombination breakpoints for a given chromosome. The maximum likelihood estimate of crossover frequency is as follows (see “SI Appendix, section 1” for derivation). First, calculate

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill c_0& =(n_0-n_1+n_2)/(n_0+n_1+n_2)\hfill \\ \hfill c_1& =(2n_1-4n_2)/(n_0+n_1+n_2)\hfill \\ \hfill c_2& =4n_2/(n_0+n_1+n_2).\hfill \end{array}\end{array}$$ [1]

If $c_0,c_1,c_2$ are all nonnegative, they are the inferred frequencies of having 0, 1, or 2 crossovers. If $c_0<0$, the adjusted estimate is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill c_0^{\ast }& =0\hfill \\ \hfill c_1^{\ast }& =(n_0-n_2)/(n_0+n_2)\hfill \\ \hfill c_2^{\ast }& =2n_2/(n_0+n_2).\hfill \end{array}\end{array}$$ [2]

QTL Scans by Marker Regression in r/qtl and r/qtl2.

One-dimensional QTL scans were performed with R-package qtl2 (43), and two-dimensional scans were performed with R-package qtl (42). To calculate LOD scores, ovary phenotypes were always mapped one at a time using a binary trait logistic mapper (i.e., phenotype of interest = 1; other phenotypes = 0). This approach is suitable for unordered categorical traits such as ovary morphology. For pupal weight, we introduced brood as a covariate to control for seasonal variation in pupal weight due to diet and environmental factors. LOD score thresholds were always estimated on 1,000 random permutations of phenotypes. To compute $R^2$ when comparing the polygenic model of ovary dysgenesis with observed results, we did not use a logistic mapper. Instead, we coded “Normal” as 1 and all other phenotypes as 0 and then performed regression directly on marker ancestry.

Bayesian QTL Model Selection.

We used the software BayesQTLBIC-1.0-2 (32) to evaluate the posterior probabilities of alternative QTL models. This algorithm assumes additivity among markers. Although the software is extendable to epistasis between markers, the large number of alternative models for epistasis forbids enumerating across all of them. Also, based on the software manual, the prior for epistasis coefficients is not intuitive to define, while the prior for additive effects is well defined and was set at $0.5$ (uniform prior). This limits our implementation of this software to the analysis of only pupal weight. In pupal weight analysis, we chose 15 sparsely spaced markers on the Z chromosome. This complexity allows us to loop over many models up to six QTLs. The parameters used in the R code is

result $<$$-$ bicreg.qtl(x $=$ genotype, y $=$ phenotype, maxCol $=$ 41, OR $=$ 1000000000, nbest $=$ 500, nvmax $=$ 6, prior $=$ 0.5, keep.size $=$ 1).

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Raw reads are released in the NCBI Sequence Read Archive (BioProject: PRJNA892033). Source data and code for main and supplementary figures are deposited in Zenodo (https://doi.org/10.5281/zenodo.7229625) (54). Source code (independent copy) is also available from https://github.com/tzxiong/2022_Papilio_HybridIncompatibilityMapping (55). Previously published data were used for this work (26, 31).