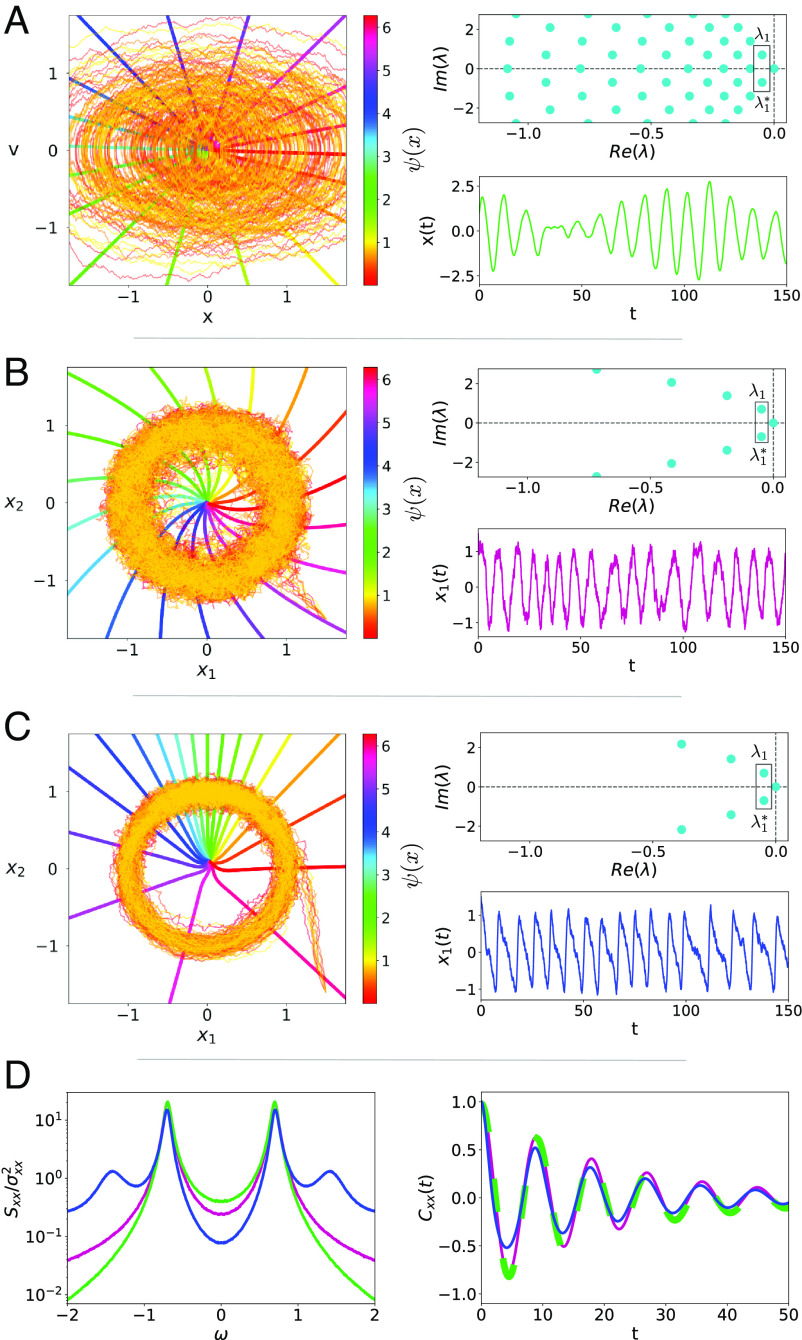
Fig. 1.

Three models of “robust” stochastic oscillations. In the three panels, we show for each model ten sample trajectories in phase space together with the stochastic asymptotic phase ψ(x) (Left), a time series of one of the components (Lower Right), and the spectrum of eigenvalues (Top Right). For the three models, parameters have been tuned so they have the same value for the eigenvalue λ₁ = −0.048 + 0.698i with the smallest nonvanishing real part. (A) Damped noisy harmonic oscillator for M = 1, γ = 0.096, ω₀ = 0.699, D = 0.01125. (B) Noisy Stuart–Landau for a = 1, b = −0.3, D₁ = D₂ = 0.04. (C) Noisy SNIC model (beyond the bifurcation, i.e., in the limit-cycle regime) for m = 1.216, n = 1.014, and D₁ = D₂ = 0.0119. (D) Power spectra (Left) and correlation function (Right) of x(t) (harmonic oscillator, green), x₁(t) (noisy Stuart–Landau model, purple), and x₁(t) (SNIC model, blue).