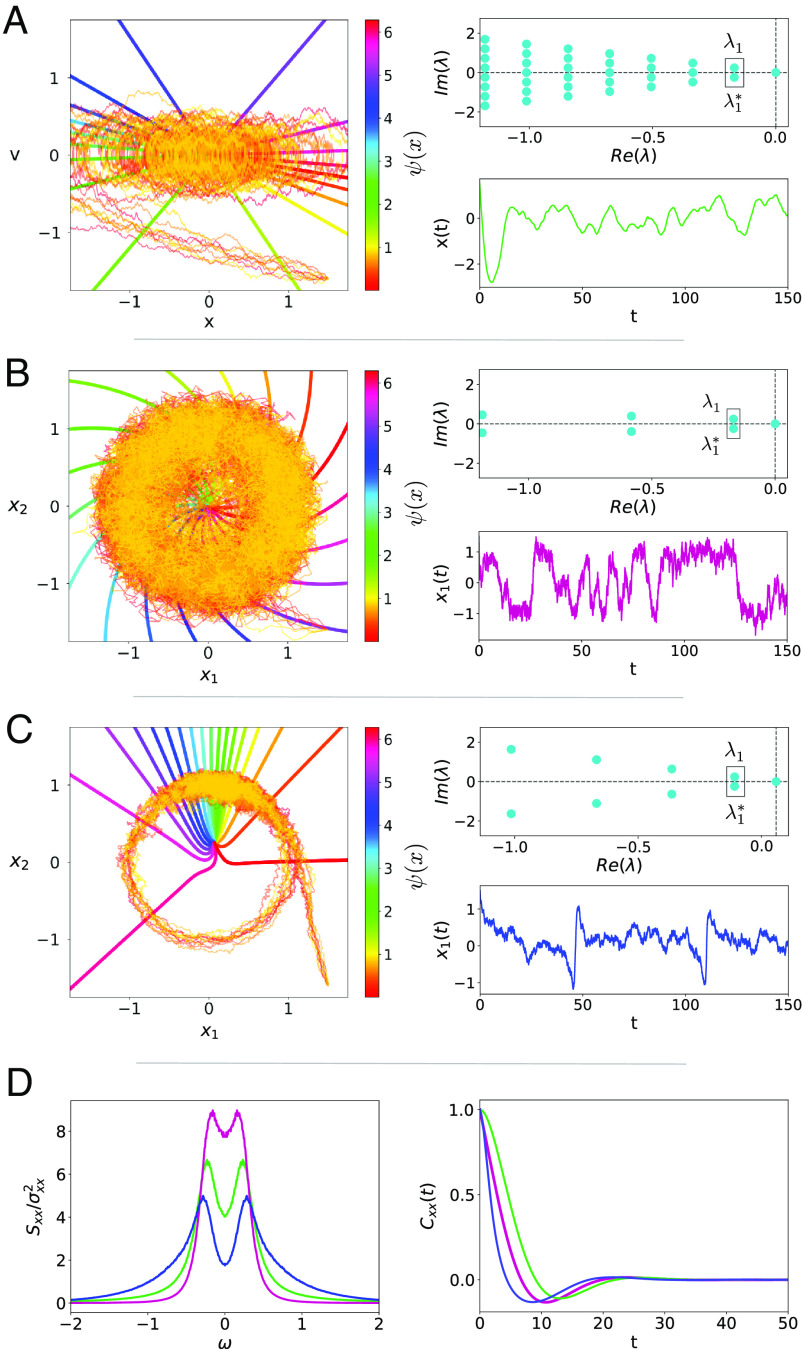
Fig. 2.

Three models of stochastic oscillations. In the three panels, we show for each model ten sample trajectories in phase space together with the stochastic asymptotic phase ψ(x) (Left), a time series of one of the components (Lower Right), and the spectrum of eigenvalues (Top Right). For the three models, parameters have been tuned, so they have the same value for slowest decaying eigenvalue λ₁ = −0.168 + 0.241i. (A) Damped noisy harmonic oscillator for M = 1, γ = 0.337, ω₀ = 0.294, D = 0.01125. (B) Noisy Stuart–Landau for a = 1, b = −0.713, and D₁ = D₂ = 0.0995. (C) Noisy SNIC model (prior to the bifurcation, i.e., in the excitable regime) for m = 0.99, n = 1, and D₁ = D₂ = 0.01125. (D) Power spectra (Left) and correlation function (Right) of x(t) (harmonic oscillator, green), x₁(t) (noisy Stuart–Landau model, purple), and x₁(t) (excitable SNIC model, blue).