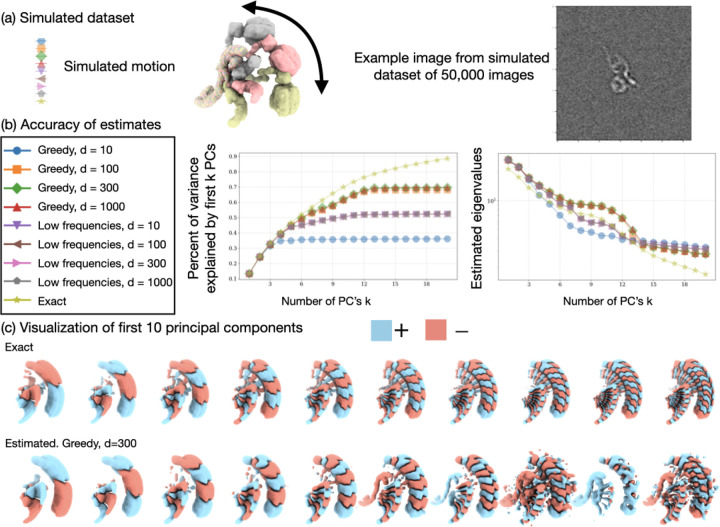
Figure A.6:

Accuracy of the proposed PCA method on a synthetic dataset. (a) Simulated dataset: a synthetic motion described in [65], and a synthetic dataset of 50,000 images. (b) Accuracy of principal components and estimated eigenvalues for different parameters. We compare the accuracy of two column sampling strategies: “Greedy” is the one described in appendix A.2, and “Low frequencies” is picking the columns corresponding to the lowest frequency voxels. We also show accuracy from computing a different number of columns $d=\mathrm{10,100,300,1000}$ (before doubling using the Hermitian symmetry). The accuracy of the principal component is described using percent of the captured variance, computed as ${‖{\left(U_k^{*}\Sigma U_k\right)}^{1/2}‖}_F^2/{‖{\Sigma }^{1/2}‖}_F^2$, where $U_k$ is the matrix containing the first $k$ estimated principal components, $\Sigma$ is the true covariance matrix and ${\Sigma }^{1/2}$ is the matrix square-root, so that ${‖A^{1/2}‖}_F^2={\sum }_i{\sigma }_i\left(A\right)$ where ${\sigma }_i\left(A\right)$ are the singular values of $A$. Thus, the first 20 exact principal components capture 90% of the variance (which is the optimal choice), whereas the estimated using (Greedy, $d=300$) captures around 70% of the captured variance. Here, the “Low frequency” sampling scheme achieves similar performance for all values of $d$ (around 50% of captured variance), and the “Greedy” scheme improves with $d$ until around $d=100$ (around $70\%$ of captured variance). The default value in RECOVAR is $d=300$, which we observed empirically to be robust to a wide range of distributions. The scheme slightly overestimates the eigenvalues by a factor of around 1.2, possibly due to a misestimation of the mean and noise distribution which inflates the covariance estimate. Nevertheless, the decay of eigenvalues is correctly estimated until around the 12 th eigenvalue where the noise dominates. (c) Visualization of the first ten exact and estimated principal components. The exact principal components are increasing in frequency, oscillating between positive and negative in the direction of motion. The estimated principal components increase in frequency but are increasingly noisy.