Abstract

Quantum computers are capable of calculating the energy difference of two electronic states using the quantum phase difference estimation (QPDE) algorithm. The Bayesian inference-based implementations for the QPDE have been reported so far, but in this approach, the quality of the calculated energy difference depends on the input wave functions being used. Here, we report the inverse quantum Fourier transformation-based QPDE with Na of ancillary qubits, which allows us to compute the difference of eigenenergies based on the single-shot projective measurement. As proof-of-concept demonstrations, we report numerical experiments for the singlet–triplet energy difference of the hydrogen molecule and the vertical excitation energies of halogen-substituted methylenes (CHF, CHCl, CF2, CFCl, and CCl2) and formaldehyde (HCHO).
1. Introduction
Quantum computing is one of the most innovative research fields in current science and is anticipated to bring breakthroughs in quantum chemical calculations. Quantum chemical calculations are based on the Schrödinger equation, which governs the dynamics of quantum particles, and accurate quantum chemical calculations can potentially open the door to predictive quantum chemistry. However, as Dirac noted, “The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble”.1 The computational cost of the full configuration interaction (full-CI) method, which is the variationally best possible wave function in the Hilbert space spanned by the basis set used, scales exponentially with system size, and it is impractical except for small molecules with a medium-size basis set.
Since quantum chemical calculations deal with the dynamics of electrons in atoms and molecules, it is a potentially amenable problem for quantum computers. In fact, in 2005, Aspuru-Guzik and coworkers reported a method for performing the full-CI calculation on a quantum computer,2 using a quantum phase estimation (QPE) algorithm.3–5 The QPE is a quantum algorithm that is capable of computing the eigenvalues and corresponding eigenvectors of a unitary operator U. By using the time evolution operator exp(−iHt) for U, one can calculate the full-CI energies on a quantum computer. However, because QPE utilizes the projective measurement of the quantum state to obtain the eigenfunction and the corresponding eigenvalue, it is probabilistic, and which electronic state is obtained from the QPE depends on the overlap between the approximate wave function used as the input and the exact eigenfunction. Importantly, the QPE itself does not guarantee an exponential speedup of quantum chemical calculations,6 and connecting theoretical methods to generate sophisticated approximated wave function is necessary.
Quantum chemical calculations can afford to compute the total energies of atoms and molecules, but total energies are generally not available from experiments. Chemical phenomena relevant to quantum chemical calculations are usually discussed in terms of the energy differences between different geometries or electronic states. Thus, an accurate prediction of the energy differences is crucial for the practical use of quantum chemical calculations in chemistry research and development.
Because quantum computers can use quantum superposition states as computational resources, it is possible to compute the energy differences directly on a quantum computer. In fact, several quantum algorithms for the direct estimation of energy differences have been reported, such as the quantum annealing-based approach,7 the quantum–classical hybrid algorithm,8 using the robust phase estimation technique,9 and the algorithms for fault-tolerant quantum computers including the Bayesian exchange coupling parameter calculator with broken-symmetry wave functions (BxB) algorithm10 and the Bayesian phase difference estimation (BPDE) algorithm.11–14 In addition to these methods, multiple eigenvalue estimation techniques for the simultaneous determination of the ground and the excited-state energies have been reported.15–17 In particular, the BPDE algorithm reported by us is an extension of the Bayesian phase estimation (BPE)18–20 to the quantum phase difference estimation using the quantum superposition of two electronic states. BPDE is in principle applicable to arbitrary electronic states, and it is free from the controlled-time evolution requited in conventional QPE algorithms for total energy calculations. The BPDE algorithm has been applied to the direct calculation of ionization energies, singlet–triplet energy differences and valence excitation energies,11 total energies by using the quantum superposition of the desired electronic state and the vacuum state,12 finite difference-based numerical energy gradients,13 and relativistic energy differences (fine structure splitting).14 The BPDE algorithm is a powerful tool for studying the energy difference of atoms and molecules, but it has two major weaknesses. (1) It requires many circuit executions to compute the energy differences, and the calculated energy differences suffer from shot noise; and (2) it is not projective, and the calculated energy difference depends on the approximated wave functions used as the input. The second drawback can be clearly seen in the total energy calculations of the transition state between trans and iso isomers of the N2H2 molecule.12 It is desirable to extend the quantum phase difference estimation (QPDE) algorithm to projective measurement-based methods.
In this work, we propose a projective measurement-based QPDE algorithm with the Na of ancillary qubits. Hereafter, we denote the proposed approach as the “N-qubit QPDE” algorithm. The N-qubit QPDE is a natural extension of the N-qubit QPE to the phase difference estimation, and it can compute the eigenenergy difference even if we use approximated wave functions as inputs. Similar to the N-qubit QPE for total energy calculations, which eigenenergy difference is obtained in the N-qubit QPDE depends on the overlap between the approximated wave functions and the eigenfunctions. To our knowledge, all other approaches for the direct calculation of the energy difference reported so far are neither projective nor single-shot protocols, and this is the first attempt to perform the eigenenergy difference calculation on a quantum computer without repetitive quantum circuit executions. As the demonstrations, we report numerical quantum circuit simulations for the singlet–triplet energy difference of the H2 molecule and the vertical excitation energies of halogen-substituted methylenes (CHF, CHCl, CF2, CFCl, and CCl2) and formaldehyde (HCHO). We also report the application of an algorithmic error mitigation (AEM)21 to remove the Trotter–Suzuki decomposition error and to improve the calculated energy differences.
2. Theory
First, we briefly discuss the BPE18–20 and the BPDE11 algorithms. The quantum circuits for the BPE and the BPDE algorithms are shown in Figure 1. Here, H is an Hadamard gate, Pr(g) is an approximate ground state preparation gate defined in eq 1, U is a time evolution operator given in eq 2, P is a phase shift gate defined in eq 3, Ex is a quantum circuit that generates an approximated excited-state wave function |Φ1⟩ from the approximated ground-state wave function |Φ0⟩ as in eq 4, and ε and Δε are estimators of the total energy and the energy difference, respectively. Throughout this paper, we have used {|Φ⟩} for approximated wave functions and {|Ψ⟩} for eigenfunctions. Ns in eq 1 is the number of qubits used to store the wave functions. In conventional fermion–qubit mapping methods such as the Jordan–Wigner transformation (JWT)22 and the Bravyi–Kitaev transformation (BKT),23Ns is equal to the number of spin orbitals included in the active space. Roughly speaking, QPDE can be implemented by replacing the controlled-time evolution operation in QPE by controlled-excitation and subsequent time evolution and controlled-deexcitation operations.
| 1 |
| 2 |
| 3 |
| 4 |
Figure 1.
Quantum circuits for (a) BPE and (b) BPDE algorithms. The definition of quantum gates is given in the main text.
By expanding the approximated wave functions by eigenfunctions as given in the right side of eqs 1 and 4, the probability of obtaining the |0⟩ state in the measurement of an ancillary qubit, Prob(0), can be calculated as in eqs 5 and 6 for the BPE and the BPDE, respectively.
| 5 |
| 6 |
These equations insist that if the approximated wave functions |Φ⟩ have sufficiently large overlaps with the eigenfunctions of the target electronic states, then Prob(0) becomes maximum at ε = Ej and Δε = ΔEjk for the BPE and the BPDE, respectively. In the BPE and the BPDE algorithms, total energies and energy differences are computed by searching for the ε and Δε, respectively, values that give maximum Prob(0), using Bayesian inference.
From eqs 5 and 6, it is clear that the accuracy of the calculated total energies and energy differences in the framework of the BPE and the BPDE algorithms strongly depends on the quality of the approximated wave functions being used as the inputs. If the approximated wave functions are expressed by linear combinations of many eigenstates and contributions from electronic states other than the target state to Prob(0) become non-negligible, then the peak position of Prob(0) may be shifted from that corresponding to the true eigenvalues. For typical closed-shell singlet molecules in their equilibrium geometries, the Hartree–Fock wave function |ΦHF⟩ is a reasonably good approximation of the ground-state wave function. However, the overlap squared value |⟨ΦHF|Ψfull–CI⟩|2 can decrease exponentially with the system size, and therefore using |ΦHF⟩ as the input wave function is only valid for small molecules. One possible solution is to adopt an adiabatic state preparation (ASP) algorithm to generate correlated wave functions.2,24–26 However, the quantum circuit for the ASP is usually deep, and it is unsuitable for the BPE and BPDE frameworks which need repetitive quantum circuit executions.
In the total energy calculations, single-shot projective calculations are possible by using the QPE algorithm with Na of ancillary qubits.2 The quantum circuit for the N-qubit QPE is shown in Figure 2a. Here, QFT† represents the quantum circuit for the inverse quantum Fourier transformation.27 By assuming eq 1, the quantum state before the measurement of ancillary qubits in Figure 2a is calculated as in eq 7.
| 7 |
Figure 2.
Quantum circuits for (a) N-qubit QPE algorithm, (b) N-qubit QPDE algorithm in a naive implementation, and (c) N-qubit QPDE algorithm used in this work.
Thus, the measurement of ancillary qubits yields an eigenphase ϕj = 0.x1x2x3...xNs in binary fraction with the probability proportional to |cj|2, and the wave function is projected onto the corresponding eigenfunction |Ψj⟩. Here, xk is the measurement outcome of the k-th ancillary qubit. The eigenenergy E can be calculated by using the equation E = −2πϕ/t, which is derived from the equation e–iHt|Ψ⟩ = e–iEt|Ψ⟩ = e2iπϕ|Ψ⟩. From an analogy of the extension of the BPE algorithm to the BPDE, we can construct the quantum circuit for the N-qubit QPDE algorithm by replacing the controlled-U gates with the sequence of controlled-Ex, U, and controlled-Ex† gates, as in Figure 2b. Note that the quantum circuit in Figure 2b contains control-free time evolution operations, and therefore, this implementation implies that |Φ0⟩ is an eigenfunction of the time evolution operator. Unfortunately, this assumption is not generally true. This difficulty can be avoided by starting from the |0⟩⊗Ns state and using the controlled-Pr gate given in eq 8 instead of using the controlled-Ex gate, as shown in Figure 2c.
| 8 |
Here, Pr(g)|0⟩⊗Ns = |Φ0⟩ and Pr(e)|0⟩⊗Ns = |Φ1⟩. Since the |0⟩⊗Ns state in JWT and BKT corresponds to the vacuum state with no electrons, applying U does not change the state U|0⟩⊗Ns = |0⟩⊗Ns. As a result, the quantum circuit for the N-qubit QPDE is slightly deeper than that for the N-qubit QPE. In the present study, the approximated wave functions are expressed by a linear combination of at most two Slater determinants, and thus, the quantum circuits for controlled-Pr are sufficiently shallow. Note that in the present study we have focused on the energy difference of two electronic states at the same molecular geometry, but it is possible to extend the algorithm for the direct calculation of the energy differences of different molecular structures. This can be accomplished by using the time evolution operator conditional on the ancillary qubit (|0⟩⟨0|⊗e–iHAt + |1⟩⟨1|⊗e–iHBt) instead of the control-free time evolution operator, where HA and HB are Hamiltonians at geometries A and B, respectively. If HA and HB share the same Pauli strings, such a conditional time evolution operation can be implemented by slightly increasing the proportionality factor of the gate count scaling without increasing the scaling of the gate count from the original QPE algorithm by using the technique developed in the BPDE-based numerical energy gradient calculations.13
In the implementation described in Figure 2c, the bit string obtained from the measurement of ancillary qubits corresponds to the eigenphase difference Δϕjk = 0.x1x2x3...xNs, and the eigenenergy difference can be calculated as ΔEjk = −2πΔϕjk/t. The probability by which the eigenenergy difference is obtained is proportional to |cj|2 × |dk|2. Although the overall probability of success in calculating the target energy difference is the same between two separate total energy calculations by the N-qubit QPE and the direct calculation of the energy difference by the N-qubit QPDE, the identification of the target energy difference may be more difficult for the N-qubit QPDE when the quality of the approximated wave functions is not so high. In the case of the total energy calculations, one can determine the ground-state energy based on the variational principle by comparing the obtained energies. In the case of energy difference calculations, however, such an evaluation is not possible. In this context, sophisticated state preparation is more important in the N-qubit QPDE algorithm. Nevertheless, the N-qubit QPDE-based direct calculation of the energy difference has two advantages over the putative approach based on the N-qubit QPE for total energy calculations of individual electronic states: (1) It is free from controlled-time evolution operations, and (2) the number of ancillary qubits can be smaller than in total energy calculations. The latter feature is due to the fact that the energy difference to be discussed is much smaller than the total energy itself. Since the number of ancillary qubits is equal to the number of binary digits of the phase to be determined, molecules with large absolute energies require more qubits.
It should be noted that the energy difference
can be positive or
negative, but the Δϕjk obtained
from the N-qubit QPDE quantum circuit does not contain
information about the digits above the arithmetic point. Therefore,
Δϕjk and Δϕjk – k, where k is an arbitrary integer, cannot be distinguished in the N-qubit QPDE. This means that there is a possibility to
assign a wrong sign to the energy difference. To avoid such a misassignment,
we can appropriately set the evolution time length t so that cos(2πΔϕjk) > 0, and use Δϕjk when
0 ≤ Δϕjk ≤ 1/4
and Δϕjk – 1 when 3/4
≤ Δϕjk < 1. If the
eigenphase difference Δϕjk is calculated between 1/4 and 3/4, we cannot immediately determine
the sign of the energy difference. However, even in this case, we
can determine the sign by performing another N-qubit
QPDE calculation by adding the phase shift gate P(ΔEljk) just after time
evolution operator Ul. This can be understood as follows: When the time evolution operator U is applied to the quantum superposition state  , the quantum state transforms to
, the quantum state transforms to  , where ΔE01 = E1 – E0. The subsequent application of the phase shift gate results
in the quantum state
, where ΔE01 = E1 – E0. The subsequent application of the phase shift gate results
in the quantum state 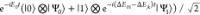 . Thus, if ΔEjk is positive, the N-qubit
QPDE with the phase shift gates returns Δϕ = 0, and in
the case when ΔEjk is negative, the N-qubit QPDE returns the phase
Δϕ = 2Δϕjk.
. Thus, if ΔEjk is positive, the N-qubit
QPDE with the phase shift gates returns Δϕ = 0, and in
the case when ΔEjk is negative, the N-qubit QPDE returns the phase
Δϕ = 2Δϕjk.
3. Computational Conditions
As proof-of-concept demonstrations of the proposed N-qubit QPDE algorithm, here we report numerical simulations for the direct calculation of the singlet–triplet energy difference of the H2 molecule and the vertical excitation energies of halogen-substituted methylenes (CHF, CHCl, CF2, CFCl, and CCl2) and formaldehyde (HCHO). We computed the singlet–triplet energy difference as the excitation energy of the spin-triplet state from the spin-singlet state. Because all of the molecules under study have the spin-singlet ground state, the singlet–triplet energy difference ΔEST = E(T1) – E(S0) is positive. Note that numerical simulations of the BxB and the BPDE-based energy difference calculations have been reported10,11 for some of the compounds under study. In our previous publications, the singlet–triplet energy difference of H2 was defined as ΔE = E(S0) – E(T1), and therefore, the definition of the energy difference is different. The one- and two-electron integrals required to construct the electronic Hamiltonian were computed by using the General Atomic and Molecular Electronic Structure System (GAMESS-US) program package.28 The full-CI and the complete active space configuration interaction (CAS-CI) calculations as the references were also performed with GAMESS-US. Numerical quantum circuit simulations were performed by using our in-house Python code developed with the OpenFermion29 and Cirq30 libraries.
The singlet–triplet energy difference of the H2 molecule with the atom–atom distance from 0.7 to 3.0 Å was studied by using the 6-31G basis set. The wave function is encoded in 8 qubits using JWT, and 12 ancillary qubits were used for the phase readout. The evolution time length in the U = exp(−iHt) operator was set to t = 10. We set the evolution time length t considerably long because the singlet–triplet energy difference of the H2 molecule is very small for long H–H distances. The second-order Trotter–Suzuki decomposition31,32 given in eq 9 was adopted to construct the quantum circuit. An error of the second-order Trotter decomposition scales quadratic against the time length of the single Trotter step Δt,33,34 which is very important to apply the AEM. We examined three different time lengths for the single Trotter steps: Δt = t/M = 0.5, 1.0, and 1.25.
| 9 |
Here, Pj is a Pauli string described by a direct product of Pauli operators {I, X, Y, Z}, ωj is the corresponding coefficient, and J is the number of Pauli strings included in Hamiltonian H. It is known that the Trotter–Suzuki decomposition error depends on the term ordering.35,36 In this study, we used a magnitude ordering35 where the Pauli string is applied in decreasing order of |ωj|.
As discussed in the previous section, the probability of which energy difference can be obtained is proportional to |cj|2 × |dk|2, where cj and dk are the coefficients defined in eqs 1 and 4, respectively. This means that the accuracy of the approximated wave functions only affects the success probability, and if success occurs, the energy difference obtained from the N-qubit QPDE does not depend on the quality of the wave functions. To study the input wave function dependence in a H2 molecule with the 6-31G basis set, we used two different wave functions for the ground-state spin-singlet wave functions. One is the Hartree–Fock wave function |ΦHF⟩, and the other is the two-configurational wave function |Φ2c⟩ constructed by using a diradical character y and the natural orbitals computed at the broken-symmetry spin-unrestricted Hartree–Fock (BS-UHF) level. As reported in our precedent paper,37 the |Φ2c⟩ defined as in eq 10 can be a qualitatively good approximated wave function of diradical systems with a large overlap with the full-CI wave function. The diradical character y was calculated from the occupation number of the lowest unoccupied natural orbital (nLUNO) constructed from the BS-UHF wave function for the MS = 0 state, as given in eq 11.38
| 10 |
| 11 |
Here, |2000⟩ is the Hartree–Fock
(HF)-like configuration  and |0200⟩ is the highest occupied
natural orbital (HONO)–lowest unoccupied natural orbital (LUNO)
two-electron excited determinant from the HF-like configuration in
the H2 molecule with the 6-31G basis set (4 molecular orbitals
and 2 electrons). The BS-UHF natural orbitals of H2 are
illustrated in Figure 3. For the spin-triplet state, we used the spin-restricted open-shell
Hartree–Fock (ROHF)-like configuration |Φ1⟩ = |αα00⟩, where α indicates that
the molecular orbital is singly occupied by a spin-α electron.
The controlled-Pr gates used for the calculations are depicted in Figure 3.
and |0200⟩ is the highest occupied
natural orbital (HONO)–lowest unoccupied natural orbital (LUNO)
two-electron excited determinant from the HF-like configuration in
the H2 molecule with the 6-31G basis set (4 molecular orbitals
and 2 electrons). The BS-UHF natural orbitals of H2 are
illustrated in Figure 3. For the spin-triplet state, we used the spin-restricted open-shell
Hartree–Fock (ROHF)-like configuration |Φ1⟩ = |αα00⟩, where α indicates that
the molecular orbital is singly occupied by a spin-α electron.
The controlled-Pr gates used for the calculations are depicted in Figure 3.
Figure 3.

Natural orbitals constructed
from the BS-UHF wave function and
the controlled-Pr gate used for the N-qubit QPDE
calculations of the H2 molecule. The rotation angle of
the Ry gate is set to
be 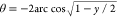 , where y is the diradical
character calculated using eq 11.
, where y is the diradical
character calculated using eq 11.
The numerical simulations of halogen-substituted methylenes were carried out at the CAS-CI/6-31G* level using the Becke, 3-parameter, Lee–Yang–Parr (B3LYP)/6-31G* optimized geometry. Geometry optimizations were performed using Gaussian 09 software.39 Cartesian coordinates of the optimized geometries are summarized in the Supporting Information. We used the (6e, 4o) active space for CHF and CHCl and the (10e, 6o) active space for CF2, CFCl, and CCl2, and the vertical excitation energies of the lowest spin-triplet excited state (13B1 state) were calculated. Here, (ke, lo) specifies that the active space contains k-electrons and l-molecular orbitals. All the active spaces are given as Figures S1–S5 in the Supporting Information. We used ten ancillary qubits for the phase readout, and the evolution time length was set to be t = 10. The restricted Hartree–Fock (RHF) and ROHF-like single determinant wave functions were used for |Φ0⟩ and |Φ1⟩, respectively, and the quantum circuit similar to Figure 3 with θ = 0 is used for the controlled-Pr gate.
For direct calculations of the vertical excitation energies of formaldehyde (HCHO), we focused on the three low-lying excited states (11A2, 11B1, and 21A1 states). We used the same geometry and active space as our previous publication.11 The CAS-CI active space consists of 5a1 (C–O σ), 1b1 (C–O π), 2b2 (in-plane 2p lone pair of O), 2b1 (C–O π*), and 9a1 (C–O σ*) orbitals, as illustrated in Figure S6 in the Supporting Information. The excited-state wave functions are approximated by the spin symmetry-adapted (2b2 → 2b1), (5a1 → 2b1), and (1b1 → 2b1) one-electron excitations from the |ΦHF⟩ for the 11A2, 11B1, and 21A1 states, respectively. The quantum circuits of the controlled-Pr gates are illustrated in Figure S7 in the Supporting Information. The simulations were carried out using ten ancillary qubits and t = 10.
4. Results and Discussion
4.1. Effect of Input Wave Function in H2 Molecule
First, we checked the effect of the approximated wave functions on the success probability of the N-qubit QPDE and the calculated eigenphase difference value, by using |ΦHF⟩ and |Φ2c⟩ as the input wave functions for the spin-singlet electronic ground state of the H2 molecule. We used two different geometries R(H–H) = 2.0 and 3.0 Å as the representative examples of intermediate bond-breaking and bond-dissociation regions, respectively. The ground-state wave function exhibits a sizable diradical character [y = 0.4398 and 0.8648 for R(H–H) = 2.0 and 3.0 Å, respectively], and therefore |Φ2c⟩ is a much better approximation for the ground-state wave function than |ΦHF⟩.
Figure 4 summarizes the relationship between the phase value obtained from the measurement of the ancillary qubits and the probability of occurrence. The plots have two major peaks when |ΦHF⟩ is used as the input wave function for the singlet ground state. By converting the phase values of the peaks at the geometry R(H–H) = 2.0 Å to the energy unit, we obtained the energy differences as 0.027305 and −0.363553 hartree for the major and minor peaks, respectively. These values correspond to the (T1 – S0) and (T1 – S2) energy differences [ΔE(full-CI/6-31G) = 0.027980 and −0.361740 hartree, respectively]. Importantly, the difference in the input wave functions only affects the success probability, and the phase value giving a peak remains unchanged. These results support the projective nature of the N-qubit QPDE algorithm.
Figure 4.
Phase value vs probability plot obtained from the N-qubit QPDE simulations of H2 molecules with different input wave functions for the S0 ground state.
To check the consistency of the calculated energy differences when summed, we performed additional simulations for the direct calculation of the (S2–S0) excitation energy. The (S2–S0) energy difference calculated directly from the N-qubit QPDE is 0.390858 hartree, which is identical to the (T1–S0) – (T1–S2) value.
4.2. Singlet–Triplet Energy Difference of H2 Molecule with Different Bond Lengths and Application of the Algorithmic Error Mitigation
Next, we carried out the N-qubit QPDE simulations for the direct calculation of the singlet–triplet energy difference of the H2 molecule by changing the atom–atom distance from 0.7 to 3.0 Å. The calculated energy differences are plotted in Figure 5a and the deviations from the full-CI/6-31G energy difference are given in Figure 5b. Here, we used |Φ2c⟩ as the input wave function of the spin-singlet state, and the phase value giving the maximum measurement probability was taken as the eigenphase. From Figure 5, it is clear that the deviation from the full-CI value becomes smaller when a shorter time length is adopted for the single Trotter step. For the geometry with longer R(H–H) distances, the N-qubit QPDE simulations with t/M = 1.00 and 1.25 gave negative ΔE values (see the inset of Figure 5a), which are in contradiction with the full-CI/6-31G results.
Figure 5.

N-qubit QPDE simulation results of the H2 molecule with different time lengths of the single Trotter step t/M. (a) Singlet–triplet energy difference. Inset is the plot of ΔE at the geometry R(H–H) ≥ 2.5 Å. (b) Differences between the singlet–triplet energy differences from the quantum circuit simulations and from the full-CI/6-31G calculations. AEM stands for the energy difference calculated by using the algorithmic error mitigation technique (see text).
The plot in Figure 5b indicates that the ΔE values obtained from the N-qubit QPDE simulations have systematic errors. We assume that the main source of the errors is the Trotter–Suzuki decomposition. Apart from the Trotter–Suzuki decomposition error, a rounding error of the phase value due to the finite number of ancillary qubits can affect the ΔE values. Theoretically, using a shorter time length for the single Trotter step can systematically reduce the error, but there is a trade-off between the Trotter–Suzuki decomposition error and the computational cost. Instead of using a shorter time length for the single Trotter step, here we examined the AEM method.21 The AEM is a technique for mitigating errors of algorithmic origin such as the Trotter–Suzuki decomposition. It is known that the error in the second-order Trotter–Suzuki decomposition scales as O((Δt)2),33,34 as given in eq 9. Since we have fixed the evolution time length t for different Δt = t/M simulations, the energy difference including the Trotter–Suzuki decomposition error can be fitted by a quadratic function, f(Δt) = a(Δt)2 + b, where f(Δt) is the energy difference obtained from the N-qubit QPDE simulation with the single Trotter step size t/M = Δt. The residue b of the fitted function corresponds to the energy difference of the Trotter–Suzuki decomposition error zero limit estimated from the extrapolation. The results of the AEM are also plotted in Figure 5b (purple stars). It is clear that the AEM efficiently reduces the error in the energy difference estimation. In the case of the H2 molecule, the maximum value of |ΔE (AEM) – ΔE (full – CI)| is 0.00101 hartree = 0.633 kcal mol–1, which is below the chemical precision (1.0 kcal mol–1).
4.3. Vertical Lowest-Triplet Excitation Energies of Halogen-Substituted Methylenes
Next, we focused on the vertical excitation energy of the lowest spin-triplet state (13B1 state) of halogen-substituted methylenes (CHF, CHCl, CF2, CFCl, and CCl2). Note that in the precedent paper we reported the direct calculation of the vertical excitation energies of CF2 and CCl2 molecules using the BPDE algorithm.11
The results of the N-qubit QPDE simulations are plotted in Figure 6. We observed a strong system dependence of the Trotter–Suzuki decomposition errors. In CHF, CHCl, and CCl2 molecules, the N-qubit QPDE simulations with three different t/M values yielded the same energy difference, and the calculated energy differences agree with the CAS-CI values with less than 0.01 eV of deviation. In contrast, the Trotter–Suzuki decomposition errors are significant for CF2 and CFCl molecules. For example, the deviations of the excitation energies obtained from the N-qubit QPDE from the CAS-CI values in CF2 are 0.056, 0.240, and 0.357 eV for t/M = 0.50, 1.00, and 1.25, respectively. However, by adopting the AEM to mitigate the Trotter–Suzuki decomposition error, the departure of the excitation energy from the CAS-CI value becomes 0.002 eV. The deviations of the ΔEQPDE (AEM) – ΔECAS–CI of CHF, CHCl, CFCl, and CCl2 were calculated to be 0.0000, −0.0075, −0.0096, and −0.0075 eV, respectively. These results also illustrate the importance of the AEM in accurately predicting excitation energies using the N-qubit QPDE algorithm.
Figure 6.

N-qubit QPDE simulation results of the vertical lowest-triplet excitation energies of halogen-substituted methylenes with different time lengths of the single Trotter step t/M. (a) Excitation energy. (b) Differences between the excitation energies from the quantum circuit simulations and those from the CAS-CI/6-31G* calculations. AEM stands for the energy difference obtained by applying algorithmic error mitigation.
To check the dependence of the evolution time length t on the accuracy of the calculated vertical excitation energies, we also carried out N-qubit QPDE simulations with t = 5 instead of t = 10. The results are shown in Figure S8 in the Supporting Information. The calculated ΔEQPDE (AEM) – ΔECAS–CI values are 0.0000, −0.0075, 0.0259, 0.0141, and 0.0117 eV for CHF, CHCl, CF2, CFCl, and CCl2, respectively. Interestingly, when the Trotter–Suzuki decomposition error is small, as in CHF and CHCl, using a shorter evolution time does not affect the calculated excitation energies. However, when the Trotter–Suzuki decomposition error becomes significant, as in CF2, CFCl, and CCl2, the error in the ΔEQPDE (AEM) also becomes large. We expect that the rounding error on the phase value for each simulation will increase with a shorter evolution time, which will affect the performance of the AEM.
4.4. Vertical Excitation Energies of Formaldehyde
The two examples above deal with the energy difference between the lowest singlet and the lowest triplet states. Here, we focus on the vertical excitation energies of the spin-singlet excited states of formaldehyde (HCHO). We have calculated the excitation energies of three low-lying states: the 11A2, the 11B1, and the 21A1 states. As discussed in the Computational Conditions section, these excited states can be approximated by the spin symmetry-adapted (2b2 → 2b1), (5a1 → 2b1), and (1b1 → 2b1) one-electron excitations, respectively, from the |ΦHF⟩ state. Note that direct calculations of the excitation energies of these states have been reported by us using the BPDE algorithm.11 The results are summarized in Figure 7. Again, the Trotter–Suzuki decomposition causes systematic error in the excitation energies, but the error can be efficiently removed by applying the AEM. The calculated excitation energies and those obtained from the BPDE simulations11 are listed in Table 1. Importantly, in all of the excited states under study, the excitation energies obtained from the N-qubit QPDE in conjunction with the AEM agreed with the CAS-CI values with less than 0.006 eV = 0.138 kcal mol–1 of deviation, which is smaller than that of the ΔEBPDE values listed in Table 1. Note that the BPDE simulations11 were carried out using t/M = 0.50. The excitation energies calculated using the N-qubit QPDE and the BPDE methods with the same t/M = 0.50 value are very close to each other. The differences in the excitation energies between the two calculations are mainly due to the shot noise in the BPDE simulations and the nonprojective nature of the BPDE algorithm.
Figure 7.

N-qubit QPDE simulation results of the vertical excitation energies of formaldehyde with different time lengths of the single Trotter step t/M. AEM stands for the excitation energies obtained by applying the algorithmic error mitigation, and dotted horizontal lines indicate the CAS-CI excitation energies.
Table 1. Vertical Excitation Energies of Formaldehyde Calculated by Using the N-qubit QPDE and the BPDE Algorithms and at the CAS-CI Level of Theory.
| state | ΔEQPDE/eV |
ΔEBPDE/eVb | ΔECAS–CI/eV | |||
|---|---|---|---|---|---|---|
| t/M = 1.25 | t/M = 1.00 | t/M = 0.50 | AEMa | |||
| 11A2 | 4.942 | 5.092 | 5.293 | 5.360 | 5.297 | 5.359 |
| 11B1 | 10.135 | 10.268 | 10.469 | 10.530 | 10.466 | 10.525 |
| 21A1 | 11.053 | 11.270 | 11.588 | 11.686 | 11.603 | 11.692 |
The energy difference obtained by applying the algorithmic error mitigation.
Ref (11).
5. Conclusions
In this work, we developed a quantum phase difference estimation algorithm with Na of ancillary qubits for the direct calculations of energy differences on a quantum computer. Although the number of ancillary qubits required to run the algorithm is larger than the previously proposed Bayesian inference-based implementations,11–14 the proposed approach is based on the projective measurement, and therefore it is able to calculate the difference of energy eigenvalues of two electronic states with the approximated wave functions as inputs. The quality of the approximated wave functions only affects the success probability of the calculation, and the calculated energy difference value is independent of the input wave functions. The calculated energy differences show systematic errors mainly caused by the Trotter–Suzuki decomposition. We demonstrated that the error is effectively reduced by applying the algorithmic error mitigation technique. For all the molecules being studied, the error-mitigated energy difference agreed to the full-CI or CAS-CI reference value with less than 1 kcal mol–1 of deviations. Since sophisticated wave function preparation methods such as an adiabatic state preparation require a deep quantum circuit, the single-shot protocol developed in this work is suitable to connect with such approaches. The N-qubit QPDE method with the input wave functions generated by using ASP is in progress and will be discussed in the forthcoming paper.
Acknowledgments
This work was supported by the Center of Innovations for Sustainable Quantum AI (grant no. JPMJPF2221) from JST, Japan; Quantum Leap Flagship Program (JPMXS0120319794) from the MEXT, Japan; and Grants-in-Aid for Scientific Research C (21K03407) and for Transformative Research Area B (23H03819) from JSPS, Japan. Partial support by the PRESTO project “Quantum Software” (JPMJPR1914) from JST, Japan, is also acknowledged.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.3c00784.
Cartesian coordinates and CAS-CI active spaces of halogen-substituted methylenes and formaldehyde, controlled-Pr gates used for the excitation energy calculations of formaldehyde, and N-qubit QPDE simulation results of the vertical excitation energies of halogen-substituted methylenes with the evolution time length t = 5 (PDF)
The author declares no competing financial interest.
Supplementary Material
References
- Dirac P. A. M. Quantum mechanics of many-electron systems. Proc. R. Soc. London, Ser. A 1929, 123, 714–733. 10.1098/rspa.1929.0094. [DOI] [Google Scholar]
- Aspuru-Guzik A.; Dutoi A. D.; Love P. J.; Head-Gordon M. Simulated quantum computation of molecular energies. Science 2005, 309, 1704–1707. 10.1126/science.1113479. [DOI] [PubMed] [Google Scholar]
- Kitaev A. Y.Quantum measurements and the Abelian stabilizer problem. arXiv:quant-ph/9511026, 1995. 10.48550/arXiv.quant-ph/9511026. [DOI]
- Abrams D. S.; Lloyd S. Simulation of many-body fermi systems on a universal quantum computer. Phys. Rev. Lett. 1997, 79, 2586–2589. 10.1103/PhysRevLett.79.2586. [DOI] [Google Scholar]
- Abrams D. S.; Lloyd S. Quantum algorithm providing exponential speed increase for finding eigenvalues and eigenvectors. Phys. Rev. Lett. 1999, 83, 5162–5165. 10.1103/PhysRevLett.83.5162. [DOI] [Google Scholar]
- Lee S.; Lee J.; Zhai H.; Tong Y.; Dalzell A. M.; Kumar A.; Helms P.; Gray J.; Cui Z.-H.; Liu W.; Kastoryano M.; Babbush R.; Preskill J.; Reichman D. R.; Campbell E. T.; Valeev E. F.; Lin L.; Chan G. K.-L. Evaluating the evidence for exponential quantum advantage in ground-state quantum chemistry. Nat. Commun. 2023, 14, 1952. 10.1038/s41467-023-37587-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuzaki Y.; Hakoshima H.; Sugisaki K.; Seki Y.; Kawabata S. Direct estimation of the energy gap between the ground state and excited state with quantum annealing. Jpn. J. Appl. Phys. 2021, 60, SBBI02. 10.35848/1347-4065/abdf20. [DOI] [Google Scholar]
- Yang Y.; Li Y.; Xu X.; Yuan X.. A resource-efficient quantum-classical hybrid algorithm for energy gap evaluation. 2023, arXiv:2305.07382. [Google Scholar]
- Russo A. E.; Rudinger K. M.; Morrison B. C. A.; Baczewski A. D. Evaluating energy differences on a quantum computer with robust phase estimation. Phys. Rev. Lett. 2021, 126, 210501. 10.1103/PhysRevLett.126.210501. [DOI] [PubMed] [Google Scholar]
- Sugisaki K.; Toyota K.; Sato K.; Shiomi D.; Takui T. A quantum algorithm for spin chemistry: a Bayesian exchange coupling parameter calculator with broken-symmetry wave functions. Chem. Sci. 2021, 12, 2121–2132. 10.1039/D0SC04847J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugisaki K.; Sakai C.; Toyota K.; Sato K.; Shiomi D.; Takui T. Bayesian phase difference estimation: a general quantum algorithm for the direct calculation of energy gaps. Phys. Chem. Chem. Phys. 2021, 23, 20152–20162. 10.1039/D1CP03156B. [DOI] [PubMed] [Google Scholar]
- Sugisaki K.; Sakai C.; Toyota K.; Sato K.; Shiomi D.; Takui T. Quantum algorithm for full configuration interaction calculations without controlled time evolutions. J. Phys. Chem. Lett. 2021, 12, 11085–11089. 10.1021/acs.jpclett.1c03214. [DOI] [PubMed] [Google Scholar]
- Sugisaki K.; Wakimoto H.; Toyota K.; Sato K.; Shiomi D.; Takui T. Quantum algorithm for numerical energy gradient calculations at the full configuration interaction level of theory. J. Phys. Chem. Lett. 2022, 13, 11105–11111. 10.1021/acs.jpclett.2c02737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugisaki K.; Prasannaa V. S.; Ohshima S.; Katagiri T.; Mochizuki Y.; Sahoo B. K.; Das B. P. Bayesian phase difference estimation algorithm for direct calculation of fine structure splitting: accelerated simulation of relativistic and quantum many-body effects. Electron. Struct. 2023, 5, 035006. 10.1088/2516-1075/acf909. [DOI] [Google Scholar]
- O’Brien T. E.; Tarasinski B.; Terhal B. M. Quantum phase estimation of multiple eigenvalues for small-scale (noisy) experiments. New J. Phys. 2019, 21, 023022. 10.1088/1367-2630/aafb8e. [DOI] [Google Scholar]
- Gebhart V.; Smerzi A.; Pezzè L. Bayesian quantum multiphase estimation algorithm. Phys. Rev. Appl. 2021, 16, 014035. 10.1103/PhysRevApplied.16.014035. [DOI] [Google Scholar]
- Ding Z.; Lin L. Simultaneous estimation of multiple eigenvalues with short-depth quantum circuit on early fault-tolerant quantum computers. Quantum 2023, 7, 1136. 10.22331/q-2023-10-11-1136. [DOI] [Google Scholar]
- Wiebe N.; Granade C. Efficient Bayesian phase estimation. Phys. Rev. Lett. 2016, 117, 010503. 10.1103/PhysRevLett.117.010503. [DOI] [PubMed] [Google Scholar]
- Paesani S.; Gentile A. A.; Santagati R.; Wang J.; Wiebe N.; Tew D. P.; O’Brien J. L.; Thompson M. G. Experimental Bayesian quantum phase estimation on a silicon photonic chip. Phys. Rev. Lett. 2017, 118, 100503. 10.1103/PhysRevLett.118.100503. [DOI] [PubMed] [Google Scholar]
- Yamamoto K.; Duffield S.; Kikuchi Y.; Muñoz Ramo D.. Demonstrating Bayesian quantum phase estimation with quantum error detection. 2023, arXiv:2306.16608. [Google Scholar]
- Endo S.; Zhao Q.; Li Y.; Benjamin S.; Yuan X. Mitigating algorithmic errors in a Hamiltonian simulation. Phys. Rev. A 2019, 99, 012334. 10.1103/PhysRevA.99.012334. [DOI] [Google Scholar]
- Jordan P.; Wigner E. Über das Paulische äquivalenzverbot. Z. Phys. 1928, 47, 631–651. 10.1007/BF01331938. [DOI] [Google Scholar]
- Seeley J. T.; Richard M. J.; Love P. J. The Bravyi–Kitaev transformation for quantum computation of electronic structure. J. Chem. Phys. 2012, 137, 224109. 10.1063/1.4768229. [DOI] [PubMed] [Google Scholar]
- Veis L.; Pittner J. Adiabatic state preparation of methylene. J. Chem. Phys. 2014, 140, 214111. 10.1063/1.4880755. [DOI] [PubMed] [Google Scholar]
- Kremenetski V.; Mejuto-Zaera C.; Cotton S. J.; Tubman N. M. Simulation of adiabatic quantum computing for molecular ground state. J. Chem. Phys. 2021, 155, 234106. 10.1063/5.0060124. [DOI] [PubMed] [Google Scholar]
- Sugisaki K.; Toyota K.; Sato K.; Shiomi D.; Takui T. Adiabatic state preparation of correlated wave functions with nonlinear scheduling functions and broken-symmetry wave functions. Commun. Chem. 2022, 5, 84. 10.1038/s42004-022-00701-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen M. A.; Chuang I. L.. Quantum Computation and Quantum Information, 10th Anniversary ed.; Cambridge University Press, 2010. [Google Scholar]
- Barca G. M. J.; Bertoni C.; Carrington L.; Datta D.; De Silva N.; Deustua J. E.; Fedorov D. G.; Gour J. R.; Gunina A. O.; Guidez E.; Harville T.; Irle S.; Ivanic J.; Kowalski K.; Leang S. S.; Li H.; Li W.; Lutz J. J.; Magoulas I.; Mato J.; Mironov V.; Nakata H.; Pham B. Q.; Piecuch P.; Poole D.; Pruitt S. R.; Rendell A. P.; Roskop L. B.; Ruedenberg K.; Sattasathuchana T.; Schmidt M. W.; Shen J.; Slipchenko L.; Sosonkina M.; Sundriyal V.; Tiwari A.; Galvez Vallejo J. L.; Westheimer B.; Wloch M.; Xu P.; Zahariev F.; Gordon M. S. Recent developments in the general atomic and molecular electronic structure system. J. Chem. Phys. 2020, 152, 154102. 10.1063/5.0005188. [DOI] [PubMed] [Google Scholar]
- McClean J. R.; Rubin N. C.; Sung K. J.; Kivlichan I. D.; Bonet-Monroig X.; Cao Y.; Dai C.; Fried E. S.; Gidney C.; Gimby B.; Gokhale P.; Häner T.; Hardikar T.; Havlíček V.; Higgott O.; Huang C.; Izaac J.; Jiang Z.; Liu X.; McArdle S.; Neeley M.; O’Brien T.; O’Gorman B.; Ozfidan I.; Radin M. D.; Romero J.; Sawaya N. P. D.; Senjean B.; Setia K.; Sim S.; Steiger D. S.; Steudtner M.; Sun Q.; Sun W.; Wang D.; Zhang F.; Babbush R. OpenFermion: the electronic structure package for quantum computers. Quantum Sci. Technol. 2020, 5, 034014. 10.1088/2058-9565/ab8ebc. [DOI] [Google Scholar]
- Cirq Developers , Cirq, (v1.1.0); Zenodo, 2022. 10.5281/zenodo.7465577. [DOI]
- Trotter H. F. On the product of semi-groups of operators. Proc. Am. Math. Soc. 1959, 10, 545–551. 10.1090/S0002-9939-1959-0108732-6. [DOI] [Google Scholar]
- Suzuki M. Relationship between d-dimensional quantal spin systems and (d + 1)-dimensional Ising systems: equivalence, critical exponents and systematic approximants of the partition function and spin correlations. Prog. Theor. Phys. 1976, 56, 1454–1469. 10.1143/PTP.56.1454. [DOI] [Google Scholar]
- Yung M.-H.; Whitfield J. D.; Boixo S.; Tempel D. G.; Aspuru-Guzik A.. In Quantum Information and Computation for Chemistry, Advances in Chemical Physics; Kais S., Rice S. A., Dinner A. A., Eds.; Wiley: NJ, 2014; Vol. 154, pp 67–106. [Google Scholar]
- Cao Y.; Romero J.; Olson J. P.; Degroote M.; Johnson P. D.; Kieferová M.; Kivlichan I. D.; Menke T.; Peropadre B.; Sawaya N. P. D.; Sim S.; Veis L.; Aspuru-Guzik A. Quantum chemistry in the age of quantum computing. Chem. Rev. 2019, 119, 10856–10915. 10.1021/acs.chemrev.8b00803. [DOI] [PubMed] [Google Scholar]
- Tranter A.; Love P. J.; Mintert F.; Coveney P. V. A comparison of the Bravyi–Kitaev and Jordan–Wigner transformations for the quantum simulation of quantum chemistry. J. Chem. Theory Comput. 2018, 14, 5617–5630. 10.1021/acs.jctc.8b00450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tranter A.; Love P. J.; Mintert F.; Wiebe N.; Coveney P. V. Ordering of Trotterization: Impact on errors in quantum simulation of electronic structure. Entropy 2019, 21, 1218. 10.3390/e21121218. [DOI] [Google Scholar]
- Sugisaki K.; Nakazawa S.; Toyota K.; Sato K.; Shiomi D.; Takui T. Quantum chemistry on quantum computers: a method for preparation of multiconfigurational wave functions on quantum computers without performing post-Hartree–Fock calculations. ACS Cent. Sci. 2019, 5, 167–175. 10.1021/acscentsci.8b00788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doehnert D.; Koutecky J. Occupation numbers of natural orbitals as a criterion for biradical character. Different kinds of biradicals. J. Am. Chem. Soc. 1980, 102, 1789–1796. 10.1021/ja00526a005. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Keith T.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 09, Revision B.01, 2010.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.





